双筋矩形截面梁板设计案例(精)

双筋矩形截面适用范围
双筋矩形截面的适用范围主要包括以下两种情况：
1. 当截面尺寸和材料强度受建筑使用和施工条件（或整个工程）限制而不能增加，而计算又不能满足适筋截面条件时，采用双筋截面。

2. 当梁的同一截面有承受异号弯矩的作用时，例如连续梁中的跨中截面，这种情况需要采用双筋截面。

综上所述，双筋矩形截面的适用范围主要涵盖了各种原因导致的结构安全必须由增加受拉和受压钢筋才能满足要求的情况。

请注意，如果满足不了使用要求或具体情况较为复杂，建议咨询专业人士获取帮助。

' s

M —— 外荷载所产生的弯矩设计值
M u —— 截面自身的抗弯承载力
T
—— 钢筋所受拉力
f y —— 钢筋抗拉强度设计值（屈服强度）
As —— 受拉钢筋截面面积
fc —— 砼的轴心抗压强度设计值。
b —— 梁截面宽
x
' s
—— 砼受压区高度
f y' —— 钢筋抗压强度设计值（屈服强度）
A —— 受压钢筋截面面积
3 22
2
25 250
例5、同上例，但事先给定压筋2 25 (As´ =982mm2)， 求As。
x h0 h0
2
M f y´As (h´ a´ ) 0 s 2 f cm b
解：一、求x
219 106 310 982 (440 35) 440 4402 2 11 200 b h0 0.544 440 239(mm) 440 326 114(m m) 2as´ 2 35 70(mm)
2
11 200 440 0.544 (1 0.5 0.544) 168.7(kN m) M 219(kN m)
2
故应用双筋截面
二、求As´和As
M ´ s max bh0 f cm ´ As f y (h0 a s )
´
2
219 10 6 0.396 200 440 2 11 310 (440 35) 401(mm 2 )
' y ' s
1 fc b
2、求 若
' s
Mu
x ' ' ' f y As h0 as 2

因弯矩较大，初估钢筋布置为两层，取a=75mm，则h0=h －as=500－75=425mm。
s
KM f c bh 0
2

1 . 25 190 . 65 10 9 . 6 250 425
2
6
0 . 550 s max 0 . 358
a
h0
A s
As a b
x<2as'时双筋截面计算图形
三、公式应用
设计类型Ⅰ
（一）截面设计
已知：弯矩设计值M，截面尺寸b，h，材料强度fy、fc
未知：x，As ´， As （1）判断是否应采用双筋截面进行设计 根据弯矩设计值M及截面宽度b的大小，估计受拉钢筋布 置的层数并选定a，计算出h0和αs值，并与αsb值进行比较。 若αs≤αsb，应采用单筋截面进行设计；否则应采用双筋截 面进行设计。
截面设计时，可偏安全地取受压纵筋合力点Ds与受压混凝土合
力点Ds重合，如图2-24所示。以受压钢筋合力点为力矩中心，可得： KM f y As ( h 0 a s )
若计算中不考虑受压钢筋的作用，则条件x≥2as'即可取消。
双筋截面承受的弯矩较大，相应的受拉钢筋配置较多，一般均能满 足最小配筋率的要求，无需验算ρmin的条件。
x h 0 0 . 1 78 425 76 mm 2 a s 2 45 90 mm
As KM f y ( h0 a s ) 1 . 25 190 . 65 10 300 ( 425 45 )
6
2090 mm
2
（3）选配钢筋，绘制配筋图 选受拉钢筋为3 25＋2 20（As=2101 mm2），配筋如图所示。

双筋截面设计步骤
已知 M,b,h,fc,fy,fy’,As’
M f y ' As ' ( h0 s ' ) 2 x h0 h0 2 f b 1 c
2as ' x b h0
Ｙ
As
1 f cbx
fy
As
【例题4】
已知：在荷载设计值作用下的 M=230KN.m；砼等级C20；钢 筋HRB335 ,截面尺寸200×500mm ,在受压区已配置了3φ25， AS’=1473mm2 求受拉钢筋 h = 500- 65 = 435mm
【例题4】
已知：在荷载设计值作用下的 M=230KN.m；砼等级C20；钢 筋HRB335 ,截面尺寸200×500mm 求受拉钢筋
5. 计算As
AS
1 f cbbh0 ASf y
fy 9.6 200 0.55 435 718.39 300 AS 300 As 2249 .59m m2
b ,
x 2a s or s h0 x 2 a s
【例题4】
已知：在荷载设计值作用下的 M=230KN.m；砼等级C20；钢 筋HRB335 ,截面尺寸200×500mm 求受拉钢筋
1.查表得有关数据 ２.确定 h0
C 20 : f c 9 .6 N / mm 2； II 级 钢 筋 ：f y 300 N / mm 2
x b h0
说明As ' 太小，按As ' 未知，重新计算 As ' 和As
1 f cbx
fy
As
【例题5】
已知：某钢筋砼梁，采用砼等级C35；钢筋HRB400 ,截面尺 寸300×600mm ,在受压区已配置了2φ16，受拉钢筋4φ25，求梁 截面所能承受的弯矩设计值Mu

（2）受拉钢筋为5 25时（As=2454mm2） a=c＋d＋e/2=35＋25＋30/2=75mm h0=500－75=425mm
x f y As f yAs f cb 300(2454 1140 ) 205mm 9.6 200
＞0.85ξbh0=0.85×0.55×425=199mm 此梁为超筋截面，代入式（2-9）计算承载力 KM≤αsmax fcbh02+ fy'As'（h0-a'） =0.358×9.6×200×4252+300×1140×(425-45) =254.11kN· m M =254.11/1.25=203.23kN· m＞195kN· m 该构件的正截面安全。
双筋矩 形截面 梁正截 面承载 力计算 简图
（三）适用条件
（1）x≤0.85ξbh0或ξ≤0.85ξb；避免发生超筋破坏，保证受拉钢筋应 力达到抗拉强度设计值fy。
（2）x≥2as'；保证受压钢筋应力达到抗压强度设计值fy′。
若x＜2as'，截面破坏由纵向受拉钢筋应力达到fy引起，此时， 纵向受压钢筋应力尚未达到fy'。
0.85 f cb b h0 f y As
（3）选配钢筋，绘制配筋图 根据钢筋表，选出符合构造规定的钢筋直径、间距 和根数，绘制正截面配筋图。
设计类型II 已知：弯矩设计值M，截面尺寸b、h，钢筋级别，砼强度 等级，受压钢筋截面面积As′。
求：受拉钢筋截面面积As。
1.计算截面抵抗矩系数α
受拉钢筋为5 25（As=2454mm2）， 截面配筋如下图所示。
【案例2-8】已知同例2-7，若受压区已采用两种情况配置钢筋： ①配置3 18钢筋（As'=763mm2）；②配置3 25钢筋 （As'=1473mm2），试分别计算两种情况受拉钢筋面积As。

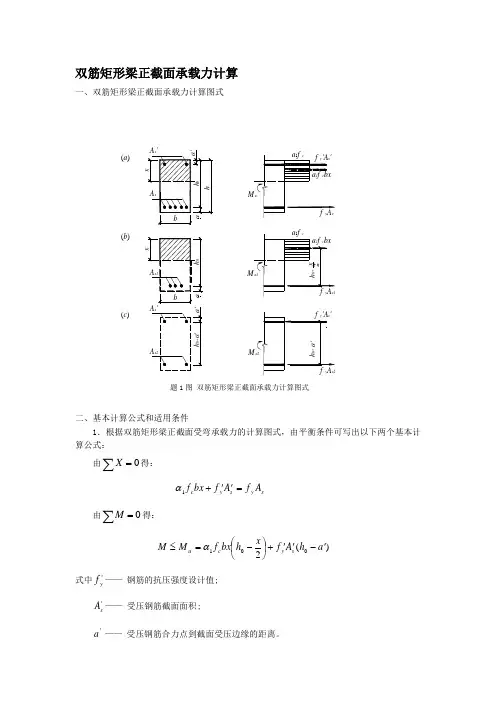
双筋矩形梁正截面承载力计算一、双筋矩形梁正截面承载力计算图式二、基本计算公式和适用条件1．根据双筋矩形梁正截面受弯承载力的计算图式，由平衡条件可写出以下两个基本计算公式：由∑=0X 得：s y s y c A f A f bx f =''+1α由∑=0M 得：)(2001a h A f x h bx f M M s y c u '-''+⎪⎭⎫ ⎝⎛-=≤α 式中'y f —— 钢筋的抗压强度设计值;'s A —— 受压钢筋截面面积; 'a —— 受压钢筋合力点到截面受压边缘的距离。

其它符号意义同前。

2．适用条件应用式以上公式时必须满足下列适用条件： （1）0h x b ξ≤（2）'2a x ≥如果不能满足(2)的要求，即'2a x <时，可近似取'2a x =，这时受压钢筋的合力将与受压区混凝土压应力的合力相重合，如对受压钢筋合力点取矩，即可得到正截面受弯承载力的计算公式为：)(0a h A f M M s y u '-=≤ 当b ξξ≤的条件未能满足时，原则上仍以增大截面尺寸或提高混凝土强度等级为好。

只有在这两种措施都受到限制时，才可考虑用增大受压钢筋用量的办法来减小ξ。

三、计算步骤（一）截面选择（设计题）设计双筋矩形梁截面时，s A 总是未知量，而's A 则可能有未知或已知这两种不同情况。

1．已知M 、b 、h 和材料强度等级，计算所需s A 和'sA （1）基本数据：c f ，y f 及'y f ，1α, 1β，b ξ（2）验算是否需用双筋截面由于梁承担的弯矩相对较大，截面相对较小，估计受拉钢筋较多，需布置两排，故取mm a 60=，a h h -=0。

单筋矩形截面所能承担的最大弯矩为：M bh f M b b c u <-=)5.01(201max 1ξξα，说明需用双筋截面。

≥ρmin′bh0
As
0.85 fcbbh0
fy
f yAs
（3）选配钢筋，绘制配筋图
根据钢筋表，选出符合构造规定的钢筋直径、间距
和根数，绘制正截面配筋图。
设计类型II
已知：弯矩设计值M，截面尺寸b、h，钢筋级别，砼强度
等级，受压钢筋截面面积As′。 求：受拉钢筋截面面积As。 1.计算截面抵抗矩系数α
s
KM
f yAs (h0 f cbh0 2
as )
2.计算砼受压区相对高度ξ、x，求As
若ξ＞0.85ξb或x＞0.85ξbh0，说明已配置受压钢筋As′的数量
不足，此时应按【设计类型I】的步骤进行计算。
若2as ′≤x≤0.85ξbh0，则
As
fcbh0
fy
f yAs
若x ＜ 2a s′ ，则
配置普通钢筋，对结构抗震有利。
受压钢筋
A s'
As
返回
单筋截面与双筋截面的区别
架立钢筋
受压钢筋
受拉钢筋
受拉钢筋
单筋截面
仅在受拉区配置纵向 受力钢筋的截面。
受压钢筋
A s'
双筋截面
As
在受拉区与受压区都 配置纵向受力钢筋的截
面。
二、基本公式及适用条件
（一）受压钢筋的设计强度 双筋截面只要满足ξ≤0.85ξb，就具有单筋截面适筋梁的破坏 特征。 钢筋和混凝土之间具有粘结力，所以，受压钢筋与周边混凝 土具有相同的压应变，即εs'=εc。当受压边缘混凝土纤维达到极限 压应变时，受压钢筋应力бs'=εs'Es=εc Es。 正常情况下（x≥2as'），取εs'=εc=0.002。бs'=0.002× （1.8×105~2.0×105） =（360~400）N/mm2。 若采用中、低强度钢筋作受压钢筋（≤400 N/mm2），且混凝 土受压区计算高度x≥2as'，构件破坏时受压钢筋应力能达到屈服 强度； 若采用高强度钢筋作为受压钢筋，则其抗压强度设计值不应 大于400 N/mm2。

f y As1 f y As
(h0 as/ ) Mu1 f y As
②受压区混凝土和与其相应的一 部分受拉钢筋承受的弯矩 M u 2
1 fcbx f y As 2
M u 2 1 f c bx (h0 1 x) 2
6
叠加得
M u M u1 M u 2
抗 弯 计 算
②若
说明给定的
太少，应按情况1的步骤重新求 As As
As
③若
x 2a s
不能达到屈服，此时有两种偏安全的近似处理方法： As
说明受压钢筋
16
抗 弯 计 算
a.令 b.令
x 2a s
0 As
。
As
M ) f y ( h0 a s
按单筋矩形截面求
As
∵按a、b计算的 As 均偏安全（大于实际所需的 As ），∴所需的
抗 弯 计 算
应该说明，双筋 矩形截面的用钢 量比单筋截面的
由于某些原因又不能改变； b 承受某种交变荷载的作用（如风载、振动和地 震），使截面上的弯矩改变符号。
多，为节约钢材， 应尽可能地不要
F
A
B
A
B
F
将截面设计成双 筋截面。
在地震作用下门式刚架横梁的内力
3
2破坏特征
（1）双筋截面的适筋梁破坏特点：
' s
As
f y' As' 1 f c b b h0 fy
3068 .4m m2
13
3 选配钢筋 受拉钢筋选8根直径22，As=3041mm2, 受压钢筋选2根直径22, As’=760mm2。 4 验算
抗 弯 计 算

a.若x＞0.85ξbh0，取x=0.85ξbh0，则ξ=0.85ξb、αs=αsmax，此 时，则构件的正截面安全，否则不安全。 KM≤αsmaxfcbh02+ fy'As'（h0-as'） b.若2as'≤x≤0.85ξbh0，此时，则构件的正截面安全，否则不 安全。
KM ≤ f y As (h0
2
2.计算砼受压区相对高度ξ、x，求As
若ξ＞0.85ξb或x＞0.85ξbh0，说明已配置受压钢筋As′的数量 不足，此时应按【设计类型I】的步骤进行计算。
若2as ′≤x≤0.85ξbh0，则
As =
若x ＜ 2a s′ ，则
′ f cbξh0 + f y′ As fy
KM As = ′ f y (h0 as )
（二）基本公式
由截面内力平衡条件得 ∑x =0 ∑M=0 fc b x + fy'As'= fyAs KM≤fcbx（h0-0.5x）+ fy'As'（h0-as '） （2-32） （2-33）
将x=ξh0及αs=ξ（1－0.5ξ）代入上式得： KM ≤ αs f cbh0 + f y′ As′ (h0 双筋矩 形截面 梁正截 面承载 力计算 简图
【案例2-10】
某水电站厂房（3级建筑物）中的简支梁，截面尺寸为200
mm×500 mm。混凝土强度等级为C25，受压钢筋3 22
（As′=1140mm2，as′=45mm），二类环境条件，受拉钢筋采用 6 22配置，承受弯矩设计值为M=195kN· m，试复核此截面是 否安全。
解： 查表得：fy=fy´=300N/mm2，K=1.20， c=35 mm， fc=11.9N/mm2。 （1）受拉钢筋为6 22时（As=2281mm2，as=c＋d＋e/2=35＋22

钢筋与混凝土协同工作
双筋矩形截面中的钢筋和混凝土共同工作，钢筋承受拉力，混凝土 承受压力，共同维持结构的稳定性。
增强结构刚度
双筋矩形截面通过钢筋的布置，增强了结构的刚度，提高了结构的 承载能力和抗震性能。
受力分析方法
解析法
实验法
通过力学原理和数学公式，对双筋矩 形截面的受力情况进行解析，得出各 部分的应力分布和承载能力。
双筋矩形截面
目录
• 双筋矩形截面的定义 • 双筋矩形截面的受力分析 • 双筋矩形截面的设计 • 双筋矩形截面的施工 • 双筋矩形截面的优化建议
双筋矩形截面的定
01
义
定义
01
双筋矩形截面是指在矩形截面的 梁或柱中配置两根纵向受力钢筋 的截面形式。
02
它是一种常见的混凝土结构形式 ，广泛应用于桥梁、建筑和工业 厂房等建筑结构中。
通过合理的截面设计，提高截面的承载能力和稳定性。
详细描述
优化截面的尺寸和形状，以实现最佳的承载能力和稳定性。例如，增加腹板的高度和厚度可以提高截面的抗弯和 抗剪切能力。合理布置钢筋，包括数量、直径和间距，以确保截面在各种受力状态下都能充分发挥其承载能力。
施工优化
总结词
通过合理的施工方法和技术，确保截面的施工质量，提高其实际承载能力。
双筋矩形截面的优
05
化建议
材料优化
总结词
选择高强度、高质量的材料，以提高截面的承载能力和耐久 性。
详细描述
使用高强度钢材，如高碳钢或合金钢，可以显著提高截面的 承载能力，同时减少截面的尺寸和重量。选择优质的材料， 如不锈钢或耐腐蚀材料，可以提高截面的耐久性，减少腐蚀 和疲劳损伤。
设计优化
总结词
设计步骤

其含义为受压钢筋位置不低于矩形受压应力图形的重心。当不满足此项规定时， 则表明受压钢筋的位置离中和轴太近，受压钢筋的应变 太小，以致其应力达 不到抗压强度设计值 。 (3) 双筋截面一般不必验算ρmin，因为受拉钢筋面积较大。
第6页/共23页
3.5 双筋矩形截面受弯承载力
3.5.4 基本公式的应用 情况1：已知：M, b×h, fc, fy, fy/ 求：As, As/
求：验算此截面是否安全?
第19页/共23页
3.5 双筋矩形截面受弯承载力
3.5.6 算例
解：fc=14.3N/mm2，fy=fy’=300N/mm2。由表知，混凝土保护
层最小厚度为35mm，故
mm，h0=400-47.5=352.5mm
由式
代入式
注意，在混凝土结构设计中，凡是正截面承载力复核题，都必须求出混凝土受
图3-31 当梁宽大于400mm且一层内的受压纵筋多于3根时，或 梁宽不大于400mm但一层内的受压纵筋多于4根时，应设复 合箍筋。
第2页/共23页
3.5 双筋矩形截面受弯承载力
3.5.2 基本公式
双筋矩形截面受弯构件正截面受弯的截面计算图形如图所示。
由力的平衡条件可得：
图3-32
第3页/共23页
配置受压钢筋后为防止纵向受压钢筋可能发生纵向弯曲压屈而向外凸出引起保护层剥落甚至使受压混凝土过早发生脆性破坏应按规范规定箍筋应做成封闭式箍筋直径不小于受压钢筋最大直径的14且应满足一定的要求混凝土规范10210条
3.5 双筋矩形截面受弯承载力
配置受压钢筋后，为防止纵向受压钢筋可能发生纵向弯曲 (压屈)而向外凸出，引起保护层剥落甚至使受压混凝土过早发 生脆性破坏，应按规范规定，箍筋应做成封闭式，箍筋直径不 小于受压钢筋最大直径的1/4，且应满足一定的要求（混凝土规 范10.2.10条）。规范部分要求见图3-31。

双筋矩形截面梁正截面受弯承载力计算公式的适用条件梁是建筑结构中常见的构件，承担着主要的受力任务。

在设计和施工中，对梁的承载能力进行准确的计算和评估至关重要。

而对于双筋矩形截面梁来说，其正截面受弯承载力计算公式的适用条件是关键的问题，本文将在此探讨。

一、双筋矩形截面梁简介双筋矩形截面梁是一种常见的混凝土梁截面形式，其在横截面上呈矩形状，同时设有两根钢筋以增强其受拉能力，从而使得梁的承载能力得到提高。

双筋矩形截面梁通常用于大跨度、大荷载的结构中，具有良好的承载性能和变形性能。

二、正截面受弯承载力计算公式正截面受弯承载力是指梁在受到弯矩作用时的承载能力，对于双筋矩形截面梁来说，其正截面受弯承载力计算公式通常可以用以下公式表示：1.```N_u = \phi \times \left( \alpha_1 \times A_s \times f_y +\alpha_2 \times A'_s \times f_y' \right)```其中，N_u为受弯承载力，单位为kN；\phi为折减系数，通常取为0.9；\alpha_1为混凝土应变分布影响系数，通常取为0.85；A_s为受拉钢筋面积，单位为mm^2；f_y为钢筋的屈服强度，单位为MPa；\alpha_2为受拉钢筋的应变分布影响系数，取为1.0；A'_s为受拉箍筋面积，单位为mm^2；f_y'为箍筋的屈服强度，单位为MPa。

2.```M_u = \phi \times \left( \alpha_1 \times A_s \times f_y \times d - \alpha_2 \times A'_s \times f_y' \times d' \right)```其中，M_u为弯矩抵抗矩，单位为kN·m；\phi为折减系数，取为0.9；\alpha_1为混凝土应变分布影响系数，取为0.85；A_s为受拉钢筋面积，单位为mm^2；f_y为钢筋的屈服强度，单位为MPa；d为受拉钢筋与受压区边缘的距离，单位为mm；\alpha_2为受拉钢筋的应变分布影响系数，取为1.0；A'_s为受拉箍筋面积，单位为mm^2；f_y'为箍筋的屈服强度，单位为MPa；d'为箍筋与受压区边缘的距离，单位为mm。

M2＜0，表明由混凝土和As所负担的弯矩设计值为负，
按构造进行配筋即可。
As=ρminbh=0.2%×200×450=180mm2 从这个例题可以看出，当弯矩设计值取 ①M＞
M单 筋 max ；② M压 筋 ≤M ≤ M单 筋 max；③ M ＜M 压 筋 三 种 情 况时按单筋矩形截面梁求得的As值均大于公式（3）求 得的As值。
旨在提高教学质量并锻炼学生思考、解决工程问题的能力。
关键词：双筋梁；受压钢筋；屈服；截面设计；单筋梁
中图分类号：TU375
文献标志码：A
文章编号：1674-9324（2019）46-0186-03
混凝土结构教学过程中，计算双筋矩形截面梁时
会遇到受压钢筋不屈服的情况，即出现x＜2a忆s的情
况，则按受压钢筋屈服建立的计算公式将不再适用，
称为纵向受压钢筋[1-4]。双筋矩形截面受弯构件极限承
载力的计算公式为式（1）和（2）：
α1fcbx+f忆yA忆s=fyAs
蓸 蔀 M≤α1fcbx
h0-
x 2
+f忆yA忆（s h0-a忆s）
（1） （2）
公式（1）和（2）的适用条件为：
①为了防止构件发生超筋破坏，应满足ξ≤ξb； ②为了保证受压钢筋在构件破坏时达到屈服，应
单筋截面所负担的弯矩为：
M2=M-M压筋=180-115.3=64.7kN·m
αs2=
M2 α1fcbh20
=
64.7×106 1.0×14.3×200×3802
=0.157
＜αsb=0.384
ξ=1- 姨1-2αs2 =1-姨1-2×0.157 =0.171
x=ξh0=0.171×380=65＜2a忆s=80mm

fy¢As¢ fyAs2 M¢fy¢As¢(h0a¢)
纯钢筋部分
A s¢
As1
As2
受压钢筋与其余部分受拉钢筋As2组成的“纯钢筋截面” 的受弯承载力与混凝土无关
因此截面破坏形态不受As2配筋量的影响，理论上这部分 配筋可以很大，如形成钢骨混凝土构件。
本文档所提供的信息仅供参考之用，不能作为科学依据，请勿模仿。文档如有不 当之处，请联系本人或网站删除。
１、已知：b、h、a、a’、As、As’ 、fy、 fy’、fc
求：Mu≥M 未知数：受压区高度 x 和受弯承载力Mu两个未知数，有唯一解。
afcbx fy¢As¢fyAs MMua1fcb(xh02 x)fy¢As¢(h0a¢)
xbh0 x2as'
当Mu≥M时，满足安全要求
本文档所提供的信息仅供参考之用，不能作为科学依据，请勿模仿。文档如有不
３、基本公式
平衡方程表示的基本公式如下：
afcbxfy¢As¢ fyAs Mafcb(xh02x)fy¢As¢(h0a¢)
afcbx fy As1
M1

afcbx(h0

x) 2
单筋部分
fy¢As¢ fyAs2 M¢ fy¢As¢(h0 a¢)
纯钢筋部分
本文档所提供的信息仅供参考之用，不能作为科学依据，请勿模仿。文档如有不 当之处，请联系本人或网站删除。
为使受压钢筋的强度能充分发挥，其应变不应小于0.002。
由e平s¢ 截e面cu假(1定xa可n¢)得，0.002ecu=0.0033
x2a¢
本文档所提供的信息仅供参考之用，不能作为科学依据，请勿模仿。文档如有不
二）基本公式 当之处，请联系本人或网站删除。

双 筋 矩 形 截 面受 弯构 件 用 钢 量 较 大 ， 一 种 是 不够 经济 的截 面 配 筋 形 式 ， 在 实 际 工 程 中有 时 而 又不 得不 采用 这种 形 式 ， 国《 我 钢筋 混凝 土 结 构 设
分析 ， 到 了钢 筋 混 凝 土 双 筋 矩 形 截 面 梁 的 截 面 达 尺寸及 配 筋 设 计 与 构 件 经 济 性 较 好 结 合 ， 出 了 得 实用设 计 计算 方法 及 计算公 式 。
Ｋｅ ｗｏ ｄ ｆｅ ｕ ａ ｍｂ ｒ ｐ ｉ ｚ ｄ ｄ ｓｇ ｙ ｒ ｓ： ｘ ｒ ｌｍｅ ｅ ；ｏ ｔｍｉｅ ｅ ｉ ｎ；ｒ ｓｒ ｉ ｅ ａ ｔｒ ｅｎ ｏ ｃ ｍｅ ｔｐ ｒ ｅ ｔ ｇ ｌ ｅ ｔａ ｎ ｄ ｆ ｃｏ ；ｒ ｉｆ ｒ ｅ ｎ现行规范是以经济配筋率作为衡量结构 设计 能满 足承 载力要 求 而 截 面 尺 寸 又 受 到 限 制 或构 件 经 济性 的标准 ， 在 工 程 实 际 中 ， 济 配筋 率 是一 但 经 受 变 号弯 矩作 用 时或 构 件 受 压 区 已 配 置受 压 钢 筋 个 比较 复 杂 的问题 ， 它受 结 构 形 式 、 料 价格 及 施 材
Ａｂ ｔ ａ ｔ Ｕ ｄ ｒｔ ｅ ｃ ｎ ｉ ｏ ｆｓｒ ｃｕ ａ ｅｉｂ ｌ ｙ ｈ ｓ ｐ ｐ ｒ ｍａ ｅ ｓ ｆ ａ ａｙ ｉ ｍｅｈ ｄ ｏ ｏ ｄｔ ｎ ｅ ｔ － ｓｒ ｃ ： ｎ ｅ ｏ ｄｔ ｎ ｏ ｔ ｔ ｒ ｌｒｌ ｉ ｔ ，ｔ ｉ ａ ｅ ｋ ｓ ｕ ｅ ｏ ｎ ｓｓ ｔ ｏ ｆｃ ｎ ｉ ｘ ｒ ｈ ｉ ｕ ａ ｉ ｌ ｉ ｏ ｅ ｍｕ ｉ ｉｈ ｒｍａｈ ｍａ ｉｓ ｃ ｍｂ ｎ ｓｒ ｃａ ｇ ｌ ｒ ｅ ｕ ａ ｍｅ ｅ ｆｒｉ ｆｒ ｅ ｏ ｃ ｅｅｏ ｏ ｂ ｅ ｂ ｒ ｉ ｅｅ ｏ ｍ ｈ ｇ ｅ ｔ ｅ ｔ ， ｏ ｉ ｅ ｔ ｕａ ｘ ｌ ｎ ｃ ｅ ｎ ｌ ｆ ｒ ｍｂ ｒ ｎ ｏｃ ｄ ｃ ｎ ｒ ｔ ｆ ｕ ｌ ａｓｗ ｔ ｔ ｃ － ｏ ｅ ｄ ｈｈ ｎ ｍｉ ｏ ｔ ｃｕ ａ ｌｍｅ ｔ ｎ ｄ ｐ ｏ ｏ ｅ ａｅ， ｅ ｎ ａ ｌ ，ｅ ｏ ｏ ｃ ｄ ｐ ａ ｔ ａ ｐ ｉ ｚ ｄ Ｄ ｓｇ ｔｏ ． ｏ ｃ ｆｓｒ ｔ ｌ ｅｅ ｎ ，ａ ｒ ｐ ｓ ｓ ｓｆ ｄ ｐ ｄ ｅ ｃ ｎ ｍｉ ａ ａ ｒ ｃｉｌ Ｏ ｔ ｅ ｅ ｉｎ Ｍｅｈ ｄ ｕ ｒ ｅ ｂ ｌ ｎ ｃ ｉ ｍ

职业教育水利水电建筑工程专业《水工混凝土结构》例题（双筋矩形截面梁板设计）《水工混凝土结构》项目组2015年3月双筋矩形截面梁板设计——例题【案例7–1】已知某矩形截面简支梁（2级建筑物），b ×h =250mm×500mm ，二类环境条件，计算跨度l 0=6500mm ，在使用期间承受均布荷载标准值g k =18kN/m （包括自重），q k =15kN/m ，混凝土强度等级为C25，钢筋为HRB335级。

计算受力钢筋截面面积（假定截面尺寸、混凝土强度等级因条件限制不能增大或提高）。

解：查表得：f c =11.9N/mm 2，f y =f y ′=300N/mm 2，K =1.20，c =35mm ，ξb =0.550，αsmax =0.358。

（1）确定弯矩设计值MM =（1.05g k +1.20q k ）l 02/8=（1.05×18+1.20×15）×6.52/8=194.88kN ·m（2）验算是否应采用双筋截面因弯矩较大，初估钢筋布置为两层，取a s =75mm ，则h 0=h –a s =500–75=425mm 。

358.0435.04252509.111088.19420.1max s 2620c s =>=⨯⨯⨯⨯==ααbh f KM 属于超筋破坏，应采用双筋截面进行计算。

（3）配筋计算设受压钢筋为一层，取a s '=45mm ；为节约钢筋，充分利用混凝土抗压，取x =0.85ξb h 0，则αs =αsmax ，由公式（2–37）、（2–38）得：)(s0y 20c max s s a h f bh f KM A '-'-='α =364454253004252509.11358.01088.19420.126=-⨯⨯⨯⨯-⨯⨯）（mm 2＞0.2﹪bh 0=0.2﹪×250×425=213 mm 22334300364300425550.02509.1185.085.0ys y 0b c s =⨯+⨯⨯⨯⨯=''+=f A f h b f A ξmm 2（4）选配钢筋并绘制配筋图选受压钢筋为216（A s ′=402mm 2），受拉钢筋为525（A s =2454mm 2），截面配筋如图1所示。

改进的双筋矩形截面梁配筋设计
孙荣书;刘华新;王丹丹;刘宇欣
【期刊名称】《辽宁工业大学学报（自然科学版）》
【年(卷),期】2007(027)003
【摘要】对建筑工程中常见的现浇钢筋混凝土双筋矩形截面梁的配筋设计方法进行改进,考虑了抗震要求的承载力条件和不考虑抗震要求的承载力条件以及纵向受力钢筋最小配筋率等,得出的计算结果既满足构造要求,又避免了配筋结果需反复计算的缺点,使双筋梁的截面配筋设计步骤得到进一步简化.
【总页数】3页(P165-167)
【作者】孙荣书;刘华新;王丹丹;刘宇欣
【作者单位】辽宁工业大学,土木建筑系,辽宁,锦州,121001;辽宁工业大学,土木建筑系,辽宁,锦州,121001;辽宁工业大学,土木建筑系,辽宁,锦州,121001;辽宁工业大学,土木建筑系,辽宁,锦州,121001
【正文语种】中文
【中图分类】TU323.3
【相关文献】
1.单筋和双筋矩形截面梁的相关性分析 [J], 赵守勇;王丰;胡泽友;郭弘琳;王建锋
2.双筋矩形RC梁配筋设计影响因素及变化规律研究 [J], 曹锋; 陈梦霞; 陈志远; 谭镇
3.钢筋混凝土受弯构件双筋矩形截面配筋设计经济计算法 [J],
4.基于C++平台的混凝土梁配筋程序设计——以双筋矩形截面梁正截面抗弯为例
[J], 陈汉阳;刘一哲;张博方;谢丹凤;陈雨霄
5.基于C++平台的混凝土梁配筋程序设计
——以双筋矩形截面梁正截面抗弯为例 [J], 陈汉阳;刘一哲;张博方;谢丹凤;陈雨霄因版权原因，仅展示原文概要，查看原文内容请购买。