双筋矩形截面受弯构件正截面承载力计算

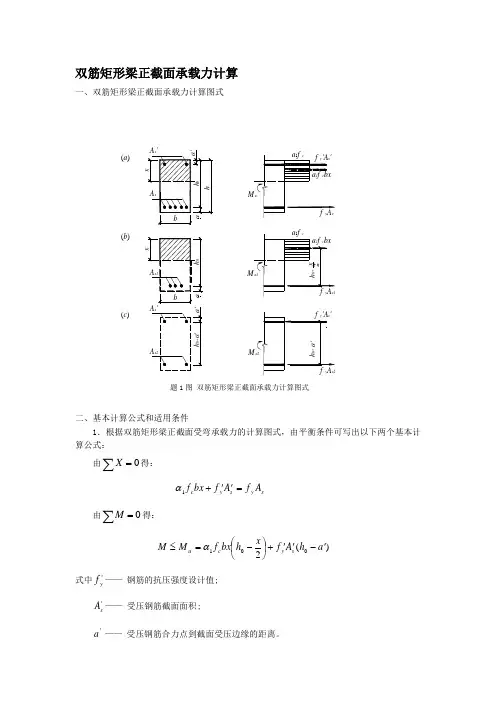
双筋矩形梁正截面承载力计算一、双筋矩形梁正截面承载力计算图式二、基本计算公式和适用条件1．根据双筋矩形梁正截面受弯承载力的计算图式，由平衡条件可写出以下两个基本计算公式：由∑=0X 得：s y s y c A f A f bx f =''+1α由∑=0M 得：)(2001a h A f x h bx f M M s y c u '-''+⎪⎭⎫ ⎝⎛-=≤α 式中'y f —— 钢筋的抗压强度设计值;'s A —— 受压钢筋截面面积; 'a —— 受压钢筋合力点到截面受压边缘的距离。

其它符号意义同前。

2．适用条件应用式以上公式时必须满足下列适用条件： （1）0h x b ξ≤（2）'2a x ≥如果不能满足(2)的要求，即'2a x <时，可近似取'2a x =，这时受压钢筋的合力将与受压区混凝土压应力的合力相重合，如对受压钢筋合力点取矩，即可得到正截面受弯承载力的计算公式为：)(0a h A f M M s y u '-=≤ 当b ξξ≤的条件未能满足时，原则上仍以增大截面尺寸或提高混凝土强度等级为好。

只有在这两种措施都受到限制时，才可考虑用增大受压钢筋用量的办法来减小ξ。

三、计算步骤（一）截面选择（设计题）设计双筋矩形梁截面时，s A 总是未知量，而's A 则可能有未知或已知这两种不同情况。

1．已知M 、b 、h 和材料强度等级，计算所需s A 和'sA （1）基本数据：c f ，y f 及'y f ，1α, 1β，b ξ（2）验算是否需用双筋截面由于梁承担的弯矩相对较大，截面相对较小，估计受拉钢筋较多，需布置两排，故取mm a 60=，a h h -=0。

单筋矩形截面所能承担的最大弯矩为：M bh f M b b c u <-=)5.01(201max 1ξξα，说明需用双筋截面。

二、双筋矩形截面受弯构件正承载力计算（一）计算简图在进行双筋矩形截面受弯构件正截面承载力计算时，计算简图如图3-19所示。

（二）基本公式（1）设计表达式根据图3-19所示的计算简图和内力平衡条件，可列出基本设计计算公式()⎥⎦⎤⎢⎣⎡'-''+⎪⎭⎫ ⎝⎛-=≤a h A f x h bx f M M 0s y 0c d d u 21γγ （3-14） s y s y c A f A f bx f ''-= （3-15）为了计算方便，将0h x ξ=代入式(3-14)、式(3-15)，可得()[]a h A f bh f M M s s '-''+=≤0y 20c dd u 1αγγ （3-16） s y s y 0c A f A f h b f ''-=ξ （3-17） 式中 f y '——钢筋抗压强度设计值，按附录4表3取用；A's ——受压区纵向钢筋截面面积；a'——受压钢筋合力点至受压区边缘的距离。

（2）适用条件1）与单筋截面一样，为避免发生超筋情况，要求ξ≤ξb （3-18）2）保证受压钢筋应力能够达到抗压强度设计值，要求x ≥2a' （3-19）因为如果x 值太小，受压钢筋就太靠近中和轴，将得不到足够的变形，应力也就达不到抗压强度设计值，因而基本公式便不能成立。

双筋截面承受的弯矩较大，相应配置的受拉钢筋也较多，一般不必验算ρ≥ρmin 的条件。

（3）x ＜2a' 时的计算公式对于x ＜2a' 的情况，受压钢筋应力达不到f y '。

此时可近似假定受压钢筋的压力与受压混凝土的压力作用于同一直线上，且经过受压钢筋重心位置（图3-20）。

以受压钢筋合力点为力矩中心 ，可得()a h A f M M '-=≤0s y dd u 1γγ （3-20） 式(3-20)是双筋截面在x ＜2a' 时的唯一基本公式。

二、双筋矩形截面受弯构件正承载力计算（一）计算简图在进行双筋矩形截面受弯构件正截面承载力计算时，计算简图如图3-19所示。

（二）基本公式（1）设计表达式根据图3-19所示的计算简图和内力平衡条件，可列出基本设计计算公式()⎥⎦⎤⎢⎣⎡'-''+⎪⎭⎫ ⎝⎛-=≤a h A f x h bx f M M 0s y 0c d d u 21γγ （3-14） s y s y c A f A f bx f ''-= （3-15）为了计算方便，将0h x ξ=代入式(3-14)、式(3-15)，可得()[]a h A f bh f M M s s '-''+=≤0y 20c dd u 1αγγ （3-16） s y s y 0c A f A f h b f ''-=ξ （3-17） 式中 f y '——钢筋抗压强度设计值，按附录4表3取用；A's ——受压区纵向钢筋截面面积；a'——受压钢筋合力点至受压区边缘的距离。

（2）适用条件1）与单筋截面一样，为避免发生超筋情况，要求ξ≤ξb （3-18）2）保证受压钢筋应力能够达到抗压强度设计值，要求x ≥2a' （3-19）因为如果x 值太小，受压钢筋就太靠近中和轴，将得不到足够的变形，应力也就达不到抗压强度设计值，因而基本公式便不能成立。

双筋截面承受的弯矩较大，相应配置的受拉钢筋也较多，一般不必验算ρ≥ρmin 的条件。

（3）x ＜2a' 时的计算公式对于x ＜2a' 的情况，受压钢筋应力达不到f y '。

此时可近似假定受压钢筋的压力与受压混凝土的压力作用于同一直线上，且经过受压钢筋重心位置（图3-20）。

以受压钢筋合力点为力矩中心 ，可得()a h A f M M '-=≤0s y dd u 1γγ （3-20） 式(3-20)是双筋截面在x ＜2a' 时的唯一基本公式。

筋混凝土双筋矩形截面受弯构件正截面承载力
计算时
哎呀，这可是个大问题啊！我们得好好想想怎么解决这个筋混凝土双筋矩形截面受弯构件正截面承载力计算的问题。

我们得了解一下这个构件的基本情况。

它是由两个钢筋组成的矩形截面，受弯构件嘛，就是说它在受到外力作用时会发生弯曲变形。

那么，这个构件的正截面承载力到底怎么算呢？
咱们先来聊聊这个承载力的定义。

承载力就是指构件能够承受的最大压力，也就是说，如果这个构件受到了超过承载力的压力，它就会发生破坏。

那么，如何才能算出这个构件的承载力呢？这就需要用到一些数学知识了。

我们需要知道这个构件的截面尺寸。

一般来说，矩形截面的面积可以用长乘以宽来计算。

然后，我们需要考虑这个构件的材料属性。

比如说，钢筋的抗拉强度是多少？混凝土的抗压强度是多少？这些都是影响构件承载力的重要因素。

接下来，我们就要用到一些力学公式了。

比如说，钢材的屈服点和断裂点是怎么计算的？混凝土的弹性模量和抗拉强度是怎么确定的？这些问题都需要用到专业的公式和方法来进行计算。

好了，说了这么多，我们终于可以开始计算了。

我们需要根据构件的截面尺寸和材料属性来确定它的截面特性参数。

然后，我们就可以用这些参数来计算构件的正截面承载力了。

不过，这个过程还是比较复杂的，需要一定的专业知识和经验才能做好。

筋混凝土双筋矩形截面受弯构件正截面承载力的计算是一个相当专业的问题，需要我们掌握一定的数学知识和力学知识才能做好。

希望大家在学习的过程中能够保持好奇心和求知欲，不断提高自己的能力水平哦！。

筋混凝土双筋矩形截面受弯构件正截面承载力计算时嘿，伙计们！今天我们来聊聊一个很有趣的话题，那就是筋混凝土双筋矩形截面受弯构件正截面承载力计算。

别看这个话题有点专业，其实咱们老百姓也能听懂。

那就让我们一起来看看吧！我们来了解一下什么是筋混凝土双筋矩形截面受弯构件。

简单来说，就是一个用钢筋混凝土做的矩形截面，用来承受弯曲力的构件。

这个构件在咱们日常生活中可是随处可见哦，比如说楼梯、桥梁、地铁隧道等等。

这些都是靠着这种构件来抵抗弯曲力的。

那么，这个构件的正截面承载力是怎么计算的呢？咱们得先了解一下它的结构。

一般来说，这个构件有两个主要的部分：纵向筋和横向筋。

纵向筋负责抵抗垂直于截面的弯曲力，而横向筋则负责抵抗平行于截面的弯曲力。

这两个部分的受力方向是相反的，所以它们之间还有一个叫做“斜向筋”的东西，用来抵抗斜向的弯曲力。

现在，我们开始计算正截面承载力。

我们需要知道一些参数，比如纵向筋的直径、间距、箍筋的间距和尺寸等等。

然后，我们可以用一个叫做“抗弯刚度”的概念来表示这个构件的受力性能。

抗弯刚度是指单位长度的纵向筋所能抵抗的弯曲力。

有了这个概念，我们就可以用一个公式来计算正截面承载力了。

这个公式叫做“受弯承载力公式”，它的形式如下：受弯承载力 = 抗弯刚度× 截面面积其中，抗弯刚度是由纵向筋和横向筋共同决定的。

而截面面积则是由矩形截面的长和宽决定的。

有了这个公式，我们就可以根据实际情况来计算出这个构件的正截面承载力了。

不过，咱们在实际操作的时候，可不能随便瞎算哦。

因为不同的截面形状、材料强度等因素都会影响到构件的受力性能。

所以，在计算之前，咱们还需要做一些准备工作，比如查阅相关的设计规范和标准，了解不同情况下的计算方法等等。

筋混凝土双筋矩形截面受弯构件正截面承载力的计算是一个涉及到很多专业知识的问题。

但是，只要我们用心去学，就一定能够掌握这个技能。

而且，这对于我们在日常生活中使用这些构件也是非常有帮助的。

双筋矩形截面受弯构件正截面承载力计算首先，计算受力面积。

受力面积包括混凝土的受力面积和钢筋的受力
面积。

混凝土的受力面积等于矩形截面的宽度乘以混凝土的有效高度。

有
效高度通常为总高度减去两个钢筋的直径。

钢筋的受力面积等于两根钢筋
的直径乘以钢筋的长度。

其次，计算混凝土的极限应力。

混凝土的极限应力取决于混凝土的强
度等级以及截面的受拉区和受压区。

根据设计规范中给出的公式，可以计
算出混凝土的极限应力。

然后，计算钢筋的极限应力。

钢筋的极限应力取决于钢筋的强度等级
以及钢筋的屈服强度。

根据设计规范中给出的公式，可以计算出钢筋的极
限应力。

最后，根据混凝土和钢筋的极限应力以及受力面积，可以计算出正截
面的承载力。

承载力等于混凝土的受力面积乘以混凝土的极限应力加上钢
筋的受力面积乘以钢筋的极限应力。

需要注意的是，双筋矩形截面的计算还需要考虑截面的受拉区和受压
区的应力分布情况。

在截面的受拉区，混凝土和钢筋共同承担受力，应力
分布为三角形。

在截面的受压区，混凝土承担主要受力，应力分布为矩形。

总结起来，双筋矩形截面受弯构件的正截面承载力的计算方法包括确
定受力面积、计算混凝土和钢筋的极限应力，以及根据受力面积和极限应
力计算承载力。

通过这些计算，可以评估双筋矩形截面的正截面承载力，
从而进行结构设计和安全评估。

双筋矩形截面梁正截面受弯承载力计算公式的适用条件梁是建筑结构中常见的构件，承担着主要的受力任务。

在设计和施工中，对梁的承载能力进行准确的计算和评估至关重要。

而对于双筋矩形截面梁来说，其正截面受弯承载力计算公式的适用条件是关键的问题，本文将在此探讨。

一、双筋矩形截面梁简介双筋矩形截面梁是一种常见的混凝土梁截面形式，其在横截面上呈矩形状，同时设有两根钢筋以增强其受拉能力，从而使得梁的承载能力得到提高。

双筋矩形截面梁通常用于大跨度、大荷载的结构中，具有良好的承载性能和变形性能。

二、正截面受弯承载力计算公式正截面受弯承载力是指梁在受到弯矩作用时的承载能力，对于双筋矩形截面梁来说，其正截面受弯承载力计算公式通常可以用以下公式表示：1.```N_u = \phi \times \left( \alpha_1 \times A_s \times f_y +\alpha_2 \times A'_s \times f_y' \right)```其中，N_u为受弯承载力，单位为kN；\phi为折减系数，通常取为0.9；\alpha_1为混凝土应变分布影响系数，通常取为0.85；A_s为受拉钢筋面积，单位为mm^2；f_y为钢筋的屈服强度，单位为MPa；\alpha_2为受拉钢筋的应变分布影响系数，取为1.0；A'_s为受拉箍筋面积，单位为mm^2；f_y'为箍筋的屈服强度，单位为MPa。

2.```M_u = \phi \times \left( \alpha_1 \times A_s \times f_y \times d - \alpha_2 \times A'_s \times f_y' \times d' \right)```其中，M_u为弯矩抵抗矩，单位为kN·m；\phi为折减系数，取为0.9；\alpha_1为混凝土应变分布影响系数，取为0.85；A_s为受拉钢筋面积，单位为mm^2；f_y为钢筋的屈服强度，单位为MPa；d为受拉钢筋与受压区边缘的距离，单位为mm；\alpha_2为受拉钢筋的应变分布影响系数，取为1.0；A'_s为受拉箍筋面积，单位为mm^2；f_y'为箍筋的屈服强度，单位为MPa；d'为箍筋与受压区边缘的距离，单位为mm。

3双筋矩形截面受弯构件正截面承载力计算双筋矩形截面是一种常用于受弯构件的截面形式，其由钢筋和混凝土组成。

在进行正截面承载力计算时，需要考虑混凝土和钢筋的受力特性。

首先，我们需要了解混凝土和钢筋的材料特性。

混凝土的材料特性可以通过压缩强度和拉伸强度来描述。

钢筋的材料特性可以通过屈服强度和屈服点延伸度来描述。

根据受力状态的不同，正截面承载力的计算可以分为三个阶段：弯矩计算、混凝土受压区域计算和钢筋受拉区域计算。

第一阶段：弯矩计算
首先，我们需要计算受弯构件的弯矩。

弯矩可以通过外力和受力构件的几何特性来计算。

在弯矩计算中，需要考虑外部荷载和内力作用在截面上的距离。

第二阶段：混凝土受压区域计算
当受弯构件受力时，混凝土受到压力。

我们需要计算混凝土承受的压力，并通过混凝土的抗压强度来确定其是否达到承载力。

在计算混凝土受压区域的有效应力时，我们需要考虑混凝土的受拉强度和受拉区域的应力。

第三阶段：钢筋受拉区域计算
在计算钢筋的受拉区域时，我们需要考虑钢筋的悬臂长度和应力。

钢筋的受拉区域需要满足拉伸应力小于屈服应力，并考虑钢筋的强度和延伸性。

通过以上三个阶段的计算
承载力 = min(混凝土受压区域计算承载力，钢筋受拉区域计算承载力)
具体的计算公式可以根据各国规范和设计规范的要求进行调整。

需要注意的是，正截面承载力的计算仅考虑构件受弯时的承载能力，
而不考虑其他因素，如构件的轴向受力、剪切力等。

因此，在实际设计中，需要综合考虑受力构件的各种受力状态以及多种因素的影响。