双筋矩形梁正截面承载力计算

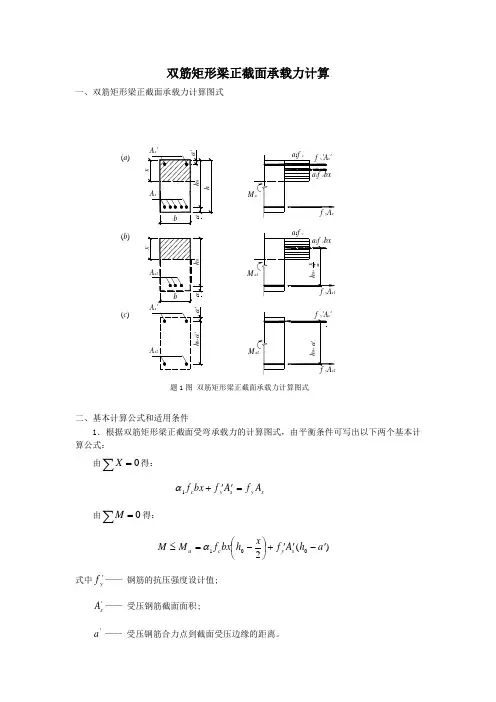
双筋矩形梁正截面承载力计算一、双筋矩形梁正截面承载力计算图式二、基本计算公式和适用条件1．根据双筋矩形梁正截面受弯承载力的计算图式，由平衡条件可写出以下两个基本计算公式：由∑=0X 得：s y sy c A f A f bx f =''+1α 由∑=0M 得：)(2001a h A f x h bx f M M sy c u '-''+⎪⎭⎫ ⎝⎛-=≤α 式中'y f —— 钢筋的抗压强度设计值; 's A —— 受压钢筋截面面积;'a —— 受压钢筋合力点到截面受压边缘的距离。

其它符号意义同前。

2．适用条件 应用式以上公式时必须满足下列适用条件：（1）0h x b ξ≤ （2）'2a x ≥如果不能满足(2)的要求，即'2a x <时，可近似取'2a x =，这时受压钢筋的合力将与受压区混凝土压应力的合力相重合，如对受压钢筋合力点取矩，即可得到正截面受弯承载力的计算公式为：)(0a h A f M M s y u '-=≤当b ξξ≤的条件未能满足时，原则上仍以增大截面尺寸或提高混凝土强度等级为好。

只有在这两种措施都受到限制时，才可考虑用增大受压钢筋用量的办法来减小ξ。

三、计算步骤（一）截面选择（设计题）设计双筋矩形梁截面时，s A 总是未知量，而's A 则可能有未知或已知这两种不同情况。

1．已知M 、b 、h 和材料强度等级，计算所需s A 和's A （1）基本数据：c f ，y f 及'y f ，1α, 1β，b ξ（2）验算是否需用双筋截面由于梁承担的弯矩相对较大，截面相对较小，估计受拉钢筋较多，需布置两排，故取mm a 60=，a h h -=0。

单筋矩形截面所能承担的最大弯矩为：M bh f M b b c u <-=)5.01(201max 1ξξα，说明需用双筋截面。

4.3.3 双筋矩形截面承载力计算如前所述，不但在截面的受拉区，而且在截面的受压区同时配有纵向受力钢筋的矩形截面，称为双筋矩形截面。

双筋矩形截面适用于下面几种情况：※结构或构件承受某种交变的作用（如地震），使截面上的弯矩改变方向；※截面承受的弯矩设计值大于单筋截面所能承受的最大弯矩，而截面尺寸和材料品种等由于某些原因又不能改变；※结构或构件的截面由于某种原因，在截面的受压区预先已经布置了一定数量的受力钢筋（如连续梁的某些支座截面）。

应该说明，双筋截面的用钢量比单筋截面的多，因此，为了节约钢材，应尽可能地不要将截面设计成双筋截面。

◆计算公式及适用条件双筋矩形截面受弯构件正截面承载力计算中，除了引入单筋矩形截面受弯构件承载力计算中的各项假定以外，还假定当x≤2a's时受压钢筋的应力等于其抗压强度设计值f'y（图4-18）。

图4-18 双筋矩形截面计算简图对于图4-18的受力情况，可以像单筋矩形截面一样列出下面两个静力平衡方程式：(4-28)(4-29)式中：A's——受压区纵向受力钢筋的截面面积；a's——从受压区边缘到受拉区纵向受力钢筋合力作用之间的距离。

对于梁，当受压钢筋按一排布置时，可取a's=35mm；当受拉钢筋按两排布置时，可取a's=60mm。

对于板，可取a's=20mm。

式(4-28)和式（4-29）是双筋矩形截面受弯构件的计算公式。

它们的适用条件是：(4-30)(4-31)满足条件式（4-30），可防止受压区混凝土在受拉区纵向受力钢筋屈服前压碎。

满足条件式（4-31），可防止受压区纵向受力钢筋在构件破坏时达不到抗压强度设计值。

因为当x<2a's时，由图4-18可知，受压钢筋的应变ε'y很小，受压钢筋不可能屈服。

当不满足条件式（4-31）时，受压钢筋的应力达不到f'y而成为未知数，这时可近似地取x=2a's，并将各力对受压钢筋的合力作用点取矩得(4-32)用式（4-32）可以直接确定纵向受拉钢筋的截面面积A s。

双筋矩形梁正截面承载力计算双筋矩形梁正截面承载力计算一、双筋矩形梁正截面承载力计算图式二、基本计算公式和适用条件1．根据双筋矩形梁正截面受弯承载力的计算图式，由平衡条件可写出以下两个基本计算公式：由∑=0X 得：s y sy c A f A f bx f =''+1α 由∑=0M 得：)(2001a h A f x h bx f M M sy c u '-''+⎪⎭⎫ ⎝⎛-=≤α 式中'y f —— 钢筋的抗压强度设计值; 's A —— 受压钢筋截面面积;'a —— 受压钢筋合力点到截面受压边缘的距离。

其它符号意义同前。

2．适用条件 应用式以上公式时必须满足下列适用条件：（1）0h x b ξ≤ （2）'2a x ≥如果不能满足(2)的要求，即'2a x <时，可近似取'2a x =，这时受压钢筋的合力将与受压区混凝土压应力的合力相重合，如对受压钢筋合力点取矩，即可得到正截面受弯承载力的计算公式为：)(0a h A f M M s y u '-=≤当b ξξ≤的条件未能满足时，原则上仍以增大截面尺寸或提高混凝土强度等级为好。

只有在这两种措施都受到限制时，才可考虑用增大受压钢筋用量的办法来减小ξ。

三、计算步骤（一）截面选择（设计题）设计双筋矩形梁截面时，s A 总是未知量，而's A 则可能有未知或已知这两种不同情况。

1．已知M 、b 、h 和材料强度等级，计算所需s A 和's A （1）基本数据：c f ，y f 及'y f ，1α, 1β，b ξ（2）验算是否需用双筋截面由于梁承担的弯矩相对较大，截面相对较小，估计受拉钢筋较多，需布置两排，故取mm a 60=，a h h -=0。

单筋矩形截面所能承担的最大弯矩为：M bh f M b b c u <-=)5.01(201max 1ξξα，说明需用双筋截面。

双筋T 形梁正截面承载力计算与设计一、双筋T 形截面设计(情况一)已知截面设计弯矩M ，T 形截面尺寸b,h,f b'h ’，材料强度c f 、y f 、y f '构件安全等级，要求计算截面所需受压钢筋s A'、受拉钢筋截面面积s A 设计步骤如下：(1)判别截面类形。

若f f c h b f ''>M 为I 类T 形截面，设计方法与单筋矩形截面类似，无需配置受压钢筋。

由平衡条件列公式(1)、(2)求出s A 。

sy ff c A f h b f ''(1))2()2('0xh A f x h x b f M s y f c u(2) (2)若f f c h b f ''<M ，该截面为Ⅱ类T 形截面，将截面受压区等效为图(b)+图(C)。

第一部分相当于受压翼缘挑出部分混凝土与其余部分受拉钢筋1s A 。

组成的受弯承载力为M 。

；第二部分相当于b*h 的双筋矩形截面部分所承担的弯矩M ：，及相对应的受拉钢筋2s A 。

由截面平衡条件可得基本公式为：1')'(s y f c A f h b b f )2)('(0xh b b f M f c u (3)若双筋矩形截面的b x x即b则截面超筋，需要在受压区设置受压钢筋s A'。

为了充分利用混凝土使截面设计更经济，令b)5.01()2(22b bc b c bh f x h bx f M ybc s f bh f A 02(4)求双筋矩形截面纯钢筋部分弯矩3M 。

213M M MM )'(''033S s y s y s y a h A f M A f A f 故双筋T 形截面受拉钢筋截面面积321s s s sA A A A 二、双筋T 形截面设计(情况二)已知截面设计弯矩M ，T 形截面尺寸b,h,f b'h ’，材料强度c f 、y f 、y f '构件安全等级，且给定了受压钢筋s A'。

双筋矩形截面梁正截面承载力计算基本公式的第二个适用条件image.png的物理意义是(1. 引言1.1 概述在土木工程领域中，结构的承载力是一个重要的设计指标。

研究和计算结构承载力的公式和条件对于确保结构的安全性至关重要。

本文将聚焦于双筋矩形截面梁正截面的承载力计算，特别关注其基本公式中第二个适用条件image.png所代表的物理意义。

1.2 文章结构为了清晰地阐述这一主题，本文将按照以下结构进行展开论述：- 第一部分将介绍双筋矩形截面梁的基本概念和特点，帮助读者理解所讨论问题的背景。

- 第二部分将详细探讨正截面承载力计算公式，并解释各参数和变量的含义与作用。

- 第三部分则专门解读第二个适用条件image.png所蕴含的物理意义，并对其合理性进行探究。

- 接下来，第四、五部分将分别阐述文章涉及到的要点一、要点二和要点三。

- 最后，通过归纳总结论、提出进一步研究方向等方式，完成全文并得出结论。

1.3 目的本文的主要目的是深入剖析双筋矩形截面梁正截面承载力计算基本公式中第二个适用条件image.png所代表的物理意义。

通过对这一条件的解读，我们可以更好地理解结构设计中的相关参数和变量，并为合理设计提供权威的指导依据。

2. 双筋矩形截面梁正截面承载力计算基本公式的第二个适用条件image.png 的物理意义：2.1 双筋矩形截面梁双筋矩形截面梁是指在混凝土梁的底部钢筋和顶部钢筋中，分别设置受拉和受压钢筋以增强梁的承载力和抗弯能力。

这种结构设计可以更有效地利用材料的性能，降低混凝土和钢材的应力，并提高整体结构的安全性。

2.2 正截面承载力计算基本公式正截面承载力计算基本公式是用于计算双筋矩形截面梁在工作状态下所能承受的最大荷载。

该公式主要包括混凝土压应力区、顶部钢筋张应力区和底部钢筋压应力区内各个区域所产生的荷载分配情况。

2.3 第二个适用条件image.png的物理意义第二个适用条件image.png描述了在正截面承载力计算时，混凝土与钢筋之间存在一定的相对滑移。