3.1.1 倾斜角与斜率
- 格式:ppt
- 大小:3.46 MB
- 文档页数:31
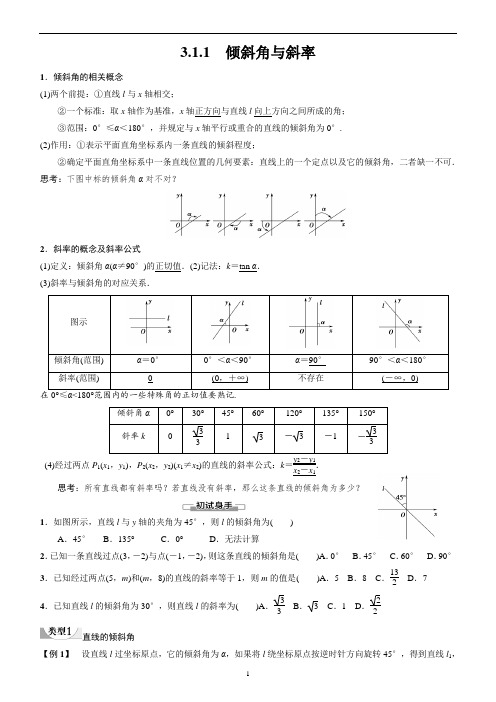
3.1.1 倾斜角与斜率1.倾斜角的相关概念(1)两个前提:①直线l 与x 轴相交;②一个标准:取x 轴作为基准,x 轴正方向与直线l 向上方向之间所成的角; ③范围:0°≤α<180°,并规定与x 轴平行或重合的直线的倾斜角为0°. (2)作用:①表示平面直角坐标系内一条直线的倾斜程度;②确定平面直角坐标系中一条直线位置的几何要素:直线上的一个定点以及它的倾斜角,二者缺一不可. 思考:下图中标的倾斜角α对不对?2.斜率的概念及斜率公式(1)定义:倾斜角α(α≠90°)的正切值.(2)记法:k =tan α. (3)斜率与倾斜角的对应关系.图示倾斜角(范围) α=0° 0°<α<90° α=90° 90°<α<180° 斜率(范围)(0,+∞)不存在(-∞,0)在0°≤α<180°范围内的一些特殊角的正切值要熟记.倾斜角α 0° 30° 45° 60° 120° 135° 150° 斜率k3313-3-1-33(4)经过两点P 1(x 1,y 1),P 2(x 2,y 2)(x 1≠x 2)的直线的斜率公式:k =y 2-y 1x 2-x 1.思考:所有直线都有斜率吗?若直线没有斜率,那么这条直线的倾斜角为多少?1.如图所示,直线l 与y 轴的夹角为45°,则l 的倾斜角为( )A .45°B .135°C .0°D .无法计算2.已知一条直线过点(3,-2)与点(-1,-2),则这条直线的倾斜角是( )A .0° B .45° C .60° D .90° 3.已知经过两点(5,m )和(m ,8)的直线的斜率等于1,则m 的值是( )A .5 B .8 C .132 D .74.已知直线l 的倾斜角为30°,则直线l 的斜率为( )A .33 B . 3 C .1 D .22直线的倾斜角【例1】 设直线l 过坐标原点,它的倾斜角为α,如果将l 绕坐标原点按逆时针方向旋转45°,得到直线l 1,那么l 1的倾斜角为( )A .α+45°B .α-135°C .135°-αD .当0°≤α<135°时,倾斜角为α+45°;当135°≤α<180°时,倾角为α-135°求直线的倾斜角的方法及两点注意(1)方法:结合图形,利用特殊三角形(如直角三角形)求角.(2)两点注意:①当直线与x 轴平行或重合时,倾斜角为0°,当直线与x 轴垂直时,倾斜角为90°. ②注意直线倾斜角的取值范围是0°≤α<180°.1.一条直线l 与x 轴相交,其向上的方向与y 轴正方向所成的角为α(0°<α<90°),则其倾斜角为( )A .αB .180°-αC .180°-α或90°-αD .90°+α或90°-α 跟踪训练2 已知直线l 向上方向与y 轴正向所成的角为30°,则直线l 的倾斜角为 .直线的斜率【例2】 (1)已知点A 的坐标为(3,4),在坐标轴上有一点B ,若k AB =4,则点B 的坐标为( )A .(2,0)或(0,-4)B .(2,0)或(0,-8)C .(2,0)D .(0,-8) (2)已知直线l 经过点A (1,2),且不经过第四象限,则直线l 的斜率k 的取值范围是( )A .(-1,0]B .[0,1]C .[1,2]D .[0,2]例3 经过下列两点的直线的斜率是否存在?如果存在,求其斜率,并确定直线的倾斜角α. (1)A (2,3),B (4,5); (2)C (-2,3),D (2,-1); (3)P (-3,1),Q (-3,10).解决斜率问题的方法(1)由倾斜角(或范围)求斜率(或范围)利用定义式k =tan α(α≠90°)解决. (2)由两点坐标求斜率运用两点斜率公式k =y 2-y 1x 2-x 1(x 1≠x 2)求解.(3)涉及直线与线段有交点问题常利用数形结合列公式求解.1.(1)已知过两点A (4,y ),B (2,-3)的直线的倾斜角为135°,则y =________.(2)过点P (-2,m ),Q (m ,4)的直线的斜率为1,则m 的值为________.跟踪训练2 如图所示,直线l 1,l 2,l 3都经过点P (3,2),又l 1,l 2,l 3分别经过点Q 1(-2,-1),Q 2(4,-2),Q 3(-3,2),计算直线l 1,l 2,l 3的斜率,并判断这些直线的倾斜角是锐角还是钝角.直线倾斜角与斜率的综合[探究问题]1.斜率公式k=y2-y1x2-x1中,分子与分母的顺序是否可以互换?y1与y2,x1与x2的顺序呢?2.斜率的正负与倾斜角范围有什么联系?命题角度1三点共线问题例3如果三点A(2,1),B(-2,m),C(6,8)在同一条直线上,求m的值.跟踪训练3已知倾斜角为90°的直线经过点A(2m,3),B(2,-1),则m的值为()A.0 B.1 C.2 D.3命题角度2数形结合法求倾斜角或斜率范围例4直线l过点P(1,0),且与以A(2,1),B(0,3)为端点的线段有公共点,求直线l的斜率和倾斜角的范围.【例3】已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点.(1)求直线l的斜率k的取值范围;(2)求直线l的倾斜角α的取值范围.将本例变为:已知A(3,3),B(-4,2),C(0,-2).若点D在线段BC上(包括端点)移动,求直线AD的斜率的变化范围.1.求直线斜率的取值范围时,通常先结合图形找出倾斜角的范围,再得到斜率的范围.2.利用斜率可解决点共线问题,点A,B,C共线⇔k AB=k AC或k AB与k AC都不存在.3.y2-y1x2-x1的几何意义是直线的斜率,用之可通过几何方法解决函数的值域问题.一、选择题1.下列说法中正确的是( )A .一条直线和x 轴的正方向所成的正角,叫做这条直线的倾斜角B .直线的倾斜角α的取值范围是[0°,180°]C .和x 轴平行的直线的倾斜角为180°D .每一条直线都存在倾斜角,但并非每一条直线都存在斜率 2.已知l 1⊥l 2,直线l 1的倾斜角为60°,则直线l 2的倾斜角为( ) A .60° B .120° C .30° D .150°3.若直线过坐标平面内两点(1,2),(4,2+3),则此直线的倾斜角是( ) A .30° B .45° C .60° D .90°4.已知直线l 的斜率的绝对值等于3,则直线l 的倾斜角为( ) A .60° B .30° C .60°或120° D .30°或150° 5.下列各组中,三点能构成三角形的三个顶点的为( )A .(1,3)、(5,7)、(10,12)B .(-1,4)、(2,1)、(-2,5)C .(0,2)、(2,5)、(3,7)D .(1,-1)、(3,3)、(5,7) 6.若图中直线l 1、l 2、l 3的斜率分别为k 1、k 2、k 3,则( ) A .k 1<k 2<k 3 B .k 3<k 1<k 2 C .k 3<k 2<k 1 D .k 1<k 3<k 27.一条直线l 与x 轴相交,其向上的方向与y 轴正方向所成的角为α(0°<α<90°),则其倾斜角为( ) A .α B .180°-α C .180°-α或90°-α D .90°+α或90°-α 8.已知直线l 过点A (1,2),且不过第四象限,则直线l 的斜率k 的最大值是( ) A .2 B .1 C.12 D .0二、填空题9.若三点A (2,2),B (a,0),C (0,b )(ab ≠0)共线,则1a +1b的值等于 .10.已知点A (1,2),若在坐标轴上有一点P ,使直线P A 的倾斜角为135°,则点P 的坐标为 . 11.若经过点A (1-t,1+t )和点B (3,2t )的直线的倾斜角为钝角,则实数t 的取值范围是 . 12.若直线l 经过A (2,1),B (1,m 2)(m ∈R )两点,则直线l 的倾斜角的取值范围为 . 三、解答题13.已知坐标平面内两点M (m +3,2m +5),N (m -2,1).(1)当m 为何值时,直线MN 的倾斜角为锐角?(2)当m 为何值时,直线MN 的倾斜角为钝角? (3)直线MN 的倾斜角可能为直角吗?四、探究与拓展14.已知坐标平面内三点A(-1,1),B(1,1),C(2,3+1).若D为△ABC的边AB上一动点,则直线CD的斜率k的取值范围为()A.[33,3] B.[0,33]∪[3,+∞) C.[33,+∞) D.[3,+∞)15.已知坐标平面内三点P(3,-1),M(6,2),N(-3,3),直线l过点P.若直线l与线段MN相交,求直线l的倾斜角的取值范围.3.1.2两条直线平行与垂直的判定1.两条直线平行与斜率之间的关系类型斜率存在斜率不存在条件α1=α2≠90°α1=α2=90°对应关系l1∥l2⇔k1=k2l1∥l2⇔两直线斜率都不存在图示思考1如图,设对于两条不重合的直线l1与l2,其倾斜角分别为α1与α2,斜率分别为k1与k2,若l1∥l2,α1与α2之间有什么关系?k1与k2之间有什么关系?思考2对于两条不重合的直线l1与l2,若k1=k2,是否一定有l1∥l2?为什么?2.两条直线垂直与斜率之间的关系图示对应关系l1⊥l2(两条直线的斜率都存在,且都不为零)⇔k1k2=-1l1的斜率不存在,l2的斜率为0⇒l1⊥l2思考1如图,设直线l1与l2的倾斜角分别为α1与α2,斜率分别为k1与k2,且α1<α2,若l1⊥l2,α1与α2之间有什么关系?为什么?思考2 已知tan(90°+α)=-1tan α,据此,如何推出思考1中两直线的斜率k 1、k 2之间的关系?思考3 如果两直线的斜率存在且满足k 1·k 2=-1,是否一定有l 1⊥l 2?如果l 1⊥l 2,一定有k 1·k 2=-1吗?为什么?1.已知A (2,0),B (3,3),直线l ∥AB ,则直线l 的斜率k 等于( )A .-3 B .3 C .-13 D .132.已知直线l 1的斜率k 1=2,直线l 2的斜率k 2=-12,则l 1与l 2( )A .平行B .垂直C .重合D .非以上情况3.l 1过点A (m ,1),B (-3,4),l 2过点C (0,2),D (1,1),且l 1∥l 2,则m =________.两直线平行的判定及应用【例1】 根据下列给定的条件,判断直线l 1与直线l 2是否平行.(1)l 1经过点A (2,1),B (-3,5),l 2经过点C (3,-3),D (8,-7); (2)l 1经过点E (0,1),F (-2,-1),l 2经过点G (3,4),H (2,3); (3)l 1的倾斜角为60°,l 2经过点M (1,3),N (-2,-23); (4)l 1平行于y 轴,l 2经过点P (0,-2),Q (0,5).1.已知l 1经过点A (-3,3),B (-8,6),l 2经过点M ⎝⎛⎭⎫-212,6,N ⎝⎛⎭⎫92,-3,求证:l 1∥l 2.跟踪训练2 已知A (1,-a +13),B (0,-13),C (2-2a,1),D (-a,0)四点,当a 为何值时,直线AB 和直线CD平行.两条直线垂直关系的判定【例2】 判断下列各题中l 1与l 2是否垂直.(1)l 1经过点A (-1,-2),B (1,2);l 2经过点M (-2,-1),N (2,1); (2)l 1的斜率为-10;l 2经过点A (10,2),B (20,3);(3)l 1经过点A (3,4),B (3,10);l 2经过点M (-10,40),N (10,40).例3已知三点A(5,-1),B(1,1),C(2,3).求证:△ABC是直角三角形.使用斜率公式判定两直线垂直的步骤(1)一看:就是看所给两点的横坐标是否相等.若相等,则直线的斜率不存在;若不相等,则进行第二步.(2)二代:就是将点的坐标代入斜率公式.(3)求值:计算斜率的值,进行判断,尤其是点的坐标中含有参数时,应用斜率公式对参数进行讨论.1.已知直线l1经过点A(3,a),B(a-1,2),直线l2经过点C(1,2),D(-2,a+2).若l1⊥l2,求a的值.跟踪训练2已知定点A(-1,3),B(4,2),以A,B为直径作圆,与x轴有交点C,求交点C的坐标.两直线平行与垂直的综合应用[探究问题]1.已知△ABC的三个顶点坐标A(5,-1),B(1,1),C(2,3),你能判断△ABC的形状吗?2.已知定点A(-1,3),B(4,2),以AB为直径作圆,若圆与x轴有交点C.如何确定点C的坐标?【例3】△ABC的顶点A(5,-1),B(1,1),C(2,m),若△ABC是以点A为直角顶点的直角三角形,求m 的值.1.本例中若改为∠A为锐角,其他条件不变,如何求解m的值?2.若将本例中的条件“点A为直角顶点”去掉,改为若△ABC为直角三角形,如何求解m的值?例4已知四边形ABCD的顶点B(6,-1),C(5,2),D(1,2).若四边形ABCD为直角梯形,求A点坐标.引申探究本例中若将条件“四边形ABCD 为直角梯形”改为AC ∥BD ,AB ∥CD ,求A 点坐标.反思与感悟 有关两条直线垂直与平行的综合问题,一般是根据已知条件列方程(组)求解.如果涉及到有关四边形已知三个顶点求另外一个顶点,注意判断图形是否唯一,以防漏解.跟踪训练3 已知矩形ABCD 的三个顶点的坐标分别为A (0,1),B (1,0),C (3,2),求第四个顶点D 的坐标.一、选择题1.设点P (-4,2),Q (6,-4),R (12,6),S (2,12),下面四个结论:①PQ ∥SR ;②PQ ⊥PS ;③PS ∥QS ;④PR ⊥QS . 其中正确的个数是( ) A .1 B .2 C .3D .42.如果直线l 1的斜率为a ,l 1⊥l 2,那么直线l 2的斜率为( ) A.1a B .a C .-1aD .-1a或不存在3.若直线l 1的倾斜角为135°,直线l 2经过点P (-2,-1),Q (3,-6),则直线l 1与l 2的位置关系是( ) A .垂直 B .平行 C .重合 D .平行或重合4.已知点A (m,3),B (2m ,m +4),C (m +1,2),D (1,0),且直线AB 与直线CD 平行,则m 的值为( ) A .1 B .0 C .0或1D .0或25.已知直线l 的倾斜角为20°,直线l 1∥l ,直线l 2⊥l ,则直线l 1与l 2的倾斜角分别是( ) A .20°,110° B .70°,70° C .20°,20°D .110°,20°6.顺次连接A (-4,3),B (2,5),C (6,3),D (-3,0)所构成的图形是( ) A .平行四边形 B .直角梯形 C .等腰梯形 D .以上都不对 二、填空题7.已知直线l 1经过点A (0,-1)和点B (4a ,1),直线l 2经过点M (1,1)和点N (0,-2),若l 1与l 2没有公共点,则实数a 的值为________.8.已知A (2,0),B (3,3),直线l ∥AB ,则直线l 的倾斜角为________.9.若点P (a ,b )与点Q (b -1,a +1)关于直线l 对称,则直线l 的倾斜角α为________.10.直线l 1,l 2的斜率k 1,k 2是关于k 的方程2k 2-3k -b =0的两根,若l 1⊥l 2,则b =____________;若l 1∥l 2,则b =____________.11.已知点A (-3,-2),B (6,1),点P 在y 轴上,且∠BAP =90°,则点P 的坐标是______.三、解答题12.当m为何值时,过两点A(1,1),B(2m2+1,m-2)的直线:(1)倾斜角为135°;(2)与过两点(3,2),(0,-7)的直线垂直;(3)与过两点(2,-3),(-4,9)的直线平行.四、探究与拓展13.已知P(-2,m),Q(m,4),M(m+2,3),N(1,1),若直线PQ∥直线MN,则m的值为______.14.已知△ABC的顶点A(1,3),B(-1,-1),C(2,1),求△ABC的边BC上的高AD的斜率和垂足D的坐标.。

3.1.1倾斜角与斜率【教学目标】:1. 理解直线的倾斜角的定义,掌握直线倾斜角的范围。
2. 理解直线的斜率,掌握过两点的直线的斜率公式。
3. 掌握直线斜率和倾斜角之间的关系。
教学重点:斜率的概念,用代数方法刻画直线的斜率,过两点的直线斜率的计算公式。
教学难点:直线的斜率和倾斜角的关系,【复习回顾】:问题1.在平面直角坐标系中, 一次函数y=kx+b 的图象是什么?其中 k , 如何? 问题2.我们知道,经过两点有且只有(确定)一条直线,那么,经过一点 的位置是否能够确定?这些直线有什么联系?【数学建构】1. 直线的倾斜角:当直线 I 与X 轴相交时,取X 轴作为基准,X 轴正向与直线 间所成的角a 叫做直线I 的倾斜角.问题3.下列各图中标出的角 a 是直线的倾斜角吗?特别:当直线I 与x 轴平行或重合时,规定 a =0. 问题4.直线倾斜角a 的取值范围是什么? 问题5.在日常生活中,我们常说这个山坡很陡峭,有时也说坡度,这里的陡峭和坡度 说的是山坡与水平面之间的一个什么关系呢? 问题6.如何度量直线的倾斜程度?2. 直线的斜率:倾斜角不是 90。
的直线,它的倾斜角的正切叫做这条直线的斜率,常用表示,即 k=tan a.问题7.我们知道两点确定一条直线,那么已知直线上两点坐标,如何才能求出它的倾 斜角和斜率呢?如:已知A(2 , 3)、B( — 1 , 4),则直线AB 的斜率是多少? 说明:(1)当X 1 = x 2时,公式右边无意义,直线的斜率不存在,倾斜角a = 90°,直线与x 轴垂直;(2) k 与P 1、P 2的顺序无关,即y 1、y 2和X 1、X 2在公式中的前后次序可以同时交换, 但分子与分母不能交换;(3) 斜率k 可以不通过倾斜角而直接由直线上两点的坐标求得;(4) 当y 1 = y 2时,斜率k = 0,直线的倾斜角 a = 0 °,直线与x 轴平行或重合.(5)求直线的倾斜角可以由直线上两点的坐标先求斜率而得到 .电 / / f "y f b 的几何意义 P 的直线I I 向上方向之【数学应用】例1、已知 A (3, 2), B (-4, 1), C (0, -1),求直线线AB,BC,CA的斜率,并判断这些直的倾斜角是锐角还是钝角。

数学必修二 第三章 直线与方程 青岛天龙中学高二数学备课组 数学必修二 第三章 直线与方程 青岛天龙中学高二数学备课组第 1 页 共 2 页第 2 页 共 2 页§3.1.1倾斜角与斜率一、学习目标:1.正确理解直线的倾斜角和斜率的概念.2.理解直线的倾斜角的唯一性.掌握直线的倾斜角与斜率的关系.二、学习重、难点重点: 直线的倾斜角、斜率的概念和斜率公式的应用.难点: 直线的倾斜角、斜率的对应关系,求直线的倾斜角和斜率的范围.三、课前预习:1、阅读教材P82-86,注意逐字逐句仔细审题,认真思考、不会的先绕过,做好记号。
2、把学案中自己易忘、易出错的知识点和疑难问题以及解题方法规律,及时整理在解题本,多复习记忆.(尤其是正切的三角函数值,斜率的计算公式必须牢记),四、知识衔接:1:一次函数的图象的形状是2:确定一次函数的图象的条件是3:锐角正切函数的定义五、新课学习;1. 直线的倾斜角:①定义:当直线l 与x 轴相交时,我们取x 轴作为基准, 叫做直线l 的倾斜角....特别地,当直线l 与x 轴平行或重合时, 规定α= 0°. ②范围:倾斜角α的取值范围是 特别:当 时,称直线l 与x 轴垂直2.直线的斜率:一条直线的倾斜角α(α≠90°)的 叫做这条直线的斜率,斜率常用小写字母k 表示,即k = .①当直线l 与x 轴平行或重合时, α= , k = ;②当直线l 与x 轴垂直时,α= , k .试画出y=tan α α∈(0,π)的函数图像注:(1)时,斜率不存在。
当时,当的增大而减小;随的增大而增大,但随时,,当的增大而增大;也随的增大而增大,随时,当2;0 0,0)2(,0 )2 ,0 (πααααππαααπα===<∈>∈k k k k k k k (2)平面内任何一条直线都有唯一的倾斜角,但不是每一条直线都有,倾斜角为90°的直线没有斜率,在使用斜率来研究直线时,经常要对直线是否有斜率分情形讨论. 3. 直线的斜率公式:①已知直线的倾斜角α,则k=②经过两个定点 P 1(x 1,y 1) , P 2(x 2,y 2) 的直线:若x 1≠x 2,则直线P 1P 2 的斜率存在,k= 若x 1=x 2,则直线P 1P 2的斜率 例1:已知A(3, 2), B(-4, 1), C(0, -1), 求直线AB 、BC 、CA 的斜率, 并判断它们的倾斜角是钝角还是锐角. 例2:在平面直角坐标系中, 画出经过原点且斜率分别为1、 -1、2及-3的直线L 1、L 2、L 3、L 4【当堂检测】1. 在下列叙述中:所有正确命题的序号是①一条直线的倾斜角为θ,则它的斜率k= tan θ; ②若直线的斜率k=-1,则它倾斜角为135°;③经过A (-1,0),B (-1,3)两点的直线的倾斜角为90°; ④直线y=1的倾斜角为45°。



3.1直线的倾斜角与斜率3.1.1倾斜角与斜率学习目标核心素养1.理解直线的斜率和倾斜角的概念.2.理解直线倾斜角的唯一性及直线斜率的存在性.3.了解斜率公式的推导过程,会应用斜率公式求直线的斜率.1. 通过倾斜角概念的学习,提升直观想象的数学素养.2. 通过斜率的学习,培养逻辑推理和数学运算的数学素养.1.倾斜角的相关概念(1)两个前提:①直线l与x轴相交;②一个标准:取x轴作为基准,x轴正方向与直线l向上方向之间所成的角;③范围:0°≤α<180°,并规定与x轴平行或重合的直线的倾斜角为0°.(2)作用:①表示平面直角坐标系内一条直线的倾斜程度;②确定平面直角坐标系中一条直线位置的几何要素:直线上的一个定点以及它的倾斜角,二者缺一不可.思考:下图中标的倾斜角α对不对?[提示]都不对.2.斜率的概念及斜率公式(1)定义:倾斜角α(α≠90°)的正切值.(2)记法:k=tan α.(3)斜率与倾斜角的对应关系.图示倾斜角(范围) α=0°0°<α<90°α=90°90°<α<180°斜率(范围)0 (0,+∞) 不存在(-∞,0)(4)经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线的斜率公式:k=y2-y1 x2-x1.思考:所有直线都有斜率吗?若直线没有斜率,那么这条直线的倾斜角为多少?[提示]不是.若直线没斜率,则其倾斜角为90°.1.如图所示,直线l与y轴的夹角为45°,则l的倾斜角为()A.45°B.135°C.0°D.无法计算B[根据倾斜角的定义知,l的倾斜角为135°.]2.已知一条直线过点(3,-2)与点(-1,-2),则这条直线的倾斜角是() A.0°B.45°C.60°D.90°A[∵k=04=0,∴θ=0°.]3.已知经过两点(5,m)和(m,8)的直线的斜率等于1,则m的值是()A.5 B.8C.132D.7C[由斜率公式可得8-mm-5=1,解之得m=132.]4.已知直线l的倾斜角为30°,则直线l的斜率为()A.33B. 3 C.1 D.22A[由题意可知,k=tan 30°=3 3.]直线的倾斜角时针方向旋转45°,得到直线l1,那么l1的倾斜角为()A.α+45°B.α-135°C.135°-αD.当0°≤α<135°时,倾斜角为α+45°;当135°≤α<180°时,倾角为α-135°D[根据题意,画出图形,如图所示:因为0°≤α<180°,显然A,B,C未分类讨论,均不全面,不合题意.通过画图(如图所示)可知:当0°≤α<135°,l1的倾斜角为α+45°;当135°≤α<180°时,l1的倾斜角为45°+α-180°=α-135°.故选D.]求直线的倾斜角的方法及两点注意(1)方法:结合图形,利用特殊三角形(如直角三角形)求角.(2)两点注意:①当直线与x 轴平行或重合时,倾斜角为0°,当直线与x 轴垂直时,倾斜角为90°.②注意直线倾斜角的取值范围是0°≤α<180°.1.一条直线l 与x 轴相交,其向上的方向与y 轴正方向所成的角为α(0°<α<90°),则其倾斜角为( )A .αB .180°-αC .180°-α或90°-αD .90°+α或90°-αD [如图,当l 向上方向的部分在y 轴左侧时,倾斜角为90°+α;当l 向上方向的部分在y 轴右侧时,倾斜角为90°-α.故选D.]直线的斜率AB 则点B 的坐标为( )A .(2,0)或(0,-4)B .(2,0)或(0,-8)C .(2,0)D .(0,-8)(2)已知直线l 经过点A (1,2),且不经过第四象限,则直线l 的斜率k 的取值范围是( )A .(-1,0]B .[0,1]C .[1,2]D .[0,2](1)B (2)D [(1)设B (x ,0)或(0,y ),∵k AB =43-x 或k AB =4-y 3,∴43-x =4或4-y3=4,∴x =2,y =-8,∴点B 的坐标为(2,0)或(0,-8).(2)由图可知当直线位于如图阴影部分所示的区域内时,满足题意,所以直线l 的斜率满足0≤k ≤2.故选D.]解决斜率问题的方法(1)由倾斜角(或范围)求斜率(或范围)利用定义式k=tan α(α≠90°)解决.(2)由两点坐标求斜率运用两点斜率公式k=y2-y1x2-x1(x1≠x2)求解.(3)涉及直线与线段有交点问题常利用数形结合列公式求解.2.(1)已知过两点A(4,y),B(2,-3)的直线的倾斜角为135°,则y=________.(2)过点P(-2,m),Q(m,4)的直线的斜率为1,则m的值为________.(1)-5(2)1[(1)直线AB的斜率k=tan 135°=-1,又k=-3-y2-4,由-3-y2-4=-1,得y=-5.(2)由题意得4-mm+2=1,∴m=1.]直线倾斜角与斜率的综合1.斜率公式k=y2-y1x2-x1中,分子与分母的顺序是否可以互换?y1与y2,x1与x2的顺序呢?[提示]斜率公式中分子与分母的顺序不可以互换,但y1与y2和x1与x2可以同时互换顺序,即斜率公式也可写为k=y1-y2x1-x2. 2.斜率的正负与倾斜角范围有什么联系?[提示]当k=tan α<0时,倾斜角α是钝角;当k=tan α>0时,倾斜角α是锐角;当k =tan α=0时, 倾斜角α是0°.【例3】 已知两点A (-3,4),B (3,2),过点P (1,0)的直线l 与线段AB 有公共点.(1)求直线l 的斜率k 的取值范围; (2)求直线l 的倾斜角α的取值范围.思路探究:作图――――――――――→直线与线段有公共点倾斜角介于直线PB 与P A 的倾斜角之间―――→求斜率求斜率范围及倾斜角范围 [解] 如图所示,由题意可知k P A =4-0-3-1=-1,k PB =2-03-1=1.(1)要使直线l 与线段AB 有公共点,则直线l 的斜率k 的取值范围是k ≤-1或k ≥1.(2)由题意可知,直线l 的倾斜角介于直线PB 与P A 的倾斜角之间,又PB 的倾斜角是45°,P A 的倾斜角是135°,所以α的取值范围是45°≤α≤135°.将本例变为: 已知A (3,3),B (-4,2),C (0,-2).若点D 在线段BC 上(包括端点)移动,求直线AD 的斜率的变化范围.[解] 如图所示.当点D 由B 运动到C 时,直线AD 的斜率由k AB 增大到k AC ,又k AB =3-23-(-4)=17,k AC =3-(-2)3-0=53,所以直线AD 的斜率的变化范围是⎣⎢⎡⎦⎥⎤17,53.1.求直线斜率的取值范围时,通常先结合图形找出倾斜角的范围,再得到斜率的范围.2.利用斜率可解决点共线问题,点A,B,C共线⇔k AB=k AC或k AB与k AC 都不存在.3.y2-y1x2-x1的几何意义是直线的斜率,用之可通过几何方法解决函数的值域问题.直线的斜率和倾斜角反映了直线的倾斜程度,二者紧密相连,如下表:直线情况平行于x轴垂直于x轴α的大小0°0°<α<90°90°90°<α<180°k的范围0 k>0 不存在k<0k的增减情况k随α的增大而增大k随α的增大而增大1.对于下列命题:①若α是直线l的倾斜角,则0°≤α<180°;②若k是直线的斜率,则k∈R;③任一条直线都有倾斜角,但不一定有斜率;④任一条直线都有斜率,但不一定有倾斜角.其中正确命题的个数是()A.1 B.2C.3D.4C[由倾斜角和斜率概念可知①②③正确.]2.已知直线AB与直线AC有相同的斜率,且A(1,0),B(2,a),C(a,1),则实数a的值是________.1±52 [依题意:k AB =k AC ,即a -02-1=1-0a -1, 解得a =1±52.]3.经过A (m ,3),B (1,2)两点的直线的倾斜角α的取值范围是________.(其中m ≥1)(0°,90°] [当m =1时,倾斜角α=90°,当m >1时,tan α=3-2m -1>0,∴0°<α<90°,故0°<α≤90°.]4.已知交于M (8,6)点的四条直线l 1,l 2,l 3,l 4的倾斜角之比为1∶2∶3∶4,又知l 2过点N (5,3),求这四条直线的倾斜角.[解] l 2的斜率为6-38-5=1,∴l 2的倾斜角为45°,由题意可得:l 1的倾斜角为22.5°,l 3的倾斜角为67.5°,l 4的倾斜角为90°.。