当前位置：文档之家 › 第三章 非正弦周期电路分析

第三章 非正弦周期电路分析

  • 格式：ppt
  • 大小：1.72 MB
  • 文档页数：86

下载文档原格式

  / 86

合集下载

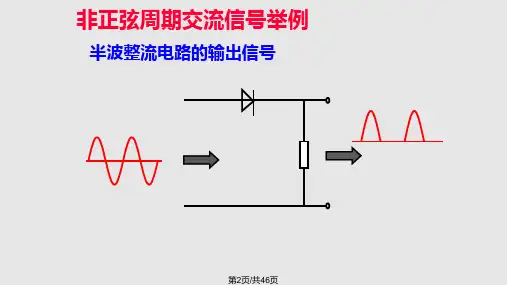
非正弦周期电流的电路.pptx

非正弦周期电流的电路.pptx
k p
第39页/共46页
一、非正弦周期函数的平均值
若 u(wt) = U0 + U km sin(kwt + k ) k =1
正弦量的平均值为0
则其平均值为： (直流分量)
U AV
=
1
2
2
0 u(wt)dwt = U0
第40页/共46页
二、非正弦周期函数的有效值
若 u(wt) = U0 + U km sin(kwt + k ) k =1
is3
=
100 sin 3
3106 t
μA
Z (3w1) = 374 .5 89.19
U 3 = IS 3 Z (3w1)
= 33.3 10 6 374 .5 89.19 2
= 12.47 89.2 mV 2
第25页/共46页
4. 五次谐波 作用
20Ω
R
is3
C L u3
is5
直流分量+基波+三次谐波
第10页/共46页
三次谐波
频谱图
时域
U
Um
T
t
4U m
=U0
U0
3
w 3w
频域
U0
5w
5w
U = 4Um (sinwt + 1 sin 3wt + 1 sin 5wt +)
3
5
时域 周期性函数
第11页/共46页
频域 离散谱线
§5.3 非正弦周期交流电路的分析 和计算 要点
f (wt) = A0 + Bkm sin kwt + Ckm cos kwt
k =1
k =1

非正弦周期电路分析

非正弦周期电路分析

f(=w/2p)=1/T
u i
☣除了主要的基频成分外， 0
wt
波形还含有大量谐波成分。
2p
非正弦周期电路的基本概念
1.3 傅立叶级数的三角形式
设 f(t)为电压或电流的非正弦周期函数，其角频率为
w ，即 :
式中， T为周期函数f(t) ，k =0, 1, 2,
如果给定的周期函数满足狄里赫利条件，可展开为傅 立叶级数，即:
从
中看到，如果电流波形有较大畸变，将导
致is1 / is较小 ，因此功率因数也会很小。
根据
可得:
电力电子技术的基本概况
T=1/f
非正弦周期电路的基本概念
利用波形对称性，可简化下式中系数ah和bh的计算:
表3.1是根据函数的对称性及所需要的条件，分别 给出了ah和bh的表达式。
对称性函数的傅立叶系数
对称性 条件 偶函数 奇函数
半波
电路和磁路的基本概念 ah 和 bh
h为偶数 h为奇数 h为奇数
对称性 条件
偶拓扑
偶函数 及半波
奇拓扑
奇函数 及半波
电路和磁路的基本概念
ah 和 bh
h为奇数或偶数
h为奇数
h为偶数
h为奇数或偶数 h为奇数 h为偶数
非正弦周期电路的基本概念
例 求图中所示非正弦周期信号f(t)
f(t) A
的傅里叶级数展开式。
-T-T/2 0 T/2 T t
解 由图可知f(t)在一个周期内的表达式为:
is us is1
生了严重畸变的波形。 0
wt
✼假设输入的电压为标准
j1
idis
的正弦电压:
w = w1，f = f1

电路分析_非正弦周期电流电路

电路分析_非正弦周期电流电路
其中
u U 0 U km sin(k t uk )
k 1

i I 0 I km sin(k t ik )
k 1
1 T P [U 0 U km sin(kt uk )][I 0 I km sin(kt ik )]dt T 0 k 1 k 1
图6.7正弦波u1 u3 u5 合成非正弦波u
• 6.2.2 非正弦波的分解
任何一 个周期性非正弦量 可以分解为一系列不 同频率的正弦量。 由高等数学知识可知，凡满足狄利赫里条件的周 期函数都可以分解为傅里叶级数。在电工技术中所遇 到的周期性非正弦量，一般情况下都能满足狄利赫里 条件，因此都可以分解为傅里叶级数。
电路分析_非正弦周期电流电路
6.1 非正弦周期量
• 常见非正弦周期量
图6.1 全波整流电压波形
图6.2 半波整流电压波形
图6.3 尖脉冲波形
图6.4 矩形脉冲波形
图6.5 锯齿波形
6.2 非正弦周期信号的谐波分析
• 6.2.1 非正弦波的合成
、
图6.6 正弦波
图6.6 正弦波u1 u3 合成非正弦波u
使某一频率范围内的谐波分量顺利通过，而其它频率的谐波 分量受到抑制的滤波电路称为带通滤波器

型

型
图6.15 带通滤波器
6.4.4带阻滤波器
• 使某一频率范围内的谐波分量受到抑制，而其它频率的谐
波分量顺利通过的滤波电路称为带阻滤波器

型

图6.16 带阻滤波器
型
非正弦周期电流平均值为
I av 1 T

T
T
0
| i |d t
非正弦周期电压平均值为

电路原理课件-非正弦周期电流电路分析

电路原理课件-非正弦周期电流电路分析

Z ( j3 ) I 0.125e j179.95 V U 3m 1 3m Z ( j5 ) I 0.0416e j0.01 V U 5m 1 5m
U 7 m Z ( j71 ) I 7 m 0.0208 V
(4) 将响应的直流分量及各谐波分量的时间函数式相 叠加，求出电压响应。
基波电流单独作用时：
i1 cos 1t mA
1e j90 mA I1 m
Z (j ) I 50e j90 V U1 m 1 1m
当3次、5次、7次谐波单独作用时：
1 e j90 mA I 3m 3 1 e j90 mA I 5m 5 1 e j90 mA I7m 7
n 1
值得指出：一个周期函数是否具有半波对称性，仅决 定于该函数的波形，但是，一个周期函数是否为奇函 数或偶函数则不仅与该函数的波形有关，而且和时间 起点的选择有关。
§82 线性电路对周期性激励的稳态响应
步骤：
1、将周期性激励分解为傅里叶级数； 2、根据叠加定理，分别计算激励的直流分量和各 次谐波分量单独作用时在电路中产生的稳态响应； 3、将直流分量和各谐波激励所产生的时域响应叠 加，即得线性电路对非正弦周期性激励的稳态响应。
An a b
2 n 2 n
an θn arctan bn
A0 f (t ) An sin( nω1t θn ) 2 n 1
其中， A0 a0
A0 f (t ) An sin( nω1t θn ) 2 n 1
A0 常数项（直流分量） 2 A1 sin(ω1t θ1 ) 基波(fundamental wave)
a0 1 2 T

非正弦周期电流电路分析

非正弦周期电流电路分析

非正弦周期电流电路分析简介非正弦周期电流电路是一种电路，其中电流的波形不是正弦曲线。

这种电路通常由非线性元件或者非理想元件构成，导致电流波形发生变化。

本文将对非正弦周期电流电路进行分析，探讨其中的特点和应用。

非正弦周期电流的产生非正弦周期电流可以由多种方式产生，包括以下几种常见情况：1.非线性元件的非线性特性导致电流波形变化。

例如，二极管在反向偏置时会产生非线性特性，导致电流波形不是正弦曲线。

2.非理想元件的特性导致电流波形变化。

例如，电感元件的饱和和饱和恢复会导致电流波形非正弦。

3.控制信号或输入信号的特性导致电流波形变化。

例如，方波、脉冲或其他非正弦的控制信号输入到电路中时，会引起电流波形的变化。

非正弦周期电流的特点非正弦周期电流具有以下几个特点：1.波形失真：由于非线性元件或非理想元件的特性，非正弦周期电流的波形会失真。

这种失真包括高次谐波的增加或者波形畸变。

2.频谱分布：非正弦周期电流的频谱分布比正弦电流更加复杂。

由于波形的非线性和不规则，频谱中会包含多个谐波成分。

3.能量损耗：非正弦周期电流的能量损耗比正弦电流更大。

由于电流波形的非正弦特性，导致电路中存在额外的损耗。

4.信号干扰：非正弦周期电流会产生更多的信号干扰。

由于频谱中存在多个谐波成分，这些谐波会干扰其他电路或设备的正常运行。

非正弦周期电流电路分析方法对于非正弦周期电流电路的分析，可以采用以下方法：1.线性电路分析：首先将非正弦周期电流分解为多个谐波成分，然后对每个谐波成分进行线性电路分析。

通过将各个谐波成分的响应叠加，可以得到整个非正弦周期电流电路的响应。

2.时域分析：使用时域分析方法，通过观察电流波形的变化来理解非正弦周期电流电路的工作情况。

这种方法适用于简单的电路，可以直接观察电流波形的特点。

3.频域分析：使用频域分析方法，对非正弦周期电流的频谱进行分析。

通过观察频谱中的谐波成分，可以了解电流波形的非正弦特性。

4.仿真分析：使用电路仿真软件，对非正弦周期电流电路进行仿真分析。

非正弦电流周期电路分析

非正弦电流周期电路分析

例题
8.1
求图所示周期性方波的傅里叶展开式，并画其频谱。 求图所示周期性方波的傅里叶展开式，并画其频谱。
A t
O
T/2
T
2 T 1 2π ak = ∫ f (t)cos(kωt)dt = ∫ f (t)cos(kωt)d(ω t) T 0 π 0 2 T 1 2π bk = ∫ f (t)sin(kωt)dt = ∫ f (t)sin(kωt)d(ωt) T 0 π 0
f (t) = A + ∑[ Amk cosψk cos(kωt) Amk sinψk sin(kωt)] 0
∞
= A + ∑Amk cos(kωt +ψk ) 0
k =1
∞
k =1
(8.6)
2 2 A = ak + bk mk
(8.1)、(8.6)式比较，得 、 式比较， 式比较
ak = Amk cosψk
5ω 7ω
kω 9ω
三角波的频谱图
其谐波振幅与k 其谐波振幅与 2成反比
下面是几种常见周期函数的傅里叶级数 f ( t )的波形图 的波形图 f ( t )的傅里叶级数 的傅里叶级数
f (ωt) = 1 4A 1 (sin ωt + sin 3ωt + sin 5ωt π 3 5
1 T /2 A A = ∫ Ad t = 0 T 0 2 2 T /2 2A T /2 ak = ∫ Acos(kωt)dt = cos(kωt)d(kωt) T 0 kωT ∫0 2A 2A 2π ω = sin(kωt) T /2 = sin(kω ) =0 0 kωT kωT 2
图8.4 周期性方波
2．谐波分析— 将周期函数分解为恒定分量、基波分量和各次谐 谐波分析— 将周期函数分解为恒定分量、 波的方法。 波的方法。 谐波振幅A 变动的情形如图8.3所示 谐波振幅 mk随角频率 kω变动的情形如图 所示 变动的情形如图 A1 m 图中竖线称为谱线，长度表示A 的量值； 图中竖线称为谱线，长度表示 mk的量值； 相邻两谱线的间隔等于基波角频率ω。 相邻两谱线的间隔等于基波角频率 。这 A2 m 种谱线间具有一定间隔的频谱称为离散 A3 m A4 m A 5 m A6 m 频谱。同样可以画出相位频谱， 频谱。同样可以画出相位频谱，用以表 kω ψk 随角频率k 示各次谐波的初相 随角频率 ω变动 O 2ω 4ω 6ω 的情形。 的情形。 图 8.3 振幅频谱

非正弦周期电流电路

非正弦周期电流电路
电路与电子学基础
非正弦周期信号及其谐波分析、有效值
f(t)=(4/π)Am(sinωt+1/3sin3ωt+1/5sin5ωt+…)
有效值 F F12 F32 F52
其中
F1 2
2 Am
F3
2
2 Am
3
F5
22 Am5矩形波的幅度频谱非正弦周期电流电路谐波分析法计算步骤:
（1） 分解：利用傅里叶级数展开法，将已知非正弦周期信号 分 解为一系列频率不同、幅值不同、相位不同的正弦分量 之 和，即将非正弦周期函数分解为傅氏级数。
（2） 单独作用：分别计算在各个频率正弦量（即每一个频率 分 量）单独作用下电路中的响应。
（3） 合成：根据线性电路的叠加原理，将所得到的响应分量 的 时域形式叠加，从而求得实际的稳态响应值。
电路与电子学基础

非正弦周期交流电路

非正弦周期交流电路

解 由公式可知，等效正弦电流的有效值为
I ( 0.8)2 (0.25)2 0.593 A
2
2
平均功率为
P
U1I1
cos
1
311 2
0.8 2
cos 85
10.8
W
正弦电压与等效正弦电流之间的相位差为
arc
cos
P UI
arc
cos
10.8 311 0.593
85.2
2
例 方波信号激励的电路。
U0 RI S0
20 78 .5106
1.57 mV
IS0
R u0
2. 基波 作用 is1 100 sin106 t μ A
20Ω R
为了便于分析与计算，通常可将非正弦周期电压和电
流用等效正弦电压和电流来代替。等效的条件是：等
效正弦量的有效值应等于已知非正弦周期量的有效值，
等效正弦量的频率应等于非正弦周期量的基波的频率，
用等效正弦量代替非正弦周期电压和电流后，其功率
必须等于电路的实际功率。这样等效代替之后，就可
以用相量表示。等效正弦电压与电流之间的相位差应
cos
k
d
1 2
[sin(k
0
1)
sin(k
1)]d
1 2
[
cos(k 1) k 1
cos(k 1) k 1
]0
11 k 1 k 1
2 k2 1
即
Ckm
4Um (k2 1)
0
( k为偶数) ( k为奇数)
A0
2Um
Bkm 0
Ckm
4Um (k2 1)
( k为偶数)
可得
k

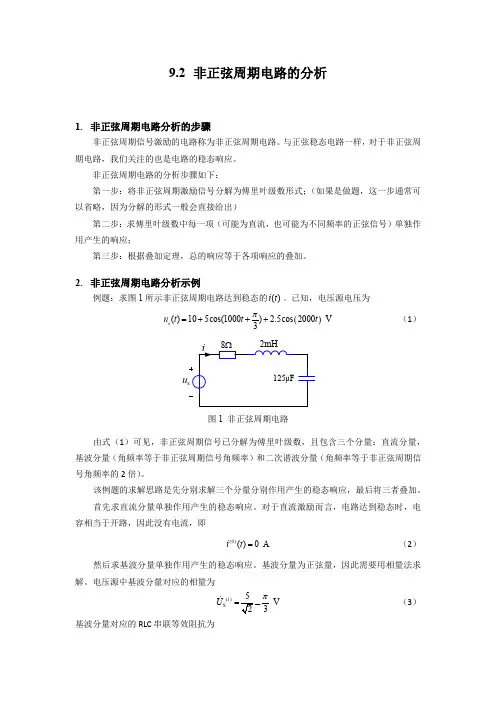
9-2 非正弦周期电路的分析

9-2 非正弦周期电路的分析

U
=(1)
S
基波分量对应的 RLC 串联等效阻抗为
5 ∠π V 23
（3）
Zeq =R
+
jωL
−jBiblioteka ωC=8 +j2
−
j8
=8 −
j6
Ω
根据欧姆定律，可得基波分量单独作用时的电流相量为
（4）
I=(1)
U
(1)
S=
Zeq
2 ∠96.90 A 4
（5）
叠加定理需要在时域中叠加，因此需要将电流相量转换到时域，即
该例题的求解思路是先分别求解三个分量分别作用产生的稳态响应，最后将三者叠加。 首先求直流分量单独作用产生的稳态响应。对于直流激励而言，电路达到稳态时，电 容相当于开路，因此没有电流，即
i(0) (t) = 0 A
（2）
然后求基波分量单独作用产生的稳态响应。基波分量为正弦量，因此需要用相量法求
解。电压源中基波分量对应的相量为
且 Uk = RIk
将式（14）和（15）代入式（13），可得电阻的平均功率为
∞
P = ∑(Ik2R) k =0
由式（16）可得例 1 电路中电阻的平均功率为
1 2
5 2
P=
02
×
8
+
2
×
8
+
16
× 8 ≈ 1.39 W
2
2
（14） （15） （16）
（17）
4. 问与答
问：非正弦周期电路的平均功率定义与正弦稳态电路相同，那么无功功率呢？ 答： 这是一个开放性的问题，迄今尚无统一定义。原因在于非正弦周期电路含有多个频率的 正弦量，而正弦稳态电路中只有一个频率，频率的多样化导致非正弦周期电路难以给出无功 功率的定义。

非正弦周期电路电路的谐波分析法

非正弦周期电路电路的谐波分析法

非正弦周期电路电路的谐波分析法非正弦周期电路通常包含了多个频率的谐波分量。

为了了解电路中每个频率的谐波分量对系统的影响，可以使用谐波分析法进行分析。

谐波分析法的基本思想是将非正弦波形分解为一系列谐波分量，然后分别分析每个谐波分量对电路性能的影响。

谐波分析法中常用的工具是傅里叶级数展开。

任何一个周期函数都可以表示为一系列谐波分量的叠加。

假设输入信号为周期为T的非正弦波形x(t)，则可以用傅里叶级数展开表示为：x(t) = A0 + Σ(Ak*cos(kω0t) + Bk*sin(kω0t))其中，A0为直流分量，Ak和Bk分别为余弦和正弦波的幅值，k为谐波序号，ω0为基频角频率。

谐波分析法的具体步骤如下：1.确定输入或输出信号的周期和基频频率。

2.根据傅里叶级数展开的公式，确定展开式中的直流分量和谐波分量的幅值。

3.通过测量或计算，得到各个傅里叶系数Ak和Bk的值。

4.计算各个谐波分量的幅值和相位，从而得到每个频率的谐波成分的信号波形。

5.根据谐波分量的幅值和相位，分析每个频率的谐波对电路性能的影响。

在实际应用中，谐波分析法可以用于分析非线性电路的谐波失真、功率因数、电压畸变等问题。

例如，对于电力系统中的非线性负载，可以采用谐波分析法来分析电压和电流的谐波含量，从而评估其对电力系统的影响。

此外，谐波分析法也可以应用于音频和音乐信号的处理。

对于复杂的乐器信号，可以通过谐波分析法来分析其频谱成分，以及对音乐声音和声音合成的影响。

在音频合成和虚拟乐器设计中，谐波分析法是一个重要的工具。

总之，非正弦周期电路的谐波分析法是一种用于分析非正弦波形电路的方法，通过将非正弦波形分解为一系列谐波分量来分析电路性能，它在电力系统和音频处理等领域都有广泛的应用。

通过谐波分析法，可以更好地理解非正弦周期电路的特性，从而为电路的设计和优化提供指导。

非正弦周期电路

非正弦周期电路

0
π
2π f（t）sin ktd（t）
0
第4页
A0 a0
非
正
各系数之间的关系应满足：
弦
周
Akm ak2 bk2
k
arctan
ak bk
期 电 路
在分析计算非正弦周期量作用下的线性电路的电流和电压时，可先 将其分解为傅里叶级数，然后根据叠加定理分别计算各分量单独作用
时的电流和电压，最后将计算结果叠加，这一方法称为谐波分析法。
弦
k 1
周
a0 （ak cos kt bk sin kt）
期
k 1
电
a0、ak、傅里叶系数，可按下列各式求得：
路
a0
1 T
T f（t）dt 1
0
2π
2π f（t）d（t）
0
ak
2 T
T f（t）cos ktdt 1
0
π
2π f（t）cos ktd（t）
0
bk
2 T
T f（t）sin ktdt 1
傅里叶级数虽然是一个无穷级数，但在实际应用中，一般根据所需
精度和级数的收敛速度决定所取级数的有限项数。
电 工 电 子 技 术
电
k 1
路
上式中，第一项A0不随时间变化，称为恒定分量或直流分量；第二
项A1msin（ωt＋φ1）的频率与非正弦周期量的频率相同，称为基波或一
次谐波；其余各项的频率为非正弦周期量频率的整数倍，分别称为二
次谐波、三次谐波、…，统称为高次谐波。
第3页
用三角公式展开，上式还可写为另一种形式，即
非
正
（f t） A0 （Akm sin k cos kt Akm cosk sin kt）

非正弦周期电路电路的谐波分析法

非正弦周期电路电路的谐波分析法

1. 前3次谐波分量的叠加波形
2.前5次谐波分量的叠加波形
3. 前11次谐波分量的叠加波形
原理演示
谐波合成方波的演示
1次谐波 3次谐波 5次谐波 7次谐波 1+3次谐波 1+3+5+7次谐波 1+……+49次谐波 原方波信号
T/2
T
1次谐波
返回
T/2
T
3次谐波
返回
T/2
T
5次谐波
返回
K

非正弦周期交流信号的特点 不是正弦波
按周期规律变化
非正弦周期交流信号的分解
f ( t ) A 0
直流分量 二次谐波 （2倍频）
A sin( t f ) 1m 1
基波（和原 函数同频）
A sin( 2 t f ) 2m 2 …..
高次谐波
A0 Akm sin(kt fk )
图3.1
图3.2
表3.1
谐波频率 0 100 200 300 400 500 600 700 800 900 1000 1100 1200 幅度 0.4643 1.9955 0.1395 0.5668 0.0957 0.2949 0.0732 0.1795 0.0570 0.1162 0.0440 0.0772 0.0331 初相位 0.00 -90.00 0.00 -90.02 0.00 -90.04 0.01 -90.06 0.02 -90.08 0.02 -90.110
k 1

周期性方波的分解
直流分量
t
t
三次谐波 五次谐波
基波
t
t
七次谐波
三、实验原理图与仿真结果

周期性非正弦电路分析

周期性非正弦电路分析

雷达信号处理
用于雷达信号的接收、处理和目标识 别。
07
结论与展望
研究成果总结
1 2
周期性非正弦电路分析方法
提出了一种基于傅里叶级数展开的周期性非正弦 电路分析方法，能够准确计算电路的稳态响应和 暂态响应。
电路参数优化
通过优化电路参数，如电阻、电容、电感等，实 现了对周期性非正弦电路性能的优化。
3
非正弦波形生成电路
非正弦波形生成电路是一种能够产生非正弦周期信号的电 路。这种电路通常由振荡器、滤波器和调制器等组成，通 过调整电路参数，可以生成各种非正弦周期信号。
非正弦波形生成电路的优点在于其结构简单、易于实现， 且能够产生多种非正弦周期信号。然而，该方法的缺点在 于其产生的信号精度和稳定性可能较差。
此外，非正弦周期电路的分析方法对于其他复杂电路的分析也具有一定的借鉴意义， 有助于推动电路理论的发展。
02
非正弦周期信号的产生
波形合成法
波形合成法是一种通过组合不同频率的正弦波来生成非正弦 周期信号的方法。通过调整各正弦波的幅度、相位和频率， 可以合成出具有所需特性的非正弦周期信号。
波形合成法的优点在于可以精确控制信号的参数，如频率、 幅度和相位等。此外，该方法还可以生成复杂的非正弦周期 信号，如方波、三角波等。
功率因子校正
为了提高电路的效率，需要对非正弦周期电路进行功率因子校正，以减小无功功率和提高功率因数。
06
非正弦周期电路的应用实例
非正弦电源设计
01
02
03
逆变电源
将直流电转换为交流电， 用于驱动电机、照明等设 备。
脉冲电源
产生高电压、大电流的脉 冲信号，用于焊接、打标 等领域。
开关电源

03-非正弦量及其分析知识点

03-非正弦量及其分析知识点

非正弦周期电路分析
1、基本概念
（1）非正弦周期信号可以用傅里叶级数分解为直流分量和各次谐波分量之和。

其分解式为
）
（）（k 1km 0sin ψωω++=∑∞
=t k A A t f k （2）平均值。

）（t f 的恒定分量A 0就是其平均值
⎰=T
t
t f T A 00d 1）（（3）有效值。

任何非正弦周期交流电流、电压有效值分别为
⋅
⋅⋅+++=222120I I I I ⋅
⋅⋅+++=222120U U U U （4）平均功率。

非正弦交流电路的平均功率等于各次谐波平均功率之和。

⋅
⋅⋅++++=33322211100cos cos cos ϕϕϕI U I U I U I U P 2、分析步骤
非正弦周期信号作用于线性电路时，其分析步骤为：
（1）把给定的非正弦周期电压（或电流）按照傅里叶级数，高次谐波取到哪一项，由计算精度要求决定。

（2）利用叠加原理计算电源的恒定分量和各次谐波分量单独作用时所产生的电流分量。

（3）将所得电流分量叠加起来。

注意：
（1）直流分量（恒定分量）作用于电路时，电容可视为开路，电感可视为短路；
（2）各次谐波作用于电路时，可按照不同频率的正弦交流电路计算。

（3）对于不同频率的正弦量，其感抗和容抗则为
L1Lk kX L k X ==ωC1Ck 11X k
C k X ==ω（4）不同频率谐波分量的代数和不能用相量图或者复数式运算，只能用瞬时值合成。

非正弦周期电流电路

非正弦周期电流电路

非正弦交流电路
非正弦周期电流电路基本的分析方法称为谐波分析法，它是正弦电流电路分析方法的推广。

计算步骤为：首先利用数学中的傅立叶级数，将非正弦周期激励分解成为一系列不同频率的正弦量之和；再根据线性电路的叠加原理，分别计算出各个频率分量单独作用于电路时在电路中产生的响应分量；最后把各响应分量按时域形式进行叠加，就得到了电路在非正弦周期激励下的响应。

若一端口网络端口上的电压、电流表达式为：
1、非正弦计算（一）
分析：由于已给定电压源的付里叶级数展开式，只要按步骤计算出在每一电压分量作用于电路产生的电流响应，再按瞬时值叠加即可。

需要注意的是：直流分量作用电路时，电容相当于开路，正弦分量作用于电路时，随着频率的增高，容抗减小。

方程式及结果如下：
最后将电流叠加并代入功率计算公式：
2、非正弦计算（二）
方程式及结果如下：
3、非正弦计算（三）
分析：若负载中不含基波分量，则电源中基波分量必然降在传输线上，则L、C发生并联谐振；而4ω的谐波分量全部传至负载，要求传输线4ω的谐波阻抗为0；故必须L1、C与L2发生串联谐振，代入串联谐振条件，则电路可解。

方程式及结果如下：。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

有功电流分量和无功电流分量是时间的函数， 由此可得：
1 T 1 T u L (t )iL (t )dt 0 u L (iLP iLQ )dt 0 T T
1 T 1 T 1 T u L (t )iL (t )dt 0 u L (t )iLP (t )dt 0 u L (t )iLQ (t )dt PL 0 0 T T T
3.3.1 单相负载
设交流电的周期为T，则有：
iL
uL(t+T)=uL(t)
iL(t+T)=iL(t)
1 2 电压的有效值为： U L u L dt T 0
T
uL
负 载
电流的有效值为： I L
1 T
T
2 i L dt 0
返 回
上 页
下 页
第三章非正弦周期电路的基本概念
视在功率为：
SL=UL . IL
S P Q D
2 2 2 1
2
返 回
上 页
下 页
第三章非正弦周期电路的基本概念
根据正交特性，可将式 S 2 P 2 Q12 D2 用电压、
电流的形式表达:
U 2 I 2 U 2 (I12 cos2 1 I12 sin 2 1 I2 )
式中，下标表示所有的谐波次数。
T
1 有功功率为： PL iL (t ) uL (t )dt T0
在视在功率、有功功率计算表达式中，有不等式：
b b 2 2 f ( x ) g ( x )d x f ( x )d x g ( x)dx a a a b 2
其相关函数满足：
f ( x) / g ( x) k const
PL 有功电流分量的瞬时表达式为： iLP (t ) 2 u L (t ) UL
无功电流分量的瞬时表达式为：
iLQ (t ) iL (t ) iLP (t )
将有功电流和无功电流分
量的瞬时表达式综合，得弗 莱茨分解原理的图。
UL
IL ILQ ILP
1/G
返 回
上 页
下 页
第三章非正弦周期电路的基本概念
返回 下 页
第三章非正弦周期电路的基本概念 1 i1 交流电网 U1N U2N n U3N
若将系统中的一点选为参
考点，并令该参考点为“0”， 则图中负载吸收的有功功率 为：
T T
2 i2
3 i3
T
1 1 1 PL0 u10 (t ) i1 (t )dt u20 (t ) i2 (t )dt u30 (t ) i3 (t )dt T0 T0 T0

基波电流含有率为：
g=I1/I×100%
谐波电流含有率为： k
I
h2

2 h
I
100%
谐波电流和总功率因数的关系为：
I k I
g cos1
返 回 上 页 下 页
IL
1 2 iL d t T 0
T
第三章非正弦周期电路的基本概念
3.3 似稳态过程计算中应注意的几个问题
任何多相系统各变量之间的关系都可以用三相系统 T 1 进行描述。根据方程 PL u L (t ) iL (t )dt 计算各 T 0 部分有功功率之和，即：
P um0 (t ) im (t ) dt
m1 0 3 T
式中，“0”表示参考点；“m”表示相的符号。
三相三线制系统（零系统）有：
此时，功率因数可表示为：
PL / SL
（其值始终小于或等于1）
返 回
上 页
下 页
第三章非正弦周期电路的基本概念
根据费莱茨电流分解法，谐波存在时，电流iL(t)可 分解为有功和无功两个电流分量，即：
iL (t ) iLP (t ) iLQ (t )
iLp(t)：有功电流分量； iLQ(t)：无功电流分量，
总是保持各分量相互正交。基波无功电流分量为：
iLQ 1
QL1 导纳Y为： Y 2 U L1
T Yu L1 (t ) 4
1 T T 基波无功功率分量QL1为： QL1 0 u L1 (t )iL (t )dt T 4
返 回 上 页 下 页
第三章非正弦周期电路的基本概念
无功电流分量是一个正弦波，与基波电压分量相差 90，与前所述各种电流分量相互正交，因此， 基波的无功功率为：
第三章非正弦周期电路的基本概念
有功功率
传输功率的平均值 星形 连接
1 i1 U1N U2N n U3N
T
1 T PL 0 u L (t ) iL (t )dt T
负载吸收的有功
功率为:
T T
交流电网
2 i2
3 i3
1 1 1 PL u1N (t ) i1 (t ) dt u2 N (t ) i2 (t ) dt u3 N (t ) i3 (t ) dt T0 T0 T0
iLP (t ) GuL (t )
G：
电导
T 1 T 2 2 u L (t )iL (t )dt Gu L (t )dt GU L 0 T 0
返 回 上 页 下 页
G 的选择满足有功电流分量可传递的全部有功功率：
第三章非正弦周期电路的基本概念
PL 电导G可为： G 2 UL
但此时的电压、电流并不为理想的正弦波，而是周 期性的非正弦。 “似稳态”过 程 电力电子技术的应用中非 正弦的稳态运行过程。
返 回
上 页
下 页
第三章非正弦周期电路的基本概念
交流系统的电压可近似认为是理想的正弦波，电流 可认为是畸变波，用U表示理想的正弦波电压，用下
标“1”表示周期性畸变电流基波分量，则前面的有
返 回
上 页
下 页
第三章非正弦周期电路的基本概念
b b 2 2 f ( x ) g ( x )d x f ( x )d x g ( x)dx a a a b 2
将电压、电流有效值和视在功率带入上式中可得：
PL S L
PL S L
(当 uL (t ) / iL (t ) k 时，即无相位差时)
P U I cos
三相对称系统
2 视在功率
P 3 U I cos
S U I
单相系统
三相对称系统
S 3 U I
返 回 上 页 下 页
第三章非正弦周期电路的基本概念
3 无功功率
单相系统
三相对称系统
Q U I sin
Q 3 U I sin
返 回
上 页
下 页
第三章非正弦周期电路的基本概念
函数互为正交 n个周期函数f1(t)，， fn(t)，当满足下列条件：

t T
t
ik 0 fi (t ) f 2 P 2 Q12 所表示的各功率之间互 为正交，故其表达式也可以转换为：
系统参考点可以是任何一点，如将端点3作为参考点， 则有：
T T 1 PL u13 (t ) i1 (t ) dt u23 (t ) i2 (t ) dt T 0 0
返 回
上 页
下 页
第三章非正弦周期电路的基本概念
3.1 正弦稳态过程的功率定义
1 有功功率 单相系统
返 回
上 页
下 页
第三章非正弦周期电路的基本概念
1 1 1 PL0 u10 (t ) i1 (t )dt u20 (t ) i2 (t )dt u30 (t ) i3 (t )dt T0 T0 T0
将上式进行分解后得：
T T T 1 PL 0 u1N (t ) u N 0 (t ) i1 (t )dt u2 N (t ) u N 0 (t ) i2 (t )dt u3 N (t ) u N 0 (t ) i3 (t )dt T 0 0 0
返 回
上 页
下 页
第三章非正弦周期电路的基本概念
根据基尔霍夫电流定律，网络流向负载的三个电流之 和为零，PL = PL0，即
T T T 1 PL u10 (t ) i1 dt u 20 (t ) i2 (t ) dt u30 (t ) i3 (t ) dt T 0 0 0
P cos 4 功率因数 S 三种功率之间的关系为： S2=P2+Q2
以上表达式中，U和I分别表示线电压和线电流；
表示线电压和线电流之间的相位差。
返 回 上 页 下 页
第三章非正弦周期电路的基本概念
3.2 正弦电压源激励下的似稳态过程
电力电子技术的应用中，即使在周期性的电子开关
作用下，系统中的电压、电流处于稳定运行状态，
T
T
T
T T T T 1 u1N (t ) i1 (t ) dt u2 N (t ) i2 (t ) dt u3 N (t ) i3 (t ) dt u N 0 (t ) (i1 i2 i3 ) dt T 0 0 0 0
式中：
1 T u L (t )iLQ (t ) dt 0 T 0
uL与iLQ相互正交，因此iLp与iLQ也相互正交。
返 回
上 页
下 页
第三章非正弦周期电路的基本概念
根据前面各公式的基本概念可知：
2 T T 1 1 2 2 IL 0 iL (t )dt 0 iLP (t ) iLQ (t ) dt T T 1 T 2 1 T 2 2 T 2 I L 0 iLP (t )dt 0 iLQ (t )dt 0 iLP (t )iLQ (t )dt T T T 根据正交性原理，上式的最后一项为零，因此：