当前位置：文档之家 › 非正弦周期电流电路及电路频率特性

非正弦周期电流电路及电路频率特性

  • 格式：doc
  • 大小：35.00 KB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

电路原理课件10非正弦周期电流电路

电路原理课件10非正弦周期电流电路

返回 上页 下页
非正弦周期电流电路 工程上傅里叶级数常用另一种形式：
f ( t ) = A0 + A1mcos(1t + 1 ) + = A0 + Akm cos( k1t + k )
k =1
= a0 + [ak cos( k1t ) + bk sin( k1t )]
交流稳态分析
暂态分析
返回 上页 下页
非正弦周期电流电路
返回 上页 下页
非正弦周期电流电路 用晶体管特性图示器测 量晶体二极管的电压电流关 系。
实验表明： 在低频工作条件下，晶
体二极管的电压电流关系是
u-i 平面上通过坐标原点的 一条曲线。
返回 上页 下页
非正弦周期电流电路
返回 上页 下页
非正弦周期电流电路
f ( t ) = a0 + [ak cos( k1t ) + bk sin( k1t )] k =1 因 bk = 0 f ( t ) = a + [a cos( k t ) b sin( k t )] 0 k 1 k 1 k =1 a k = 0 2. 奇函数： f (t) = f (t)，有 a0 = 0
返回 上页 下页
非正弦周期电流电路
10.1 非正弦周期信号的谐波分析
一、非正弦周期函数分解为傅里叶(Fourier)级数 满足狄里赫利条件的周期函数 f(t) = f(t + kT)[式中T 为周期函数 f(t)
的周期，k = 0，1，…]，可展开为收敛的傅里叶级数：
f ( t ) = a0 + [a1cos(1t ) + b1sin(1t )] + [a2cos(21t ) + b2sin(21t )] + + [ak cos( k1t ) + bk sin( k1t )] + = a0 + [ak cos( k1t ) + bk sin( k1t )]

非正弦周期电流电路及电路频率特性

非正弦周期电流电路及电路频率特性
电压分配
电感与电容两端的电压相等且相位相反，总电压 等于电阻两端的电压。
阻抗最小
在谐振频率下，电路的阻抗达到最小值，使得电 流达到最大值。
品质因数
串联谐振电路的品质因数Q较高，表示电路的选 择性较好。
并联谐振条件及特点
并联谐振条件
阻抗最大
电流分配
品质因数
在RLC并联电路中，当电源频 率等于电路的固有频率时，电 路发生并联谐振。此时，电路 中的阻抗最大，电流最小，且 电感与电容支路的电流相等且 相位相反。
电路频率特性的研究
探讨非正弦周期电流电路在不同频率下的响应特性，包括幅频特性、 相频特性和阻抗特性等，并分析这些特性对电路性能的影响。
实际应用案例
结合具体实例，展示非正弦周期电流电路及其频率特性在实际应用中 的价值，如电力电子设备、通信系统和控制系统等。
02
非正弦周期电流电路基本概 念
非正弦周期信号定义
非正弦周期信号
与正弦信号不同，非正弦周期信号的 波形在一个周期内不能简单地用正弦 函数描述。这种信号可以分解为一系 列不同频率的正弦波分量。
周期与非周期信号
周期信号是指在一个固定时间间隔内 重复出现的信号，而非周期信号则不 具有这种重复性。非正弦周期信号属 于周期信号的一种。
傅里叶级数展开与频谱分析
通频带
对于具有一定带宽的信号而言，能够通过谐振电路并被放大的频率范围称为通频带。通频带的宽度与 电路的品质因数Q有关，Q值越高则通频带越窄，反之则越宽。在实际应用中，需要根据信号的特点 和电路的要求来选择合适的通频带宽度。
06
非正弦周期电流电路实验验 证与仿真分析
实验目的和步骤
01
实验目的：通过搭建非正弦周期电流电路，验证其工作原 理和特性，并利用仿真软件进行分析，深入理解电路的频 率响应。

非正弦周期性电流电路

非正弦周期性电流电路

增加能耗
非正弦周期性电流可能导致额外的 能耗，增加能源消耗和运营成本。
非正弦周期性电流的消除方法
电路中加入滤波器可以 滤除非正弦周期性电流成 分。
优化电源设计
优化电源设计，提高电源 的输出质量，减少非正弦 周期性电流的产生。
采用线性负载
采用线性负载可以减少谐 波干扰和非正弦周期性电 流的影响。
非正弦周期性电流电 路
目录
• 非正弦周期性电流电路概述 • 非正弦周期性电流的产生与影响 • 非正弦周期性电流电路的分析方法
目录
• 非正弦周期性电流电路的实验研究 • 非正弦周期性电流电路的工程应用 • 非正弦周期性电流电路的发展趋势与展望
01
非正弦周期性电流电路概 述
定义与特点
特点
定义：非正弦周期性电流电 路是指电路中的电流呈非正
在控制系统中的应用
执行器控制
非正弦周期性电流电路可以用于执行器的控制，以实现系统的稳 定性和动态性能。
传感器信号处理
非正弦周期性电流电路可以用于传感器信号的处理，以提取有用 的信息并进行反馈控制。
伺服系统
非正弦周期性电流电路可以用于伺服系统的设计，以实现精确的 位置和速度控制。
06
非正弦周期性电流电路的 发展趋势与展望
如雷电、电磁场等外部因素可能对电 路产生干扰，导致非正弦周期性电流 的产生。
电路中元件的非线性
电路中的元件，如电阻、电容、电感 等，可能具有非线性特性，导致非正 弦周期性电流的产生。
非正弦周期性电流对电路的影响
电压波动
非正弦周期性电流可能导致电压 波动，影响用电设备的正常运行。
谐波干扰
非正弦周期性电流可能产生谐波干 扰，影响通信和信号处理设备的性 能。

非正弦周期电流电路

非正弦周期电流电路

第9章非正弦周期电流电路电子技术中广泛使用着非正弦周期信号，例如脉冲信号发生器、锯齿波发生器等。

本章首先介绍了非正弦周期量产生的原因，其次讲述了非正弦周期信号的分解与合成，在此基础上对非正弦周期信号进行了谐波分析；介绍了非正弦周期信号的频谱表示法及频谱的特点；最后对非正弦周期信号作用下线性电路的分析计算进行了研究。

本章的学习重点：●非正弦周期信号的谐波分析法；●非正弦周期信号的频谱分析法；●非正弦周期信号作用下线性电路的分析与计算。

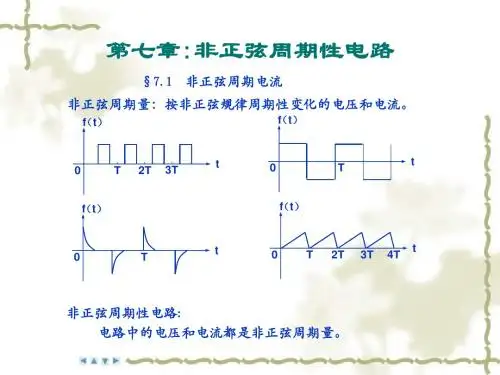
9．1 非正弦周期信号1、学习指导（1）非正弦周期信号的产生当电路中激励是非正弦周期信号时，电路中的响应也是非正弦的；当不同波形的周期信号加到电路中，在电路中产生的电压和电流当然也是非正弦波；若一个电路中同时有几个不同频率的正弦激励共同作用，电路中的响应一般也是非正弦量；电路中含有非线性元件时，即使激励是正弦量，电路中的响应也可能是非正弦周期函数。

非正弦周期信号的波形变化具有周期性，这是它们的共同特点。

（2）非正弦周期信号的合成与分解电子技术工程中大量使用着非正弦周期信号，当几个不同频率的正弦波合成时，其合成的结果是一个非正弦波，受此分析结果的启发，设想一个非正弦周期信号也一定可以分解为一系列的振幅不同、频率成整数倍的正弦波，由此引入了利用傅里叶级数表示非正弦周期信号的分析方法。

2、学习检验结果解析（1）电路中产生非正弦周期波的原因是什么？试举例说明。

解析：电路中产生非正弦周期波的原因一般有以下几个方面：①当电路中激励是非正弦周期信号时，电路中的响应当然也是非正弦的。

例如实验设备中的函数信号发生器，其中的方波和等腰三角波，它们在电路中产生的电压和电流不再是正弦的；123②同一电路中同时作用几个不同频率的正弦激励时，电路中的响应一般不再是正弦的。

例如晶体管放大电路，它工作时既有为静态工作点提供能量的直流电源，又有需要传输和放大的正弦输入信号，在它们的共同作用下，放大电路中的电压和电流既不是直流，也不是正弦交流，而是二者相叠加以后的非正弦波；③当电路中含有非线性元件时，即使激励是正弦量，电路中的响应也可能是非正弦周期函数。

第十二章 非正弦周期电流电路

第十二章 非正弦周期电流电路
IS 0
is1
is3
华东理工大学 上 页 下
页
§12-3 有效值、平均值和平均功率
一. 有效值
根据周期量有效值的定义, 为其方均根值:
I
1 T
0
T
[it ] dt U
2
1 T
0
T
[u t ]2 dt
it I 0 I km cos(k1t k )
k 1
P U 0 I 0 U k I k cos k
k 1

（三角函数的正交性）
U 0 I 0 U 1 I1 cos1 U 2 I 2 cos 2 U k I k cos k
Um Im 式中 : U k , Ik , k uk ik , k 1,2, 华东理工大学 2 2
0
ui
t
+ uo
③非正弦激励下的线性电路
0
－
+
0
t
ui
t
uo
0
t
页
－ 华东理工大学 上 页 下
§12-2 周期函数分解为傅里叶级数 (谐波分析) 一. 数学分析
设非正弦周期电流i(t)=i(t+T) ,当满足狄里赫利条件 ( ① i(t)在一周期内连续or有有限多个第一类间断点; ② i(t)在一周期内有有限多个极大值与极小值 )时, 可展成收敛的傅里叶级数：
I av
1 T i dt 0 T
例：正弦电流的平均值 为 1 T 2 I av 0 I m cost dt I M 0.898 I M 0.637 I T 恒定分量（直流分量） 磁电系仪表：
电磁系仪表： 全波整流仪表：

非正弦周期信号电路

非正弦周期信号电路
瞬态分析主要采用时域分析方法，通过建立电路的微分方程或差分方程来求解。
瞬态分析的目的是了解电路在非正弦周期信号作用下的动态响应过程，包括电压、 电流的峰值、相位、波形等参数。
稳态分析
稳态分析是研究非正弦周期信号作用于电路时，电路 达到稳态后电压和电流的平均值或有效值。
稳态分析主要采用频域分析方法，通过将非正弦周期 信号进行傅里叶级数展开，转化为多个正弦波成分，
非正弦周期信号电路可以用于设计音频功率 放大器，将微弱的音频信号放大到足够的功 率以驱动扬声器或其他音频输出设备。
电力电子系统
逆变器
01
非正弦周期信号电路可以用于设计逆变器，将直流电转换为交
流电，以驱动电机、照明和加热等设备。
整流器
02
非正弦周期信号电路也可以用于设计整流器，将交流电转换为
直流电，以提供稳定的直流电源。
再对每个正弦波成分进行单独分析。
稳态分析的目的是了解电路在非正弦周期信号作用下 的稳态工作状态，包括平均功率、效率等参数。
频率响应分析
1
频率响应分析是研究非正弦周期信号作用于电路 时，电路在不同频率下的响应特性。
2
频率响应分析主要采用频域分析方法，通过测量 电路在不同频率下的输入输出特性，绘制频率响 应曲线。
生物医学工程
在生物医学工程中，非正 弦周期信号用于刺激或记 录生物体的电生理信号。
02
非正弦周期信号电路的基本 元件
电感元件
电感元件是利用电磁感应原理制 成的元件，其基本特性是阻碍电
流的变化。
当电感元件的电流发生变化时， 会在其周围产生磁场，储存磁场
能量。
电感元件的感抗与频率成正比， 因此对于非正弦周期信号，电感 元件会对其产生较大的阻碍作用。

电子技术课件_非正弦周期电流电路

电子技术课件_非正弦周期电流电路
第五章
非正弦周期电流电路
第五章 非正弦周期电流电路
概述
§5.1. 非正弦周期量的分解 §5.2. 非正弦周期量的有效值 §5.3. 非正弦周期量的计算
§5.3. 非正弦周期电流电路中 的平均功率
概述
非正弦周期交流信号的特点：
不是正弦波 按周期规律变化
半波整流电路的输出信号：
非正弦周期交流信号
f (wt ) = A0 + Bkm sin kwt + Ckm coskwt
k =1 k =1


f (wt ) = A0 + Bkm sin kwt + Ckm coskwt
k =1 k =1


1 2 教材p174 A0 = f ( w t ) d ( w t ) (5.1.5)式 2 0 1 2 Bkm = f (w t ) sin kw td (w t )
① ② 式联立求解得： L=0.01H
② C=100µ F
1 2000L 0 2000 C arctg = 20 + R =36.30
P=P1 + P2 + U1I1COS 1+U2I2COS2 = 538.4W
例2 方波信号激励的电路
iS
Im
T/2 T
R
t
iS
C
u
L
已知： R
= 20、 L = 1mH、C = 1000 pF I m = 157 μ A、 T = 6.28S
直流分量
级数
基波（和原 函数同频）
+ …..
= A0 + Akm sin(kwt + fk )
k =1

电气学院《电路-非正弦周期电流电路和信号的频谱》课件

电气学院《电路-非正弦周期电流电路和信号的频谱》课件

k =1
例 周期性方波 的分解
直流分量 t
三次谐波
t
基波 t
五次谐波 七次谐波 t
直流分量+基波 直流分量 基波
直流分量+基波+三次谐波
三次谐波
频谱图
时域
U
Um
T
t
4U m
=U0
U0
3
w 3w
频域
U0
5w
5w
U = 4Um (coswt + 1 cos 3wt + 1 cos 5wt + )
π
13-4 非正弦周期电流电路的计算
一、一般步骤：
1） 将激励为非正弦周期函数展开为傅立叶级数： f (w t) = A0 + Ak m cos(kw t + k ) k =1 2） 将激励分解为直流分量和无穷多个不同频率的 正弦激励分量； 3） 求各激励分量单独作用时的响应分量：
(1) 直流分量作用：直流分析（C开路，L短路）求Y0;
（2）基波分量作用：角频率为w （正弦稳态分析）求y1; （3）二次谐波分量作用：角频率为2w （正弦稳态分析）求y2;
………………
4) 时域叠加：y(t)= Y0 + y1 + y2 + y3 + y4 + ……
例：图示电路中 us (t) = 40 + 180 coswt + 60 cos(3wt + 45)
二、非正弦周期函数的有效值
若 u(wt) = U0 + Ukm cos(kwt + k ) k =1
则： U =
U
2 0
+ U12
+

非正弦周期电流电路分析

非正弦周期电流电路分析

非正弦周期电流电路分析简介非正弦周期电流电路是一种电路，其中电流的波形不是正弦曲线。

这种电路通常由非线性元件或者非理想元件构成，导致电流波形发生变化。

本文将对非正弦周期电流电路进行分析，探讨其中的特点和应用。

非正弦周期电流的产生非正弦周期电流可以由多种方式产生，包括以下几种常见情况：1.非线性元件的非线性特性导致电流波形变化。

例如，二极管在反向偏置时会产生非线性特性，导致电流波形不是正弦曲线。

2.非理想元件的特性导致电流波形变化。

例如，电感元件的饱和和饱和恢复会导致电流波形非正弦。

3.控制信号或输入信号的特性导致电流波形变化。

例如，方波、脉冲或其他非正弦的控制信号输入到电路中时，会引起电流波形的变化。

非正弦周期电流的特点非正弦周期电流具有以下几个特点：1.波形失真：由于非线性元件或非理想元件的特性，非正弦周期电流的波形会失真。

这种失真包括高次谐波的增加或者波形畸变。

2.频谱分布：非正弦周期电流的频谱分布比正弦电流更加复杂。

由于波形的非线性和不规则，频谱中会包含多个谐波成分。

3.能量损耗：非正弦周期电流的能量损耗比正弦电流更大。

由于电流波形的非正弦特性，导致电路中存在额外的损耗。

4.信号干扰：非正弦周期电流会产生更多的信号干扰。

由于频谱中存在多个谐波成分，这些谐波会干扰其他电路或设备的正常运行。

非正弦周期电流电路分析方法对于非正弦周期电流电路的分析，可以采用以下方法：1.线性电路分析：首先将非正弦周期电流分解为多个谐波成分，然后对每个谐波成分进行线性电路分析。

通过将各个谐波成分的响应叠加，可以得到整个非正弦周期电流电路的响应。

2.时域分析：使用时域分析方法，通过观察电流波形的变化来理解非正弦周期电流电路的工作情况。

这种方法适用于简单的电路，可以直接观察电流波形的特点。

3.频域分析：使用频域分析方法，对非正弦周期电流的频谱进行分析。

通过观察频谱中的谐波成分，可以了解电流波形的非正弦特性。

4.仿真分析：使用电路仿真软件，对非正弦周期电流电路进行仿真分析。

第七章非正弦周期性电路概要

第七章非正弦周期性电路概要

f(t)
t
0
0
例题
已知周期函数f（t）如图所示，求其傅立叶级数的展开式。
Am
－T
f(t)
f（t）既是偶函数（ bK=0）
T 2
0
－Am
T
t
又是奇谐波函数（ aK=0，不含偶次谐波）
T T 4 T 4 A 1 m 4 2 a K 2 f ( t ) cos(kt )dt sin( k t ) sin( k t ) 0 T 0 T T k 4 T 4A 4A m T k 4 2 m cos( k t ) dt cos( k t ) dt sin T T 0 k 2 4
解
2 2 U U0 U1 U2 2
180 60 2 40 140V 2 2
2
2
非正弦周期电流电路中的有效值和有功功率
二、平均值 非正弦周期量的平均值是它的直流分量
整流平均值 上下半周对称的电流
I rect
1 T i dt T 0 2 T I rect 2 i dt T 0
1 T U0 U km sin(kt ku ) I0 I km sin(kt ki )dt T 0 k 1 k 1
1 T 1 T P pdt uidt T 0 T 0
非正弦周期电流电路的有效值和有功功率
4. 周期函数为奇谐波函数 满足f（t）=－f（t + 对称于横轴。 表示为

a0 f ( t ) a K cos(kt ) 2 k 1
T 2
），波形移动半个周期后与原函数波形 k为奇数

非正弦周期电路

非正弦周期电路

0
π
2π f（t）sin ktd（t）
0
第4页
A0 a0
非
正
各系数之间的关系应满足：
弦
周
Akm ak2 bk2
k
arctan
ak bk
期 电 路
在分析计算非正弦周期量作用下的线性电路的电流和电压时，可先 将其分解为傅里叶级数，然后根据叠加定理分别计算各分量单独作用
时的电流和电压，最后将计算结果叠加，这一方法称为谐波分析法。
弦
k 1
周
a0 （ak cos kt bk sin kt）
期
k 1
电
a0、ak、傅里叶系数，可按下列各式求得：
路
a0
1 T
T f（t）dt 1
0
2π
2π f（t）d（t）
0
ak
2 T
T f（t）cos ktdt 1
0
π
2π f（t）cos ktd（t）
0
bk
2 T
T f（t）sin ktdt 1
傅里叶级数虽然是一个无穷级数，但在实际应用中，一般根据所需
精度和级数的收敛速度决定所取级数的有限项数。
电 工 电 子 技 术
电
k 1
路
上式中，第一项A0不随时间变化，称为恒定分量或直流分量；第二
项A1msin（ωt＋φ1）的频率与非正弦周期量的频率相同，称为基波或一
次谐波；其余各项的频率为非正弦周期量频率的整数倍，分别称为二
次谐波、三次谐波、…，统称为高次谐波。
第3页
用三角公式展开，上式还可写为另一种形式，即
非
正
（f t） A0 （Akm sin k cos kt Akm cosk sin kt）

第7章 非正弦周期电流电路

第7章 非正弦周期电流电路

第七章 非正弦周期电流电路
7. 3 非正弦周期电流电路的计算 非正弦周期性电流电路的分析计算方法,主要是利用傅 里叶级数将激励信号分解成恒定分量和不同频率的正弦量之 和,然后分别计算恒定分量和各频率正弦量单独作用下电路 的响应,最后利用线性电路的叠加原理,就可以得到电路的实 际响应。这种分析电路的方法称谐波分析法。其分析电路的 一般步骤如下: (1 )将给定的非正弦激励信号分解为傅里叶级数,并根据 计算精度要求,取有限项高次谐波。
第七章 非正弦周期电流电路Fra bibliotek对上例的正弦量
对于同一非正弦周期电流,当我们用不同类型的仪表进 行测量时,往往会有不同的结果。如用磁电系仪表测量时,所 得结果为电流的恒定分量;用电磁系或电动系仪表测量时,所 得结果将是电流的有效值;用全波整流磁电系仪表测量时,所 得结果将是电流的平均值,但标尺按正弦量的有效值与整流 平值的关系换算成有效值刻度,只有在测量正弦量时读数为 其实际有效值,而测量非正弦量时会有误差。
第七章 非正弦周期电流电路
表 7.1 中,三角波、梯形波、锯形波都是奇谐波函数。 交流发电机所产生的电压实际为非正弦周期性的电压(一般 为平顶波),也属于奇谐波函数。 可以证明,奇谐波函数的傅里 叶展开式中只含有奇次谐波, 而不含直流分量和偶次谐波, 可表示为
第七章 非正弦周期电流电路
函数对称于坐标原点或纵轴,除与函数自身有关外,与计 时起点也有关。而函数对称于横轴,只与函数本身有关,与计 时起点的选择无关。因此,对某些奇谐波函数,合理地选择计 时起点,可使它又是奇函数或又是偶函数,从而使函数的分解 得以简化。如表 7.1 中的三角波、矩形波、梯形波,它们本身 是奇谐波函数,其傅里叶级数中只含奇次谐波,如表中选择的 计时起点,则它们又是奇函数,不含余弦项,所以,这些函数的傅 里叶级数中只含有奇次正弦项。

电工学课件第5章-非正弦周期电流的电路

电工学课件第5章-非正弦周期电流的电路

5.2 非正弦周期量的有效值
一、平均值
若
u U0 U km sin(kwt k )
k 1
则其平均值为： (直流分量)
U AV
1
2
02 udwt
U0
平均值
面积 周期
二，有效值
若 i I0 Ikm sin(kwt k )
k 1 则有效值:
I 1 T i2dt
T0
1 T
T 0
I0
WA i
u
R
求（1）电流的瞬时表达式;
（2） A 、V 的读数； V
（3） W 的读数.
解: I1 U1 4A
R
I 3 U 3 3A R
i1 4 2 sin(wt 30o )A i3 3 2 sin(3wt 60o )A
电流i的瞬时表达式 i 4 2 sin(wt 30o ) 3 2 sin(3wt 60o )A
o
t
T
5.1 非正弦周期量的分解
i e1 E0
e e1
E0
0
已知E0为直流电源, e1为正弦信号源
该电路总电动势为
R e E0 e1 E0 E1m sinw t
其波形如图所示,显然不是正弦量 电路中的电流也不是正弦量
E1m
i e E0 E1m Sinwt
RR R
wt
由此题可知:
直流电量+正弦交流电量=非正弦周期电量
第5章 非正弦周期电流的电路
目录
5.1 非正弦周期量的分解 5.2 非正弦周期量的有效值 5.3 非正弦周期电流的线性电路的计算 5.4 非正弦周期电流电路中的平均功率
概述
一. 非正弦周期交流信号的特点
不是正弦波 按周期规律变化

电路理论第十三章 非正弦周期电流电路和信号的频谱

电路理论第十三章 非正弦周期电流电路和信号的频谱

周期性非正弦信号 相量分析法
傅里叶级数展开 计算单独作用
一系列不同频率的正弦
叠加
全响应
§13.2周期函数分解为傅里叶级数
设周期函数f (t)，周期为T ，则有 f (t) f (t kT)
(k为任意整数）
如果f (t) 满足狄里赫利条件，则 f (t)就能展开成一个
收敛的傅里叶级数（本书中均满足）。即有：
（电压）的绝对值的平均值。
正弦电流的平均值为：I av
1 T
T
0
Im
cost dt
4Im T
T 4
costdt
0
4Im T
[1
T
sin t]0 4
0.637I m
0.898I
相当于正弦电流经全波整流后的平均值。
3.平均功率：任意一端口的瞬时功率为：
p ui [U0 U km cos(k1t uk )][I0 Ikm cos(k1t ik )]
Ik2
k 1
k 0
即非正弦周期电流的有效值等于恒定分量的平方
与各次谐波有效值的平方之和的平方根。
同样也适用于非正弦周期的电压，即有：
U U02 U12 U22
2.平均值：
U 02 U k 2 k 1
Uk 2
k 0
Iav
1 T
T 0
i dt
或
U av
1 T
T 0
u dt
即非正弦周期电流（电压）的平均值等于此电流
1
41L1
41L2
41C1
从而可得：
j 41 L2
1 1
41L1
0
+ us (t) _
L1
L2

第10章 非正弦周期电流电路

第10章 非正弦周期电流电路

P0 P1 P2 ......
平均功率＝直流分量的功率＋各次谐波的平均功率
平均功率只取决于电阻，与电容和电感无关，又有
P I 2R I02R I12R I22R Ik2R
注意
1. 只有同频率的电压谐波和电流谐波才能构成平均功率。 非同频率的平均功率为零。
10.3 有效值、平均值和平均功率
非正弦周期函数的有效值

若 i(t ) I0 Ikmcos(kω1t ψk )
则有效值:
k 1
I 1 T i2dt
T0
1 T
T

2
0
I0

Ikmcos kω1t
k 1
ψk
dt
I
I
2 0

1 2
10.2 非正弦周期函数分解为傅里叶级数
非正弦周期函数的频谱
由于只要求得各谐波分量的振幅和初相，就可确定一个函数
的傅里叶级数。在电路中为了直观地表示，常用频谱图表示。 频谱——描述各谐波分量振幅和相位随频率变化的图形称为
频谱图或频谱。
1. 幅度频谱：f(t)展开式中Akm与 (=k 1)的关系。反映了各频率成份
2. 电路中产生非 正弦周期波的原 因是什么？试举 例说明。
3. 有人说：“只要 电源是正弦的，电 路中各部分的响应 也一定是正弦波” ，这种说法对吗？ 为什么？
4. 试述谐波分析法 的应用范围和应用 步骤。
10.2 非正弦周期函数分解为傅里叶级数
周期函数 f(t) = f(t+kT) (k = 1, 2, 3, …) 若满足狄里赫利条件
非正弦 周期量 (激励)
不同频率 正弦量的和

电路分析 第九章 非正弦周期电流电路

电路分析 第九章 非正弦周期电流电路

第九章 非正弦周期电流电路9.1 非正弦周期信号非正弦周期激励−−−−→傅里叶级数一系列不同频率的正弦量及恒定分量之和−−−−−−→线性电路叠加定理各个正弦量及恒定分量单独作用下在电路中产生的同频正弦电流分量和电压分量−−−−→时域叠加电路在非正弦周期激励下的稳态电流和电压。

谐波分析法的实质：把非正弦周期电流电路的计算化为一系列正弦电流电路的计算和直流电流电路的计算。

9.1.1 周期函数分解为傅里叶级数任一周期性函数()()f t f t kT =+，只要满足狄里赫利条件，都可以分解为一个收敛的傅里叶级数。

0111011()[cos()sin()]cos()k k k km k k f t a a k t b k t A A k t ωωωϕ∞=∞==++=++∑∑其中：00,cos ,sin ,arctan kkm k km k k km k k k b A a A a A b A a ϕϕϕ⎛⎫-====-= ⎪⎝⎭. 上式中的每一项，称为正弦谐波分量，简称谐波。

常数0A 称为零次谐波（直流分量），111cos()m A t ωϕ+称为一次谐波，或基波。

上式中的系数，可按下列公式计算：20211()d ()d TT T o a f t t f t t T T -==⎰⎰π1110π21()cos()d ()cos()d()πT k a f t k t t f t k t t T ωωω-==⎰⎰ π1110π21()sin()d ()sin()d()πT k b f t k t t f t k t t T ωωω-==⎰⎰9.1.2 非正弦周期量的频谱傅里叶级数中各次谐波的振幅与初相可以用图形直观地显示，称为频谱图。

幅值频谱：表示振幅的图形。

横轴表示角频率，纵轴表示谐波振幅。

初相频谱：表示初相的图形。

用直线段分别表示各次谐波的初相。

周期性非正弦量的频谱是离散的。

9.2 波形对称性与傅里叶级数的关系根据波形对称性可知傅里叶级数的某些分量为0，可简化计算。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

非正弦周期电流电路及电路频率特性 4.5 三相电路的功率 4.5 三相电路的功率例题3 第5章电路的频率特性非正弦周期交流电路非正弦周期交流电路非正弦周期交流电路 5.1 非正弦周期交流电路的分析和计算 1. 非正弦周期信号 1. 非正弦周期信号 1. 非正弦周期信号 2. 非正弦周期电流电路分析 2. 非正弦周期电流电路分析 2. 非正弦周期电流电路分析 2. 非正弦周期电流电路分析2. 非正弦周期电流电路分析 3. 非正弦周期量的有效值 3. 非正弦周期量的有效值 3. 非正弦周期量的有效值 4. 非正弦周期电流电路的平均功率 4. 非正弦周期电流电路的平均功率 4. 非正弦周期电流电路的平均功率 4. 非正弦周期电流电路的平均功率 4. 非正弦周期电流电路的平均功率 4. 非正弦周期电流电路的平均功率习题 5.2 RC串联电路的频率特性 5.2 RC串联电路的频率特性 5.2 RC 串联电路的频率特性 5.2 RC串联电路的频率特性 5.3 RC串/并联电路的频率特性 5.3 RC串/并联电路的频率特性 5.3 RC串/并联电路的频率特性谐振的概念串联谐振特点串联谐振特点串联谐振特点串联谐振特点串联谐振特点串联谐振特点串联谐振特点串联电路频率特性阻抗的幅频特性阻抗的相频特性电流的幅频特性电流的幅频特性电流抑制比谐振通用曲线谐振通用曲线5.5 LC并联电路的频率特性例题1 例题2 例题3 例题3 例题3 例题3 例题3 例题4 R + _ + _ . . + _ . . 网络函数：响应相量激励相量―幅频特性―相频特性 R + _ + _ . . + _ . . 0 ω1/RC 相频特性 RC低通滤波器：带宽：截止角频率幅频特性 0 ω1 0.707 1 C RC w R + _ + _ . . + _ . . RC低通滤波器电路作用: 滤掉输入信号的高频成分，通过低频成分。

：带宽：截止角频率幅频特性 0 ω 1 0.707 1 C RC w R + _ . . + _ . . 幅频特性 0 ω 1 0.707 1/RC 0 ω 1/RC 相频特性 RC高通滤波器滤掉输入信号的低频成分，通过高频成分。

网络函数：选频网络 R1 + _ . . + _ . . R2 当R1 R2 R，C1 C2 C，则： 0 ω相频特性幅频特性 0 ω 1/3 当时，输出电压U2达最大值，输出电压与输入电压之比为1/3，且是同相位。

谐振指含有R、L、C的正弦稳态电路，端口所出现的电压与电流同相的现象分类: RLC串联电路的谐振：利用阻抗Z讨论 GCL并联电路的谐振：利用导纳Y讨论 RLC串联谐振 1. 阻抗： j?L R + _ + _ + _ . . + _ 谐振时：特点1 ：谐振时阻抗值最小 RLC 串联谐振 2. 谐振频率：特点2 ：谐振频率仅与L、C有关j?L R + _ + _ + _ . . + _ RLC串联谐振 3. 品质因数Q ：―反映电路选择性能好坏的指标，也仅与电路参数有关 RLC串联谐振 4. 电流：特点3 ：谐振时电流值最大，消耗的平均功率最大推导得： j?L R + _ + _ + _ . . + _ RLC串联谐振 5. 各元件的电压：特点4 ：LC串联部分对外电路而言，可以短路表示 , 大小相等，方向相反, RLC串联谐振当Q 1时, UL0 UC0 QU U, 出现部分电压大于总电压现象串联谐振也称为“电压谐振” j?L R + _ + _ + _ . . + _ . . + _ RLC串联谐振注意：电感L的瞬时功率与电容C的瞬时功率在任何瞬时数值相等而符号相反，它们之间的能量相互补偿。

激励只向电路提供电阻消耗的电能，电路与激励之间没有能量的交换。

. . j?L R + _ + _ + _ . . + _ . . + _ RLC电路的频率特性―幅频特性―相频特性阻抗的频率特性：概念：网络的频率特性是研究正弦交流电路中电压、电流随频率变化的关系（即频域分析）。

阻抗的幅频特性 0 ω R ω0 阻抗的相频特性时，时，时， 0 ωω0 容性感性电流的幅频特性电流的幅频特性显然，当某一具体电路的参数以及电源电压给定后，调节电源角频率即可获得一根I~ω曲线；当另一个具体电路的参数和电源电压给定后，则可获得另一根I~ω曲线。

但这种I~ω曲线用处不大，因为不易从它们的曲线上比较两个电路的电流频率特性. 选择性：电流抑制比 Q1 Q2 Q2 Q1 0 谐振通用曲线显然：Q愈高，曲线愈尖锐，靠近谐振频率附近电流愈大，失谐时电流下降愈快，即对非谐振频率下的电流抑制作用愈大，选择性越好。

谐振电路具有选出所需信号而同时抑制不需要信号的能力称为电路的选择性。

Q1 Q2 Q2 Q1 0 谐振通用曲线结论：Q愈大，带宽愈小，曲线愈尖锐，选择性愈好。

Q愈小，带宽愈大，曲线愈平坦，选择性愈差。

并联谐振 j?L R . . + _ 谐振时：并联谐振 j?L R . . + _ LC并联部分对外电路而言，可以断路表示. 电抗部分对外可断路电抗部分对外可短路 7 6 5 4 3 2 YC+YL 0 XL+XC 0 1 并联谐振串联谐振串联谐振和并联谐振特点对比 LC并联电路 . . + _ R L C 并联谐振时：得到谐振角频率：例：电路如图所示。

若，问哪些端口相当于短路？哪些端口相当于开路？例：已知 , 若u0 t 中不含基波，与ui t中的三次谐波完全相同，试确定C1和C2 . . . . R L C2 ui t +_ C1 u0 t + _ 例：已知求： . . . . L2 R i1 t uC t u t + _ C1 L1 i2 t C2 + _ 南京理工大学电光学院电路 * 作业 4-11 4-13 5-1 例：已知，且与同相，求R、R2、XL及电路消耗的平均功率P。

+ _ -jXC R2 R jXL + _ 平均功率对称时：无功功率对称时：视在功率对称时： 4.8：设UA 220V，负载阻抗，电阻R 22Ω，接于Ul 380V的对称三相电源上。

试求各线电流，及电路消耗的总平均功率P。

. 5.1 非正弦周期交流电路的分析和计算 5.2 RC串联电路的频率特性 5.3 RC串/并联电路的频率特性5.4 RLC串联电路的频率特性与串联谐振 5.5 LC并联电路的频率特性目录电力工程和电子工程中，除了遇到前面已经讨论的直流与正弦信号激励外，还会遇到激励和响应随时间不按正弦规律变化的电路，如电信工程方面传输的各种信号大多就是按非正弦规律变动的。

非正弦周期交流信号的特点: ? 不是正弦波 ?按周期规律变化 ? 信号发生器 ? 电路中有非线性元件 ? 由不同频率的正弦信号共同作用等非正弦周期信号的产生：半波整流电路的输出信号 T t 脉冲信号狄里赫利 Dirichlet 条件： 1. 在一个周期内只含有有限个第一类不连续的点 2. 在一个周期内只含有有限个极值点 3. 在一个周期内函数绝对值的积分为有限值：任何一个满足狄利赫利条件的非正弦周期信号f t ,均可以分解成傅里叶级数。

设一个非正弦周期信号函数都可以分解为：一个恒定分量与一系列不同角频率的正弦量之和 F0 ―恒定分量（直流分量）: 在一周内的平均值展开式可用公式计算或查表 :高次谐波为k次谐波角频率基波，一次谐波: 为基波频率+ _ 含有R、 L、C 的线性电路 us t + _ + _ + _ 含有R、 L、C 的线性电路 us t … + _ U0 u1 t u2 t 1. 根据线性电路的叠加原理，非正弦周期信号作用下的线性电路稳态响应可以视为一个恒定分量和无穷多个正弦分量单独作用下各稳态响应分量之叠加。

因此，非正弦周期信号作用下的线性电路稳态响应分析可以转化成直流电路和正弦电路的稳态分析分析方法：谐波分析法 2. 应用电阻电路计算方法计算出恒定分量作用于线性电路时的稳态响应分量利用直流稳态方法：C ―断路， L ―短路 3. 应用相量法计算出不同频率正弦分量作用于线性电路时的稳态响应分量谐波分析法 4. 对各分量在时间域瞬时值形式进行叠加，即可得到线性电路在非正弦周期信号作用下的稳态响应各次谐波单独作用时，利用相量法：例: 已知求： . . . . R L R C i t iLt iC t u t + _ 例: 已知求： . . . . R L R C i t iL t iC t u t + _ 各分量以瞬时值叠加! 例：已知求： + _ . . . . 1Ω us t 1H 1F is t iL t 非正弦周期量幅值、平均值、有效值周期量有效值的定义：平均值：幅值：峰值非正弦周期量有效值非正弦周期量：将 f t 代入有效值定义式，并利用三角函数的正交性: 则有：非正弦周期电流的有效值: 非正弦周期电压的有效值: 以上两式表明，非正弦周期电流或电压的有效值为其直流分量和各次谐波分量有效值的平方和的平方根注意：使用公式时一定要准确例：求其有效值非正弦周期电流电路的平均功率如图所示一端口N的端口电压u t 和电流i t 的关联参考方向下，一端口电路吸收的瞬时功率和平均功率为： N i t u t + _ . . 非正弦周期电流电路的平均功率一端口电路的端口电压u t 和电流i t 均为非正弦周期量，其傅里叶级数形式分别为 : 在图示关联参考方向下，一端口电路吸收的平均功率 : 非正弦周期电流电路的平均功率将上式进行积分，并利用三角函数的正交性：非正弦周期电流电路的平均功率故：电路的平均功率等于直流分量和各次谐波分量各自产生的平均功率之和，即平均功率守恒上式表明：不同频率的电压与电流只构成瞬时功率，不能构成平均功率，只有同频率的电压与电流才能构成平均功率非正弦周期电流电路的平均功率若某电阻中流过的非正弦周期电流的有效值为I，显然，该电阻吸收的平均功率为：例：已知一端口电路的端口电压u t 和电流i t 均为非正弦周期量，其表达式分别为：求一端口电路吸收的平均功率P ? N i t u t + _ . . 解：例：已知I1 I2 10A, U 200V, R 10Ω, f 50Hz, 电路消耗平均功率2kW，且U与I同相，试求R1、R2、L、C. . . + _ . . R2 R + _ R1 南京理工大学电光学院电路 * *。