电路原理10.3.1非正弦周期电流电路的功率 - 非正弦周期电流电路的功率,非正弦周期电流电路的计算

非正弦条件下功率理论的认识在工程实际中，我们经常遇到电流、电压不按正弦变化的非正弦交流电路。

如：实验室常用的电子示波器中扫描电压是锯齿波；收音机或电视机所收到的信号电压或电流的波形是显著的非正弦形；在自动控制、电子计算机等领域内大量用到的脉冲电路中，电压和电流的波形也都是非正弦的。

1.非正弦周期量的产生和分解1.1非正弦周期量的产生（1）正弦电源(或电动势)经过非线性元件（例如整流元件或带铁心的线圈）时，产生的电流将不再是正弦波；（2）发电机由于内部结构的缘故很难保证电动势是正弦波；（3）电路中有几个不同频率的正弦电源作用，叠加后就不再是正弦波了。

图1. 1 绘出的是三个非正弦周期波形。

(a)方波 （b ）冲波 (c)锯齿波 图1.1非正弦周期波形非正弦信号可分为周期性的和非周期性的两种。

含有周期性非正弦信号的电路，称为非正弦周期性电流电路。

1.2 非正弦周期量的分解将非正弦电压（电流）分解为一系列不同频率的正弦量之和，然后对不同频率的正弦量分别求解，再根据线性电路的叠加原理进行叠加，就可以得到电路中实际的稳态电流和电压。

这就是分析非正弦周期电流电路的基本方法，称为谐波分析法。

实质上就是把非正弦周期电路的计算化为一系列正弦电路的计算 设周期函数f （t ）的周期为T ，角频率ω＝2π/T ，则其分解为傅里叶级数为01m 12m 2km k 0km k k 1()sin()(2)......sin(k )sin(k )f t A A t A t A t A A t ωϕωϕωϕωϕ∞==+++++++=++∑（1.1）式中0A 是不随时间变化的常数，称为()f t 的直流分量或恒定分量；第二项11sin()m A t ωϕ+，其频率与函数()f t 的相同，称为基波或一次谐波；其余各项的频率为基波频率的整数倍，分别为二次、三次、…、k 次谐波，统称为高次谐波。

一般理论分析用数学分析的方法来求解函数的傅里叶级数。

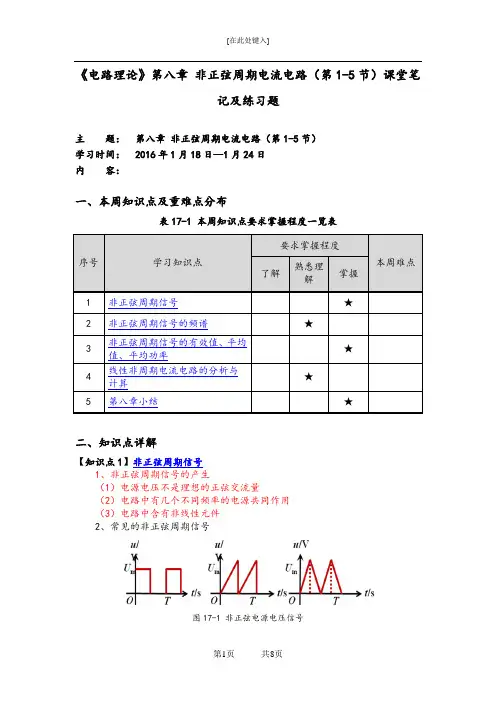
《电路理论》第八章非正弦周期电流电路（第1-5节）课堂笔记及练习题主题：第八章非正弦周期电流电路（第1-5节）学习时间： 2016年1月18日--1月24日内容：一、本周知识点及重难点分布表17-1 本周知识点要求掌握程度一览表序号学习知识点要求掌握程度本周难点了解熟悉理解掌握1 非正弦周期信号★2 非正弦周期信号的频谱★3 非正弦周期信号的有效值、平均值、平均功率★4 线性非周期电流电路的分析与计算★5 第八章小结★二、知识点详解【知识点1】非正弦周期信号1、非正弦周期信号的产生（1）电源电压不是理想的正弦交流量（2）电路中有几个不同频率的电源共同作用（3）电路中含有非线性元件2、常见的非正弦周期信号图17-1 非正弦电源电压信号如果上述激励和响应按一定规律周而复始地变化，称为非正弦周期电压和电流。

3、非正弦周期信号的表示既然两个不同频率的正弦信号叠加后得到一个非正弦周期变化的信号。

所以有：()()k k 0sin k f t A k t ωφ∞==+∑分析非正弦周期电流电路：利用傅里叶级数分解非正弦周期电压或电流；分别计算各频率正弦信号单独作用下的分量；根据叠加定理将分量相加得电路实际电压或电流。

【知识点2】非正弦周期信号的频谱1、周期函数的傅里叶级数周期为T 的时间函数()f t 展开：()()()01s 1s 2s 2s cos sin cos2sin 2f t a a t b t a t b t ωωωω=+++++()0k s k s 1cos sin k a a k t b k t ωω∞==++∑s 2T πω= 傅里叶系数()()()00k s 0k s 01d 2cos d 2sin d T T T a f t t T a f t k t t T b f t k t t T ωω⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩⎰⎰⎰ 01m s 12m s 20km s k 1()sin()sin(2)sin()k f t A A t A t A A k t ωφωφωφ∞==+++++=++∑其中：0k km k k km k km k k kcos sin arctan A aa Ab A A b a φφφ⎧=⎪=⎪⎪=⎨⎪=⎪⎪=⎩谐波分析：将周期函数()f t 分解为直流分量、基波分量和一系列不同频率的各次谐波分量之和。

单元四非正弦周期电流电路一、非正弦周期信号二、非正弦周期量的有效值、平均值及三、非正弦周期电流电路的平均功率四、非正弦周期电流电路的计算一、非正弦周期信号1.非正弦周期信号：随时间周期性地按非正弦规律变化的信号。

2.非正弦周期函数的分解傅里叶级数：若周期为T ，角频率ω=2π/T 的周期函数，满足狄里赫利条件，则的可展开为∑∞=++=++++++++=1022110)sin cos ( sin cos 2sin 2cos sin cos )(k k k k k t k b t k a a t k b t k a t b t a t b t a a t f ωωωωωωωω ∵)t k (sin A sin cos k k ψ+=+ωωωt k b t k a k k ∴+++++=)2sin()sin()(22m 11m 0θωθωt A t A A t f 直流分量基波二次谐波∑∞=++=10)sin(k k k t k A A ψω（K=1、2、3、4…）几种非正弦周期函数的傅里叶级数名称波形傅里叶级数有效值平均值梯形波f (t) =απmA4(sinαsinωt +91sin3αsin3ωt+251sin5αsin5ωt +…+2k1sinkαsinkωt +…)（式中α =Td2π，k为奇数）A mπα-341A m(1－πα)三角波f (t) =2mA8π(sinωt－91sin3ωt+251sin5ωt +…+221kk)1(--sinkωt +…)（k为奇数）3A m2A m名称波形傅里叶级数有效值平均值矩形波f (t) =πmA4(sinωt+31sin3ωt+51sin5ωt +k1sinkωt +…)（k为奇数）A m A m半波整流波f (t) =πmA2(21+4πcosωt+311⨯cos2ωt －531⨯cos4ωt+751⨯cos6ωt －…)2A mπmA全波整流波f (t) =πmA4(21+311⨯cos2ωt－531⨯cos4ωt +751⨯cos6ωt－…)2A mπmA2名称波形傅里叶级数有效值平均值锯齿波f (t) = A m [21－π1(sinωt+21sin2ωt+31sin3ωt +…) ]3A m2A m矩形脉冲波f (t) =A m [ α+π2(sinαπcosωt+21sin2απcos2ωt+31sin3απcos3ωt +…) ]αA mαA m3.几种波形具有对称性的周期函数的傅里叶级数1. 奇函数的傅里叶级数奇函数：f (t )=－f (－t )；奇函数的波形对称于坐标系的原点。

820《电路原理》考试内容范围一、说明主要内容包括电路理论的基本原理和相关电路分析方法两部分，试题的比例为：基本理论部分占比70%，综合分析部分占比30%。

主要参考书：1.《电路》（第5版），邱关源，北京：高等教育出版社，2006.2.《电路（第5版）学习指导与习题分析》，刘崇新,罗先觉，北京：高等教育出版社，2006.二、考试范围1.电路模型和电路定律1.1 掌握电阻、电容、电感、独立电压源、独立电流源、受控电压源、受控电流源诸元件的定义、性质1.2 掌握电流、电压参考方向的概念1.3 熟练掌握基尔霍夫定律2.电阻电路的等效变换2.1掌握电路的等效变换概念2.2熟练掌握等效电阻的计算2.3掌握电源的等效变换3.电阻电路的一般分析方法3.1了解电路的图的概念3.2熟练掌握支路电流法、网孔电流法、回路电流法、结点电压法方程的列写方法及其求解方法4.电路定理4.1熟练掌握叠加定理、替代定理、戴维宁定理、诺顿定理及最大功率传输定理4.2了解特勒根定理、互易定理和对偶原理5.动态电路的时域分析5.1 掌握换路定则并能确定电压、电流的初始值5.2 熟练掌握一阶电路分析的基本方法：零输入响应、零状态响应、全响应5.3 了解二阶电路分析的基本方法6. 正弦稳态电路的分析6.1 掌握正弦量的三要素和有效值6.2 熟练掌握电阻、电感、电容元件电流电压关系的相量形式及电路定律的相量形式6.3 熟练掌握阻抗、导纳、有功功率、无功功率、视在功率和功率因数的概念6.4 熟练掌握正弦电流电路分析的相量方法7.含有耦合电感的电路7.1掌握互感的概念7.2熟练掌握含有耦合电感电路的计算7.3掌握变压器原理、理想变压器的计算8.电路的频率响应8.1理解串联、并联电路的谐振条件8.2掌握其谐振频率的计算方法。

8.3 掌握串联电路频率响应的概念及分析方法8.4了解滤波器的基本概念。

9.三相电路9.1熟练掌握三相电路中电源和负载的联接方式及相电压、相电流、线电压、线电流、三相功率的概念和关系9.2 熟练掌握对称三相电路分析的相量方法9.3 掌握不对称三相电路的概念9.4 掌握三相电路的功率计算方法10.非正弦周期电流电路10.1 了解非正弦周期量的傅里叶级数分解方法10.2 掌握非正弦周期量的有效值、平均值和平均功率的定义和计算方法10.3 掌握非正弦周期电路的计算方法11.线性动态电路的复频域分析11.1掌握拉普拉斯变换的定义及基本性质11.2熟练掌握电阻、电感、电容元件电流电压关系的运算形式及电路定律的运算形式11.3熟练掌握用拉普拉斯变换法分析线性电路12.二端口网络12.1了解二端口网络12.2掌握二端口的方程和参数12.3了解二端口的等效电路、转移函数和二端口的连接。

第九章 非正弦周期电流电路9.1 非正弦周期信号非正弦周期激励−−−−→傅里叶级数一系列不同频率的正弦量及恒定分量之和−−−−−−→线性电路叠加定理各个正弦量及恒定分量单独作用下在电路中产生的同频正弦电流分量和电压分量−−−−→时域叠加电路在非正弦周期激励下的稳态电流和电压。

谐波分析法的实质：把非正弦周期电流电路的计算化为一系列正弦电流电路的计算和直流电流电路的计算。

9.1.1 周期函数分解为傅里叶级数任一周期性函数()()f t f t kT =+，只要满足狄里赫利条件，都可以分解为一个收敛的傅里叶级数。

0111011()[cos()sin()]cos()k k k km k k f t a a k t b k t A A k t ωωωϕ∞=∞==++=++∑∑其中：00,cos ,sin ,arctan kkm k km k k km k k k b A a A a A b A a ϕϕϕ⎛⎫-====-= ⎪⎝⎭. 上式中的每一项，称为正弦谐波分量，简称谐波。

常数0A 称为零次谐波（直流分量），111cos()m A t ωϕ+称为一次谐波，或基波。

上式中的系数，可按下列公式计算：20211()d ()d TT T o a f t t f t t T T -==⎰⎰π1110π21()cos()d ()cos()d()πT k a f t k t t f t k t t T ωωω-==⎰⎰ π1110π21()sin()d ()sin()d()πT k b f t k t t f t k t t T ωωω-==⎰⎰9.1.2 非正弦周期量的频谱傅里叶级数中各次谐波的振幅与初相可以用图形直观地显示，称为频谱图。

幅值频谱：表示振幅的图形。

横轴表示角频率，纵轴表示谐波振幅。

初相频谱：表示初相的图形。

用直线段分别表示各次谐波的初相。

周期性非正弦量的频谱是离散的。

9.2 波形对称性与傅里叶级数的关系根据波形对称性可知傅里叶级数的某些分量为0，可简化计算。