当前位置：文档之家 › 电工基础第八章非正弦周期电流电路习题详解

电工基础第八章非正弦周期电流电路习题详解

  • 格式：doc
  • 大小：275.00 KB
  • 文档页数：6

下载文档原格式

  / 6

合集下载

非正弦周期电流电路和信号的频谱例题

非正弦周期电流电路和信号的频谱例题
非正弦周期电流电路 和信号的频谱例
目录
• 引言 • 非正弦周期电流电路基础 • 信号的频谱分析 • 非正弦周期电流电路的频谱特性
目录
• 信号的频谱与电路响应的关系 • 非正弦周期电流电路和信号的频谱例题解析
01
引言
目的和背景
研究非正弦周期电流电路的行为和特性 分析非正弦周期信号在频域中的表现 为电路设计和信号处理提供理论支持
非线性失真
如果电路中存在非线性元件（如晶体管、放大器等），它们可能会对信号产生非线性失真 ，如谐波失真、交调失真等。这种失真会在信号频谱中产生新的频率成分，从而改变信号 的整体特性。
信号频谱与电路响应的相互作用
信号频谱决定电路响应
信号的频谱特性直接决定了电路对其的响应方式。不同的信号 频谱会导致不同的电路响应，如放大、滤波、谐振等。
02
非正弦周期电流电路基础
非正弦周期信号的定义
非正弦周期信号是指周期性变 化但波形不呈现正弦形状的信
号。
这类信号可以表示为一系列 不同频率正弦波的叠加。
常见的非正弦周期信号有方波、 矩形波、三角波等。
非正弦周期信号的分解
傅里叶级数是非正弦周期信号分解的基础，任何周期信号都可以分解为一 系列正弦波和余弦波的叠加。
频谱分析的原理
01
02
03
傅里叶变换
将时域信号转换为频域信 号的数学工具，通过傅里 叶变换可以得到信号的频 谱。
采样定理
确保从离散采样点恢复原 始信号时不会丢失信息的 理论依据。
窗函数
用于截取信号的一部分进 行分析，以减小频谱泄漏 的影响。
频谱分析的方法
经典傅里叶分析
适用于平稳信号，通过计算信 号的傅里叶变换得到其频谱。

非正弦周期电流电路的分析与计算

非正弦周期电流电路的分析与计算

因此
P I2 R (
0.866 2 ) 100 37.5W 2
8.2 非正弦周期电流电路的有效值和平均功率(5)
（2）us1 和us2频率不同，可用叠加定理计算平均功率。 100 2 i R=100Ω ( ) 2 us1单独作用时： P1 U s1 2 50W R 100 +
uo2 1.6 2 sin(2t 116.6o )V
8.3 非正弦周期电流电路的分析与计算(4)
三次谐波分量sin3t单独作用时，等效电路为： 1Ω + U3 j3Ω
j 0.33 1 j 0.33 j 0.33 1 j 0.33
求得
U 3 0.08 139.4o V
2 us2单独作用时： P U s 2 50 25W 2 R 100 2
+ us2
-
us1
-
所以平均功率为：P=P1+P2=75W
100 2 ) 2 U s1 2 50W P1 R 100 50 2 ( ) 2 U s2 P2 2 12.5W R 100 (
（3）us1 和us2频率不同，可用叠加定理计算平均功率。 us1单独作用时： us2单独作用时：
1Ω
uo(t)
-
求得： uoo=5V
8.3 非正弦周期电流电路的分析与计算(3)
基波分量100sint单独作用时，等效电路为： j1Ω j1 1Ω
+
U1 –
+
求得
U o1
1 j1 j1 1 j1
1 j1
U 1 31.6 63.4o V

-j1Ω 1Ω uo1(t) -
10 2 2 2 ( ) ( ) 7.21 A 2 2

第08章_非正弦周期电流电路

第08章_非正弦周期电流电路
2 T /2 2A bk = ∫ A sin(kωt )dt = [− cos(kωt )] 0 T kωT ⎧2A A ⎪ , k = 1,3,5, = [1 − cos(kπ)] = ⎨ kπ kπ ⎪0, k = 2, 4, 6, ⎩
WangChengyou © Shandong University, Weihai
电路理论基础
第8章 非正弦周期电流电路
16
1 p 1 T T A0 = ∫ f (t )dt ≈ ∑ f ( n ) T 0 p n=1 p 2 p T T 2 T ak = ∫ f (t ) cos( kωt )dt ≈ ∑ f ( n ) cos( kω n ) p n =1 p p T 0 2 p T T 2 T bk = ∫ f (t )sin( kωt )dt ≈ ∑ f ( n )sin( kω n ) T 0 p n =1 p p •将周期分为p个相等的时段，在p个分点上确定出波形曲 线的纵坐标，即f(nT/p), 代入以上各式，求出A0, ak和bk。 •例如：
T
WangChengyou © Shandong University, Weihai
电路理论基础
第8章 非正弦周期电流电路
12
在电路分析中，一般用傅里叶级数的另一种形式：
f (t ) = A0 + ∑ [ Amk cosψ k cos(kω t ) − Amk sinψ k sin( kω t )]
§8.1 非正弦周期电流和电压 §8.2 周期函数分解为傅里叶级数 §8.3 非正弦周期量的有效值、平均功率 §8.4 非正弦周期电流电路的计算
WangChengyou © Shandong University, Weihai
电路理论基础

电路_第八章非正弦周期电流电路和信号的频谱习题及解答

电路_第八章非正弦周期电流电路和信号的频谱习题及解答

第八章 非正弦周期电流电路和信号的频谱本章意图 本章分析线性电路在非正弦周期函数激励下的稳态响应。

首先介绍非正弦周期电流电路的基本概念，然后介绍非正弦周期电流电路的分析计算方法。

主要内容有：周期函数分解为傅里叶级数；非正弦周期电流、电压的频谱；非正弦周期电流、电压的有效值、平均值和平均功率；非正弦周期电流电路的分析计算方法——谐波分析法；电力系统中对称三相电路的高次谐波；傅里叶级数的指数形式及其相应的频谱；傅里叶积分及傅里叶变换。

第一节 内容提要一、周期函数的傅里叶级数形式周期为T 的函数f ( t ) 如果满足狄里赫利条件，则可以展开成级数形式 f ( t ) = a 0+( a 1cos ωt + b 1sin ωt )+ ( a 2cos2ωt + b 2sin2ω t ) + … +( a k cosk ωt + b k sink ωt ) + … = a 0+k=1∞∑( a k cos k ωt + b k sin k ωt )=A 0 +A sin(k t +k k k=1ωψ∞∑)上式中角频率ω=2πT。

以上无穷三角级数称为傅里叶级数。

a 0、a k 、b k 称为傅里叶系数。

比较以上两种级数形式，不难得出 A 0= a 0A k =a b k 2k 2+ψk = arctg ab k k式中，常数项A 0称为 f ( t )的直流分量；A 1sin(ωt+ψ1)称为 f ( t )的一次谐波分量或基波分量；A 2sin(2ωt+ψ2)称为 f ( t )的二次谐波分量；A 3sin(3ωt+ψ3)称为 f ( t )的三次谐波分量⋯。

二次及二次以上的谐波分量称为高次谐波。

习惯上将k 为奇数的分量称为奇次谐波，将k 为偶数的分量称为偶次谐波。

二、非正弦周期电流、电压的有效值、平均值 1、有效值周期电流有效值的定义式为I=10Ti dt 2T ⎰ 对于求非正弦周期电流的有效值上述定义式仍然是实用的。

非正弦周期电流电路分析

非正弦周期电流电路分析
f ( t ) A 0 A 1 s m t i 1 n ) A 2 s ( m 2 t i n 2 ) (
直流分量
2020/7/19
基波
二次谐波
f(t)
A
方
波0
T
f (t) 4A (sint 1 sin3t 1 sin5t
3
5
2T
t
1 sinkt )
k
k 为奇数
f(t)
量和各次谐波分别产生的平均功率之和。
2020/7/19
例：已知某无源二端网络的端电压和电流分别为：
u 5 6 02 0 sit n 3 ( ) 0 42 0 s2 it n 1 ( ) V 0 i 1 0 .52 sit n 2 ( ) 0 0 .32 s2 itn 5 ( ) A 0
（3）把所求得的相量转化为用三角函数表示的瞬时表达式后， 应用叠加定理将属于同一支路的电压或电流分量相加，即得电 路中实际的电压或电流。
注意：应用叠加定理时不能将表示不同频率的电压相量或电流 相量直接相加，更不能将各电压或电流的有效值直接相加。
2020/7/19
5.1 非正弦周期信号的谐波分析
5.1.1 非正弦周期信号的产生
•作用于电路的电源是非正弦的。 •几个不同频率的电源作用于同一电路。 •电路中存在非线性元件。
5.1.2 非正弦周期信号的分解
电工和电子技术中非正弦周期信号一般都满足狄里赫利 条件，可分解成收敛的三角级数，称为傅里叶级数。
如果电压u和电流i同频率的非正弦周期量，并且已知电 压u和电流i的函数表达式，则平均功率为：
PT 10TpdtT 10Tudit
如果电压u和电流i已被分解为傅里叶级数，则由平均功 率的计算公式，可求得平均功率为：

非正弦周期电流电路

非正弦周期电流电路
电路与电子学基础
非正弦周期信号及其谐波分析、有效值
f(t)=(4/π)Am(sinωt+1/3sin3ωt+1/5sin5ωt+…)
有效值 F F12 F32 F52
其中
F1 2
2 Am
F3
2
2 Am
3
F5
22 Am5矩形波的幅度频谱非正弦周期电流电路谐波分析法计算步骤:
（1） 分解：利用傅里叶级数展开法，将已知非正弦周期信号 分 解为一系列频率不同、幅值不同、相位不同的正弦分量 之 和，即将非正弦周期函数分解为傅氏级数。
（2） 单独作用：分别计算在各个频率正弦量（即每一个频率 分 量）单独作用下电路中的响应。
（3） 合成：根据线性电路的叠加原理，将所得到的响应分量 的 时域形式叠加，从而求得实际的稳态响应值。
电路与电子学基础

电子课件-《电工基础(第四版)》-A05-2996 §8-2 周期性非正弦交流电路的计算分析

电子课件-《电工基础(第四版)》-A05-2996 §8-2 周期性非正弦交流电路的计算分析

第八章 非正弦交流电路
电感或电容对不同频率的谐波电流所表现的电抗
不同。在非正弦交流电路中，笼统地讲“阻抗”是没
有意义的，必须具体说明是对哪一次谐波的阻抗。
如基波角频率为ω，电感L对基波的感抗为XL1＝ωL，
对n次谐波的感抗就为 XLn＝nωL ；电容C对基波的容抗
为
X C1
1
C
，而对n次谐波的容抗就为
第八章 非正弦交流电路
试求图示单相半波整流电压的有效值和平均 值各为多少？
单相半波整流电压的波形
解题过程
第八章 非正弦交流电路
三、非正弦交流电的平均功率及计算
周期性非正弦交流电的有功功率等于直流分量
功率与各次谐波功率之和:
或
Байду номын сангаас
P＝P0＋P1＋P2＋P3＋···
P U0I0 U1I1 cos1 U2I2 cos2 U3I3 cos3
课堂小结
1. 周期性非正弦交流电的有效值等于基波及 各次谐波有效值平方和的平方根：
U U02 U12 U22 U32
2. 周期性非正弦交流电的平均功率等于各次 谐波所产生的平均功率之和。
3. 计算周期性非正弦电路通常采用谐波分析 法。
I I02 I12 I22 I32 提示：式中的直流分量可看做是零次谐波。
第八章 非正弦交流电路
二、非正弦交流电的平均值及计算
周期性非正弦交流电在一个周期内的平均值等 于它的直流分量，即：
EP＝E0 UP＝U0
IP＝I0
直流分量为零的周期性非正弦量在一个周期内 的平均值也为零。有时为了能够说明问题，对这样 的周期性非正弦量，计算它在半个周期内的平均值。
让一周期非正弦交流电和一直流电分别通过一等值电阻若在相同时间内两者消耗的电能相等则此直流电的数值就称为该非正弦交流电的有效值

非正弦周期电流电路分析

非正弦周期电流电路分析

u( t ) i ( t ) dt
u( t ) U 0 U nm sin( n 1t n )
n 1
i ( t ) I 0 I nm sin( n 1t n )
n 1

1 (1) T
1 ( 2) T


T 0
T
U 0 I 0 dt U 0 I 0
U n m I n m sin( n 1t n ) sin( n 1t n ) dt
j45
A
i11 (t ) i21 (t ) 1 sin( t 45 ) A

3）三次谐波分量电压单独作用 L1与C1并联后与L2串联的 等效阻抗为
1 j3 C1 1 j 3 L1
j 3 L2 0
该串联支路发生串联谐振，相当于短路
I 13 m U s3m R1 2e A
二端网络吸收的平均功率
P U 0 I 0 U n I n cos n P0 Pn
1、将周期性激励分解为傅里叶级数； 2、根据叠加定理，求每一谐波源单独作用 于电路的响应； 3、将各谐波激励所引起的时域响应叠加， 即得线性电路对非正弦周期性激励的稳态 响应 。
例1. 图a为一个周期性矩形脉冲电流源，用它来激励图b 所示电路
已知：电路的参数为R = 20 , L = 1 mH, C = 1000 pF， T mA。 I p mA T = 6.28 s， ， 2 2 求此电路的端电压u(t)。
具有对称性的周期函数的傅里叶级数展开式的特点： (1) 奇函数(odd function) ： f ( t ) = f ( t )
奇函数的波 形对称于坐 标系的原点
a0 0, 2

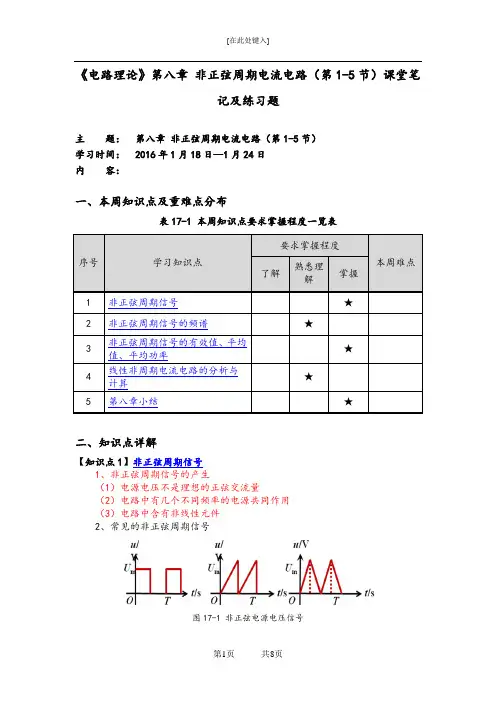
《电路理论》第八章 非正弦周期电流电路(第1-5节)课堂笔记及练习题

《电路理论》第八章 非正弦周期电流电路(第1-5节)课堂笔记及练习题

《电路理论》第八章非正弦周期电流电路（第1-5节）课堂笔记及练习题主题：第八章非正弦周期电流电路（第1-5节）学习时间： 2016年1月18日--1月24日内容：一、本周知识点及重难点分布表17-1 本周知识点要求掌握程度一览表序号学习知识点要求掌握程度本周难点了解熟悉理解掌握1 非正弦周期信号★2 非正弦周期信号的频谱★3 非正弦周期信号的有效值、平均值、平均功率★4 线性非周期电流电路的分析与计算★5 第八章小结★二、知识点详解【知识点1】非正弦周期信号1、非正弦周期信号的产生（1）电源电压不是理想的正弦交流量（2）电路中有几个不同频率的电源共同作用（3）电路中含有非线性元件2、常见的非正弦周期信号图17-1 非正弦电源电压信号如果上述激励和响应按一定规律周而复始地变化，称为非正弦周期电压和电流。

3、非正弦周期信号的表示既然两个不同频率的正弦信号叠加后得到一个非正弦周期变化的信号。

所以有：()()k k 0sin k f t A k t ωφ∞==+∑分析非正弦周期电流电路：利用傅里叶级数分解非正弦周期电压或电流；分别计算各频率正弦信号单独作用下的分量；根据叠加定理将分量相加得电路实际电压或电流。

【知识点2】非正弦周期信号的频谱1、周期函数的傅里叶级数周期为T 的时间函数()f t 展开：()()()01s 1s 2s 2s cos sin cos2sin 2f t a a t b t a t b t ωωωω=+++++()0k s k s 1cos sin k a a k t b k t ωω∞==++∑s 2T πω= 傅里叶系数()()()00k s 0k s 01d 2cos d 2sin d T T T a f t t T a f t k t t T b f t k t t T ωω⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩⎰⎰⎰ 01m s 12m s 20km s k 1()sin()sin(2)sin()k f t A A t A t A A k t ωφωφωφ∞==+++++=++∑其中：0k km k k km k km k k kcos sin arctan A aa Ab A A b a φφφ⎧=⎪=⎪⎪=⎨⎪=⎪⎪=⎩谐波分析：将周期函数()f t 分解为直流分量、基波分量和一系列不同频率的各次谐波分量之和。

第8章非正弦周期交流电路的分析与计算

第8章非正弦周期交流电路的分析与计算
电压有效值为： 解： 电压有效值为： = 100 2 + ( U = U 0 + U1 + U 2 + U 3
2 2 2 2
100 2 50 30 ) + ( ) 2 + ( ) 2 = 129.2V 2 2 2
I = I1 + I 3 = (
2 2
电流有效值为： 电流有效值为：
10 2 2 ) + ( ) 2 = 7.21 A 2 2
1 T
∫
T 0
i 2 dt
平均功率 瞬时功率 平均功率 p=ui
1 P= T
∫
T
0
pdt
进一步推得： 进一步推得： P=P0+P1+P2……+Pk 其中 P0=U0I0 -----------直流分量的功率 直流分量的功率
P1=U1I1cosϕ1 ----------基波分量平均功率， 基波分量平均功率， ϕ 基波分量平均功率
例：图示电路，已知周期信号电压 图示电路， uS(t)=10+100sint+10sin2t+sin3t ，试求 o(t)。 试求u 。 1 + uS 1F 1 – 1H + uo(t) -
单独作用时， 解：直流分量10V单独作用时，等效电路为 直流分量 单独作用时 1 + 10V – 1 + uo0(t) 求得u 求得 o0=5V
π
0
k = 1,2 • • • k = 1,2 • • •
bk =
1
f(t) A 0 -A f(t) A 0 -A
π
∫
2π
0
f ( t ) sin kω td (ω t ),

《电工基础》电子教案 第8章 周期性非正弦交流电路

《电工基础》电子教案 第8章 周期性非正弦交流电路
• 8. 2. 3平均功率
• 周期性非正弦电流电路的平均功率定义为瞬时功率在一个周期内的平 均值。通常所说的功率就是指平均功率。
下一 返回
8. 2周期性非正弦电流电路中的有效值、 平均值、平均功率
• 根据三角函数的正交性，对于不同次谐波电压、电流的乘积，它们的 平均值均为零。
• 周期性非正弦电流电路的平均功率等于恒定分量构成的功率和各次谐 波平均功率的代数和。由上式可知，只有同频率的电压和电流相互作 用才产生平均功率，不同频率的电压和电流只能产生瞬时功率，不能 产生平均功率。
• 奇函数的傅里叶级数中只含有正弦项，不含直流分量和余弦项。
• 3.周期函数为偶函数
• 若周期函数满足f(t)=f(-t)，则为偶函数，其波形对称于纵轴，如表8.1 中半波整流波、全波整流波均为偶函数。
• 4.周期函数为镜像对称的函数(奇谐波函数)
• 若周期函数满足
即将波形移动半个周期后便与原波
形对称于横轴，称为镜像对称函数，如图8. 3所示，图中虚线所示为
上一页 返回
8. 3 周期性非正弦电流电路的计算
• 本章仅讨论线性周期性非正弦电流电路的分析和计算方法，主要是利 用数学中的傅里叶级数，将周期性非正弦信号分解为直流分量和一系 列不同频率的正弦量之和;然后分别计算直流分量和各种频率正弦量 单独作用时电路的响应;最后再根据线性电路的叠加定理，把所得分 量的瞬时值相加，就可以得到电路中实际的电压和电流。这种分析电 路的方法称为谐波分析法。它实质上就是把周期性非正弦电流电路的 计算化为一系列正弦电流电路的计算。其分析电路的具体步骤如下:
周期性非正弦量。因此，非正弦电动势在线性电路中所产生的电流波 形，也将是非正弦的。 • 当线性电路中几个频率不同的正弦激励共同作用时，由于它们的频率 不同，电路中的总电动势将不再是正弦波，因此电路中的电压、电流 响应也不是正弦量。 • 2.电路中存在非线性元件 • 当电路中存在非线性的电阻、电感或电容元件时，即使是正弦激励， 电路中也会产生非正弦响应。 • 将一个铁芯线圈(非线性电感)接到正弦电源上，其电压为正弦波形。

电工基础第八章《非正弦周期电流电路》习题

电工基础第八章《非正弦周期电流电路》习题

第八章非正弦周期电流电路一、感抗ωL=5Ω中通过电流i(t)=[5sin(ωt+60°)+10sin(3ωt+30°)]A时，则其端电压UL(t)=?二、容抗1/ωC=12Ω的电容器端电压u(t)=[24sin(ωt+20°)+12sin(3ωt+7 0°)]V时，流过该电容的电流ic(t)=?三、当ωL=4Ω的电感与1/ωC=36Ω的电容并联后，外加电压u（t）=（18sin ωt+3cos3ωt）V，总电流的有效值为大小？四、有效值为100V的正弦电压加在电阻可以忽略的线圈两端，测得线圈中电流有效值为10A，当电压中含有三次谐波分量，而有效值仍为100V时，电流的有效值为8A，试求此电压的基波和三次谐波的有效值。

五、R、L、C串联电路外加电压u(t)=[100sin314t+50sin(942t-30°)]V,电路中电流为i（t）=[10sin314t+1.755sin（942t+θ2）]A。

求：（1）R、L、C的值；（2）θ2的值；（3）电路消耗的平均功率。

六、R、L、C串联电路外加电压u(t)=[10+80sin(ωt+60°)+18sin3ωt]V ,R=6Ω, ωL=2Ω, 1/ωC=18Ω。

求：（1）电路中的电流i（t）及其有效值I；（2）电源输出的平均功率。

七、在R、C串联电路中，已知电流为i（t）=(2sin314t+sin942t)A，电源电压有效值为155V，且不含直流分量，电源输出的功率为150W，求：电阻R和电容C的值。

八、电阻可以忽略的一个线圈，接到有效值为100V的正弦电压时，电流的有效值为10A。

接到含有基波和三次谐波，有效值也为100V的非正弦电压时，电流的有效值为8A。

试求非正弦电压的基波和三次谐波的有效值。

九、R=10Ω、C=159μF的电阻电容串联电路接到us(t)=(50+190sin100πt)V的电压源。

《电工基础》课后习题解答

《电工基础》课后习题解答

解 （1）电路发生断路故障，故障点在灯泡处。 （2）电路发生短路故障，短路点在灯泡处。 （3）电路发生断路故障，故障点在电流表处或 在电池和滑线电阻处。 （4）电路中电阻过大，灯泡电压很低，接触点 处接触不良，滑线电阻阻值过大。
图1－39
1－15 在图1－40所示电路中，若以f点作为参考点，试计 算c、d两点的电位。
图1－44
1－21 在图1－45所示电路中，已知U1=1V，试求电阻R。
解 各电量参考方向如图所示
1 I1 1 A 1 U 2 12 1 11 V 11 5 .5 A 2 I 3 I 2 I 1 5 .5 1 4 .5 A I2 U 4 18 1 3 4.5 5.5V 5 .5 5 .5 A 1 I I 4 I 3 5 .5 4 . 5 1 A I4 U 12 5.5 6.5V 6 .5 R 6.5 1
解
12 I 1 2A 24 6 图1－40 I2 2A 1 2 V c U cf U af U ba U cb 12 2 2 0 8V V d U df U dc U cb U ba U af 2 1 0 2 2 12 10V
1－3 下述说法中错误的是（ D ）。 A.电阻元件是一种耗能元件，当其中有电流流过时，它总是吸收功率， 消耗电能。 B.电容元件是一种储能元件，它所储存的电场能量与其极板上的电荷量 平方成正比。 C.电感元件是一种储能元件，它所储存的磁场能量与其磁链平方成正比。 D.电压源和电流源是有源元件，当它们与外电路接通时，它们总是发出 电能。
1－19 求图1－43所示电路中的电压Uab。
图1－43
解 设电流I1参考方向如图所示

周期性非正弦电流电路的计算

周期性非正弦电流电路的计算

(1)当直流分量为 U0 10V 单独作用时，等效电路如图7.5(b)所示, 此时电感相当于短路, 而电容相当于开路。各支路电流分别为
I1(0)
U0 R1
10 5
2A
I2(0) 0
I(0) I1(0) 2A
(2)当基波分量u1(t) 141.4sint V 单独作用时，等效
电路如图7.5(c)所示，用相量法计算如下：
L
LCC源自输入C输出
输入
L
输出
（a）低通
（b）高通
图7.6 简单滤波器
电工基础
周期性非正弦电流电路的计算
u(t)
i R1 i1 R2 i2
L
C
I 0
I10R2 I20
Uo
R1
(a)
(b)
u1 (t )
i1 R1 i1(1) R2
i2(1)
L
C
i3 R1 i1(3)R2 i2(3)
u3(t )
L
C
(c)
图7.5 例7.4图
(d)
•
U1 100 0 V
•
•
I 1(1)
U1
100 0 18.6 21.8 A
R1 jL 5 j2
•
•
I 2(1)
U1
100 0 5.55 56.3 A
R2 jL 10 j15
•
•
•
I (1) I1(1) I 2(1) (18.6 21.8 5.55 56.3) 20.5
6.38 A
周期性非正弦电流电路的计算
(3)当三次谐波分量 u3 (t) 70.7 sin(3t 30 ) V 单独作用时，
等效电路如图7.5(d)所示。注意，此时，感抗

电工基础第八章 非正弦周期电流电路

电工基础第八章 非正弦周期电流电路
3.视在功率
非正弦电流电路的视在功率定义为电压和电流有效值的乘积，即
S UI U02 U12 ... Uk2 ... I02 I12 ... Ik2 ...
注意:视在功率不等于各次谐波视在功率之和。
第四节 非正弦周期电流电路的分析
非正弦周期电路稳态电路的分析计算采用谐波分析法。 其理论依据是线性电路的叠加定理。
交流量的平均值，也称绝对平均值或整流平均值。即
Irect

1 T
T
i dt
0Leabharlann 1T Urect T
u dt
0
第三节 非正弦周期电流电路中的有效值、平均值、平均功率
三、非正弦电流电路的功率
1.平均功率（有功功率） 根据平均功率的定义式:
P 1
T
p(t)dt
T0
可得非正弦电流电路的平均功率为
f (t) a0 (a1 cost b1 sin t) (a2 cos 2t b2 sin 2t) ...
(ak cos kt bk sin kt)

a0 (ak cos kt bk sin kt) k 1
a0
,
a k
,
bk
为傅里叶系数，可按下面各式求得
第四节 非正弦周期电流电路的分析
例８－3 已知图中u（t）=［１0+100 2 sint+50 2 sin（3t+30）］V，
L=2，1/C=15，
R1=5， R2=10 。
求:各支路电流及它们
的有效值；
电路的有功功率。
图8-4 例8-3图
第四节 非正弦周期电流电路的分析
解：因为电源电压已分解为傅里叶级数，可直接计算各次谐波作用下的

第8部分非正弦周期电流电路共13页文档

第8部分非正弦周期电流电路共13页文档

0.4H
j4
2
US1
102 FLeabharlann uS2 iSu
2 10V

2A
U0
j10 2 200 V
20 A
U1
(a)
直流分量（b作）用电路
基波分（量c作） 用电路
解：直流分量响应 U 0 1V 0 2 2 A 1V 4
交流分量响应 [(21j4)j1 1 0]U 12j1V 0 02A解 得U 120 90V
u Um
解： u(t) Um t （0<t<T)
T
U T 10 T u 2 (t)d tT 10 T (U T m t)2 d tU T m 3 2
O
T
2T t U T 10 T u 2 (t)d tT 10 T (U T m t)2 d tU T m 3 2(t3 3 )|T 0 U 3 m
本章内容：线性、非正弦、周期电流电路的计算
8．1 周期函数的傅立叶级数分解
满足一定条件的周期函数可以分解为傅立叶级数：

1、 f(t)A0 [akcok st)(bksiknt()] k1
其中：


2 T
( T为信号f(t)的周期）
A0T 1
0Tf(t)dt21
I1mU Z 1 1 m8 6 0 0 8 0.6 80.7 58.6 8A
3次谐波：
Z 3R j(3 L 3 1 C ) 2j0 2 0 阻性
I3mU Z33m22 000 1 00A
8．3 非正弦周期电流电路的计算
2
f(t)dt
0
ak
2 T
T

非正弦周期电流电路

非正弦周期电流电路

非正弦交流电路
非正弦周期电流电路基本的分析方法称为谐波分析法，它是正弦电流电路分析方法的推广。

计算步骤为：首先利用数学中的傅立叶级数，将非正弦周期激励分解成为一系列不同频率的正弦量之和；再根据线性电路的叠加原理，分别计算出各个频率分量单独作用于电路时在电路中产生的响应分量；最后把各响应分量按时域形式进行叠加，就得到了电路在非正弦周期激励下的响应。

若一端口网络端口上的电压、电流表达式为：
1、非正弦计算（一）
分析：由于已给定电压源的付里叶级数展开式，只要按步骤计算出在每一电压分量作用于电路产生的电流响应，再按瞬时值叠加即可。

需要注意的是：直流分量作用电路时，电容相当于开路，正弦分量作用于电路时，随着频率的增高，容抗减小。

方程式及结果如下：
最后将电流叠加并代入功率计算公式：
2、非正弦计算（二）
方程式及结果如下：
3、非正弦计算（三）
分析：若负载中不含基波分量，则电源中基波分量必然降在传输线上，则L、C发生并联谐振；而4ω的谐波分量全部传至负载，要求传输线4ω的谐波阻抗为0；故必须L1、C与L2发生串联谐振，代入串联谐振条件，则电路可解。

方程式及结果如下：。

第8章非正弦周期电流电路

第8章非正弦周期电流电路
第8章 非正弦周期电流电路
第八章 非正弦周期电流电路
一、特点：按周期规律变化，但不是正弦量。
工程实际中，非正弦周期波形较为常见，如：脉冲波形、三 角波、方波、锯齿波、半波整流波形等等；
u
u
t
方波电压 u
t
锯齿波 u
t 脉冲波形
t 半波整流波形
第8章 非正弦周期电流电路
二、非正弦周期信号的产生： (1).电源提供的电压或电流是非正弦周期变化的； (2).电路中有不同频率的电源共同作用； (3). 若电路中存在非线性元件。
3.正弦、余弦的平方在一个周期内的平均值为1/2 。
1
2
2sin2ktd(t)1
0
2
1
2
2cos2ktd(t)1
0
2
第8章 非正弦周期电流电路
一、非正弦周期量的有效值
设非正弦周期电流为： iI0 Ikmsin(ktk)
k1
根据有效值定义：
I 1 T i2dt T0
I T 10T[I0k 1Ikmsin(ktk)]2dt
T/2 T
t
A0
Hale Waihona Puke 1 TTf (t)dt
0
0
π 2π -Um
BkmT2
T
f(t)sinkωtdt
0
1 2f(t)sin(kt)d(t) 0
1 0 U m s in (k t)d ( t) 2 U m s in (k t)d ( t)
2Um
sin(kt)d(t)
0
2Um
1k cos(kt)0
例如：
(1).用磁电系仪表（直流仪表）测量，所得结果将是非正弦量 的恒定分量(即平均值)；
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第八章 非正弦周期电流电路习题解答
8-1解：直流分量单独作用时，将电容开路，电源u(t)短路，其余保留。

交流分量单独作用时，将电源Ｕ短路，其余保留。

8-2解：电流表达式为24sin i t A ω=+
在直流分量(0)2I A =作用下，电感看作短路，电源电压(0)22040U V =⨯=； 在基波分量(1)()4sin I t t A ω=
作用下，(1)0(2030)10256.3U j V =+=∠
电源电压表达式为()4056.3)u t t V ω=++
平均功率402102cos56.3240P W =⨯=
无功功率102sin 56.3240Q Var ==
视在功率2242379.5.2S V A =+= 8-3解：（1）在电压的直流分量(0)10U V =单独作用下，电容看作开路，电路中无电流，
即 (0)0I A =
在一次谐波下，(1)()80sin(60)u t t V ω=+单独作用下：
(1)(1)(1)8060 4.7129.46218
U I A Z j j ∠===∠+- 在三次谐波(3)()18sin3u t t V ω=单独作用下：
(3)(3)(3)180
30666
U I A Z j j ∠===∠+- 电路中的电流为() 4.7sin(129.4)3sin3t i t t A ωω=+
+
其有效值为 3.94I A == （2）电源输出的功率为：
1180 4.7cos(60129.4)183cos 09322
P W =⨯⨯-+⨯⨯=
8-4解：（1）一次谐波电压、电流是(1)(1)()100sin314()10sin314u t t V i t t A ==；，它们
同相位，即：(1)(1)L C X X =
100010
100
R ∠==Ω∠ 有： 1
314(1)314L C = 三次谐波时，22215010(942)()(2)942 1.755L C +-= 联立求解（1）、（2）两式，可得31.9318.4L mH C F μ==，
（2）(3)1109421030 3.3328.569.5942Z j L j j j C
=+-=+-=∠Ω 即 3069.599.5θθ--==-，
（3）电路消耗的功率
1110010cos 050 1.755cos 69.5515.422
P W =⨯⨯+⨯⨯= 8-5解：电流()S i t 的直流分量(0)2S I A =单独作用时，电容开路，即L 、C 串联支路为开路。

(0)(0)2R S I I A ==
一次谐波(1)()10sin S i t t A ω=单独作用时
531010
100L ω-=⨯=Ω 5611100100.110
C ω-==Ω⨯⨯ L 、C 串联支路谐振相当于短路 (1)0R I A =
二次谐波(2)()3sin 2S i t t A ω=单独作用时
2200L ω=Ω
1502C
ω=Ω L 、C 串联支路的复阻抗为150j Ω (2)15030 1.853.1200150
R j I A j =∠⨯=∠+ 即 ()2 1.8sin(253.1)R t i t A ω=++
其有效值为 2.37R I A ==
8-6解：（1）电路在直流分量作用下，电感相当于短路，电容相当于开路
(0)(0)(0)50500.5100R L U U V I A ===
=， 一次谐波作用下：3336110210250102010
L C X X --=⨯⨯=Ω==Ω⨯⨯， (1)(1)(1)(1)(1)(1)(1)(1)(1)(1)1000.101001000.29050
0.10.20.2263.40.2263.42100
9.6 2.34()509.6sin( 2.34)R R R C C L R C L R L U I A R U I A jX j I I I j A
U I jX U j V
u t t V ω∠=
==∠∠===∠--=+=+=∠=+=∠⋅+∠=∠=+
+
其有效值50.5U V = （2）电路总电流即 ()0.50.22sin(63.4)L i t t A ω=++
电源输出功率为
1500.59.60.22cos(2.3463.4)25.512
P W =⨯+⨯⨯-= 8-7解：在电压直流分量(0)30U V =单独作用下，电容看作开路，电感看作短路，电阻电流
等于电感电流，即1(0)2(0)30215
I I A ===，电容电流(0)0C I A =，电容电压(0)0C U V =。

在电压一次谐
波(1)()u t tV ω=单独作用下，电路复阻抗为：
(1)10(90)151511.251090
j j Z j j j -=+=+Ω- 电阻电流：1(1)1500.836.91511.25
I A j ∠==∠-
+ 电感电流：2(1)900.836.90.936.91090j I A j j -=∠-⨯
=∠-- 电容电压：(1)(1)0.936.910953.1C L U U j V =∠-⋅=∠
在电压三次谐波3()u t t V ω=单独作用下，13303L C
ωω=
=Ω，L 、C 并联谐振，相当于开路
1(3)0I A =，2(3)10900.33030
I A j ∠==∠，(3)(3)1090C U U V ==∠ 所以
1()236.9)i t t A ω=+-
2()236.9)t i t t A ωω=+-+ (
)53.1)102sin(390)C u t t
t V ωω=
++
+ 它们的有效值分别为：
12 2.15 2.2213.45C I A
I A U V
======
即三表读数分别为2.15A ；2.22A ；13.45V 。

8-8解：在电源电压直流分量(0)20U V =作用下，电容相当于开路，电感相当于短路，互感
不起作用。

1(0)2(0)201020I A I A =
== 在电压一次谐波(1)()20sin u t t V ω=单独作用下，可列方程：
1(1)2(1)1(1)
111(1)2(1)2()1()0I R j L I j M U I j M I R j C ωωωω⎧++=⎪
⎨+-=⎪⎩
代入数据：
1(1)2(1)1(1)2(1)(24)0(364)0
I j I j I j I j
j ⎧++⋅=⎪⎨⎪⋅+-+=⎩ 解之得：1(1)361.7I =∠
-；2(1)0.84
118I A =∠-
1()2()1063.4)118)t t i t A
i t
A
ωω=+-=-
它们的有效值为： 1210.40.84I A
I A
=== 即两表读数分别为10.4;0.84A A
8-9解：因为电路功率2
P I R =，
2150 2.5R R == 60R =Ω
设电源电压12()))u t U t U t ωϕωϕ=+++，由已知条件有：
(1)(2)155
U U ===
联立求解可得85.495C X =Ω，37.2C F μ=。

8-10解：要将基波电流全部滤掉，则1L 、C 并联电路发生并联谐振
11266
11111010L L H C C ωωω-=
===⨯， 31110L C ωω==Ω 要将4W 的谐波电流送至负载，电路应对该谐波发生谐振
2114(4//)04j L j L j
C
ωωω+-= 即 33323310410()44100104104j j j L j j ⨯-⨯+=⨯-， 得
3322441010015
66.7j L j
L mH ⨯-⨯== 8-１1解：要求在2()u t 中不含基波分量，则电感与1C 支路应对基波发生串联谐振，即：
4341
111010C 10-⨯⨯= 得 110C F μ=，1
110C ω=Ω 要求在2()U t 中全部取出三次谐波分量，则电路对三次谐波发生并联谐振，即：
4242101(310)()33101013103310j j j C j j j C ⨯--⨯=∞⨯--⨯ 4210131003310C ⨯--=⨯ 得 2 1.25C F μ=。