最小二乘法线性详细说明共47页

第五章线性函数的最小二乘处理最小二乘原理应用时的条件是：函数关系确定已知、等精度、误差独立、无偏估计得到满足，在众多的N个测量方程中利用最小二乘原理求得t个（t＜／N）参数的最佳估计值。

如前所叙，在随机因素作用下，测量次数较多时，计算的结果就会更精密，测量次数往往大于待求未知量的个数，因而出现N＞t的现象就成为自然而然的事情了。

众所周知，当N＝t时可由线性代数知识求得一组唯一正确解。

当N＞t时，代数解法则无能为力了。

也许读者会提出另外一个问题：既然N＞t，可由N中取出t个方程来求解，而把（N-t）个方程弃掉，问题不就解决了吗？答案是不行的。

这样求解后的结果不是最佳值，有时会与最佳值离歧很大。

最小二乘法是一种数学原理，高斯于1809年在他的名著《天体沿圆锥截面绕太阳运动的理论》一书中，发表了他发现的最小二乘原理并应用于测量之后，在许多科学领域及技术领域中得到越来越多地应用。

5.1 函数为直接测量值得线性组合5.1.1 测量方程式函数中可能存在着多个待定参数，根据该函数关系可列出多个测量后的方程式，该方程式称作测量方程式。

设含有t个待求参数Xj(j=1,2,…,t)的函数关系已知，表现为线性组合，即Xj是待定系数的真值，aj是在某具体测量条件下获得的直接测量值，经N次测量（N>t）后，理应得到N个函数真关系式。

为了表达更简洁，可将各方程中系数用aij(i=1,2, …,N;j=1,2, …,t)表示，上述方程可简写成量值Y经N次测量后的测量值用Mi表示，则上述方程变为测量方程式，又称测量条件方程，式中，aij及Mi是在某具体测量条件下的直接测量值，Mi含有误差，即Mi≠Yi。

5.1.2 剩余误差方程式若用同直接测量时一样，可将称作剩余误差。

由此便可得到N个剩余误差方程式可以看出，剩余误差是各最可信赖值的函数，即5.1.3 正规方程组现在以三个待求量x1,x2,x3为例，说明建立正规方程组的过程，该计算方法和过程及结论，可推广到t个待求量中去。

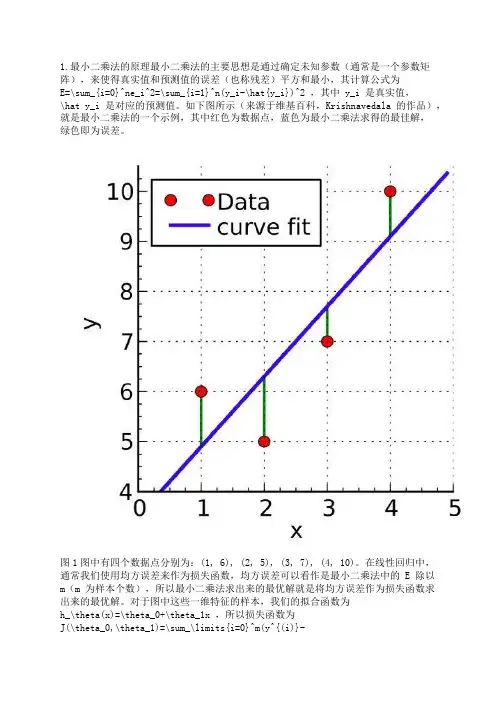
1.最小二乘法的原理最小二乘法的主要思想是通过确定未知参数（通常是一个参数矩阵），来使得真实值和预测值的误差（也称残差）平方和最小，其计算公式为E=\sum_{i=0}^ne_i^2=\sum_{i=1}^n(y_i-\hat{y_i})^2 ，其中 y_i 是真实值，\hat y_i 是对应的预测值。

如下图所示（来源于维基百科，Krishnavedala 的作品），就是最小二乘法的一个示例，其中红色为数据点，蓝色为最小二乘法求得的最佳解，绿色即为误差。

图1图中有四个数据点分别为：(1, 6), (2, 5), (3, 7), (4, 10)。

在线性回归中，通常我们使用均方误差来作为损失函数，均方误差可以看作是最小二乘法中的 E 除以m（m 为样本个数），所以最小二乘法求出来的最优解就是将均方误差作为损失函数求出来的最优解。

对于图中这些一维特征的样本，我们的拟合函数为h_\theta(x)=\theta_0+\theta_1x ，所以损失函数为J(\theta_0,\theta_1)=\sum_\limits{i=0}^m(y^{(i)}-h_\theta(x^{(i)}))^2=\sum_\limits{i=0}^m(y^{(i)}-\theta_0-\theta_1x^{(i)})^2 （这里损失函数使用最小二乘法，并非均方误差），其中上标(i)表示第 i 个样本。

2.最小二乘法求解要使损失函数最小，可以将损失函数当作多元函数来处理，采用多元函数求偏导的方法来计算函数的极小值。

例如对于一维特征的最小二乘法， J(\theta_0,\theta_1) 分别对 \theta_0 ， \theta_1 求偏导，令偏导等于 0 ，得：\frac{\partial J(\theta_0,\theta_1)}{\partial\theta_0}=-2\sum_\limits{i=1}^{m}(y^{(i)}-\theta_0-\theta_1x^{(i)}) =0\tag{2.1}\frac{\partial J(\theta_0,\theta_1)}{\partial\theta_1}=-2\sum_\limits{i=1}^{m}(y^{(i)}-\theta_0-\theta_1x^{(i)})x^{(i)} = 0\tag{2.2}联立两式，求解可得：\theta_0=\frac{\sum_\limits{i=1}^m(x^{(i)})^2\sum_\limits{i=1}^my^{(i)}-\sum_\limits{i=1}^mx^{(i)}\sum_\limits{i=1}^mx^{(i)}y^{(i)}}{m\sum_\limits{i=1}^m(x^{(i)})^2-(\sum_\limits{i=1}^mx^{(i)})^2} \tag{2.3}\theta_1=\frac{m\sum_\limits{i=1}^mx^{(i)}y^{(i)}-\sum_\limits{i=1}^mx^{(i)}\sum_\limits{i=1}^my^{(i)}}{m\sum_\limits{i=1}^m(x^{(i)})^2-(\sum_\limits{i=1}^mx^{(i)})^2} \tag{2.4}对于图 1 中的例子，代入公式进行计算，得： \theta_0 = 3.5, \theta_1=1.4,J(\theta) = 4.2 。

最小二乘法基本原理：成对等精度测得一组数据，试找出一条最佳的拟合曲线，使得这条曲线上的各点值与测量值的平方和在所有的曲线中最小。

我们用最小二乘法拟合三次多项式。

最小二乘法又称曲线拟合，所谓的“拟合”就是不要求曲线完全通过所有的数据点，只要求所得的曲线反映数据的基本趋势。

曲线的拟合几何解释：求一条曲线，使所有的数据均在离曲线的上下不远处。

第一节 最小二乘法的基本原理和多项式拟合 一最小二乘法的基本原理从整体上考虑近似函数)(x p 同所给数据点),(i i y x (i=0,1,…,m)误差i i i y x p r -=)((i=0,1,…,m)常用的方法有以下三种：一是误差i i i y x p r -=)((i=0,1,…,m)绝对值的最大值im i r ≤≤0max ，即误差 向量T m r r r r ),,(10 =的∞—范数；二是误差绝对值的和∑=mi ir 0，即误差向量r 的1—范数；三是误差平方和∑=mi ir02的算术平方根，即误差向量r 的2—范数；前两种方法简单、自然，但不便于微分运算 ，后一种方法相当于考虑 2—范数的平方，因此在曲线拟合中常采用误差平方和∑=mi ir02来 度量误差i r (i=0，1，…，m)的整体大小。

数据拟合的具体作法是：对给定数据 ),(i i y x (i=0,1,…，m)，在取定的函数类Φ中,求Φ∈)(x p ,使误差i i i y x p r -=)((i=0,1,…,m)的平方和最小，即∑=m i ir 02=[]∑==-mi ii y x p 02min)(从几何意义上讲，就是寻求与给定点),(i i y x (i=0,1,…,m)的距离平方和为最小的曲线)(x p y =（图6-1）。

函数)(x p 称为拟合 函数或最小二乘解，求拟合函数)(x p 的方法称为曲线拟合的最小二乘法。

Φ可有不同的选取方法.6—1二多项式拟合假设给定数据点),(i i y x (i=0,1,…,m)，Φ为所有次数不超过)(m n n ≤的多项式构成的函数类，现求一Φ∈=∑=nk k k n x a x p 0)(,使得[]min )(00202=⎪⎭⎫⎝⎛-=-=∑∑∑===mi mi n k i k i k i i n y x a y x p I (1)当拟合函数为多项式时，称为多项式拟合，满足式（1）的)(x p n 称为最小二乘拟合多项式。