最小二乘法线性详细说明

最小二乘法求系数模型最小二乘法是一种常用的数据拟合方法，用于求解线性回归问题中的系数模型。

该方法以最小化残差平方和为目标，通过对数据进行拟合来确定模型的系数。

本文将详细介绍最小二乘法的原理和应用。

一、最小二乘法原理最小二乘法的核心思想是找到一个最佳的拟合曲线或平面，使得该曲线或平面与实际数据之间的残差平方和最小。

在线性回归问题中，我们假设因变量y与自变量x之间存在线性关系，即y = β0 + β1x + ε，其中β0和β1为待求的系数，ε为误差项。

我们的目标是找到最佳的β0和β1，使得残差平方和最小。

具体而言，最小二乘法的步骤如下：1. 假设因变量y与自变量x之间存在线性关系，即y = β0 + β1x + ε。

2. 根据给定的数据集，计算每个数据点的残差，即实际值与拟合值之间的差异。

3. 计算残差的平方和，即求解目标函数：S(β0, β1) = Σ(yi - (β0 + β1xi))^2。

4. 对目标函数进行求导，并令偏导数等于零，求解β0和β1的值。

5. 对得到的β0和β1进行验证，并判断模型的拟合程度。

二、最小二乘法的应用最小二乘法可以应用于各种领域的数据拟合问题，例如经济学、统计学、金融学等。

下面以经济学中的消费函数为例，说明最小二乘法的应用。

在经济学中，消费函数描述了消费支出与收入之间的关系。

我们可以假设消费函数为线性函数，即 C = β0 + β1Y + ε，其中C为消费支出，Y为收入，β0和β1为待求的系数，ε为误差项。

我们的目标是通过最小二乘法来估计β0和β1的值。

具体步骤如下：1. 收集相关数据，包括消费支出和收入的观测值。

2. 根据最小二乘法的原理，计算每个数据点的残差，即实际的消费支出与拟合值之间的差异。

3. 计算残差的平方和，即目标函数：S(β0, β1) = Σ(Ci - (β0 + β1Yi))^2。

4. 对目标函数进行求导，并令偏导数等于零，求解β0和β1的值。

5. 对得到的β0和β1进行验证，并根据模型的拟合程度来评估消费函数的有效性。

—26 n 基本概念与数据处理4.最小二乘法线性拟合(非常好)我们知道，用作图法求出直线的斜率a 和截据b ，可以确定这条直线所对应的经验公式，但用作图法拟合直线时，由于作图连线有较大的随意性，尤其在测量数据比较分 散时，对同一组测量数据，不同的人去处理，所得结果有差异，因此是一种粗略的数据 处理方法，求出的a 和b 误差较大。

用最小二乘法拟合直线处理数据时 ，任何人去处理同一组数据，只要处理过程没有错误，得到的斜率a 和截据b 是唯一的。

最小二乘法就是将一组符合 Y=a+bX 关系的测量数据，用计算的方法求出最佳的a和b 。

显然，关键是如何求出最佳的a 和b 。

(1)求回归直线设直线方程的表达式为： y 二 a bx(2-6-1)要根据测量数据求出最佳的 a 和b o 对满足线性关系的一组等精度测量数据 (X i ，y i )， 假定自变量X i 的误差可以忽略，则在同一 X i 下，测量点y i 和直线上的点 a+bx i 的偏差d i 如下：d i = y i - a - bx-id^ — y 2~ a - bx 2d n = yn ~a ~ bx n显然最好测量点都在直线上(即 d i =d 2=,, =d n =0),求出的a 和b 是最理想的，但测量点不可能都在直线上， 这样只有考虑d i 、d 2、”、 d n 为最小，也就是考虑d i +d 2+,, +d n 为最小，但因d i 、d 2、，，、d n 有正有负，加起来可能相互抵消，因此不可取；而|d i | + |d 2|+ ,,+ |d n |又不好解方程，因而不可行。

现在米取一种等效方法：当d^+d/ + ,,+d n 2222对a 和b 为最小时，d i 、d 2、，，、 d n 也为最小。

取(d i +d 2 +,, +d n )为最小值，求 a和b 的方法叫最小二乘法。

nD 八 d i 2i JD 对a 和b 分别求一阶偏导数为:n-na -b ' X i ]i T nnD 八 d i 2 = i ±(2-6-2)-=D-=b:D-a n 一2「y ii 3 n一2[、X i y i i 』n基本概念与数据处理—27 - -b' X j2]i d—28 - n 基本概念与数据处理2 ' x -x将a 、b 值带入线性方程y = a bx ，即得到回归直线方程。

最小二乘法公式计算公式最小二乘法是一种常用的数据拟合方法，它通过最小化观测数据与拟合曲线之间的残差平方和，来确定拟合曲线的参数。

在数学领域中，最小二乘法通过求解线性方程组来确定问题的最优解。

本文将详细介绍最小二乘法的计算公式，并给出应用示例。

1. 最小二乘法的一般形式假设我们有一组观测数据，包括自变量x和因变量y。

我们希望找到一个拟合曲线，使得观测数据与该曲线的残差平方和最小。

拟合曲线的一般形式可以表示为：y = f(x, β) + ε其中，f(x, β)是关于自变量x和参数向量β的函数，ε是误差项。

根据最小二乘法的原理，我们需要最小化残差平方和:RSS(β) = Σ(y - f(x, β))^22. 最小二乘法的求解过程为了找到使得残差平方和最小的参数向量β，我们需要对该函数进行求导，并令导数为零。

首先，我们定义一个矩阵X，该矩阵的每一行表示一个观测数据的自变量，每一列表示一个参数。

类似地，我们定义一个向量y，其中每个元素对应一个观测数据的因变量。

拟合曲线可表示为：y = Xβ + ε将这个表达式代入残差平方和的公式中，得到：RSS(β) = (y - Xβ)T(y - Xβ)我们的目标是找到一个参数向量β，使得RSS最小化。

使用微积分的方法，我们可以对RSS进行求导，得到：∂RSS(β) / ∂β = -2X^T(y - Xβ) = 0通过上述求导结果，我们可以解得最小二乘法的估计量β的闭式解为：β = (X^TX)^(-1)X^Ty3. 应用示例让我们通过一个简单的线性回归示例来演示最小二乘法的应用。

假设我们有以下观测数据：x = [1, 2, 3, 4, 5]y = [2, 4, 5, 4, 5]我们希望通过最小二乘法来拟合一个线性模型y = β0 + β1x。

首先，我们将数据转换为矩阵形式：X = [[1, 1], [1, 2], [1, 3], [1, 4], [1, 5]]y = [[2], [4], [5], [4], [5]]接下来，我们可以计算参数向量β：β = (X^TX)^(-1)X^Ty计算过程如下：X^TX = [[5, 15], [15, 55]](X^TX)^(-1) = [[11, -3], [-3, 1]]X^Ty = [[20], [70]]将上述结果代入β的公式，即可计算得到具体的参数值：β = [[11, -3], [-3, 1]] * [[20], [70]] = [[1.1818], [3.2727]]因此，最小二乘法拟合出的线性模型为：y = 1.1818 + 3.2727x通过该模型，我们可以预测其他自变量对应的因变量的值。

最小二乘法的原理及其应用1. 最小二乘法的原理最小二乘法是一种常用的数学优化方法，其原理是通过最小化残差平方和来寻找数据的最佳拟合线或曲线。

当数据存在随机误差时，最小二乘法可以有效地估计模型参数。

最小二乘法的基本原理可以概括为以下几个步骤：1.首先，假设模型的形式，如线性模型：y=mx+b。

2.然后，定义一个衡量模型拟合程度的误差函数，通常采用残差的平方和：$E(m, b) = \\sum_{i=1}^{n} (y_i - (mx_i + b))^2$。

3.接下来，根据最小二乘法的原理，我们需要通过对误差函数求偏导数，得出使误差函数最小化的模型参数。

4.最后，通过优化算法，如梯度下降法等，迭代地调整模型参数，使误差函数达到最小值，从而获得最佳拟合模型。

最小二乘法的原理非常简单和直观，因此被广泛应用于各个领域，如统计学、经济学、工程学等。

2. 最小二乘法的应用最小二乘法在实际问题中有着广泛的应用，下面将介绍其中的几个应用场景。

2.1 线性回归线性回归是最小二乘法最常见的应用之一。

在线性回归中，最小二乘法用于估计自变量与因变量之间的线性关系。

通过最小化残差平方和，我们可以找到一条最佳拟合直线，从而对未知的因变量进行预测。

线性回归广泛应用于经济学、社会学等领域，帮助研究者探索变量之间的相互关系。

2.2 曲线拟合最小二乘法还可以用于曲线拟合。

当我们需要拟合一个非线性模型时，可以通过最小二乘法来估计参数。

通过选择适当的模型形式和误差函数，可以得到最佳拟合曲线，从而准确地描述数据的变化趋势。

曲线拟合在信号处理、图像处理等领域具有重要的应用。

2.3 数据降维数据降维是指将高维度的数据转化为低维度表示，以便于可视化和分析。

最小二乘法可以用于主成分分析（PCA）等降维方法中。

通过寻找投影方向，使得在低维度空间中的数据点到其投影点的平均距离最小化，可以实现数据的有效降维。

2.4 系统辨识在控制工程中，最小二乘法经常被用于系统辨识。

题最小二乘法线性分类器设计目讲课老师：学生姓名：所属院系：专业: 学号:最小二乘法线性分类器设计1描述1.1最小二乘法原理的概述最小二乘法原理是指测量结果的最可信赖值应在残余误差平方和为最小的条件下求出。

从几何意义上讲，就是寻求与给定点(X j,yj (i=0,1,…,m)的距离平方和为最小的曲线y = p(x)。

函数p(x)称为拟合函数或最小二乘解，求拟合函数p(x)的方法称为曲线拟合的最小二乘法。

1.2最小二乘法的基本原理最小二乘法又称曲线拟合，所谓“拟合”即不要求所作的曲线完全通过所有的数据点，只要求所得的曲线能反映数据的基本趋势。

曲线拟合的几何解释：求一条曲线，使数据点均在离此曲线的上方或下方不远处。

从整体上考虑近似函数p(x)同所给数据点(X i, y i) (i=0,1, III，m)误差n = p(xj - y i (i =0,1,||( ,m)的大小，常用的方法有以下三种：一是误差r j=p(x)—y i (i=0,1」|(,m)绝对值的最大值max斤，即误差向量1g①mr =(r o,rj||,r m)T的范数；二是误差绝对值的和送斤|，即误差向量r的1—范数；三i=0m是误差平方和v『的算术平方根，即误差向量r的2—范数；前两种方法简单、自然，但i =0不便于微分运算，后一种方法相当于考虑2—范数的平方，因此在曲线拟合中常采用误差m平方和〔二『来度量误差r i(i=0 , 1，…，m)的整体大小。

i =0数据拟合的具体作法是：对给定数据(x，yJ (i=0,1,…，m),在取定的函数类①中，求p(x)・：•：」,使误差斤=p(X i)- y i (i=0,1,…,m)的平方和最小，即m m2'『八［p(xj -yj 二mini =0 i =0从几何意义上讲，就是寻求与给定点(X i,yj (i=0,1,…,m)的距离平方和为最小的曲线y = p(x)(图1)。

函数p(x)称为拟合函数或最小二乘解，求拟合函数p(x)的方法称为曲线拟合的最小二乘法。

4.最小二乘法线性拟合（非常好）我们知道，用作图法求出直线的斜率a 和截据b ，可以确定这条直线所对应的经验公式，但用作图法拟合直线时，由于作图连线有较大的随意性，尤其在测量数据比较分散时，对同一组测量数据，不同的人去处理，所得结果有差异，因此是一种粗略的数据处理方法，求出的a 和b 误差较大。

用最小二乘法拟合直线处理数据时,任何人去处理同一组数据，只要处理过程没有错误，得到的斜率a 和截据b 是唯一的。

最小二乘法就是将一组符合Y=a+bX 关系的测量数据，用计算的方法求出最佳的a 和b 。

显然，关键是如何求出最佳的a 和b 。

(1) 求回归直线设直线方程的表达式为：bx a y += (2-6-1)要根据测量数据求出最佳的a 和b 。

对满足线性关系的一组等精度测量数据（x i ，y i ），假定自变量x i 的误差可以忽略，则在同一x i 下，测量点y i 和直线上的点a+bx i 的偏差d i 如下：111bx a y d --=222bx a y d --=n n n bx a y d --=显然最好测量点都在直线上（即d 1=d 2=……=d n =0），求出的a 和b 是最理想的，但测量点不可能都在直线上，这样只有考虑d 1、d 2、……、d n 为最小，也就是考虑d 1+d 2+……+d n 为最小，但因d 1、d 2、……、d n 有正有负，加起来可能相互抵消，因此不可取；而|d 1|+|d 2|+……+ |d n |又不好解方程，因而不可行。

现在采取一种等效方法：当d 12+d 22+……+d n2对a 和b 为最小时，d 1、d 2、……、d n 也为最小。

取（d 12+d 22+……+d n 2）为最小值，求a 和b 的方法叫最小二乘法。

令 ∑==ni idD 12＝2112][i i ni ni ib a y dD --==∑∑== (2-6-2)D 对a 和b 分别求一阶偏导数为：][211∑∑==---=∂∂ni i n i i x b na y a D][21211∑∑∑===---=∂∂n i i n i i n i i i x b x a y x b D再求二阶偏导数为：n a D 222=∂∂； ∑==∂∂ni i x b D 12222 显然： 0222≥=∂∂n a D ； 021222≥=∂∂∑=n i i x b D 满足最小值条件，令一阶偏导数为零：011=--∑∑==ni i ni ix b na y(2-6-3)01211=--∑∑∑===ni i ni i ni ii x b x a yx (2-6-4)引入平均值： ∑==ni i x n x 11； ∑==n i i y n y 11；∑==n i i x n x 1221； ∑==ni i i y x n xy 11则： 0=--x b a y02=--x b x a xy （2-6-5） 解得： x b y a -= （2-6-6）22xx y x xy b --=（2-6-7）将a 、b 值带入线性方程bx a y +=，即得到回归直线方程。

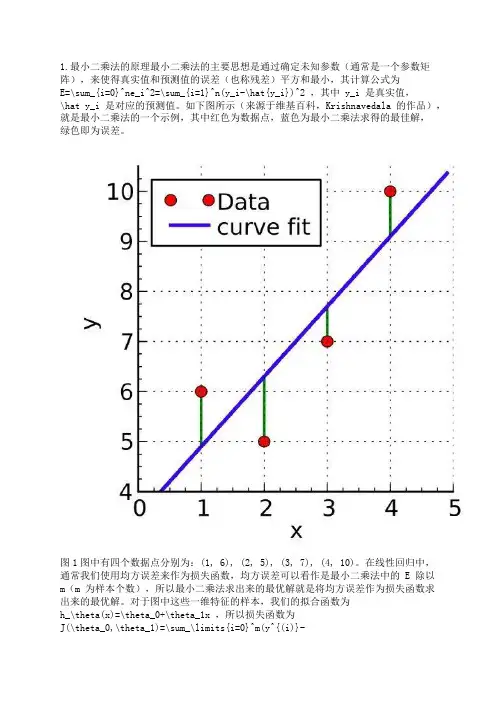
1.最小二乘法的原理最小二乘法的主要思想是通过确定未知参数（通常是一个参数矩阵），来使得真实值和预测值的误差（也称残差）平方和最小，其计算公式为E=\sum_{i=0}^ne_i^2=\sum_{i=1}^n(y_i-\hat{y_i})^2 ，其中 y_i 是真实值，\hat y_i 是对应的预测值。

如下图所示（来源于维基百科，Krishnavedala 的作品），就是最小二乘法的一个示例，其中红色为数据点，蓝色为最小二乘法求得的最佳解，绿色即为误差。

图1图中有四个数据点分别为：(1, 6), (2, 5), (3, 7), (4, 10)。

在线性回归中，通常我们使用均方误差来作为损失函数，均方误差可以看作是最小二乘法中的 E 除以m（m 为样本个数），所以最小二乘法求出来的最优解就是将均方误差作为损失函数求出来的最优解。

对于图中这些一维特征的样本，我们的拟合函数为h_\theta(x)=\theta_0+\theta_1x ，所以损失函数为J(\theta_0,\theta_1)=\sum_\limits{i=0}^m(y^{(i)}-h_\theta(x^{(i)}))^2=\sum_\limits{i=0}^m(y^{(i)}-\theta_0-\theta_1x^{(i)})^2 （这里损失函数使用最小二乘法，并非均方误差），其中上标(i)表示第 i 个样本。

2.最小二乘法求解要使损失函数最小，可以将损失函数当作多元函数来处理，采用多元函数求偏导的方法来计算函数的极小值。

例如对于一维特征的最小二乘法， J(\theta_0,\theta_1) 分别对 \theta_0 ， \theta_1 求偏导，令偏导等于 0 ，得：\frac{\partial J(\theta_0,\theta_1)}{\partial\theta_0}=-2\sum_\limits{i=1}^{m}(y^{(i)}-\theta_0-\theta_1x^{(i)}) =0\tag{2.1}\frac{\partial J(\theta_0,\theta_1)}{\partial\theta_1}=-2\sum_\limits{i=1}^{m}(y^{(i)}-\theta_0-\theta_1x^{(i)})x^{(i)} = 0\tag{2.2}联立两式，求解可得：\theta_0=\frac{\sum_\limits{i=1}^m(x^{(i)})^2\sum_\limits{i=1}^my^{(i)}-\sum_\limits{i=1}^mx^{(i)}\sum_\limits{i=1}^mx^{(i)}y^{(i)}}{m\sum_\limits{i=1}^m(x^{(i)})^2-(\sum_\limits{i=1}^mx^{(i)})^2} \tag{2.3}\theta_1=\frac{m\sum_\limits{i=1}^mx^{(i)}y^{(i)}-\sum_\limits{i=1}^mx^{(i)}\sum_\limits{i=1}^my^{(i)}}{m\sum_\limits{i=1}^m(x^{(i)})^2-(\sum_\limits{i=1}^mx^{(i)})^2} \tag{2.4}对于图 1 中的例子，代入公式进行计算，得： \theta_0 = 3.5, \theta_1=1.4,J(\theta) = 4.2 。

最小二乘法求解线性回归问题最小二乘法是回归分析中常用的一种模型估计方法。

它通过最小化样本数据与模型预测值之间的误差平方和来拟合出一个线性模型，解决了线性回归中的参数估计问题。

在本文中，我将详细介绍最小二乘法在线性回归问题中的应用。

一、线性回归模型在介绍最小二乘法之前，先了解一下线性回归模型的基本形式。

假设我们有一个包含$n$个观测值的数据集$(x_1,y_1),(x_2,y_2),\dots,(x_n,y_n)$，其中$x_i$表示自变量，$y_i$表示因变量。

线性回归模型的一般形式如下：$$y=\beta_0+\beta_1 x_1+\beta_2 x_2+\dots+\beta_px_p+\epsilon$$其中，$\beta_0$表示截距，$\beta_1,\beta_2,\dots,\beta_p$表示自变量$x_1,x_2,\dots,x_p$的系数，$\epsilon$表示误差项。

我们希望通过数据集中的观测值拟合出一个线性模型，即确定$\beta_0,\beta_1,\dots,\beta_p$这些未知参数的值，使得模型对未知数据的预测误差最小化。

二、最小二乘法的思想最小二乘法是一种模型拟合的优化方法，其基本思想是通过最小化优化问题的目标函数来确定模型参数的值。

在线性回归问题中，我们通常采用最小化残差平方和的方式来拟合出一个符合数据集的线性模型。

残差代表观测值与模型估计值之间的差异。

假设我们有一个数据集$(x_1,y_1),(x_2,y_2),\dots,(x_n,y_n)$，并且已经选定了线性模型$y=\beta_0+\beta_1 x_1+\beta_2 x_2+\dots+\beta_p x_p$。

我们希望选择一组系数$\beta_0,\beta_1,\dots,\beta_p$，使得模型对数据集中的观测值的预测误差最小，即最小化残差平方和（RSS）：$$RSS=\sum_{i=1}^n(y_i-\hat{y}_i)^2$$其中，$y_i$表示第$i$个观测值的实际值，$\hat{y}_i$表示该观测值在当前模型下的预测值。

利用最小二乘法求线性回归方程最小二乘法的线性回归方程是一种常用的统计分析方法，其用于描述两变量之间的依赖关系，这些变量可以是连续或离散类型的。

线性回归方程可以用来估计目标变量，预测特定的输入变量，或者预测一组输入变量的相互作用。

最小二乘法可以用来拟合线性回归模型，以获得最佳的拟合结果。

最小二乘法的线性回归模型需要一个因变量和至少一个自变量来构建拟合曲线。

因变量是拟合曲线的响应变量，而自变量是因变量的驱动变量。

最小二乘法确定一条最佳拟合线，该拟合线可以使响应变量与自变量之间的误差最小。

最小二乘法可以用来拟合一维、二维或多维线性回归方程。

一维线性回归模型由以下线性方程所确定：y = aX + b其中，a为斜率，b为原点。

X表示自变量，y表示因变量，而a 和b表示拟合曲线的参数。

最小二乘法可以用来求解拟合曲线参数a 和b，从而拟合一维线性回归模型。

二维线性回归模型由以下线性方程所确定：y = aX1 + bX2 + c其中，X1和X2分别为两个自变量，y表示因变量，而a、b和c 表示拟合曲线的参数。

最小二乘法可以用来求解拟合曲线参数a、b 和c，从而拟合二维线性回归模型。

多维线性回归模型由以下线性方程所确定：y = aX1 + bX2 + cX3 ++ z其中，X1、X2、X3、…Z分别为多个自变量，y表示因变量，而a、b、c、…z表示拟合曲线的参数。

最小二乘法可以用来求解拟合曲线参数a、b、c、…z，从而拟合多维线性回归模型。

最小二乘法可以用来求解拟合曲线参数的最优值，从而得到最佳的拟合效果。

它的原理是：最小二乘法估计公式参数使得残差平方和最小，残差即为实际值和拟合值之差。

通过最小二乘法拟合方程，计算出不同变量之间的回归系数，以衡量变量之间的相互依赖性，以及拟合曲线的准确程度。

最小二乘法线性回归方程可以有效地用于统计分析，以了解变量之间的依赖关系。

它可以用来估算目标变量，预测特定的输入变量，以及预测一组输入变量的相互作用。

最小二乘法的公式最小二乘法是一种常用的回归分析方法，用来寻找一个线性模型来拟合给定的数据。

最小二乘法的目标是最小化实际数据与拟合模型之间的残差平方和，即找到使得残差平方和最小的系数。

在回归分析中，最小二乘法是一种经典的统计学方法，有着广泛的应用。

一般来说，给定一个数据集，我们需要找到一个线性模型，使得该模型能最好地拟合这些数据。

这个线性模型可以通过最小二乘法来求解，具体的公式如下：1. 线性模型公式假设我们的数据集包含了n个样本数据，每个数据由p个特征和一个目标变量组成。

我们可以将每个样本数据表示为一个向量，并将这些向量组合成一个矩阵X，其中X的维度是n x p，n为样本数量，p为特征数量。

我们的目标是找到一个系数向量β，使得线性模型的预测值与实际值之间的残差平方和最小。

我们用y表示实际值，用Xβ表示线性模型的预测值，残差向量为ε = y - Xβ。

2. 残差平方和的最小化为了最小化残差平方和，我们需要最小化ε的平方和。

我们可以用L2范数（欧氏距离）来度量残差向量的长度，即我们的目标是最小化||ε||^2。

所以，我们的最小二乘法的公式可以表述为：min ||ε||^2 = min (y - Xβ)^T(y - Xβ)为了求解这个最小化问题，我们需要计算残差平方和的导数，并令导数为0，从而找到导数为0时的系数β。

3. 求解最小二乘法的一般公式求解最小二乘法的公式可以通过求导的方式来推导，具体的推导过程比较繁琐，这里我们直接给出最后的结果。

设关于β的残差平方和为F(β)，则我们需要求解的最优解β的一般公式为：∂F(β)/∂β = -2X^T(y - Xβ) = 0整理方程，我们可以得到最小二乘法的一般公式：X^T(y - Xβ) = 0我们可以进一步解这个等式，求得β的一般解：β = (X^TX)^(-1)X^Ty其中，(X^TX)^(-1)表示X^TX的逆矩阵。

通过这个公式，我们可以计算出最小二乘法的系数β，从而得到拟合数据的线性模型。

最小二乘法线性与非线性拟合最小二乘法实现数据拟合最小二乘法原理函数插值是差值函数p(x)与被插函数f(x)在节点处函数值相同，即p( )=f( ) (i=0,1,2,3……,n)，而曲线拟合函数不要求严格地通过所有数据点( )，也就是说拟合函数在处的偏差=不都严格地等于零。

但是，为了使近似曲线能尽量反应所给数据点的变化趋势，要求| |按某种度量标准最小。

即=为最小。

这种要求误差平方和最小的拟合称为曲线拟合的最小二乘法。

(一)线性最小二乘拟合根据线性最小二乘拟合理论，我们得知关于系数矩阵A的解法为A＝R\Y。

例题假设测出了一组，由下面的表格给出，且已知函数原型为y(x)=c1+c2*e^(-3*x)+c3*cos(-2*x)*exp(-4*x)+c4*x^2试用已知数据求出待定系数的值。

在Matlab中输入以下程序x=[0,0.2,0.4,0.7,0.9,0.92,0.99,1.2,1.4,1.48,1.5]';y=[2.88;2.2576;1.9683;1.9258;2.0862;2.109;2.1979;2.5409;2.9627;3.155;3.2052];A=[ones(size(x)) exp(-3*x),cos(-2*x).*exp(-4*x) x.^2];c=A\y;c'运行结果为ans =1.22002.3397 -0.6797 0.8700下面画出由拟合得到的曲线及已知的数据散点图x1=[0:0.01:1.5]';A1=[ones(size(x1)) exp(-3*x1),cos(-2*x1).*exp(-4*x1) x1.^2]; y1=A1*c;plot(x1,y1,x,y,'o')事实上，上面给出的数据就是由已知曲线y(x)= 0.8700-0.6797*e^(-3*x)+ 2.3397*cos(-2*x)*exp(-4*x)+1.2200*x^2产生的，由上图可见拟合效果较好。

线性回归——最⼩⼆乘法（⼀）相信学过数理统计的都学过线性回归（linear regression），本篇⽂章详细将讲解单变量线性回归并写出使⽤最⼩⼆乘法（least squares method）来求线性回归损失函数最优解的完整过程，⾸先推导出最⼩⼆乘法，后⽤最⼩⼆乘法对⼀个简单数据集进⾏线性回归拟合；线性回归 线性回归假设数据集中特征与结果存在着线性关系； 等式：y = mx + c y为结果，x为特征，m为系数，c为误差在数学中m为梯度c为截距 这个等式为我们假设的，我们需要找到m、c使得mx+c得到的结果与真实的y误差最⼩，这⾥使⽤平⽅差来衡量估计值与真实值得误差（如果只⽤差值就可能会存在负数）；⽤于计算真实值与预测值的误差的函数称为：平⽅损失函数（squard loss function）；这⾥⽤L表⽰损失函数，所以有： 整个数据集上的平均损失为： 我们要求得最匹配的m与c使得L最⼩；数学表达式可以表⽰为： 最⼩⼆乘法⽤于求⽬标函数的最优值，它通过最⼩化误差的平⽅和寻找匹配项所以⼜称为：最⼩平⽅法；这⾥将⽤最⼩⼆乘法⽤于求得线性回归的最优解；最⼩⼆乘法 为了⽅便讲清楚最⼩⼆乘法推导过程这⾥使⽤，数据集有1…N个数据组成，每个数据由、构成，x表⽰特征，y为结果；这⾥将线性回归模型定义为：平均损失函数定义有： 要求得L的最⼩，其关于c与m的偏导数定为0，所以求偏导数，得出后让导数等于0，并对c与m求解便能得到最⼩的L此时的c与m便是最匹配该模型的；关于c偏导数：因为求得是关于c的偏导数，因此把L的等式中不包含c的项去掉得：整理式⼦把不包含下标n的往累加和外移得到：对c求偏导数得：关于m的偏导数：求关于m的偏导数，因此把L等式中不包含项去掉得： 整理式⼦把不包含下标n的往累加和外移得到：对m求偏导数得：令关于c的偏导数等于0，求解：从上求解得到的值可以看出，上⾯式⼦中存在两个平均值，因此该等式也可以改写成：令关于m的偏导数等于0，求解： 关于m的偏导数依赖于c，⼜因为已经求得了关于c偏导数的解，因此把求关于c偏导数的解代数关于m的偏导数式⼦得：合并含有m的项化简：求解：为了简化式⼦，再定义出：⽰例：这⾥使⽤上⾯得到的最⼩⼆乘法公式对以下数据集进⾏线性拟合：n x y xy x^212484268483639121088141321273169平均值7.511.25109.2572.5数据点分布情况：根据上诉最⼩⼆乘法公式计算出当前数据集最优：m与cc = 11.25 - 1.5307 * 7.5 = -0.23最后得出当前线性函数为：y = 1.5307x - 0.23计算出每个节点的预测值：y1 = 1.5307 * 2 - 0.23 = 2.83y2 = 1.5307 * 6 - 0.23 = 8.9542y3 = 1.5307 * 9 - 0.23 = 13.5463y4 = 1.5307 * 13- 0.23 = 19.6691拟合结果：参考资料：a first course in machine learning⽂章⾸发地址：。