用最小二乘法求线性回归方程

⼀元线性回归的最⼩⼆乘法详解及代码。

个⼈记录，⼤部分摘⾃概率论与数理统计⼀元线性回归模型设y与x间有相关关系，称x为⾃变量，y为因变量，我们只考虑在x是可控变量，只有y是随机变量，那么他们之间的相关关系可以表⽰为y=f(x)+ε其中ε是随机误差，⼀般假设ε~N（0，σ2）。

由于ε是随机变量，导致y也是随机变量。

进⾏回归分析⾸先是回归函数形式的选择。

通常采⽤画散点图来进⾏选择。

有⼀份合⾦钢强度y与碳含量x的数据表数据散点图如下可以看出，数据点基本在⼀条直线上，说明两个数据有线性相关关系，可以表⽰为y=β0+β1x+ε这是y关于x的⼀元线性回归的数据结构，其中β0，β1分别是截距和斜率。

ε~N(0,σ2)则回归⽅程为回归系数的最⼩⼆乘法估计。

我们⾸先令偏差平⽅和Q（β0，β1）=∑n i=1(y i-β0-β1x i)2最⼩⼆乘法就是尽量使Q（β0，β1）=∑n i=1(y i-β0-β1x i)2=0，分别对β0，β1求偏导整理后可知⽅程组 1如⽆特殊声明Σ均表⽰Σn i=1，则有解⽅程组1 可知python代码1import numpy as np2#导⼊回归数据3 x=np.array([0.1,0.11,0.12,0.13,0.14,0.15,0.16,0.17,0.18,0.2,0.21,0.23])4 y=np.array([42,43,45,45,45,47.5,49,53,50,55,55,60])5#x求和6 sx=sum(x)7# y求和8 sy=sum(y)9#参数个数10 n=len(x)11#x的平均值12 mx=np.mean(x)13#y的平均值14 my=np.mean(y)15#∑(xi)^2,所有xi的平⽅和16 sx2=sum(x*x)17#∑(yi)^2所有yi的平⽅和18 sy2=sum(y*y)19#∑xiyi 所有xiyi的和20 sxy=sum(x*y)21#lxx22 lxx=sx2-1/n*pow(sx,2)23#lxy24 lxy=sxy-1/n*sx*sy25#lyy26 lyy=sy2-1/n*pow(sy,2)27#β128β1=lxy/lxx29#β030β0=my-mx*β13132#结果 y=28.08+132.90到此结束。

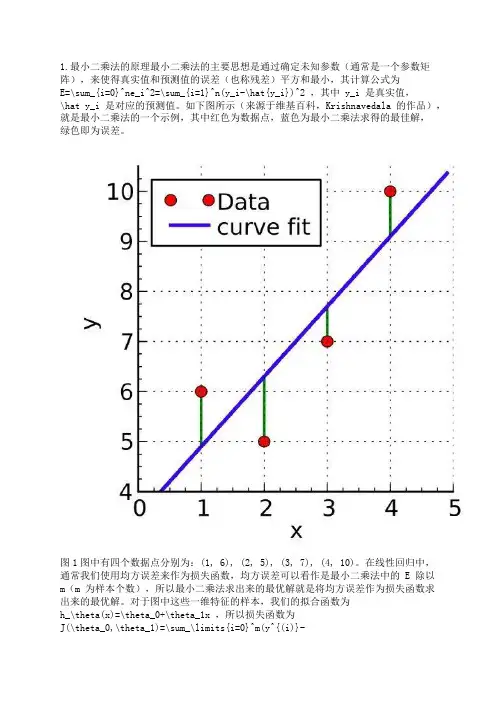
1.最小二乘法的原理最小二乘法的主要思想是通过确定未知参数（通常是一个参数矩阵），来使得真实值和预测值的误差（也称残差）平方和最小，其计算公式为E=\sum_{i=0}^ne_i^2=\sum_{i=1}^n(y_i-\hat{y_i})^2 ，其中 y_i 是真实值，\hat y_i 是对应的预测值。

如下图所示（来源于维基百科，Krishnavedala 的作品），就是最小二乘法的一个示例，其中红色为数据点，蓝色为最小二乘法求得的最佳解，绿色即为误差。

图1图中有四个数据点分别为：(1, 6), (2, 5), (3, 7), (4, 10)。

在线性回归中，通常我们使用均方误差来作为损失函数，均方误差可以看作是最小二乘法中的 E 除以m（m 为样本个数），所以最小二乘法求出来的最优解就是将均方误差作为损失函数求出来的最优解。

对于图中这些一维特征的样本，我们的拟合函数为h_\theta(x)=\theta_0+\theta_1x ，所以损失函数为J(\theta_0,\theta_1)=\sum_\limits{i=0}^m(y^{(i)}-h_\theta(x^{(i)}))^2=\sum_\limits{i=0}^m(y^{(i)}-\theta_0-\theta_1x^{(i)})^2 （这里损失函数使用最小二乘法，并非均方误差），其中上标(i)表示第 i 个样本。

2.最小二乘法求解要使损失函数最小，可以将损失函数当作多元函数来处理，采用多元函数求偏导的方法来计算函数的极小值。

例如对于一维特征的最小二乘法， J(\theta_0,\theta_1) 分别对 \theta_0 ， \theta_1 求偏导，令偏导等于 0 ，得：\frac{\partial J(\theta_0,\theta_1)}{\partial\theta_0}=-2\sum_\limits{i=1}^{m}(y^{(i)}-\theta_0-\theta_1x^{(i)}) =0\tag{2.1}\frac{\partial J(\theta_0,\theta_1)}{\partial\theta_1}=-2\sum_\limits{i=1}^{m}(y^{(i)}-\theta_0-\theta_1x^{(i)})x^{(i)} = 0\tag{2.2}联立两式，求解可得：\theta_0=\frac{\sum_\limits{i=1}^m(x^{(i)})^2\sum_\limits{i=1}^my^{(i)}-\sum_\limits{i=1}^mx^{(i)}\sum_\limits{i=1}^mx^{(i)}y^{(i)}}{m\sum_\limits{i=1}^m(x^{(i)})^2-(\sum_\limits{i=1}^mx^{(i)})^2} \tag{2.3}\theta_1=\frac{m\sum_\limits{i=1}^mx^{(i)}y^{(i)}-\sum_\limits{i=1}^mx^{(i)}\sum_\limits{i=1}^my^{(i)}}{m\sum_\limits{i=1}^m(x^{(i)})^2-(\sum_\limits{i=1}^mx^{(i)})^2} \tag{2.4}对于图 1 中的例子，代入公式进行计算，得： \theta_0 = 3.5, \theta_1=1.4,J(\theta) = 4.2 。

“最小二乘法求线性回归方程”教学设计一．内容和内容解析本节课的主要内容为用最小二乘法求线性回归方程。

本节课内容作为上节课线性回归方程探究的知识发展，在知识上有很强的联系，所以，核心概念还是回归直线。

在“经历用不同估算方法描述两个变量线性相关关系”的过程后，解决好用数学方法刻画“从整体上看，各点与此直线的距离最小”，让学生在此基础上了解更为科学的数据处理方式——最小二乘法，有助于更好的理解核心概念，并最终体现回归方法的应用价值。

就统计学科而言，对不同的数据处理方法进行“优劣评价”是“假设检验”的萌芽，而后者是统计学学科研究的另一重要领域。

了解“最小二乘法思想”，比较各种“估算方法”，体会它的相对科学性，既是统计学教学发展的需要，又在体会此思想的过程中促进了学生对核心概念的进一步理解。

“最小二乘法思想”作为本节课的核心思想，由此得以体现。

而回归思想和贯穿统计学科中的随机思想，也在本节课中需有所渗透。

所以，在内容重点的侧重上，本节课与上节课有较大的区别：上节课侧重于估算方法设计，在不同的数据处理过程中，体会回归直线作为变量相关关系代表这一概念特征；本节课侧重于估算方法评价与实际应用，在评价中使学生体会核心思想，理解核心概念。

考虑到本节课的教学侧重点与新课程标准的要求，对线性回归方程系数的计算公式，可直接给出。

由于公式的复杂性，一方面，既要通过教学设计合理体现知识发生过程，不搞“割裂”；另一方面，要充分利用计算机或计算器，简化繁琐的求解系数过程，简化过于形式化的证明说理过程。

基于上述内容分析，确定本节课的教学重点为知道最小二乘法思想，并能根据给出的线性回归方程的系数公式建立线性回归方程。

二．目标和目标解析本节课要求学生了解最小二乘法思想，掌握根据给出的线性回归方程系数公式建立线性回归方程，理解线性回归方程概念和回归思想，在以上过程中体会随机思想：1．能用数学符号刻画出“从整体上看，各点与此直线的点的偏差”的表达方式；2．通过减少样本点个数，经历对表达式的展开，把“偏差最小”简化为“二次多项式”最小值问题，通过合情推理，使学生接受最小二乘法的科学性，在此过程中了解最小二乘法思想；3．能结合具体案例，经历数据处理步骤，根据回归方程系数公式建立回归方程；4．通过改变同一问题下样本点的选择进而对照回归方程的差异，体会随机思想；5．利用回归方程预测，体现用“确定关系研究相关关系”的回归思想；三．教学目标分析在经历用不同估算方法描述两个变量线性相关的过程后，在学生现有知识能力范围内，如何选择一个最优方法，成为知识发展的逻辑必然。

最小二乘法求解线性回归问题最小二乘法是回归分析中常用的一种模型估计方法。

它通过最小化样本数据与模型预测值之间的误差平方和来拟合出一个线性模型，解决了线性回归中的参数估计问题。

在本文中，我将详细介绍最小二乘法在线性回归问题中的应用。

一、线性回归模型在介绍最小二乘法之前，先了解一下线性回归模型的基本形式。

假设我们有一个包含$n$个观测值的数据集$(x_1,y_1),(x_2,y_2),\dots,(x_n,y_n)$，其中$x_i$表示自变量，$y_i$表示因变量。

线性回归模型的一般形式如下：$$y=\beta_0+\beta_1 x_1+\beta_2 x_2+\dots+\beta_px_p+\epsilon$$其中，$\beta_0$表示截距，$\beta_1,\beta_2,\dots,\beta_p$表示自变量$x_1,x_2,\dots,x_p$的系数，$\epsilon$表示误差项。

我们希望通过数据集中的观测值拟合出一个线性模型，即确定$\beta_0,\beta_1,\dots,\beta_p$这些未知参数的值，使得模型对未知数据的预测误差最小化。

二、最小二乘法的思想最小二乘法是一种模型拟合的优化方法，其基本思想是通过最小化优化问题的目标函数来确定模型参数的值。

在线性回归问题中，我们通常采用最小化残差平方和的方式来拟合出一个符合数据集的线性模型。

残差代表观测值与模型估计值之间的差异。

假设我们有一个数据集$(x_1,y_1),(x_2,y_2),\dots,(x_n,y_n)$，并且已经选定了线性模型$y=\beta_0+\beta_1 x_1+\beta_2 x_2+\dots+\beta_p x_p$。

我们希望选择一组系数$\beta_0,\beta_1,\dots,\beta_p$，使得模型对数据集中的观测值的预测误差最小，即最小化残差平方和（RSS）：$$RSS=\sum_{i=1}^n(y_i-\hat{y}_i)^2$$其中，$y_i$表示第$i$个观测值的实际值，$\hat{y}_i$表示该观测值在当前模型下的预测值。

最小二乘法与回归分析最小二乘法是回归分析中最常用的方法之一、通过这种方法，可以找到最佳拟合曲线以描述自变量和因变量之间的关系。

最小二乘法通过最小化误差平方和来确定最佳拟合线。

本文将详细介绍最小二乘法和回归分析的概念、原理和应用。

回归分析是一种统计方法，用于确定两个或多个变量之间的关系。

在回归分析中，通常将一个变量定义为因变量，而其他变量则成为自变量，因为它们被认为是影响因变量的因素。

回归分析的目标是建立一个数学模型来描述因变量和自变量之间的关系。

回归模型通常采用线性方程的形式，可以通过拟合数据点来确定最佳拟合线。

最小二乘法是一种估计参数的方法，用于确定最佳拟合线。

最小二乘法的基本原理是通过最小化残差平方和来确定最佳拟合线。

残差是因变量与回归线之间的垂直距离。

残差平方和表示所有数据点与回归线之间的差异的平方和。

通过最小化残差平方和，可以找到最佳拟合线，使得残差达到最小。

在线性回归分析中，通过最小二乘法可以确定回归线的斜率和截距。

斜率表示因变量在自变量变化一个单位时的变化率，截距表示当自变量为零时的因变量的值。

通过求解最小二乘方程求出斜率和截距的估计值，从而得到回归线的方程。

最小二乘法还可以用于评估回归模型的拟合程度。

通过计算拟合优度和均方根误差，可以判断回归模型的预测能力。

拟合优度是一个介于0和1之间的值，表示因变量的变异程度中可以由自变量解释的比例。

均方根误差衡量了回归模型的预测误差的平均大小。

在实际应用中，最小二乘法和回归分析广泛应用于各个领域。

例如，在经济学中，最小二乘法可以用于分析消费者支出和收入之间的关系；在医学中，最小二乘法可以用于探索药物剂量和治疗效果之间的关系。

最小二乘法还可以用于时间序列分析、预测和趋势分析等领域。

总之，最小二乘法是回归分析中最常用的方法之一、通过最小化残差平方和，可以确定最佳拟合线并评估回归模型的拟合程度。

最小二乘法在实际应用中具有广泛的应用领域，可以帮助我们了解和解释变量之间的关系。

加权最小二乘法推导加权最小二乘法，是一种常用的线性回归分析方法，也是数理统计学中重要的一种最小二乘法拟合方法。

它的基本思想是对回归模型的误差进行加权处理，以获得更准确的拟合结果。

在传统的最小二乘法中，对于线性回归模型 $Y = \beta_0 +\beta_1X$，我们试图通过最小化残差平方和 $\sum_{i=1}^{n}(Y_i - (\beta_0 + \beta_1X_i))^2$ 来拟合最优的回归系数 $\beta_0$ 和$\beta_1$，其中$n$代表样本数量。

然而，在实际应用中，每个观测样本的重要性往往是不同的，而传统最小二乘法对每个样本的重要性均等看待，这样可能导致某些重要样本的误差被较不重要的样本的误差所掩盖。

为了解决这个问题，引入加权最小二乘法。

其核心思想是为每个样本分配一个权重，以便强调重要样本的贡献，削弱不重要样本的影响。

假设观测值的权重为 $w_i$，则加权最小二乘法的目标是最小化加权残差平方和 $S = \sum_{i=1}^{n} w_i(Y_i - (\beta_0 +\beta_1X_i))^2$。

接下来，我们通过最小化$S$来求解回归系数。

首先，我们对$\beta_0$ 和 $\beta_1$ 分别求导，令导数为零，可以得到以下正规方程组：$$\begin{cases}\sum_{i=1}^{n} w_iY_i = \beta_0\sum_{i=1}^{n} w_i +\beta_1\sum_{i=1}^{n} w_iX_i\\\sum_{i=1}^{n} w_iY_iX_i = \beta_0\sum_{i=1}^{n} w_iX_i + \beta_1\sum_{i=1}^{n} w_iX_i^2\end{cases}$$通过解这个方程组，我们可以得到回归系数的估计值$\hat{\beta_0}$ 和 $\hat{\beta_1}$。

进而，利用这两个估计值，我们可以得到拟合方程为 $\hat{Y} = \hat{\beta_0} +\hat{\beta_1}X$。