15随机事件的独立性

随机事件的独立性与互斥性知识点随机事件是指在一定的条件下，可能发生也可能不发生的事件。

在概率论中，研究随机事件之间的关系非常重要，其中独立性与互斥性是两个基本概念。

本文将介绍随机事件的独立性与互斥性的定义、性质以及在实际问题中的应用。

一、独立事件的定义与性质独立事件是指两个或多个事件发生的结果不会相互影响的事件。

具体来说，如果事件 A 和事件 B 是独立事件，那么事件 A 的发生与否不会对事件 B 的发生产生影响，反之亦然。

独立事件的性质如下：1. 乘法公式：对于两个独立事件 A 和 B，它们同时发生的概率等于它们分别发生的概率之积，即P(A∩B) = P(A) × P(B)。

2. 加法公式：对于两个独立事件 A 和 B，它们至少有一个发生的概率等于它们分别发生的概率之和减去它们同时发生的概率，即P(A∪B) = P(A) + P(B) - P(A∩B)。

独立事件的性质保证了事件之间的独立性，使得我们可以通过简单的计算得到复杂事件的概率。

二、互斥事件的定义与性质互斥事件是指两个事件不可能同时发生的事件。

具体来说，如果事件 A 和事件 B 是互斥事件，那么事件 A 的发生就排除了事件 B 的发生，反之亦然。

互斥事件的性质如下：1. 加法公式：对于两个互斥事件 A 和 B，它们至少有一个发生的概率等于它们分别发生的概率之和，即 P(A∪B) = P(A) + P(B)。

互斥事件的性质使得我们可以通过计算事件的发生概率，确定事件之间的关系，从而进行合理的判断和决策。

三、独立事件与互斥事件的区别与联系独立事件和互斥事件都是描述随机事件之间关系的概念，但它们的定义和性质有所不同。

1. 独立事件是指两个或多个事件的发生结果不会相互影响，而互斥事件是指两个事件不可能同时发生。

2. 独立事件的加法公式和乘法公式可以用于计算独立事件的概率，而互斥事件只需要使用加法公式就可以计算。

独立事件和互斥事件在实际问题中有着广泛的应用。

判断随机事件独立性的方法随机事件独立性是概率论与数理统计中的一个重要概念。

判断随机事件是否独立对于许多实际问题的解决具有重要意义。

本文将介绍判断随机事件独立性的方法及其应用。

1. 什么是随机事件独立性在概率论中，独立性是指两个或多个事件的发生不受彼此影响的性质。

具体来说，如果事件A的发生与事件B的发生没有任何关联，即事件A的发生概率与事件B的发生概率的乘积等于事件A与B同时发生的概率，那么事件A和事件B就是独立的。

数学上，可以用以下条件来判断两个事件A和B是否独立： - P(A ∩ B) = P(A) * P(B)，即事件A与事件B同时发生的概率等于事件A的发生概率乘以事件B的发生概率。

2. 判断随机事件独立性的方法2.1. 基于条件概率的方法基于条件概率的方法是判断随机事件独立性的常用方法之一。

根据条件概率的定义，可以使用以下条件来判断两个事件A和B是否独立： - P(A|B) = P(A)，即事件A在事件B发生的条件下的概率等于事件A的概率。

如果满足以上条件，那么可以认为事件A和事件B是独立的。

否则，事件A 和事件B不满足独立性条件。

2.2. 基于频率统计的方法基于频率统计的方法是另一种常用的判断随机事件独立性的方法。

该方法基于大数定律，通过实际观察和统计事件发生的频率来判断事件之间是否独立。

具体操作时，可以进行一系列独立的实验，统计事件A和事件B同时发生的次数。

如果事件A和事件B的同时发生次数与事件A的发生次数乘以事件B的发生次数之积接近，那么可以认为事件A和事件B是独立的。

否则，事件A和事件B不满足独立性条件。

2.3. 基于协方差的方法基于协方差的方法是另一种常用的判断随机事件独立性的方法。

协方差是衡量两个随机变量之间关联程度的指标，可以通过计算事件A和事件B的协方差来判断它们是否独立。

具体操作时，可以通过以下条件来判断事件A和事件B是否独立： - 协方差(A, B) = 0，即事件A和事件B的协方差为0。

随机事件的独立性与条件概率随机事件是在一定条件下具有不确定性的事件，它的发生与否取决于一系列的因素。

而随机事件的独立性是指事件的发生与其他事件的发生无关，即一个事件的发生与其他事件的发生是相互独立的。

条件概率则是指在已知某个事件发生的条件下，另一个事件发生的概率。

1. 随机事件的独立性随机事件的独立性是指一个事件的发生与其他事件的发生无关。

具体来说，对于两个事件A和B，如果事件A的发生与否不会改变事件B的发生概率，那么事件A和事件B就是相互独立的。

例如，假设我们有一个袋子里面有红球和蓝球，事件A表示从袋子中取出一个红球，事件B表示从袋子中取出一个蓝球。

如果每次取球之前都将袋子中的球重新放回，那么事件A的发生与否不会改变事件B的发生概率，因此事件A和事件B是相互独立的。

2. 条件概率条件概率是指在已知某个事件发生的条件下，另一个事件发生的概率。

通常使用P(A|B)来表示在事件B发生的情况下事件A发生的概率。

例如，假设我们有一副扑克牌，事件A表示从中抽取一张黑桃，事件B表示从中抽取一张红心。

如果我们已知事件B发生，也就是已知从中抽取的牌是一张红心，那么事件A发生的概率就会发生变化。

因为已经抽出了一张红心，所以扑克牌中剩余的牌中，黑桃的比例就会减少，从而影响到事件A发生的概率。

3. 独立性与条件概率的关系独立性和条件概率是密切相关的概念。

如果事件A和事件B是相互独立的，那么在已知事件B发生的情况下，事件A的发生概率仍然保持不变，即P(A|B) = P(A)。

这是因为独立事件的发生与其他事件的发生无关，所以在已知事件B发生的情况下，不会对事件A的发生概率造成影响。

然而，如果事件A和事件B不是相互独立的，那么在已知事件B 发生的情况下，事件A的发生概率会发生变化，即P(A|B) ≠ P(A)。

这是因为事件B的发生会对事件A的发生概率产生影响，所以在已知事件B发生的情况下，事件A的发生概率会有所不同。

总结：随机事件的独立性与条件概率是概率论中重要的概念。

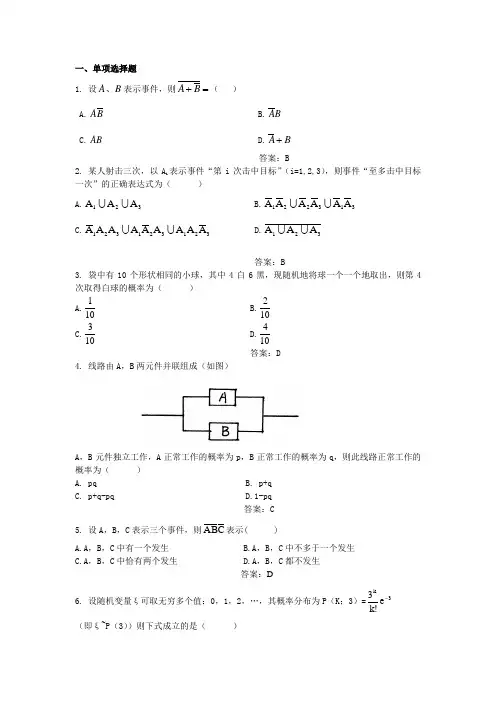
一、单项选择题1. 设B A 、表示事件，则=+B A （ ）A.B AB.B AC.ABD.B A +答案：B2. 某人射击三次，以A i 表示事件“第i 次击中目标”（i=1,2,3），则事件“至多击中目标一次”的正确表达式为（ ）A.321A A AB.313221A A A A A AC.321321321A A A A A A A A AD.321A A A答案：B3. 袋中有10个形状相同的小球，其中4白6黑，现随机地将球一个一个地取出，则第4次取得白球的概率为（ ）A.101 B.102C.103D.104 答案：D 4. 线路由A ，B 两元件并联组成（如图）A ，B 元件独立工作，A 正常工作的概率为p ，B 正常工作的概率为q ，则此线路正常工作的概率为（ ）A. pqB. p+qC. p+q-pqD.1-pq答案：C 5. 设A ，B ，C 表示三个事件，则C B A 表示( )A.A ，B ，C 中有一个发生B.A ，B ，C 中不多于一个发生C.A ，B ，C 中恰有两个发生D.A ，B ，C 都不发生答案：D6. 设随机变量ξ可取无穷多个值：0，1，2，…，其概率分布为P （K ；3）=3k e !k 3- （即ξ~P （3））则下式成立的是（ ）A.E ξ=D ξ=3B.E ξ=D ξ=31 C.E ξ=3，D ξ=31D.E ξ=31，D ξ=3 答案：A7. 设随机变量ξ的分布列为P{ξ=k}=Ak,k=1,2,3,4,5，则常数A=（ ） A.5 B.10C.15D.20答案：C 8. 设ξ的分布为则常数α=（ ） A.0.1B.0.2C.0.3D.0.4答案：A9. 设ζ的分布列为则E ζ2=( ) A.-0.2 B.0.2 C.2.76 D.2.8答案：D10. 设随机变量ξ的密度函数p(x)=⎪⎩⎪⎨⎧∈ 其它 ,x ,Cx 0[0,1]4,则常数C ＝（ ）A ．51B ．41 C ．4D ．5答案：D11．设随机变量ζ的概率密度为p(x)=⎪⎩⎪⎨⎧<<-其他,0,21a x a a，其中A>0，要使P{ζ>1}=31，则A=（ ） A.1B.2C.3D.4答案：C12．设ζ的分布函数为F(x)=A++∞<<∞-πx x arctan 1，则常数A=（ ）A.21B.1C.2D.π答案：A13. 独立随机变量ξ，η，若ξ～N （1，4），η～N （3，16），下式中不成立．．．的是（ ） A ．E （ξ＋η）＝4B ．E （ξη）＝3C ．D （ξ－η）＝12D ．D （η＋2）＝16答案：C14．将一枚均匀硬币反复抛掷10次，已知前三次抛掷中恰出现了一次正面，则第二次出现正面的概率为（ ）A.31B.21C.41D.103 答案：A15. 13．设随机变量ζ的密度函数p(x)=⎩⎨⎧π∈其他,0],0[x ,ASinx ，则常数A=（ ）A.41B.21 C.1D.2答案：B16.设试验成功概率是p(0<p<1)，则在三次重复独立试验中至少失败一次的概率是( ) A. (1-p)3 B. 1-p 3C. 3(1-p)D. (1-p)3+p(1-p)2+p 2(1-p)答案：B 17.设随机变量X 在[A ，B]上服从均匀分布，则其标准差)(X D 为 A.12/)(2a b -B. 6/)(2a b -C. 32/)(a b -D. 6/)(a b -答案：C18.设),(~2σμN X ，则=)(2X E A.22σμ+B. 2σμ+C.σμ+2D. σμ+答案：A19.若,2)(=X D 则=-)14(X D A.32B.8C. 2D. 31答案：A20.若,2)(,1)(==Y E X E 则=-)2(Y X E A.0B.-1C. 1D. 2答案：A二、多项选择题（略） 三、名词解释1.古典概型2.随机事件的独立性3.分布函数4.依概率收敛[参考答案]1.古典概型：古典概型是指满足下面两个特征的随机试验模型：1）样本空间是有限的，{}n ωωω,,,21 =Ω其中),,2,1(n i i =ω是样本点（基本随机事件）；2）各基本事件的出现是等可能的，即它们发生的概率相同； 3）各基本事件互不相容，即);,,2,1,(j i n j i j i ≠=Φ= ωω2.随机事件的独立性：若事件A 、B 满足)()()(B P A P AB P =，称A 、B 相互独立。

随机事件的独立性与条件概率随机事件的独立性和条件概率是概率论中的重要概念，它们在统计学和实际应用中有着广泛的应用。

了解和理解这些概念对于正确分析和解释随机事件具有重要意义。

首先，我们来看随机事件的独立性。

两个事件A和B被称为独立事件，当且仅当事件A的发生与事件B的发生是相互独立的，即事件A的发生与事件B的发生没有任何关联。

数学上可以用概率的乘法定理来描述独立事件的概率关系。

假设事件A的概率为P(A)，事件B的概率为P(B)，则当且仅当P(A∩B) = P(A) × P(B)时，事件A和B是独立的。

例如，假设我们有一副扑克牌，抽出一张牌的事件A是抽出红心，抽出一张牌的事件B是抽出Q牌。

如果P(A) = 1/4，P(B) = 1/13，而P(A∩B) = 1/52，则事件A 和B是独立的，因为P(A∩B) = P(A) × P(B)。

另外一个重要的概念是条件概率。

条件概率是指在已经发生了某个事件的条件下，另一个事件发生的概率。

条件概率用P(A|B)表示，读作“在事件B已经发生的条件下，事件A发生的概率”。

条件概率可以通过概率的除法定理来计算。

假设事件A和事件B是两个不独立的事件，则P(A|B) = P(A∩B) / P(B)。

以前面的例子为例，已经抽出的牌是红心的条件下，抽出Q牌的概率即为P(B|A) = P(A∩B) / P(A)。

根据前面的数据，我们可以计算得到P(B|A) = (1/52) / (1/4) = 1/13，即在已经抽出红心的条件下，抽出Q牌的概率为1/13。

通过条件概率的概念，我们可以进一步引入贝叶斯公式。

贝叶斯公式是一种计算条件概率的方法，它是由英国数学家贝叶斯提出的。

贝叶斯公式可以用于计算在一些已知条件下，另一个事件发生的概率。

贝叶斯公式可以表示为P(A|B) = P(B|A) × P(A) / P(B)。

贝叶斯公式的应用非常广泛，例如在医疗诊断、信号处理和机器学习等领域中都有重要的应用。