第5章聚类分析.复习过程

第五章聚类剖析5.1鉴别剖析和聚类剖析有何差别？答：即依据必定的鉴别准则，判断一个样本归属于哪一类。

详细而言，设有n 个样本，对每个样本测得p 项指标（变量）的数据，已知每个样本属于k 个类型（或整体）中的某一类，经过找出一个最优的区分，使得不一样类其余样本尽可能地域别开，并鉴别该样本属于哪个整体。

聚类剖析是剖析怎样对样品（或变量）进行量化分类的问题。

在聚类以前，我们其实不知道整体，而是经过一次次的聚类，使邻近的样品（或变量）聚合形成整体。

平常来讲，鉴别剖析是在已知有多少类及是什么类的状况下进行分类，而聚类剖析是在不知道类的状况下进行分类。

5.2试述系统聚类的基本思想。

答：系统聚类的基本思想是：距离邻近的样品（或变量）先聚成类，距离相远的后聚成类，过程向来进行下去，每个样品（或变量）总能聚到适合的类中。

5.3对样品和变量进行聚类剖析时，所结构的统计量分别是什么？简要说明为何这样结构？答：对样品进行聚类剖析时，用距离来测定样品之间的相像程度。

由于我们把n 个样本看作 p 维空间的 n 个点。

点之间的距离即可代表样品间的相像度。

常用的距离为pq)1/ q（一）闵可夫斯基距离： d ij (q) ( X ik X jkk 1q取不一样值，分为（ 1）绝对距离（（ 2）欧氏距离（q 1）q 2 ）（ 3）切比雪夫距离（ q） （二）马氏距离（三）兰氏距离对变量的相像性， 我们更多地要认识变量的变化趋向或变化方向， 所以用有关性进行权衡。

将变量看作 p 维空间的向量，一般用（一）夹角余弦（二）有关系数5.4 在进行系统聚类时，不一样类间距离计算方法有何差别？选择距离公式应按照哪些原则？答： 设 d ij 表示样品 X i 与 X j 之间距离，用 D ij 表示类 G i 与 G j 之间的距离。

（ 1） . 最短距离法（ 2）最长距离法（ 3）中间距离法D kr 21D kp21D kq 2D pq 22 2此中（4）重心法（5）类均匀法（6）可变类均匀法D kr2 (1 )( np D kp2nq D kq2 )D pq2 n r? <1n r此中 ?是可变的且（ 7）可变法D kr21(D kp2 D kq2 )D pq2 此中 ?是可变的且 ? <12（8）离差平方和法往常选择距离公式应注意按照以下的基根源则：（1）要考虑所选择的距离公式在实质应用中有明确的意义。

第五讲聚类分析聚类分析是一种无监督学习方法，旨在将样本数据划分为具有相似特征的若干个簇。

它通过测量样本之间的相似性和距离来确定簇的划分，并试图让同一簇内的样本点相似度较高，而不同簇之间的样本点相似度较低。

聚类分析在数据挖掘、模式识别、生物信息学等领域有着广泛的应用，它可以帮助我们发现隐藏在数据中的模式和规律。

在实际应用中，聚类分析主要包含以下几个步骤：1.选择合适的距离度量方法：距离度量方法是聚类分析的关键，它决定了如何计算样本之间的相似性或距离。

常用的距离度量方法包括欧氏距离、曼哈顿距离、切比雪夫距离等。

2.选择合适的聚类算法：聚类算法的选择要根据具体的问题和数据特点来确定。

常见的聚类算法有K-means算法、层次聚类算法、DBSCAN算法等。

3.初始化聚类中心：对于K-means算法等需要指定聚类中心的方法，需要初始化聚类中心。

初始化可以随机选择样本作为聚类中心，也可以根据领域知识或算法特点选择合适的样本。

4.计算样本之间的相似度或距离：根据选择的距离度量方法，计算样本之间的相似度或距离。

相似度越高或距离越小的样本越有可能属于同一个簇。

5.按照相似度或距离将样本划分为不同的簇：根据计算得到的相似度或距离，将样本划分为不同的簇。

常用的划分方法有硬聚类和软聚类两种。

硬聚类将样本严格地分到不同的簇中，而软聚类允许样本同时属于不同的簇，并给出属于每个簇的概率。

6.更新聚类中心：在K-means等迭代聚类算法中，需要不断迭代更新聚类中心，以找到最优划分。

更新聚类中心的方法有多种，常用的方法是将每个簇内的样本的均值作为新的聚类中心。

7.评估聚类结果：通过评估聚类结果的好坏，可以判断聚类算法的性能。

常用的评估指标有轮廓系数、Dunn指数、DB指数等。

聚类分析的目标是让同一簇内的样本点尽量相似，而不同簇之间的样本点尽量不相似。

因此，聚类分析常常可以帮助我们发现数据中的分组结构，挖掘出数据的内在规律。

聚类分析在市场细分、社交网络分析、基因表达数据分析等领域都有广泛的应用。

例：有一混合样本集，如下图所示，试用ISODATA 进行聚类分析。

解：如下图所示，样本数目8=n ，取类型数目初始值1=c ，执行ISODATA 算法：⑴ 给定参数（可以通过迭代过程修正这些参数）：4,0,4,1,2,2======I L K c s n θθθ预选1x 为聚合中心，即：TZ )0,0(1=。

令1=J ，迭代次数。

⑵ 聚类：因只有一个聚合中心TZ )0,0(1=，故},..,,{:82111x x x X w =，81=n 。

⑶ 因n n θ>=81，没有子集抛弃。

⑷ 计算新聚合中心：∑∈=1811X x x Z T )75.2,38.3()858621,8610821(=++++++++=⑸ 计算类内平均距离：∑∈-=1||||1111X x Z x n D ++++++++=22222222)82()85()86()811()814()819()822()827([8122222222)818()821()810()813()810()85()82()813(+++++++26.2=⑹ 计算类内总平均距离：26.21==D D 。

⑺ 不是最后一次迭代，且2kc =转⑻⑻ 计算聚合1X 中的标准偏差1σ：T ),(12111σσσ=∑∈-=j X x ji J Z x 2111))((81σ])8276()8275()8274()8275()8274()8272()8271()8270[(8122222222-+-+-+-+-+-+-+-=56.1])818()810()810()822()82()86()814()822[(812222222212=+++++++=σ T )56.1,99.1(1=σ⑼ 1σ中的最大偏差分量为99.111=σ，即99.1max 1=σ。

⑽ 因为s θσ>max 1，且2K c =。

所以把聚合分裂成两个子集，5.0=K ，则：T r )0,1(1=，故新的聚合中心分别为：T Z )75.2,38.4(1=+，T Z )75.2,38.2(1=-为方便起见，+1Z 和-1Z 改写为1Z 和2Z ，令1+=c c ，21=+=J J ，返回到⑵。

第一章：多元统计分析研究的容（5点）1、简化数据结构（主成分分析）2、分类与判别（聚类分析、判别分析）3、变量间的相互关系（典型相关分析、多元回归分析）4、多维数据的统计推断5、多元统计分析的理论基础第二三章：二、多维随机变量的数字特征1、随机向量的数字特征随机向量X 均值向量：随机向量X 与Y 的协方差矩阵： 当X=Y 时Cov （X ，Y ）=D （X ）；当Cov （X ，Y ）=0 ，称X ，Y 不相关。

随机向量X 与Y 的相关系数矩阵：2、均值向量协方差矩阵的性质(1).设X ，Y 为随机向量，A ，B 为常数矩阵E （AX ）=AE （X ）；E （AXB ）=AE （X ）B;D(AX)=AD(X)A ’;Cov(AX,BY)=ACov(X,Y)B ’;)',...,,(),,,(2121P p EX EX EX EX μμμ='= )')((),cov(EY Y EX X E Y X --=q p ij r Y X ⨯=)(),(ρ(2).若X ，Y 独立，则Cov(X,Y)＝０，反之不成立．(3).X 的协方差阵D(X)是对称非负定矩阵。

例2.见黑板三、多元正态分布的参数估计2、多元正态分布的性质(1).若 ,则E(X)= ,D(X)= .特别地，当 为对角阵时， 相互独立。

(2).若 ，Ａ为sxp 阶常数矩阵，d 为s 阶向量，ＡＸ＋d ～ . 即正态分布的线性函数仍是正态分布． (3).多元正态分布的边缘分布是正态分布，反之不成立．(4).多元正态分布的不相关与独立等价．例３．见黑板．三、多元正态分布的参数估计(1)“ 为来自p 元总体X 的（简单）样本”的理解---独立同截面． (2)多元分布样本的数字特征---常见多元统计量样本均值向量 ＝样本离差阵Ｓ＝ 样本协方差阵Ｖ＝ S ;样本相关阵Ｒ(3) ,Ｖ分别是 和 的最大似然估计； (4)估计的性质 是 的无偏估计； ,Ｖ分别是 和 的有效和一致估计； ； Ｓ～ ， 与Ｓ相互独立； 第五章 聚类分析：一、什么是聚类分析 ：聚类分析是根据“物以类聚”的道理，对样品或指标进行分类的一种多元统计分析方法。

2．ISODATA聚类算法ISODATA算法：Iterative Self－Organizing Data Analysis Technigues Algorithm，迭代自组织的数据分析算法。

ISODATA算法特点：可以通过类的自动合并（两类合一）与分裂（一类分为二），得到较合理的类型数目c。

具体算法步骤：⑴给定控制参数K：预期的聚类中心数目。

nθ：每一聚类中最少的样本数目，如果少于此数就不能作为一个独立的聚类。

sθ：一个聚类域中样本距离分布的标准差（阈值）。

cθ：两个聚类中心之间的最小距离，如果小于此数，两个聚类合并。

L：每次迭代允许合并的最大聚类对数目。

I：允许的最多迭代次数。

给定n个混合样本，令1=J(迭代次数)，预选c个起始聚合中心，) (J Zj ，cj,...,2,1=。

⑵计算每个样本与聚合中心距离：))(,(JZxDjk。

若：},...,2,1)),(,({min))(,(,...,2,1nkJZxDJZxDjkcjjk===，则：ikwx∈。

把全部样本划分到c个聚合中去，且jn表示各子集j X中的样本数目。

⑶判断：若njnθ<，cj,...,2,1=则舍去子集j X，1-=cc，返回②。

⑷计算修改聚合中心：∑==jnkjkjjxnJZ1)(1)(，cj,...,2,1=。

⑸计算类内距离平均值jD：∑==jn k j j k jj J Z x D n D 1)())(,(1，c j ,...,2,1= ⑹ 计算类内总平均距离（全部样本对其相应聚类中心的总平均距离）：∑=⋅=cj j j D n n D 11 ⑺ 判别分裂、合并及迭代运算等步骤。

（a ）如迭代运算次数已达I 次，即最后一次迭代，置0=c θ，跳到⑾，运算结束。

（b ）如2K c ≤，即聚类中心的数目等于或不到规定值的一半，则转⑻，将已有的聚类分裂。

（c ）如迭代运算的次数是偶数，或K c 2≥，则不进行分裂，跳到⑾，若不符合上述两个条件，则进入⑻，进行分裂处理。

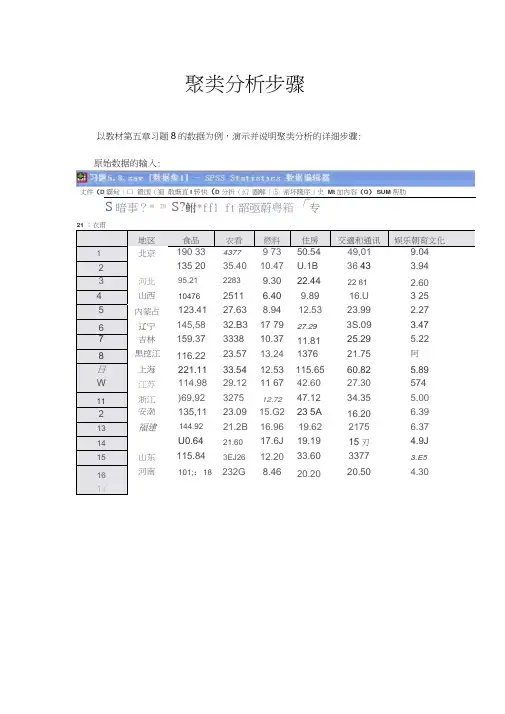
聚类分析步骤以教材第五章习题8的数据为例，演示并说明聚类分析的详细步骤:原始数据的输入:丈件（D 霸甸〔口锻国（蜀散惭直I 转快（D 分折（幻圈解〔⑤ 密坏賤序〔史Mt加内容（Q）SUM 帮肋S暗事？* ™ S?鮒*ffl ft韶亟蔚粤箱「专.选项操作:1. 打开SPSS的“分析”-“分类”-“系统聚类”,打开“系统聚类”对话框。

把“食品”、“衣着”等6变量输入待分析变量框；把“地区”输入“标注个案”；“分群”选中“个案”；“输出”选中“统计量”和“图”。

(如下图)相关说明:(1) 系统聚类法是最常用的方法，其他的方法较少使用。

(2) “标注个案”里输入“地区”，在输出结果的距离方阵和聚类树状图里会显示出“北京”、“天津”等，否则SPSS自动用“ 1”、“2”等代替。

(3) “分群”选中“个案”，也就是对北京等16个样本进行分类，而不是对食品等6个变量分类。

(4) 必须选中“输出”中的“统计量”和“图”。

在该例中会输出16个地区的欧氏距离方阵和聚类树状图。

密Ife鸟駝£臭* I必炮区H-qI 1E曲前 -------------输出v熨计養y岡2. 设置分析的统计量打开最右上角的“统计量”对话框，选中“合并进程表”和“相似性矩阵” “聚类成员”选中“无”。

然后点击“继续”。

打开第二个“绘制”对话框，必须选中“树状图”，其他的默认即可打开第三个对话框“方法”：聚类方法选中“最邻近元素”；“度量标准” 选中“区间”的“欧氏距离”；“转换值”选中“标准化”的“ Z 得分”，并且是“按照变量”。

+区町（LD ： E uclidean 肚屈7" T计徹D ； 卡方度豪▼二鼻細^?TEuclicteeri■|i |g |打开第四个对话框“保存”，“聚类成员”选默认的“无”即可 三•分析结果的解读：按照SPSS 俞出结果的先后顺序逐个介绍：1. 欧氏距离矩阵：是16个地区两两之间欧氏距离大小的方阵， 该方阵是应用各 种聚类方法进行聚类的基础。

第五章 聚类分析5.1 判别分析和聚类分析有何区别？答：即根据一定的判别准则，判定一个样本归属于哪一类。

具体而言，设有n 个样本，对每个样本测得p 项指标（变量）的数据，已知每个样本属于k 个类别（或总体）中的某一类，通过找出一个最优的划分，使得不同类别的样本尽可能地区别开，并判别该样本属于哪个总体。

聚类分析是分析如何对样品（或变量）进行量化分类的问题。

在聚类之前，我们并不知道总体，而是通过一次次的聚类，使相近的样品（或变量）聚合形成总体。

通俗来讲，判别分析是在已知有多少类及是什么类的情况下进行分类，而聚类分析是在不知道类的情况下进行分类。

5.2 试述系统聚类的基本思想。

答：系统聚类的基本思想是：距离相近的样品（或变量）先聚成类，距离相远的后聚成类，过程一直进行下去，每个样品（或变量）总能聚到合适的类中。

5.3 对样品和变量进行聚类分析时， 所构造的统计量分别是什么？简要说明为什么这样构造？答：对样品进行聚类分析时，用距离来测定样品之间的相似程度。

因为我们把n 个样本看作p 维空间的n 个点。

点之间的距离即可代表样品间的相似度。

常用的距离为 （一）闵可夫斯基距离：1/1()()pq qij ik jk k d q X X ==-∑q 取不同值，分为 （1）绝对距离（1q =）1(1)pij ik jk k d X X ==-∑（2）欧氏距离（2q =）21/21(2)()pij ik jk k d X X ==-∑（3）切比雪夫距离（q =∞）1()max ij ik jkk pd X X ≤≤∞=-（二）马氏距离（三）兰氏距离对变量的相似性，我们更多地要了解变量的变化趋势或变化方向，因此用相关性进行衡量。

21()()()ij i j i j d M -'=--X X ΣX X 11()p ik jkij k ik jk X X d L p X X =-=+∑将变量看作p 维空间的向量，一般用（一）夹角余弦（二）相关系数5.4 在进行系统聚类时，不同类间距离计算方法有何区别？选择距离公式应遵循哪些原则？答： 设d ij 表示样品X i 与X j 之间距离，用D ij 表示类G i 与G j 之间的距离。

多元数据分析练习题第二章多元正态的参数估计一. 判断题（1）若∑∑=),,(~),,,(21μp T p N X X X X 是对角矩阵，则p X X X ,,,21 相互独立。

（ ）（2）多元正态分布的任何边缘分布为正态分布，反之也成立。

（ ）（3）对任意的随机向量T p X X X X ),,,(21 =来说，其协方差矩阵∑是对称矩阵，并且总是半正定的。

（ ）（4）对标准化的随机向量来说，它的协方差矩阵与原来变量的相关系数阵相同。

（ ） （5）若),,(~),,,(21∑=μp T p N X X X X S X ,分别为样本均值和样本协差阵，则S nX 1,分别为∑,μ的无偏估计。

（ ） 二.计算题1. 假设随机向量TX X X X ),,(321=的协方差矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=∑9232443416，试求相关系数矩阵R 。

⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=131413112141211R 2. 假设随机向量Tx x x ),(21=的协方差矩阵为⎥⎦⎤⎢⎣⎡=∑20119，令212211,2x x y x x y -=+=，试求T y y y ),(21=的协方差矩阵。

⎥⎦⎤⎢⎣⎡--=∑2733603.假设⎥⎦⎤⎢⎣⎡---=∑5.005.05.015.0),,(~3A N X μ，其中T)1,2,1(-=μ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=∑411121112，试求Ax y =的分布。

)2224,02(2⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-N 三.证明题1.设)()2()1(,,,n X X X 是来自),(∑μp N 的随机样本，X 为样本均值。

试证明：μ=)(X E ，∑=nX D 1)(。

2.设)()2()1(,,,n X X X 是来自),(∑μp N 的随机样本，S n 11-为样本协差阵。

试证明：∑=-)11(S n E 。

3．证明：若p 维正态随机向量),,,(21'=p X X X X 的协差阵为对角矩阵，则X 的各分量是相互独立的随机变量。