应用多元统计分析习题解答-第五章Word版

第二章2.1 试述多元联合分布和边缘分布之间的关系。

设X =(X 1,X 2，⋯X p )′是p 维随机向量，称由它的q （<p ）个分量组成的子向量X(i)=(X i1,X i2，⋯X iq )′的分布为X 的边缘分布，相对地把X 的分布称为联合分布。

当X 的分布函数为F (x 1,x 2，⋯x p )时，X (1)的分布函数即边缘分布函数为F (x 1,x 2，⋯x p )=P(X 1≤x 1,⋯X q ≤x q ,X q+1≤∞,⋯X p ≤∞) = F (x 1,x 2，⋯x q ,∞,⋯∞)当X 有分布密度f （x 1,x 2，⋯x p ）则X (1)也有分布密度，即边缘密度函数为：f （x 1,x 2，⋯x q ）=∫⋯+∞−∞∫f （x 1,x 2，⋯x p ）dx q+1⋯d +∞−∞x p 2.2 设随机向量X =(X 1,X 2)′服从二元正态分布，写出其联合分布密度函数和X 1,X 2各自的边缘密度函数。

联合分布密度函数12πσ1σ2(1−ρ2)1/2exp{−12(1−ρ2)[(x 1−μ1)2σ12−2ρ(x 1−μ1)(x 2−μ2)σ1σ2+f (x 1,x 2)=(x 2−μ2)2σ22]} ， x 1>0,x 2>00 , 其他(x 1−μ1)2σ12−2ρ(x 1−μ1)(x 2−μ2)σ1σ2+(x 2−μ2)2σ22=(x 1−μ1)2σ12−2ρ(x 1−μ1)(x 2−μ2)σ1σ2+(x 2−μ2)2σ22+ρ2(x 1−μ1)2σ12−ρ2(x 1−μ1)2σ12=[ρ(x 1−μ1)σ1−(x 2−μ2)σ2]2+（1−ρ2）(x 1−μ1)2σ12所以指数部分变为−12{[11√1−ρ2σ1−22√1−ρ2σ2]2+(x 1−μ1)2σ12}令t=22√1−ρ2σ2−11√1−ρ2σ1 ∴dt =√1−ρ2σ22∴f (x 1)=∫f (x 1,x 2)+∞−∞dx 2=12πσ1σ2(1−ρ2)1/2exp{−(x 1−μ1)22σ12∫exp(+∞−∞−12t 2√1−ρ22dt =√2πσexp[−(x 1−μ1)22σ12] √2πσexp[−(x 1−μ1)22σ12] ， x 1>0f (x 1)=0 ，其他 同理， √2πσ2exp[−(x 2−μ2)22σ22] ， x 2>0f (x 2)=0 ，其他2.3 已知随机向量X =(X 1,X 2)′的联合分布密度函数为f (x 1,x 2)=2[(d−c )(x 1−a )+(b−a )(x 2−c )−2(x 1−a)(x 2−c)(b−a)2(d−c)2,其中,a ≤x 1≤b,c ≤x 2≤d 。

2.1.试叙述多元联合分布和边际分布之间的关系。

解：多元联合分布讨论多个随机变量联合到一起的概率分布状况，12(,,)p X X X X '=L 的联合分布密度函数是一个p 维的函数，而边际分布讨论是12(,,)p X X X X '=L 的子向量的概率分布，其概率密度函数的维数小于p 。

2.2设二维随机向量12()X X '服从二元正态分布，写出其联合分布。

解：设12()X X '的均值向量为()12μμ'=μ，协方差矩阵为21122212σσσσ⎛⎫ ⎪⎝⎭，则其联合分布密度函数为1/21222112112222122121()exp ()()2f σσσσσσσσ--⎧⎫⎛⎫⎛⎫⎪⎪'=---⎨⎬ ⎪⎪⎝⎭⎝⎭⎪⎪⎩⎭x x μx μ。

2.3已知随机向量12()X X '的联合密度函数为121212222[()()()()2()()](,)()()d c x a b a x c x a x c f x x b a d c --+-----=--其中1ax b ≤≤，2c x d ≤≤。

求（1）随机变量1X 和2X 的边缘密度函数、均值和方差； （2）随机变量1X 和2X 的协方差和相关系数；（3）判断1X 和2X 是否相互独立。

（1）解：随机变量1X 和2X 的边缘密度函数、均值和方差；112121222[()()()()2()()]()()()dx cd c x a b a x c x a x c f x dx b a d c --+-----=--⎰12212222222()()2[()()2()()]()()()()dd c c d c x a x b a x c x a x c dx b a d c b a d c -------=+----⎰ 121222202()()2[()2()]()()()()dd c c d c x a x b a t x a t dt b a d c b a d c ------=+----⎰ 2212122222()()[()2()]1()()()()d cdc d c x a x b a t x a t b a d c b a d c b a------=+=----- 所以 由于1X 服从均匀分布，则均值为2b a+，方差为()212b a -。

5.4经计算可得:<4.64、‘2.8794 10.0100 -1.8091、x = 45.4,S =10.0100 199.7884 -5.64009.965；c 1.8091 -5.6400 3.6277 丿‘0.5862 -0.02210.2580、S'1 = -0.0221 0.0061 -0.0016、0.2580 -0.0016 0.4018 丿S 的特征值和特征向量分别为人=1.3014,q =(—0.8175 0.0249 —0.5754)'& = 4.5316,色=(0.5737 -0.053—0.8173)'入=200.4625心=(0.0508 0.9983 -0.029if由所有(u l9u 2,u 3)组成U 的90%置信椭圆为由于 ^17 (0.1) = 2.44,故有其三个主轴的长度分别为:2列紀 j 如 2xVF^J 鍔X2.44 - 24.8071 2 佝鳩3x19 -—x 2.44 =307.884920x17(b)排汗量XI 的Q ・Q 图:'0.5862 -0.0221 20(4.64一绚,45.4-u 2,9.965一禺)-0.0221 0.0061 ,0.2580 -0.0016 0.2580-0.00160.4018‘4.64 - )45.4 — u 2 W 、9.965 _如丿3x19 1717(0.1)"0.5862 -0.0221 20(4.64 -绚,45.4 一 u 2,9.965 -冷)-0.0221 0.0061、0.2580 -0.0016 0.2580-0.00160.4018孑4.64-普、 45.4 — (9.965-均丿< 8.18123x19 - ------- x 2.44 =46.2911 20x17钠含量X2的Q ・Q 图:QQ Plot of Sample Data X2 versus Standard Normal钾含量的Q-Q 图:70 o o o o6 5 4 3 <D-dlues -ndu- joQQ Plot of Sample Data X1 versus Standard Normal-1.5-0.5 0 0.5 1 Standard Normal Quantiles1.5 29 8 7 6 5 4 3①-dLUBS Indu- jo s ①三UBno-1.5-1-0.5 0 0.5 1 Standard Normal Quantiles1.5 2QQ Plot of Sample Data X3 versus Standard Normal•1.5-105 0 0.5 1 Standard Normal Quantiles1.5 254321098761— 1— XI 和X2的散点图:80 r 70 60 50 40 30 20 XI 和X3的散点图:5 x114—鼻■13*♦12一♦11■ ** *m10■ *♦ ♦98♦ * *« **71 1 1 1 11 ♦2 3 45 678 9X1X2和X3的散点图:14r♦131211co10由排汗量XI 、钠含量X2、钾含量X3数据的Q.Q 都接近于直线，而且各对观察值的散点图 都近似的接近于椭圆，因此可以认为多元正态假定是合理的。

第二章2.1.试叙述多元联合分布和边际分布之间的关系。

解：多元联合分布讨论多个随机变量联合到一起的概率分布状况，12(,,)p X X X X '=的联合分布密度函数是一个p 维的函数，而边际分布讨论是12(,,)p X X X X '=的子向量的概率分布，其概率密度函数的维数小于p 。

2.2设二维随机向量12()X X '服从二元正态分布，写出其联合分布。

解：设12()X X '的均值向量为()12μμ'=μ，协方差矩阵为21122212σσσσ⎛⎫ ⎪⎝⎭，则其联合分布密度函数为1/21222112112222122121()exp ()()2f σσσσσσσσ--⎧⎫⎛⎫⎛⎫⎪⎪'=---⎨⎬ ⎪⎪⎝⎭⎝⎭⎪⎪⎩⎭x x μx μ。

2.3已知随机向量12()X X '的联合密度函数为121212222[()()()()2()()](,)()()d c x a b a x c x a x c f x x b a d c --+-----=--其中1a x b ≤≤，2c x d ≤≤。

求（1）随机变量1X 和2X 的边缘密度函数、均值和方差； （2）随机变量1X 和2X 的协方差和相关系数； （3）判断1X 和2X 是否相互独立。

（1）解：随机变量1X 和2X 的边缘密度函数、均值和方差；112121222[()()()()2()()]()()()dx cd c x a b a x c x a x c f x dx b a d c --+-----=--⎰12212222222()()2[()()2()()]()()()()dd cc d c x a x b a x c x a x c dx b a d c b a d c -------=+----⎰ 12122222()()2[()2()]()()()()dd cc d c x a x b a t x a t dt b a d c b a d c ------=+----⎰2212122222()()[()2()]1()()()()d cdcd c x a x b a t x a t b a d c b a d c b a------=+=----- 所以由于1X 服从均匀分布，则均值为2b a +，方差为()212b a -。

第二章2.1.试叙述多元联合分布和边际分布之间的关系。

解：多元联合分布讨论多个随机变量联合到一起的概率分布状况，12(,,)p X X X X '=的联合分布密度函数是一个p 维的函数，而边际分布讨论是12(,,)p X X X X '=的子向量的概率分布，其概率密度函数的维数小于p 。

2.2设二维随机向量12()X X '服从二元正态分布，写出其联合分布。

解：设12()X X '的均值向量为()12μμ'=μ，协方差矩阵为21122212σσσσ⎛⎫ ⎪⎝⎭，则其联合分布密度函数为1/21222112112222122121()exp ()()2f σσσσσσσσ--⎧⎫⎛⎫⎛⎫⎪⎪'=---⎨⎬ ⎪⎪⎝⎭⎝⎭⎪⎪⎩⎭x x μx μ。

2.3已知随机向量12()X X '的联合密度函数为121212222[()()()()2()()](,)()()d c x a b a x c x a x c f x x b a d c --+-----=--其中1a x b ≤≤，2c x d ≤≤。

求（1）随机变量1X 和2X 的边缘密度函数、均值和方差； （2）随机变量1X 和2X 的协方差和相关系数； （3）判断1X 和2X 是否相互独立。

（1）解：随机变量1X 和2X 的边缘密度函数、均值和方差；112121222[()()()()2()()]()()()dx cd c x a b a x c x a x c f x dx b a d c --+-----=--⎰12212222222()()2[()()2()()]()()()()dd cc d c x a x b a x c x a x c dx b a d c b a d c -------=+----⎰ 12122222()()2[()2()]()()()()dd cc d c x a x b a t x a t dt b a d c b a d c ------=+----⎰2212122222()()[()2()]1()()()()d cdcd c x a x b a t x a t b a d c b a d c b a------=+=----- 所以由于1X 服从均匀分布，则均值为2b a +，方差为()212b a -。

一、填空题：1、多元统计剖析是运用数理统计方法来研究解决多指标问题的理论和方法 .2、回归参数明显性查验是查验解说变量对被解说变量的影响能否著.3、聚类剖析就是剖析怎样对样品（或变量）进行量化分类的问题。

往常聚类分析分为Q型聚类和R型聚类。

4、相应剖析的主要目的是追求列联表行要素A和列要素B的基本剖析特点和它们的最优联立表示。

5、因子剖析把每个原始变量分解为两部分要素：一部分为公共因子，另一部分为特别因子。

6、若x( ): N P( ,),=1,2,3 .n且互相独立，则样本均值向量x 听从的散布为 _ x ~N(μ，Σ /n)_。

二、简答1、简述典型变量与典型有关系数的观点，并说明典型有关剖析的基本思想。

在每组变量中找出变量的线性组合，使得两组的线性组合之间拥有最大的有关系数。

选用和最先精选的这对线性组合不有关的线性组合，使其配对，并选用有关系数最大的一对，这样下去直到两组之间的有关性被提取完成为止。

被选出的线性组合配对称为典型变量，它们的有关系数称为典型有关系数。

2、简述相应剖析的基本思想。

相应剖析，是指对两个定性变量的多种水平进行剖析。

设有两组要素A和B，此中要素 A 包括 r 个水平，要素 B 包括 c 个水平。

对这两组要素作随机抽样检查，获得一个 rc 的二维列联表，记为。

要追求列联表列要素 A 和行要素 B 的基本剖析特点和最优列联表示。

相应剖析即是经过列联表的变换，使得要素 A和要素 B 拥有平等性，进而用同样的因子轴同时描绘两个要素各个水平的情况。

把两个要素的各个水平的情况同时反应到拥有同样坐标轴的因子平面上，进而获得要素 A 、 B 的联系。

3、简述费希尔鉴别法的基本思想。

从 k 个整体中抽取拥有 p 个指标的样品观察数据，借助方差剖析的思想结构一个线性鉴别函数系数：确立的原则是使得整体之间差别最大，而使每个整体内部的离差最小。

将新样 品的 p 个指标值代入线性鉴别函数式中求出 值，而后依据鉴别必定的规则，就能够鉴别新的样品属于哪个整体。

第二章2.1 试述多元联合分布和边缘分布之间的关系。

设，是p维随机向量，称由它的q（<p）个分量组成的子向量，的分布为的边缘分布，相对地把的分布称为联合分布。

当的分布函数为F，时，的分布函数即边缘分布函数为F，=P()= F，当X有分布密度f（，）则也有分布密度，即边缘密度函数为：f（，）=（，）2.2 设随机向量服从二元正态分布，写出其联合分布密度函数和各自的边缘密度函数。

联合分布密度函数，0 , 其他==（）所以指数部分变为令t== exp[] exp[] ，=0 ，其他 同理，exp[] ，=0 ，其他2.3 已知随机向量 的联合分布密度函数为,其中, 。

求：（1） 随机变量各自的边缘密度函数、均值与方差。

解：==同理，==同理可得()22dc x E +=同理可得()()1222d c x D -=（2）随机变量的协方差和相关系数。

E(==E(==E(==E(=D(E(D(E(Cov E(E(=.===（3）判断是否独立。

不相互独立。

2.4设随机向量，服从正态分布，已知其协差阵为对角阵，证明的分量是相互独立的随机变量。

Σ= ΣΣΣΣ与不相关又 ，服从正态分布与 相互独立。

（ ， ， ， ， ， ） 2.5解： 依据题意，X=E(X)=D(X)=注：利用 11p n n ⨯'=1X X , S 1()n n n n''=-11X I X 其中 1001n ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦I 在SPSS 中求样本均值向量的操作步骤如下：1. 选择菜单项Analyze →Descriptive Statistics →Descriptives ，打开Descriptives 对话框。

将待估计的四个变量移入右边的Variables 列表框中，如图2.1。

图2.1 Descriptives 对话框2. 单击Options 按钮，打开Options 子对话框。

在对话框中选择Mean 复选框，即计算样本均值向量，如图2.2所示。

题目：
5.9 对三十个省市自治区根据农林牧副渔各生产值的大小进行分类。

具体分析如下：
对总产值（农林牧渔的加和）进行聚类分析：
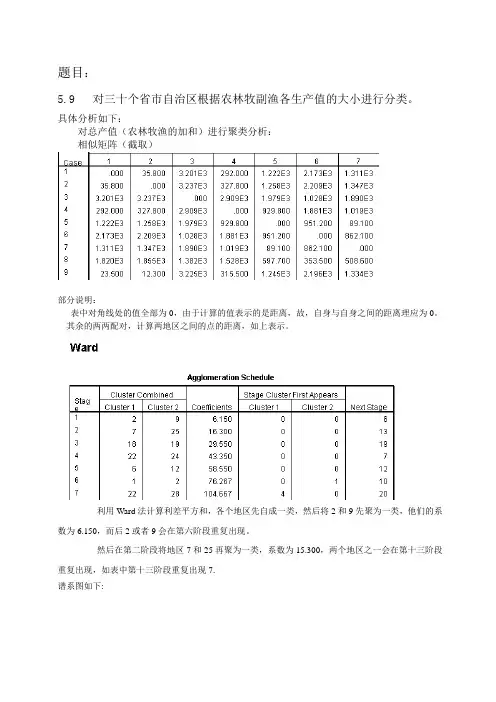
相似矩阵（截取）
部分说明：
表中对角线处的值全部为0，由于计算的值表示的是距离，故，自身与自身之间的距离理应为0。

其余的两两配对，计算两地区之间的点的距离，如上表示。

利用Ward法计算利差平方和，各个地区先自成一类，然后将2和9先聚为一类，他们的系
数为6.150，而后2或者9会在第六阶段重复出现。

然后在第二阶段将地区7和25再聚为一类，系数为15.300，两个地区之一会在第十三阶段
重复出现，如表中第十三阶段重复出现7.
谱系图如下:
可以通过做直线，找与图中线的交点确定所分的类，类所包括的内容以及分类的数目。

较详细接直观的展现。

如下图所示的直线以及分类。

对农业进行聚类：
利用的是皮尔逊相关系数，中位数法，说明不同省市的农业收入是不相关的。

相关系数矩阵（截取）
此处用的是相关系数得到的相似矩阵，故对角线处的元素全部为1。

相同的解释类似于对总产值聚类，故不具体说明。

同时也类似的做出下列谱系图：
从图中可以观察到农业产值在数值之间的差异并不是特别大，同样通过做垂线的办法将其分为
读者预想的类别。

略。

第二章2.1.试叙述多元联合分布和边际分布之间的关系。

解：多元联合分布讨论多个随机变量联合到一起的概率分布状况，12(,,)p X X X X '=的联合分布密度函数是一个p 维的函数，而边际分布讨论是12(,,)p X X X X '=的子向量的概率分布，其概率密度函数的维数小于p 。

2.2设二维随机向量12()X X '服从二元正态分布，写出其联合分布。

解：设12()X X '的均值向量为()12μμ'=μ，协方差矩阵为21122212σσσσ⎛⎫ ⎪⎝⎭，则其联合分布密度函数为1/21222112112222122121()exp ()()2f σσσσσσσσ--⎧⎫⎛⎫⎛⎫⎪⎪'=---⎨⎬ ⎪⎪⎝⎭⎝⎭⎪⎪⎩⎭x x μx μ。

2.3已知随机向量12()X X '的联合密度函数为121212222[()()()()2()()](,)()()d c x a b a x c x a x c f x x b a d c --+-----=--其中1a x b ≤≤，2c x d ≤≤。

求（1）随机变量1X 和2X 的边缘密度函数、均值和方差； （2）随机变量1X 和2X 的协方差和相关系数； （3）判断1X 和2X 是否相互独立。

（1）解：随机变量1X 和2X 的边缘密度函数、均值和方差；112121222[()()()()2()()]()()()dx cd c x a b a x c x a x c f x dx b a d c --+-----=--⎰12212222222()()2[()()2()()]()()()()dd cc d c x a x b a x c x a x c dx b a d c b a d c -------=+----⎰ 12122222()()2[()2()]()()()()dd cc d c x a x b a t x a t dt b a d c b a d c ------=+----⎰2212122222()()[()2()]1()()()()d cdcd c x a x b a t x a t b a d c b a d c b a------=+=----- 所以由于1X 服从均匀分布，则均值为2b a +，方差为()212b a -。

第五章 聚类分析5.1 判别分析和聚类分析有何区别？答：即根据一定的判别准则，判定一个样本归属于哪一类。

具体而言，设有n 个样本，对每个样本测得p 项指标（变量）的数据，已知每个样本属于k 个类别（或总体）中的某一类，通过找出一个最优的划分，使得不同类别的样本尽可能地区别开，并判别该样本属于哪个总体。

聚类分析是分析如何对样品（或变量）进行量化分类的问题。

在聚类之前，我们并不知道总体，而是通过一次次的聚类，使相近的样品（或变量）聚合形成总体。

通俗来讲，判别分析是在已知有多少类及是什么类的情况下进行分类，而聚类分析是在不知道类的情况下进行分类。

5.2 试述系统聚类的基本思想。

答：系统聚类的基本思想是：距离相近的样品（或变量）先聚成类，距离相远的后聚成类，过程一直进行下去，每个样品（或变量）总能聚到合适的类中。

5.3 对样品和变量进行聚类分析时， 所构造的统计量分别是什么？简要说明为什么这样构造？答：对样品进行聚类分析时，用距离来测定样品之间的相似程度。

因为我们把n 个样本看作p 维空间的n 个点。

点之间的距离即可代表样品间的相似度。

常用的距离为 （一）闵可夫斯基距离：1/1()()pq qij ik jk k d q X X ==-∑q 取不同值，分为 （1）绝对距离（1q =）1(1)pij ik jkk d X X ==-∑（2）欧氏距离（2q =）21/21(2)()pi j i k j k k d X X==-∑（3）切比雪夫距离（q =∞）1()max ij ik jkk pd X X ≤≤∞=-（二）马氏距离（三）兰氏距离对变量的相似性，我们更多地要了解变量的变化趋势或变化方向，因此用相关性进行衡量。

21()()()ij i j i j d M -'=--X X ΣX X 11()p ik jkij k ik jk X X d L p X X =-=+∑将变量看作p 维空间的向量，一般用（一）夹角余弦（二）相关系数5.4 在进行系统聚类时，不同类间距离计算方法有何区别？选择距离公式应遵循哪些原则？答： 设d ij 表示样品X i 与X j 之间距离，用D ij 表示类G i 与G j 之间的距离。