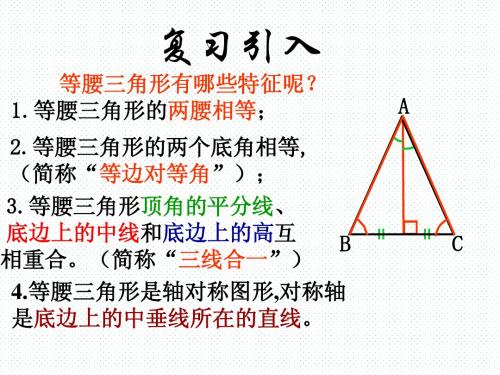
当前位置：文档之家 › 等腰三角形的判定

等腰三角形的判定

  • 格式：ppt
  • 大小：782.00 KB
  • 文档页数：34

下载文档原格式

  / 34

合集下载

等腰三角形的判定

等腰三角形的判定

lpt48hkn
为“藏传佛教的八大神山之首。”我们到达梅里雪山的时候是在早晨，结束了几天的地下生活，到了梅里雪山脚下，阳光刺的我睁不 开眼睛，过了一会终于适应了。阳光明媚，山上的雪被阳光照得熠熠生辉，极蓝与极白相交辉映，看着这样的风景好像心也被洗干净 了，空气里都满是雪的味道。我现在终于体会到什么是壮观，在大自然的面前人类是多么的渺小。巍峨的雪山直插云霄，真是雾笼云 遮缥缈中，浑然浩气贯苍穹。山神说拉着我的手，我啊了一声，有点不好意思，脸红的发烫，感觉都红到耳根了。山神看着我说： “想什么呢，拉着我，我们飞上去，这样会节省不少时间。”这是要是有一条地缝，不管多小，我都要挤进去。可等了半天，山神也 没什么动静，他的手依旧如此冰凉。我以为他还在酝酿，只见他眉头紧皱，我说怎么了，我们怎么还在这里。山神说：“在这里，我 居然不能使用法术，我的法术好像被什么禁锢了一样，没法使出来。”我心想这座山这么厉害，居然连山神的法力都被禁锢了，看来， 我们凶多吉少了，真是壮士一去兮不复返啊。我说：“这样啊，那我们还是走吧，万一在这里挂掉了，我还好，你可怎么办啊，多不 划算啊。”我边说边往回走。山神说：“来都来了，再说了，怕什么，这是神山，不会有什么妖怪的。看来，我们只有爬上去了”。 这里有十三座峰，主峰卡瓦格博峰海拔高达6740米，看着主峰，我咽了口唾沫，心想这次不死也要退层皮了。我们修整了一会开始爬 山，我们就一直走，也无心欣赏身边的风景了，山很陡峭，有几次险些摔倒下去，我们一直提心吊胆地走了一天，到傍晚的时候终于 到达了雪线，我们又继续往前走，天也渐渐暗下来了，想想开始露出来，星星离我们很近，温度逐渐降低，风越来越大，尽管穿着很 厚很厚地冬衣，依然感觉很冷，只要一张口，风吹着雪就直往喉咙里灌，山神怕我摔倒后爬不起来，就一直拉着我走，满眼的白色， 一直看着白色突然头一阵眩晕，一不小心就跌了个狗**。山神连忙把我扶起来。山神还是一身玄色衣服，他无论在什么样的恶劣条件 都是这样，丝毫不受影响。走到后来就是他拖着我走了，他怕我失去意识，就一直不停的跟我说话。我们又走了一夜，到第二天中午， 我们来到了一个山洼里，这的山洼很奇怪，它很宽很大，周围长满了野花和野草，还能看到很多蝴蝶，一条清澈的小溪从旁边流过， 这里这的是一处世外桃源啊，想不到大山之中还能有这样的地方不受风雪的侵扰。山神的眼睛很尖，一下就看到了被草掩埋的相机， 拿起来一看，这是尼康FM3A上面的金属机身已经长锈了，相机更新速度很快，现在已经停产了，我们也不能评这个就判断时间，万一 他是胶卷相机的忠实用户呢，这也说不定，随后我们又找到

等腰三角形的判定

等腰三角形的判定

等腰三角形的判定一．知识点：等腰三角形的判定方法 ①定义：有 的三角形叫做等腰三角形。

②定理：如果一个三角形有 ,那么这两个角所对的边也相等. 简写成“ ”.二．典例分析：例1：如图：（1）已知：OD 平分∠AOB ，ED ∥OB ，求证：EO=ED 。

（2）已知：OD 平分∠AOB ，EO=ED 。

求证：ED ∥OB 。

（3）已知：ED ∥OB ，EO=ED 。

求证：OD 平分∠AOB 。

例2：（1）已知：如图a ，AB=AC ，BD 平分 ∠ABC ，CD 平分∠ACB ，过D 作EF ∥BC 交AB 于E,交AC 于F,则图中有几个等腰三角形?（2）如图b,AB=AC,BF 平分∠ABC 交AC 于F ，CE 平分∠ACB 交AB 于E ，BF 和BE 交于点D ，且EF ∥BC ，则图中有几个等腰三角形?（3）等腰三角形ABC 中，AB=AC ，BD 平分∠ABC ，CD 平分∠ACB ，过A 作EF ∥BC 交CD 延长线于E,交BD 延长线于F,则图中有几个等腰三角形?（自己画图）（4）如图c,若将第(1)题中的AB=AC 去掉,其他条件不变,情况会如何?还可证出哪些线段的和差关系?EDCAB （5）如图,若BD,CD 分别平分∠ABC 和∠ACB,过D 作DE ∥AB 交BC 于E,作DF ∥AC 交BC 于F.求证:BC 的长等于△DEF 的周长.推广① 当过△ABC 的一个内角和一个外角平分线的交点作这两角的公共边的平行线时：(6)如图，已知CE 、CF 分别平分∠ACB 和它的外角，EF∥BC，EF 交AC 于D 。

求证：DE=DF 。

(7)已知BD 、CD 分别平分∠A BC 和∠ACB 的外角，EF∥BC，BD 、CD 与EF 交于D 。

求证： EF ＝ BE －CF ．AE F D B C推广②当过△ABC 的两个外角平分线上一点作这两个角的公共边的平行线时：(8)已知AD 、CD 分别平分∠ACB 的外角和∠ACB 的外角，EF∥AC ，AD 、CD 与EF 交于D 。

等腰三角形的判定

等腰三角形的判定
O
A
B
O 已知：如图，在ΔOAB中， ∠A=∠B，求证:OA=OB. A C 证明：过O点作OC⊥AB，垂足为C. 在ΔOAC和ΔOBC中， ∠A=∠B ∠OCA= ∠OCB=90° OC=OC ∴ ΔOAC ≌ΔOBC ∴ OA=OB
B
等腰三角形的判定：
如果一个三角形中有两个角 相等,那么这两个角所对的边也相 等.(等角对等边)
A 有两边 相等的 三角形 是等腰 三角形。 C
1.两边相等。
2.等边对等角, 3. 三线合一。 4.是轴对称图形.
2.等角对等边,
思考题1 如图,线段AB的端点B在直线 l 上(AB与直线 l 不 垂直)，请在直线 l 上另找一点C,使ΔABC为等腰 三角形，这样的点能找几个？你能说出它们的画 法吗？ A
理由．
B
30
O
60
O
A D
C
心动
不如行动
A
如图:△ABC中AB=AC,∠B=∠C， BD=CE，说明∠1=∠2的理由，
B D
1
2
E ∠1=∠2
C
方法一:
BD=CE ∠B=∠C AB=AC
△ABD≌ △ACE
AD=AE
方法二: △ABD≌ △ACE
方法三:
BE=CD ∠B=∠C AB=AC
∠ADB＝∠AEC
A C
如图，标杆AB高5m， 为了将它固定，需要由 它的中点C向地面上与点 B距离相等的D，E两点 拉两条绳子，使得点D， B，E在一条直线上。量 得DE=4m，绳子CD和 CE要多长？
E
D
B
例1：一次数学实践活动的内容是测量河宽，如图，即 测量A,B之间的距离.同学们想出了许多方法,其中小聪 的方法是：从点Ａ出发,沿着与直线AB成60°角的AC方 向前进至C，在C处测得∠C＝30°.量出AC的长，它就是 河宽（即A,B之间的距离）．这个方法正确吗？请说明

等腰三角形的判定

等腰三角形的判定

等腰三角形的判定
首先，我们来看一下如何判定一个三角形是否为等腰三角形。

一个三角形是等
腰三角形的条件是它的两条边相等。

这意味着三角形的两条边的长度必须相等，而第三条边可以与它们不相等。

当我们知道一个三角形的三条边的长度时，我们可以通过比较这些长度来判断它是否为等腰三角形。

另外，等腰三角形还具有一些独特的性质。

首先，等腰三角形的两个底角（即
两条边对应的角）是相等的。

这意味着如果我们知道一个等腰三角形的两个底角的大小，我们就可以确定它是等腰三角形。

其次，等腰三角形的高（即从顶点到底边的垂直距离）是对称轴，这意味着等腰三角形的高将底边分成两个相等的部分。

最后，等腰三角形的顶角（即顶点对应的角）是小于180度的锐角。

等腰三角形在几何学中有着广泛的应用。

首先，等腰三角形是其他类型三角形
的特例，因此我们可以通过研究等腰三角形来理解更一般的三角形性质。

其次，等腰三角形的性质可以应用于解决各种几何问题，例如计算三角形的面积、判断一个三角形是否为等边三角形等等。

另外，等腰三角形还经常出现在建筑和工程中，例如等腰三角形的结构可以用于设计桥梁、建筑物和其他结构。

总之，等腰三角形是一种常见的三角形，它具有独特的性质和特征。

通过研究
等腰三角形，我们可以更好地理解三角形的性质和几何学的基本原理。

同时，等腰三角形的应用也广泛存在于各个领域，包括数学、建筑和工程等。

希望本文对读者对等腰三角形有所帮助，也希望读者能够进一步深入研究和应用等腰三角形的知识。

等腰三角形判定

等腰三角形判定

⑶过点A作y轴的垂线交y轴于E，F为x轴负半轴上一点，
G在EF的延长线上，以EG为直角边作等腰Rt△EGH， 过A作x轴垂线交EH于点M，连FM，等式 是否成立？若成立，请证明：
已知:如图,DE∥BC,∠1=∠2.
求证:BD=CE.
证明: ∵∠1=∠2（已知）
∴AD=AE（等角对等边） ∵DE∥BC（已知） ∴∠1=∠B，∠2=∠C ∴∠B=∠C ∴AB=AC（等角对等边） ∴AB－AD=AE－AC B D 1
A
2 E
C
即 BD=CE
例3、如图，把一张矩形的纸沿对角线折叠，重合 的部分是一个等腰三角形吗？为什么？ 2 解：重合部分是等腰三角形。 理由：由ABDC是矩形知 AD∥BC A ∴∠ 3= ∠ 2 由沿对角线折叠知 1 ∠1=∠3 B 3 ∴ ∠ 1= ∠ 2 ∴ BF=DF（等角对等边）
3、注意：该方法不能直接使用，只能提供一种证等腰 的基本思想，要运用必须予以证明。
1、已知:如图,AD交BC于点O, AB∥CD,OA=OB. 求证:OC=OD
证明:
∵OA=OB(已知) ∴∠A=∠B(等边对等角）
∵AB∥CD(已知) C
A O
B
D
∴∠C= A=∠D. D,∠B=∠C(两直线平行,内错 角相等) ∴OC=OD(等角对等边）
C 110° 20° 50°
A
B
比较本题和练习册P37 7的不同之处。
1、对∠A进行讨论
2、对∠B进行讨论
3、对∠C进行讨论
C
20° 20°
C
65° 65° 50° 35°
C
110° 35°
A C
20° 20°
BA C
50°

等腰三角形的判定和性质

等腰三角形的判定和性质
2 等腰三角形 第1课时 等腰三角形的判定和性质
一、等腰三角形的性质 1.定理:等腰三角形的两个底角相等.简述为: 等边对等角 . 2.定理:等腰三角形顶角的平分线、底边上的 中线 、底边上的 高
互相
重合.这一结论通常简述为“三线合一”. 3.等腰三角形两底角的平分线 相等 ;两条腰上的中线 相等 的高 相等 .
;两条腰上
【知识拓展】 等腰三角形底边上任意一点到两腰的距离和等于一腰上的高. 二、等腰三角形的判定
有两个角相等的三角形是等腰三角形.简述为: 等角对等边 .
知识点一 等腰三角形的性质
【例1】如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E. 求证:∠CBE= ∠BAD.
证 明 : 法 一 因 为 AB=AC,AD 是 BC 边 上 的 中 线 , 所 以 AD⊥BC,∠BAD=∠CAD, 所 以 ∠ CAD+ ∠C=90°. 因 为 BE⊥AC, 所 以 ∠ CBE+∠C=90°. 所 以 ∠ CBE=∠CAD, 所 以 ∠CBE=∠BAD. 法二 因为AB=AC,所以∠ABC=∠C.又因为AD是BC边上的中线,所以AD⊥BC,所以 ∠BAD+ ∠ABC=90°.因为BE⊥AC,所以∠CBE+∠C=90°,所以∠CBE=∠BAD.
解:(1)①②;①③.
(2)请选择(1)中的一种情形,写出证明过程.
解:(2)选①②证明如下:在△BOE和△COD中, 因为∠EBO=∠DCO,∠EOB=∠DOC,BE=CD, 所以△BOE≌△COD,所以BO=CO, 所以∠OBC=∠OCB, 所以∠EBO+∠OBC=∠DCO+∠OCB, 即∠ABC=∠ACB,所以AB=AC, 即△ABC是等腰三角形. 选①③证明如下: 在△BOC中,因为OB=OC,所以∠OBC=∠OCB. 因为∠EBO=∠DCO, 所以∠EBO+∠OBC=∠DCO+∠OCB, 即∠ABC=∠ACB,所以AB=AC,即△ABC是等腰三角形.

等腰三角形的判定

即△ABC是等腰三角形。
结论： 如果三角形一个外角的平分线 平行于三角形的一边，那么这个三 角形是等腰三角形。
巩固练习三
1.已知:如图,AD∥BC,BD平分∠ABC,试判断 △ABD的形状,并说明理由? 答:△ABD是等腰三角形. A D 3 理由: ∵BD平分∠ABC ∴∠1=∠2 (角平分线定义) 1 2 ∵AD∥BC B C ∴∠2=∠3 (两直线平行,内错角相等) ∴∠1=∠3 ∴AB=AD (等角对等边) 即△ABD是等腰三角形.
开启
智慧
思考1:如图,在△ABC中，已知∠ABC=∠ACB， BF平分∠ABC，CF平分∠ACB,请想想看,由以上 条件,你能推导出什么结论?并说明理由.
如ቤተ መጻሕፍቲ ባይዱEG∥BC？ A
E
F
G
B
C
开启 思考 2:
智慧
下例各说法对吗？为什么？
等腰三角形两底角的平分线相等. 等腰三角形两腰上的中线相等. 等腰三角形两腰上的高相等.
巩固练习三
2.如图，在等腰△ABC中，AB=AC，两 A 底角的平分线BE和CD相交于点O，那么 △OBC是什么三角形？为什么？ 答：△OBC是等腰三角形。 D O E 理由：∵△ABC中，AB=AC ∴∠ABC=∠ACB（等边对等角） 1 2 C ∵BE平分∠ABC，CD平分∠ACB B 1 1 ∴∠1= ∠ABC，∠2= ∠ACB， （角平分线定义） 2 2 ∴∠1=∠2 ∴OB=OC （等角对等边） 即△OBC是等腰三角形。
小 结
名称 图 等
腰 三 角 形 B D
形
概 念 性质与边角关系
识
别
A
1.如果AB=AC, 1.两腰相等， 则△ABC是等腰 即AB=AC 有两边 三角形。 相等的 三角形 2.等边对等角,即 2.等角对等边, 即∵ ∠B=∠C 是等腰 ∵AB=AC, ∴ AB=AC。 三角形。 ∴∠B=∠C。 C 3.顶角的平分线、 底边上的中线和高 三线合一。 4.是轴对称图形.

等腰三角形的判定


课堂作业： 课堂作业： 课本P99： ： 课本 第1，2，3，4 ， ， ， 题
敬 请 各 位 老 师 指 导
再见
D
等腰三角形的判定方法： 等腰三角形的判定方法：
如果一个三角形有两个角相等， 如果一个三角形有两个角相等，那 么这两个角所对的边也相等， 么这两个角所对的边也相等，即这个三角 形是等腰三角形。简单地说， 形是等腰三角形。简单地说， 在同一个三角形中，等角对等边。 在同一个三角形中，等角对等边。 A 用数学语言叙述此判定: 用数学语言叙述此判定 在△ABC中， 中 ∵∠B=∠ ∵∠ ∠C ∴AB=AC(在一个三角形 在一个三角形 B C 中,等角对等边 等角对等边) 等角对等边
欢迎你走进今天的 数学 课堂！
我们在上一节学习了 等腰三角形的性质。 等腰三角形的性质。 现在你能回答我一些 问题吗？ 问题吗？
复习引入
等腰三角形有哪些特征呢？ 等腰三角形有哪些特征呢？ 1.等腰三角形的两腰相等； 等腰三角形的两腰相等 1.等腰三角形的两腰相等； 2.等腰三角形的两个底角相等, 2.等腰三角形的两个底角相等, 等腰三角形的两个底角相等 简称“等边对等角” （简称“等边对等角”）； 3.等腰三角形顶角的平分线 等腰三角形顶角的平分线、 3.等腰三角形顶角的平分线、 底边上的中线和底边上的高互 B 相重合。（简称“三线合一”） 相重合。（简称“三线合一” 。（简称 4.等腰三角形是轴对称图形 对称轴 等腰三角形是轴对称图形,对称轴 等腰三角形是轴对称图形 是底边的中垂线。 是底边的中垂线。 A
A
解： ⊿ABC中 中 ∵AB=AC， ， 等边对等角） ∴ ∠B=∠C （等边对等角） ∠ ∵ ∠ A=600 ∴ ∠B=∠C = 600 ∠ ∴AB=AC=BC

等腰三角形判定定理的证明

等腰三角形判定定理的证明
要证明一个三角形是等腰三角形，需要证明其两条边相等。

设三角形的三条边分别为a、b、c，且为等腰三角形。

不失一般性，假设a=b，则有以下两种情况：
1. 如果a=b=c，则三角形是等边三角形，也是等腰三角形。

2. 如果a=b≠c，则根据等腰三角形的定义，只需要证明c是a 和b的中线即可。

我们可以通过使用三角形的余弦定理来证明这一点。

根据三角形的余弦定理，可以得到以下等式：
c^2 = a^2 + b^2 - 2ab * cos⁡(∠C)
由于a=b，所以a^2 = b^2，上述等式可以简化为：
c^2 = 2a^2 - 2a^2 * cos⁡(∠C)
因为∠C是锐角或直角，所以cos⁡(∠C) < 1，因此2a^2 * cos⁡(∠C) < 2a^2。

因此，c^2 < 2a^2，或者说c < √2 * a。

因此，在这种情况下，c < √2 * a，证明了c是a和b的中线。

因此，三角形是等腰三角形。

综上所述，根据等腰三角形的定义和余弦定理的推导，我们可以得出等腰三角形判定定理的证明。

等腰三角形的判定课件(共21张PPT)

复习回顾
等腰三角形的性质定理
1、从边看：等腰三角形的两腰相等。 （定义）
2、从角看：等腰三角形的两底角相等。 （性质定理1）
3、从重要线段看：等腰三角形的顶角平分线、 底边上的中线和底边上的高三线合一。 （性质定理2）
如何判定一个三角形是等腰三角形？
定义：有两边相等的三角形是等腰三角形。
还有其他方法吗？
A
B
D C
例2：已知：AD交BC于点O，AB∥CD，OA=OB
求证：OC=OD
问题：
1、若已知AB∥ CD，OC=OD，能
A
否证明OA=OB？
2、若已知OA=OB，OC=OD，能否
证明AB ∥ CD？
C
B O
D
规律：
AB ∥ CD，OA=OB，OC=OD中已知任两 个可推出第三个。
例3、如图，在Rt△ABC和Rt△A’B’C’中,
已知：△ABC中，∠B=∠CBAC的平分线AD
A
在△ BAD和△ CAD中， 1 2
∠B=∠C，
∠1=∠2，
B
AD=AD
C
D
∴ △ BAD≌ △ CAD（AAS）
∴AB=AC（全等三角形的对应边相等）
思考:作底边上的高可以吗?作底边中线呢?
等腰三角形的判定定理：
如果一个三角形有两个角相等,那么这两个 角所对的边也相等(简写成“等角对等边”)
∠ABC= ∠A’B’C’=90°，
AB=A’B’,AC=A’C’，
区别:条件和结论互换。
3、已知：ED ∥ OB，EO=ED
求证：Rt△ABC≌Rt△A’B’C’ 求证：OD平分 AOB。
例1 :已知：如图，∠CAE是△ABC的外角∠1=∠2，
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

从B处到灯塔C的解距：离∵ ∠NAC=40°∠NBC=80°
∴∠C=∠NBC-∠NAC
C
80° N 北
=80°-40° = 40°
B
∴ ∠C = ∠A
40°
∴ BA=BC（等角对等边）
A
里）∵AB=20×（12-10）=40（海 ∴BC=40 （海里）
答：B处到达灯塔C的距离为40海里。
.
在△ABC中，AB=AC，∠ABC和∠ACB的平分线交
若AB≠AC，其他 条件不变，图中 还有等腰三角形
∵ EF=EO+FO
吗？(1)中结论还
∴EF＝BE+FC
成立吗？
.
求证：如果三角形一个外角的平分线平行于三 角形的一边，那么这个三角形是等腰三角形。
E
1
A2
已知：如图，∠CAE是△ABC D 的外角， ∠1=∠2，AD∥BC
求证：AB=AC
B
C
分析：要证AB=AC，就要证∠B=∠C，而已知 有∠1= ∠2，只要找出∠B、 ∠C与∠1、 ∠2的 关系就可以了。
∵ BD平分∠ABC B
C
∴ ∠ABD=∠DBC
∴ ∠ABD=∠ADB(等量代换)
∴ AB=AD(等角对等边)
∴AB=AC (等角对等边)
.
已知：在△ABC 中，∠1=∠3,∠2=∠4，AD
平分∠BAC。求证：AD⊥BC
A
证明： ∵ ∠1=∠3,∠2=∠4
∴ ∠1+∠2=∠3+∠4
即 ∠ABC=∠ACB
不考虑风浪因素）？
O
A
B
.
探 究 新 知
做一做
● 操作一 画△ABC.使∠B＝∠C＝30°
● 操作二 量一量，线段AB与AC的长度。
你发现了什么结论？其他同学的结果与你
的相同吗？
怎样用数
学推理进
AB=AC
行证明呢？
.
如果一个三角形有两个角相等,那么这两 个角所对的边也相等
已知：如图,在ΔABC中，∠B=∠C。
D
∴AB=AC (等角对等边)
1
3
∵ AD平分∠BAC
2
4
∴ ∠BAD=∠CAD
B
C
∴ AD在等腰△ABC 的顶角的角平分线上
∴ AD⊥BC (等腰三角形的“三线合一”)
小试牛刀
例：如图,上午10 时，一条船从A处出发以20海里
每小时的速度向正北航行，中午12时到达B处，从
A、B望灯塔C，测得∠NAC=40°∠NBC=80°求
A
求证：AB=AC
证明: 作∠BAC的平分线AD
∴∠1=∠2 在△BAD和△CAD中
∠B=∠C(已知)
∵ ∠1=∠2(已证)
AD=AD (公共边) ∴ △BAD ≌ △CAD (A.A.S.)
12
B
DC
你还有其 他证法吗
∴ AB= AC (全等三角形的对应边相等)
?
.
已知：如图,在ΔABC中，∠B=∠C。
求证：AB=AC
A
证明：作AD⊥BC，垂足为D
∴ ∠ADB= ∠ADC=900
在 △BAD和△CAD中，
□
∵
∠B=∠C(已知) ∠ADB= ∠ADC(已证)
B
□ D
AD=AD(公共边） C ∴ △BAD≌△CAD（A.A.S.）
∴AB=AC（全等三角形的对应边
相等）
.
注意：在同一个 等腰三角形的判定定理： 三角形中应用哟！
A
B
.
已知：在等腰△ABC中，AB=AC， ∠A=60°(或者∠B=60°）
求证：AB=AC=BC A
60°
60°
B
C
你又可以得到什么？
.
推论2：有一个角等于60°的等腰三 角形是等边三角形。
这是由判定定理推导出的又一个定理， 即判定一个三角形是等边三角形的另 外一种方法。
.
等边三角形的判定定理2： 有一个角为60°的等腰三角形是等边三角形．
A
证明： ∵ DE∥BC ∴ ∠1=∠B,∠2=∠C ∵ ∠1=∠2 ∴AD=AE(等角对等边) ∠B=∠C(等量代换)
∴AB=AC (等角对等边) ∴AB-AD=AC-AE
即 BD=CE
D1 2 E
B
C
.
已知：如图，AD∥BC，BD平分∠ABC
求证：AB=AD
A
D
证明： ∵ AD∥BC
∴ ∠ADB=∠DBC
一、复习引入 等腰三角形 定义： 有两边相等的三角形是等腰三角形。 性质1： 等腰三角形的两个底角相等。
(等边对等角)
性质2： 等腰三角形的底边上的中线和高线、 顶角平分线互相重合。 (三线合一)
.
问题情境 ：
如图，位于海上A、B两处的两艘救生船接到O处 遇险船只的报警，当时测得∠A=∠B。如果这两艘救生 船以同样的速度同时出发，能不能同时赶到出事地点（
如果一个三角形有两个角相等，那么 这两个角所对的边也相等
(简写成“等角对等边”)。
A
几何语言：
∵∠B =∠C (已知)
∴ AB=AC(等角对等边) B
C
.
等腰三角形的性质与判定有区别吗? 性质是:1.等边 等角 2.三线合一 判定是:等角 等边
.
已知:如图,DE∥BC,∠1=∠2.求证:BD=CE.
.
已知：如图，∠CAE是△ABC的外角， ∠1=∠2， AD∥BC。求证：AB=AC
解：∵AD∥BC
E
1
A2
∴∠1= ∠B (两直线平行，同位角相等） D ∠ 2 ＝ ∠C(两直线平行，内错角相等）
∵ ∠1= ∠2
B
C
∴ ∠B ＝ ∠C(等量代换)
∴AB=AC (等角对等边）
.
已知：在△ABC中，∠A=∠B=∠C 求证：AB=AC=BC A
B
C
从以上讲解我们可以得到什么结论？
.
推论1：三个角都相等的三角形是等边三角形 。
这是由判定定理推导出的一个定理， 即判定一个三角形是等边三角形的一 种方法。
.
细心观察，探索性质
等边三角形的判定定理1：
三个角都相等的三角形是等边三角形．
符号语言：
C
在△ABC 中，
∵ ∠A=∠B =∠C ，
∴ △ABC 是等边三角形．
于点O.过O作EF∥BC交AB于E，交AC于F.请你写出
图中所有等腰三角形，并探究EF、BE、FC之间的关
系
AA
解：EF=BE+CF 理由如下：
∵ BO、CO分别平分∠ABC、∠ACB ∴∠2＝∠ABO ，∠3＝∠ACO ∵ EF∥BC ∴∠1＝∠2 ，∠3＝∠4
E E
B B
O FF
1 4C
2
3C
∴∠1＝∠ABO ∠4＝∠ACO ∴BE＝EO FC=FO (等角对等边)
C
符号语言：
在△ABC 中，
∵ BC =AC，∠A =60°
∴ △ABC 是等边三角形． A
B
.
△ABC 是等边三角形，DE∥BC, 分别交AB， AC 于点D，E．求证：△ADE 是等边三角形.
A
证明：∵ △ABC 是等边三角形，
∴ ∠A =∠B =∠C =60°．
∵ DE∥BC，
D

∴ ∠ADE =∠B =60° ， B