抛物线焦点弦的弦长公式

微重点 抛物线的二级结论的应用抛物线是高中数学的重要内容之一，知识的综合性较强，因而解题时需要运用多种基础知识，采用多种数学手段，熟记各种定义、基本公式．法则固然很重要，但要做到迅速、准确地解题，还要掌握一些常用结论，特别是抛物线的焦点弦的一些二级结论，在考试中经常用到，正确灵活地运用这些结论，一些复杂的问题便能迎刃而解．考点一 抛物线的焦点弦核心提炼与抛物线的焦点弦有关的二级结论若倾斜角为α⎝⎛⎭⎫α≠π2的直线l 经过抛物线y 2＝2px (p >0)的焦点，且与抛物线相交于A (x 1，y 1)，B (x 2，y 2)(y 1>y 2)两点，则(1)焦半径|AF |＝x 1＋p 2＝p1－cos α，|BF |＝x 2＋p 2＝p1＋cos α，(2)焦点弦长|AB |＝x 1＋x 2＋p ＝2psin 2α，(3)S △OAB ＝p 22sin α(O 为坐标原点)，(4)x 1x 2＝p 24，y 1y 2＝－p 2，(5)1|AF |＋1|BF |＝2p， (6)以AB 为直径的圆与准线相切，以F A 为直径的圆与y 轴相切．考向1 焦半径、弦长问题例1 (1)已知F 是抛物线C ：y 2＝4x 的焦点，过点F 作两条相互垂直的直线l 1，l 2，直线l 1与C 相交于A ，B 两点，直线l 2与C 相交于D ，E 两点，则|AB |＋|DE |的最小值为( ) A ．16 B ．14 C ．12 D ．10 答案 A解析 如图，设直线l 1的倾斜角为θ，θ∈⎝⎛⎭⎫0，π2，则直线l 2的倾斜角为π2＋θ，由抛物线的焦点弦弦长公式知|AB |＝2p sin 2θ＝4sin 2θ， |DE |＝2p sin 2⎝⎛⎭⎫π2＋θ＝4cos 2θ，∴|AB |＋|DE |＝4sin 2θ＋4cos 2θ＝4sin 2θcos 2θ＝16sin 22θ≥16，当且仅当sin 2θ＝1， 即θ＝π4时取等号．∴|AB |＋|DE |的最小值为16.(2)斜率为3的直线经过抛物线y 2＝2px (p >0)的焦点F 与抛物线交于A ，B 两点，A 在第一象限且|AF |＝4，则|AB |＝________. 答案163解析 直线l 的倾斜角α＝60°，由|AF |＝p1－cos α＝4，得p ＝4(1－cos α)＝2， ∴|AB |＝2p sin 2α＝434＝163. 考向2 面积问题例2 (2022·长沙模拟)已知抛物线C ：y 2＝16x ，倾斜角为π6的直线l 过焦点F 交抛物线于A ，B 两点，O 为坐标原点，则△ABO 的面积为________． 答案 64解析 方法一 (常规解法)依题意， 抛物线C ：y 2＝16x 的焦点为F (4,0)，直线l 的方程为x ＝3y ＋4.由⎩⎨⎧x ＝3y ＋4，y 2＝16x ，消去x ， 得y 2－163y －64＝0. 设A (x 1，y 1)，B (x 2，y 2)， 则y 1＋y 2＝163，y 1y 2＝－64. S △OAB ＝12|y 1－y 2|·|OF |＝2(y 1＋y 2)2－4y 1y 2＝2(163)2－4×(－64)＝64. 方法二 (活用结论)依题意知， 抛物线y 2＝16x ，p ＝8. 又l 的倾斜角α＝π6.所以S △OAB ＝p 22sin α＝822sinπ6＝64.考向31|AF |＋1|BF |＝2p的应用 例3 (2022·“四省八校”联考)已知抛物线y 2＝4x ，过焦点F 的直线与抛物线交于A ，B 两点，则2|AF |＋|BF |最小值为( ) A ．2 B ．26＋3 C ．4 D ．3＋2 2答案 D解析 因为p ＝2， 所以1|AF |＋1|BF |＝2p ＝1，所以2|AF |＋|BF |＝(2|AF |＋|BF |)·⎝⎛⎭⎫1|AF |＋1|BF | ＝3＋2|AF ||BF |＋|BF ||AF |≥3＋22|AF ||BF |·|BF ||AF |＝3＋22， 当且仅当|BF |＝2|AF |时，等号成立， 因此，2|AF |＋|BF |的最小值为3＋2 2.考向4 利用平面几何知识例4 (2022·遂宁模拟)已知F 是抛物线C ：y 2＝2px (p >0)的焦点，过点F 的直线l 与抛物线交于P ，Q 两点，直线l 与抛物线的准线l 1交于点M ，若PM →＝2FP →，则|FQ ||PQ |等于( )A.13B.34C.43 D ．3 答案 B解析 如图，过点P 作准线的垂线交于点H ，由抛物线的定义有|PF |＝|PH |＝m (m >0)，过点Q 作准线的垂线交于点E ，则|EQ |＝|QF |， ∵PM →＝2FP →， ∴|PM |＝2m ，根据△PHM ∽△QEM ， 可得|PH ||PM |＝|QE ||QM |＝12，∴2|EQ |＝|QM |＝|FQ |＋3m . ∴|EQ |＝3m ，即|FQ |＝3m ， ∴|FQ ||PQ |＝3m 3m ＋m ＝34. 易错提醒 焦半径公式和焦点弦面积公式容易混淆，用时要注意使用的条件；数形结合求解时，焦点弦的倾斜角可以为锐角、直角或钝角，不能一律当成锐角而漏解．跟踪演练1 (1)已知A ，B 是过抛物线y 2＝2px (p ＞0)焦点F 的直线与抛物线的交点，O 是坐标原点，且满足AB →＝3FB →，S △OAB ＝23|AB |，则|AB |的值为( )A.92B.29 C ．4 D ．2 答案 A解析 如图，不妨令直线AB 的倾斜角为α，α∈⎝⎛⎭⎫0，π2，∵AB →＝3FB →∴F 为AB 的三等分点， 令|BF |＝t ，则|AF |＝2t ， 由1|BF |＋1|AF |＝2p， 得1t ＋12t ＝2p ⇒t ＝34p ， ∴|AB |＝3t ＝94p ，又|AB |＝2psin 2α， ∴2p sin 2α＝94p ⇒sin α＝223， 又S △AOB ＝23|AB |， ∴p 22sin α＝23|AB |， 即p 2423＝23·94p ⇒p ＝2， ∴|AB |＝92.(2)(多选)已知抛物线C ：x 2＝4y ，焦点为F ，过点F 的直线与抛物线交于A ，B 两点，该抛物线的准线与y 轴交于点M ，过点A ，B 作准线的垂线，垂足分别为H ，G ，如图所示，则下列说法正确的是( )A ．线段AB 长度的最小值为2B ．以AB 为直径的圆与直线y ＝－1相切C ．∠HFG ＝90°D ．∠AMO ＝∠BMO答案 BCD解析 如图，取AB 的中点为C ，作CD ⊥GH ，垂足为D ，当线段AB 为通径时长度最小，为2p ＝4，故A 不正确； ∵直线y ＝－1为准线， ∴|CD |＝12(|AH |＋|BG |)＝12|AB |，故以AB 为直径的圆与准线y ＝－1相切， 故B 正确；又|BF |＝|BG |，∴∠BFG ＝∠BGF ， 又BG ∥FM ， ∴∠BGF ＝∠MFG ， ∴∠BFG ＝∠MFG ， 同理可得∠AFH ＝∠MFH ，又∠BFG ＋∠MFG ＋∠MFH ＋∠AFH ＝180°， ∴FG ⊥FH .即∠HFG ＝90°，故C 正确； 设A (x 1，y 1)，B (x 2，y 2)，∴直线AB ：y ＝kx ＋1，由⎩⎪⎨⎪⎧y ＝kx ＋1，x 2＝4y ，得x 2－4kx －4＝0， ∴x 1x 2＝－4，x 1＋x 2＝4k ， k AM ＋k BM ＝y 1＋1x 1＋y 2＋1x 2＝kx 1＋2x 1＋kx 2＋2x 2＝2k ＋2(x 1＋x 2)x 1x 2＝2k ＋2·4k－4＝0，∴∠AMO ＝∠BMO ，故D 正确．考点二 定点问题核心提炼抛物线方程为y 2＝2px (p >0)，过(2p ，0)的直线与之交于A ，B 两点，则OA ⊥OB ，反之，也成立．例5 如图，已知直线与抛物线x 2＝2py 交于A ，B 两点，且OA ⊥OB ，OD ⊥AB 交AB 于点D ，点D 的坐标为(2,4)，则p 的值为( )A ．2B ．4 C.32 D.52答案 D解析 如图，令AB 与y 轴交于点C ，∵OA ⊥OB ，∴AB 过定点C (0,2p )， 又D (2,4)，∴CD →＝(2,4－2p )，OD →＝(2,4)， ∵OD ⊥AB ， ∴CD →·OD →＝0， 即4＋4(4－2p )＝0， 解得p ＝52.易错提醒 要注意抛物线的焦点位置，焦点不同，定点是不同的；在解答题中用该结论时需证明该结论．跟踪演练2 已知抛物线y 2＝4x ，A ，B 为抛物线上不同两点，若OA ⊥OB ，则△AOB 的面积的最小值为________． 答案 16解析 如图，∵OA ⊥OB ，∴直线AB 过定点(2p ，0)， 即点C 坐标为(4,0)，设直线AB ：x ＝ty ＋4，A (x 1，y 1)，B (x 2，y 2)，联立⎩⎪⎨⎪⎧x ＝ty ＋4，y 2＝4x ⇒y 2－4ty －16＝0，Δ＝16t 2＋64>0，y 1＋y 2＝4t ，y 1y 2＝－16， ∴S △AOB ＝12|OC ||y 1－y 2|＝2|y 1－y 2|＝216t 2＋64，∴当t ＝0时，S min ＝16.专题强化练1．(2022·菏泽模拟)设坐标原点为O ，抛物线y 2＝4x 与过焦点的直线交于A ，B 两点，则OA →·OB →等于( )A.34 B ．－34 C ．3 D ．－3 答案 D解析 方法一 抛物线y 2＝4x 的焦点为F (1,0)， 设直线AB 的方程为x ＝ty ＋1，A (x 1，y 1)，B (x 2，y 2)，由⎩⎪⎨⎪⎧x ＝ty ＋1，y 2＝4x ，得y 2－4ty －4＝0， Δ＝16t 2＋16>0恒成立，则⎩⎪⎨⎪⎧y 1＋y 2＝4t ，y 1y 2＝－4， 所以OA →·OB →＝x 1x 2＋y 1y 2＝y 214·y 224＋y 1y 2＝1616＋(－4)＝－3. 方法二 因为AB 过抛物线的焦点， 设A (x 1，y 1)，B (x 2，y 2)，则x 1x 2＝p 24＝1，y 1y 2＝－p 2＝－4，所以OA →·OB →＝x 1x 2＋y 1y 2＝－3.2.如图，过抛物线y 2＝8x 的焦点F 的直线l 与抛物线交于A ，B 两点，与抛物线准线交于C 点，若B 是AC 的中点，则|AB |等于( )A ．8B ．9C ．10D ．12答案 B解析 如图所示，令|BF |＝t ， 则|BB ′|＝t ， 又B 为AC 的中点， ∴|AA ′|＝|AF |＝2t ， ∴|BC |＝|AB | ＝|AF |＋|BF |＝3t ， 又△CBB ′∽△CFE ， ∴|BC ||CF |＝|BB ′||FE |， 即3t 3t ＋t ＝t p⇒t ＝34p ，∴|AB |＝3t ＝94p ＝9.3．倾斜角为π4的直线l 交抛物线C ：y 2＝2px (p >0)于A ，B 两点，且OA ⊥OB ，S △AOB ＝85，则抛物线C 的方程为( ) A ．y 2＝2xB ．y 2＝4xC ．y 2＝42xD ．y 2＝8x答案 B解析 ∵OA ⊥OB ， ∴直线过定点(2p ，0) 设直线l 的方程为x ＝y ＋2p ， 设A (x 1，y 1)，B (x 2，y 2)，联立⎩⎪⎨⎪⎧x ＝y ＋2p ，y 2＝2px ，得y 2－2py －4p 2＝0，Δ＝4p 2－4×(－4p 2)＝20p 2>0， ∴y 1＋y 2＝2p ，y 1y 2＝－4p 2， S △AOB ＝12·2p ·|y 1－y 2|＝p (y 1＋y 2)2－4y 1y 2＝p ·4p 2＋16p 2＝25p 2＝85， ∴p ＝2，∴抛物线C 的方程为y 2＝4x .4．直线l 过抛物线y 2＝6x 的焦点F ，交抛物线于A ，B 两点，且|AF |＝3|BF |，过A ，B 分别作抛物线C 的准线的垂线，垂足分别为A ′，B ′，则四边形ABB ′A ′的面积为( ) A ．4 3 B ．8 3 C ．16 3 D ．32 3 答案 C解析 不妨令直线l 的倾斜角为θ，则|AF |＝p 1－cos θ＝31－cos θ，|BF |＝p 1＋cos θ＝31＋cos θ，又|AF |＝3|BF |， ∴31－cos θ＝3·31＋cos θ，解得cos θ＝12，又θ∈[0，π)，∴θ＝π3，∴|AF |＝31－cos θ＝6，|BF |＝31＋cos θ＝2， ∴|AA ′|＝6，|BB ′|＝2，∴|A ′B ′|＝|AB |sin θ＝8×32＝43， ∴S 四边形ABB ′A ′＝12×(2＋6)×43＝16 3. 5．(多选)(2022·聊城模拟)已知抛物线C ：y 2＝2px (p >0)的焦点F 到准线的距离为2，过F 的直线l 交抛物线C 于A ，B 两点，则( )A ．C 的准线方程为x ＝－2B ．若|AF |＝4，则|OA |＝21C ．若|AF |·|BF |＝4p 2，则l 的斜率为±33D ．过点A 作准线的垂线，垂足为H ，若x 轴平分∠HFB ，则|AF |＝4答案 BCD解析 因为抛物线C ：y 2＝2px (p >0)的焦点F 到准线的距离为2，所以p ＝2，所以抛物线方程为y 2＝4x ，则焦点F (1,0)，准线为x ＝－1，故A 错误；若|AF |＝4，则x A ＝3，所以y 2A ＝4x A＝12， 所以|OA |＝x 2A ＋y 2A ＝21，故B 正确；设直线AB 的倾斜角为α，α∈(0，π)，|AF ||BF |＝p 1－cos α·p 1＋cos α＝p 2sin 2α＝4p 2， ∴sin 2α＝14， ∴sin α＝12， ∴α＝30°或150°，∴tan α＝±33，故C 正确； 对于D ，若x 轴平分∠HFB ，则∠OFH ＝∠OFB ，又AH ∥x 轴，所以∠AHF ＝∠OFH ＝∠OFB ＝∠AFH ，所以HF ＝AF ＝AH ，所以x A ＋x H 2＝x F ，即x A ＝3， 所以|AF |＝x A ＋1＝4，故D 正确．6．(多选)(2022·武汉模拟)斜率为k 的直线l 经过抛物线C ：y 2＝2px (p >0)的焦点F ，且与抛物线C 相交于A ，B 两点，点A 在x 轴上方，点M (－1，－1)是抛物线C 的准线与以AB 为直径的圆的公共点，则下列结论正确的是( )A ．p ＝2B ．k ＝－2C ．MF ⊥ABD.|F A ||FB |＝25 答案 ABC解析 由题意知，抛物线C 的准线为x ＝－1，即p 2＝1，解得p ＝2， 故选项A 正确；∵p ＝2，所以抛物线C 的方程为y 2＝4x ，其焦点为F (1,0)，∵以AB 为直径的圆与准线相切，∴点M (－1，－1)为切点，∴圆心的纵坐标为－1，即AB 中点的纵坐标为－1，设AB ：x ＝ty ＋1，联立⎩⎪⎨⎪⎧x ＝ty ＋1，y 2＝4x ， 得y 2－4ty －4＝0，Δ＝16t 2＋16>0，∴y 1＋y 2＝4t ＝－2，∴t ＝－12，即k ＝－2，故选项B 正确； ∵k ＝－2，k MF ＝－1－0－1－1＝12，k MF·k ＝－1， ∴MF ⊥AB ，故选项C 正确；过A 作AA 1⊥x 轴，过B 作BB 1⊥x 轴，抛物线的准线交x 轴于点C ，设∠BFB 1＝θ，∴|BF |＝p 1－cos θ， |AF |＝p 1＋cos θ， 又p ＝2，k ＝－2，则cos θ＝55， ∴|F A ||FB |＝5－55＋5＝(5－5)225－5＝30－10520＝3－52， 故选项D 错误．7．已知抛物线y 2＝4x 的焦点为F ，过点F 的直线l 交抛物线于M ，N 两点，且|MF |＝2|NF |，则直线l 的斜率为______．答案 ±2 2解析 由抛物线的焦点弦的性质知1|MF |＋1|NF |＝2p＝1， 又|MF |＝2|NF |，解得|NF |＝32，|MF |＝3， ∴|MN |＝92， 设直线l 的倾斜角为θ，∴k ＝tan θ，又|MN |＝2p sin 2θ， ∴4sin 2θ＝92， ∴sin 2θ＝89，∴cos 2θ＝19， ∴tan 2θ＝8，∴tan θ＝±22，故k ＝±2 2.8.(2022·攀枝花模拟)如图所示，已知抛物线C 1：y 2＝2px 过点(2,4)，圆C 2：x 2＋y 2－4x ＋3＝0.过圆心C 2的直线l 与抛物线C 1和圆C 2分别交于P ，Q ，M ，N ，则|PM |＋4|QN |的最小值为________．答案 13解析 由题设知，16＝2p ×2，则2p ＝8，故抛物线的标准方程为y 2＝8x ，则焦点F (2,0)， 由直线PQ 过抛物线的焦点，则1|PF |＋1|QF |＝2p ＝12， 圆C 2：(x －2)2＋y 2＝1的圆心为(2,0)，半径为1， |PM |＋4|QN |＝|PF |－1＋4(|QF |－1)＝|PF |＋4|QF |－5＝2(|PF |＋4|QF |)⎝⎛⎭⎫1|PF |＋1|QF |－5＝2×⎝⎛⎭⎫|PF ||QF |＋4|QF ||PF |＋5≥4|PF ||QF |·4|QF ||PF |＋5＝13， 当且仅当|PF |＝2|QF |时，等号成立，故|PM |＋4|QN |的最小值为13.。

当前位置：首页>>高中数学>>学生中心>>解题指导圆锥曲线有关焦点弦的几个公式及应用湖北省阳新县高级中学邹生书如果圆锥曲线的一条弦所在的直线经过焦点，则称此弦为焦点弦。

圆锥曲线的焦点弦问题涉及到离心率、直线斜率（或倾斜角）、定比分点（向量）、焦半径和焦点弦长等有关知识。

焦点弦是圆锥曲线的“动脉神经”，集数学知识、思想方法和解题策略于一体，倍受命题人青睐，在近几年的高考中频频亮相，题型多为小题且位置靠后属客观题中的压轴题，也有作为大题进行考查的。

本文介绍圆锥曲线有关焦点弦问题的几个重要公式及应用，与大家交流。

定理1已知点是离心率为的圆锥曲线的焦点，过点的弦与的焦点所在的轴的夹角为，且。

（1）当焦点内分弦时，有；（2）当焦点外分弦时（此时曲线为双曲线），有。

证明设直线是焦点所对应的准线，点在直线上的射影分别为，点在直线上的射影为。

由圆锥曲线的统一定义得，，又，所以。

（1）当焦点内分弦时。

如图1，，所以。

图1（2）当焦点外分弦时（此时曲线为双曲线）。

如图2，，所以。

图2评注特别要注意焦点外分焦点弦（此时曲线为双曲线）和内分焦点弦时公式的不同，这一点很容易不加区别而出错。

例1（2009年高考全国卷Ⅱ理科题）已知双曲线的右焦点为，过且斜率为的直线交于两点。

若，则的离心率为（）解这里，所以，又，代入公式得，所以，故选。

例2（2010年高考全国卷Ⅱ理科第12题）已知椭圆的离心率为。

过右焦点且斜率为的直线于相交于两点，若，则（）解这里，，设直线的倾斜角为，代入公式得，所以，所以，故选。

例3 （08高考江西卷理科第15题）过抛物线的焦点作倾斜角为的直线，与抛物线交于两点（点在轴左侧），则有＿＿＿＿图3解如图3，由题意知直线与抛物线的地称轴的夹角，当点在轴左侧时，设，又，代入公式得，解得，所以。

例4（2010年高考全国卷Ⅰ理科第16题）已知是椭圆的一个焦点，是短轴的一个端点，线段的延长线交于点，且，则的离心率为＿＿＿解设直线与焦点所在的轴的夹角为，则，又，代入公式得，所以。

抛物线焦点弦问题河北省武安市第一中学郅武强抛物线焦点弦问题较多，由焦点引出弦的几何性较集中，现总结如下：一．弦长问题：例斜率为1的直线经过抛物线24y x =的焦点，与抛物线相交A .B两点，求线段AB 的长。

分析：利用弦长公式12d x =-能解此题，但运算量较大也较复杂，如果能够运根据抛物线的定义，11AF x =+同理 21BF x =+于是得122AB AF BF x x =+=++由题已知{214y x y x=-=消去y 得2610x x -+=故126x x += ∴628AB =+= 注：焦点弦在标准抛物线方程下的计算公式：12AB x x p =++或12AB y y p=++。

二. 通径最短问题：例：已知抛物线的标准方程为22y px =，直线l 过焦点，和抛物线交与A.B 两点，求AB 的最小值并求直线方程。

解：①如果直线l 的斜率不存在，则直线l 的方程为2px =2A B p =②如果斜率存在，不妨设斜率为k ，则直线的方程为(2p y k x =-，与抛物线方程联立方程组得22( 2y pxp y k x ==-⎧⎨⎩消去y 得22222(2 04k p k x k p p x -++=若0k ≠ 则222440k p p ∆=+>1222px x p k +=+则1222222p p AB x x p p p p k k =++=++=+当k →∞时 AB最小即min 2AB p = 此时 2px =三．两个定值问题：例：过抛物线22y px =的焦点的一条直线和抛物线相交，两个焦点的横、纵坐标为1x 、2x 、1y 、2y ，求证：2114p x y =，212y y p =-。

证明：①联立22( 2y px p y k x ==-⎧⎨⎩消去y 得22222(2 0(04k p k x k p p x k -++=≠2124p x x =同理消去y 可得 212y y p =-；②斜率为0时，直线与抛物线不能有两个交点；③斜率不存在时，2114p x y = ，212y y p =-同样是定值；从上所述：2114p x y =，212y y p =-四．一个特殊直角问题：过抛物线22(0 y px P =>的焦点F 的直线与抛物线交与A 、B 两点，若点A 、B 在抛物线的准线上的射影分别是1A ，1B 求证：1190A FB ︒∠=。

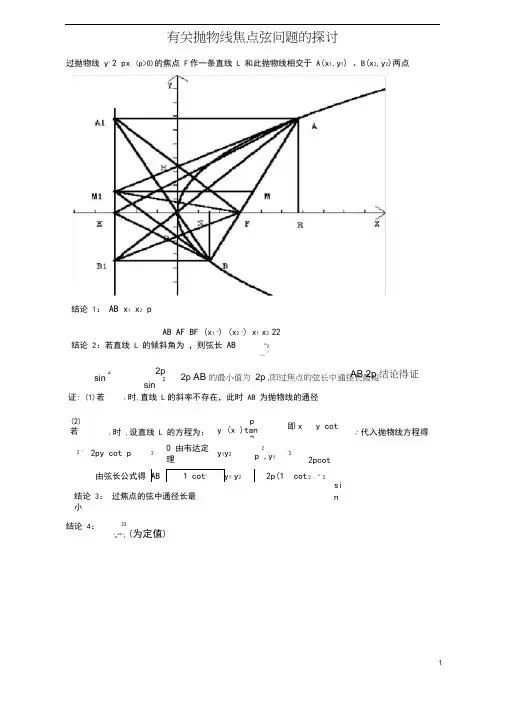
有关抛物线焦点弦问题的探讨过抛物线 y 22 px (p>0)的焦点 F 作一条直线 L 和此抛物线相交于 A (x 1,y 1) 、B (x 2,y 2)两点结论 1： AB x 1 x 2 pAB AF BF (x 1 p) (x 2 p) x 1 x 2 22结论 2：若直线 L 的倾斜角为 ，则弦长 AB 2p 2sin2结论 4：23S ABoAB p8(为定值)(2)若2时 ,设直线 L 的方程为： py (x )tan2 即xy cot2p代入抛物线方程得2 y2py cot p 2 0 由韦达定理y 1y 2 2 p ,y 1y22pcot2 )2p )2由弦长公式得 AB 1 cot 2y 1 y 2 2p(1 cot证: (1)若2时,直线 L 的斜率不存在，此时 AB 为抛物线的通径si n结论 3： 过焦点的弦中通径长最小 AB 2p 结论得证 2sin2p 2sin2p AB 的最小值为 2p ,即过焦点的弦长中通径长最短同理 B 1FOB 1FBA 1FB 1 90A 1FB 1 F2结论 8：（1）AM 1 BM 1 （2）M 1F AB （3） M 1F AF BF（4）设 AM 1 与 A 1F 相交于 H ，M 1B 与 FB 1相交于 Q 则M 1，Q ，F ，H 四点共圆 （5） AM 12M 1B 24M 1M 2证：由结论（ 6）知 M 1 在以 AB 为直径的圆上 AM 1 BM 1A 1FB 1为直角三角形， M 1 是斜边 A 1 B 1 的中点A 1M 1 M 1F M1FA 1M1A 1FAA 1F AFA 1AA 1FFA 1MAA 1M190AFA 1A1FM190M 1FABM 1F2AFBFAM 1BM 1 AM1B 90又 A 1FB 1FA 1FB 1 90 所以 M 1，Q ， F,H 四点共圆， AM 1 2M 1B 2AB 22 2 2 2AF BF 2AA 1 BB 1 22MM 1 24MM 1 2结论 9： （1） A 、O 、B 1 三点共线 （ 2）B ，O ，A 1 三点共线（3）设直线 AO 与抛物线的准线的交点为 B 1，则 BB 1平行于 X 轴（ 4）设直线 BO 与抛物线的准线的交点为 A 1，则 AA 1平行于 X 轴S OAB SOBF1S 0AFOFBF 1sin 2OF AF sin OF 2S OABAB结论 5： （1） 证x 1AFP 3y 1y 22y1 2p ,x 2BF 2p 2sinOF AB sinp22psin2 sin 22 p2sin(2) x 1x 2=2 y22px 1x 2(y 1y 2)24P 2P 2结论 6：以 AB 证：设 M 为 AB 的中点，过 A 点作准线的垂线 过 M 点作准线的垂线 MM 1，由梯形的中位线性质和抛物线的定义知 为直径的圆与抛物线的准线相切AA 1， 过 B 点作准线的垂线 BB 1，MM 1结论 7：连接 A 1F 、 AA 1 AF,AA 1 BB 1 AF BF22B 1 F 则 A 1FAA 1F B 1FAB 2故结论得证AFA 1 AA 1 //OF AA 1FA 1FO A 1FO A 1FA41E,因为直线 L 的倾斜角为证：因为 k oAy1 x1y12 y12p,k oBoB 1y 11y2 p2y2，而 y 1y 2 p2 p2p2所以 k oA2p2 p y22y 2 pk oB 1所以三点共线。

抛物线的常见结论一、知识点总结 1. 抛物线的弦长公式2122122124)(11x x x x k x x k l -+•+=-+=，其中k 是弦所在直线的斜率，21,x x 是交点的横坐标，本表达式不包含斜率不存在的情况。

2122122124)(11y y y y m y y m l -+•+=-+=，其中弦长所在直线方程为b my x +=，21,y y 是交点的纵坐标，本表达式包含斜率不存在的情况。

2. 抛物线的焦点弦对于抛物线，022>=p px y ，，倾斜角为α的直线过抛物线的焦点，与抛物线交于A ，B 两点，过A,B 做抛物线准线的垂线，垂足分别为C,D ，那么有：①221221,4p y y p x x -== ABF CDOα由⎪⎩⎪⎨⎧+==222p my x pxy 得0222=--p pmy y （＊），因此⎪⎩⎪⎨⎧==-=44)(2222121221p p y y x x p y y ②焦点弦长p x x AB ++=21，焦点弦长α2sin 2P AB =ααsin 4)(sin 2122121y y y y y y AB -+=-=，结合（＊）式与αtan 1=m 得： ααααααααααsin sin sin sin cos 2sin 1tan 12sin 4tan 4sin 4422222222222+=+=+=+=p p p p p m p ABααα22sin 2sin sin 12p p ==③PBF AF 211=+ 简单证明如下:p p p y y p y y PBF AF BF AF BF AF 222sin sin sin 211221212====+=+ααα ④焦点三角形面积αsin 22P S =简单证明如下：以AB 为底，以O 到AB 的距离为高，该三角形面积课表示为：ααααsin 2sin 2sin 221sin 2122p p p OF AB S AOB=⨯⨯== ⑤焦点弦相关的几何关系： a. 以AF/BF 为直径的圆与y 轴相切b. 以AB 为直径的圆与准线相切，切点与焦点连线垂直于AB.c. 以CD 为直径的圆与AB 相切d. A,B 在准线上的投影对F 的张角为90°，︒=∠90CFDe.以A,B 为切点分别做两条切线，两切线的交点在准线上；在准线上取一点做抛物线的切线，两切点所在直线一定经过抛物线的焦点。

焦点弦公式例题
焦点弦公式是求解椭圆、双曲线或抛物线上经过一个焦点的弦的长度。

这里提供一个抛物线的焦点弦公式的例题。

例题：已知抛物线的方程为y^2 = 4px（p > 0），焦点为F(p, 0)，过焦点F 作直线l 交抛物线于A、B 两点，求弦AB 的长度。

解题步骤：
1.设点并写出方程：设直线l 的方程为x = my + p，与抛物线方
程y^2 = 4px 联立。

2.联立方程求解：联立方程组
{x=my+py2=4px
得到：
y2−4pmy−4p2=0
3.应用韦达定理：设交点A(x1, y1)，B(x2, y2)，根据韦达定理，我
们有：
y1+y2=4pm
y1y2=−4p2
4.计算弦长：弦AB 的长度可以用以下公式计算：
∣AB∣=(x2−x1)2+(y2−y1)2
由于y 坐标已解出，我们可以利用y 坐标的差来求弦长。

利用抛物线性质，弦长也可以表示为：
∣AB∣=x1+x2+p
将x 坐标表示为y 坐标的函数，代入上述公式中，得到：
∣AB∣=m(y1+y2)+2p=4p2m2+2p
5.简化表达式：考虑到弦AB 经过焦点F，其倾斜角为θ（θ ≠
90°），则斜率m = tanθ。

因此，弦长公式可以进一步简化为：∣AB∣=sin2θ2p
当θ = 90° 时，弦AB 为通径，此时|AB| = 2p。

这个例题展示了如何使用抛物线的性质和联立方程的方法来求解焦点弦的长度。

对于椭圆和双曲线的焦点弦长度计算，也有类似的方法，但具体公式会有所不同。

在求解时，需要注意各种可能的特殊情况，并相应地调整解题步骤。

抛物线焦点弦长公式二级结论
抛物线焦点弦长公式是：<a>AB=2*a*sqrt{c^2-(b^2)/4a^2}</a>
一、抛物线焦点弦长定义
1、抛物线焦点弦（AB）是抛物线的一部分，它由焦点之间的两个点构成，它们分别为上抛物线上的焦点F1和下抛物线上的焦点F2；
2、抛物线焦点弦的长度表示两个焦点连线的长度，即两点F1，F2之间的直线距离；
二、抛物线焦点弦长公式
抛物线焦点弦长公式是：AB=2*a*sqrt{c^2-(b^2)/4a^2}，其中a为抛物线顶点到水平轴的距离，b为抛物线顶点到垂线的距离，c为抛物线焦点到垂线的距离。

三、抛物线焦点弦长使用
1、由抛物线焦点弦长公式可知，我们可以利用这个公式求出若干特定抛物线的焦点弦的长度；
2、抛物线焦点弦的长度也可用于解决日常生活中的物理问题，比如可以确定抛物线上任意两点之间的距离等；
四、抛物线焦点弦长结论
抛物线焦点弦长公式可以使用来求解抛物线的焦点弦的长度，而且该长度也可以用于解决实际中的一些物理问题。

有关抛物线焦点弦问题的探讨过抛物线px y 22=(p>0)的焦点F 作一条直线L 和此抛物线相交于A ),(11y x 、B ),(22y x 两点两点结论1：px x AB ++=21p x x px px BF AF AB ++=+++=+=2121)2()2( 结论2：若直线L 的倾斜角为θ，则弦长θ2sin 2pAB =证:(1)若2πθ= 时,直线L 的斜率不存在，此时AB 为抛物线的通径,结论得证∴=∴p AB 2(2)若2πθ≠时,设直线L 的方程为：θtan )2(px y -=即2cot py x +⋅=θ 代入抛物线方程得cot 222=-⋅-p py y θ由韦达定理θcot 2,21221p y y p y y =+-= 由弦长公式得θθθ22212sin 2)cot 1(2cot 1p p y y AB =+=-+= 结论3： 过焦点的弦中通径长最小p p 2sin 21sin 22≥∴≤θθΘ∴AB 的最小值为p 2,即过焦点的弦长中通径长最短. 结论4： )(832为定值p AB S oAB =∆()8sin 2sin sin 2221sin 21sin 21sin 21sin 2132220P AB S p pp AB OF BF AF OF AF OF BF OF S S S OAB AF OBF OAB =∴=⋅⋅⋅=⋅⋅=+⋅=⋅⋅+⋅⋅=+=∆∆∆∆θθθθθϑθ结论5： (1) 221p y y -= (2) x 1x 2=42p证44)(,2,22222121222211P P y y x x p y x p yx ==∴==Θ 结论6：以AB 为直径的圆与抛物线的准线相切 证：设M 为AB 的中点，过A 点作准线的垂线AA 1， 过B 点作准线的垂线BB 1，过M 点作准线的垂线MM 1，由梯形的中位线性质和抛物线的定义知，由梯形的中位线性质和抛物线的定义知 222111ABBF AF BBAA MM =+=+=故结论得证故结论得证 结论7：连接A 1F 、B 1 F 则 A 1F ⊥B 1FFA A FO A FO A F AA OF AA AFA F AA AF AA 11111111//,∠=∠∴∠=∠∴∠=∠∴=ΘΘ 同理︒=∠∴∠=∠901111FB A FB B FO B ∴A 1F ⊥B 1 F 结论8：（1）AM 1⊥BM 1 （2）M 1F ⊥AB （3）BF AF F M ⋅=21 （4）设AM 1 与A 1F 相交于H ，M 1B 与 FB 1相交于Q 则M 1，Q ，F ，H 四点共圆（5）2121214M M B M AM =+证：由结论（6）知M 1 在以AB 为直径的圆上∴ AM 1⊥BM 1Θ11FB A ∆为直角三角形，为直角三角形，M 1 是斜边A 1 B 1 的中点的中点 111111111AFA F AA F A M FA M F M M A ∠=∠∠=∠∴=∴Θ︒=∠=∠+∠9011111M AA M FA F AA Θ ︒=∠+∠∴90111FM A AFA∴M 1F ⊥ABBF AF F M ⋅=∴21 ΘAM 1⊥BM 1 F B F A 90111⊥︒=∠∴Θ又B AM︒=∠∴90FB A 11所以M 1，Q ，F,H 四点共圆，22121AB B M AM =+()()()2121211242MM MM BB AA BFAF ==+=+=结论9： （1）、A O 、B 1 三点共线 （2）B ，O ，A 1 三点共线 （3）设直线AO 与抛物线的准线的交点为B 1，则BB 1平行于X 轴（4）设直线BO 与抛物线的准线的交点为A 1，则AA 1平行于X 轴证：因为p y p y k y p py y x y k oB oA 2212111122,221-=-====，而221p y y -= 所以122222oB oAk p y y p p k =-=-=所以三点共线。

抛物线弦长公式引言在几何学和数学中，抛物线是一种常见的曲线形状。

抛物线具有许多重要的性质和应用，其中一个重要的性质是它的弦长，也称为抛物线弦长。

本文将介绍抛物线弦长的概念和计算方法，并提供一个用于计算抛物线弦长的公式。

抛物线的定义抛物线是一种平面曲线，定义为所有到一个固定点（焦点）和到一条固定直线（准线）距离恒等的点的轨迹。

抛物线有一个特殊的直线对称轴，过焦点和准线垂直的轴线，称为对称轴。

抛物线的形状由焦点和准线的位置所决定。

抛物线弦长的定义抛物线弦长是抛物线上两个点之间的距离，这两个点是由一个平行于对称轴的线段所确定的。

通常情况下，抛物线弦长是通过两个焦点之间的直线段来确定的。

由于抛物线的对称性，抛物线上任意两个点之间的弦长都是相等的。

抛物线弦长的计算方法对于任意给定的抛物线，我们可以使用以下公式来计算抛物线弦长：L = 2a sin(theta)其中，L是抛物线弦长，a是抛物线的焦点到对称轴的距离，theta是与对称轴垂直的线段与抛物线对称轴的夹角。

在这个公式中，a是抛物线的一个关键参数，称为焦半径或焦距，表示焦点到对称轴的距离。

theta是另一个关键参数，表示焦点到弦的线段与对称轴的夹角。

抛物线弦长公式的推导要理解抛物线弦长公式的推导，我们首先需要了解抛物线的一些基本性质。

•抛物线的标准方程为y = ax^2 + bx + c，其中a，b和c是常数。

•抛物线的焦点的坐标为(h, k)。

•抛物线的准线方程为y = -h + k。

•抛物线的对称轴方程为x = h。

现在，假设我们有一个抛物线，焦点位于原点(0,0)处，对称轴与y轴对齐。

我们要计算抛物线上两个点之间的距离，即弦长。

抛物线弦长抛物线弦长从上图可以看出，我们可以使用三角函数来计算抛物线弦长。

用theta表示线段OP与对称轴的夹角，线段OP与抛物线对称轴的夹角是45度，假设OP的长度为d。

根据三角函数的定义，在直角三角形POQ中，sin(theta) = a/d。

专题07 圆锥曲线的第二定义与焦点弦【突破总分值数学之秒杀技巧与答题模板】：焦点弦定义：过焦点的直线与曲线相交于两点A 、B ，弦AB 叫做曲线的焦点弦。

秒杀题型一：椭圆与双曲线焦点弦中常考的秒杀公式：①焦点弦长公式：θ222cos 12e a b -(θ为直线与焦点所在轴的夹角)，通径：22b a (最短焦点弦)； ②焦点弦被焦点分成两局部,m n ，那么2112am n b+=(定值)(取通径即可)。

③BF AF λ=，那么有11cos +-=λλθe (θ为直线与焦点所在轴的夹角)。

秒杀题型二：抛物线的焦点弦中常考的秒杀公式：①过抛物线)0(22>=p px y 焦点的直线交抛物线于A 、B 两点，那么:2p y y B A -=,42p x x B A =。

(焦点在y 轴上的性质比照给出。

)引伸:M (,0)a (0)a >在抛物线22(0)y px p =>的对称轴上，过M 的直线交抛物线于两点。

1122(,),(,)A x y B x y ,12.y y =2pa -(定值)。

②α2sin 2||pAB =(α是直线AB 与焦点所在轴的夹角)=12x x p ++(焦点在x 轴正半轴上)(其它三种同理可以推导)，焦点弦中通径(垂直于对称轴的焦点弦,长为2p )最短。

③BF AF λ=，那么有11cos +-=λλθ，θcos 1-=p AF ，θcos 1+=p BF (θ为直线与焦点所在轴的夹角)。

④面积:θsin 22p S AOB=∆，θ32sin 2p S AMNB =(θ是直线AB 与焦点所在轴的夹角)。

⑤以AB 为直径的圆与准线MN 相切，切点为MN 中点Q ，BQ AQ ,分别是抛物线的切线，并且分别是NBA MAB ∠∠,的角平分线。

⑥以MN 为直径的圆与AB 相切，切点为焦点F 。

⑦以焦半径为直径的圆与y 轴相切。

⑧N O A ,,三点共线,M O B ,,三点共线。

高中数学中的四大类弦长公式一、平面直角坐标中的全场通用弦长公式1、已知两点坐标：()11,y x A ，()22,y x B ，则()()221221y y x x AB -+-=2、已知直线上两点：若()11,y x A ，()22,y x B 两点在直线b kx y +=（直线的斜率存在并且不为0）上，则ak x x k AB ∆+=-+=221211（∆,,21x x 是02=++c bx ax 的两根和判别式） ak y y k AB ∆+=-+=22121111（∆,,21y y 是02=++c by ay 的两根和判别式）注：以上公式适用于直线与曲线相交，将直线与曲线联立但不易求出交点坐标 时，采用设而不求思想的解决弦长问题，以上公式的证明会用到韦达定理）二、平面直角坐标中特殊曲线（例如：圆，抛物线，椭圆）中的弦长公式1、直线0:=++C By Ax l 与圆()()222:r b y a x M =-+-相交于B A ,，则222d r AB -=（其中22BA C Bb Aa d +++=为圆心),(b a M 到直线l 的距离）注：此公式证明需用垂径定理2、抛物线中的焦点弦弦长公式，过抛物线交点F 直线l 与抛物线相交的弦长,BF AF AB += ①α221sin 2px x p AB =++=（其中抛物线开口向右，方程为px y 22=）②)(21x x p AB +-=（其中抛物线开口向左，方程为px y 22-=） ③21y y p AB ++=（其中抛物线开口向上，方程为py x 22=） ④)(21y y p AB +-=（其中抛物线开口向下，方程为py x 22-=） 注：此公式的证明需用到抛物线的定义和焦半径公式.3、椭圆中的焦点弦的弦长公式,BF AF AB +=①过椭圆)0(12222>>=+b a by a x 的左焦点)0,(1c F -的直线l 与椭圆相交于()11,y x A ，()22,y x B 两点，则()212x x e a AB ++=.②过椭圆)0(12222>>=+b a by a x 的左焦点)0,(2c F 的直线l 与椭圆相交于()11,y x A ，()22,y x B 两点，则()212x x e a AB +-=.③过椭圆)0(12222>>=+b a bx a y 的左焦点)0(1c F -，的直线l 与椭圆相交于 ()11,y x A ，()22,y x B 两点，则()212y y e a AB ++=.④过椭圆)0(12222>>=+b a by a x 的左焦点),0(2c F 的直线l 与椭圆相交于()11,y x A ，()22,y x B 两点，则()212y y e a AB +-=.注：此公式的证明需用到椭圆的第二定义和焦半径公式.三、直线标准参数方程下的弦长公式过定点),(00y x P ，倾斜角为α的直线l 的参数方程⎩⎨⎧+=+=ααsin cos 00t y y t x x (t 为参数). 参数t 的几何意义为： t 为直线上任一点(,)x y 到定点00(,)x y 的数量；即：直线l 上的动点()()ααsin ,cos ,00t y t x M y x M ++=到点),(00y x P 的距离等于t .设点B A 、对应的参数分别为,,21t t 则有： ①2121,,t t AB t PB t PA -=== ②AB 中点M 对应的参数为221t t +，则.221t t PM +=证明：∵A 对应的参数分别为1t ∴()ααsin ,cos 1010t y t x A ++, ∴ ()()()()1212120102010sin cos sin cos t t t y t y x t x PA =+=-++-+=αααα同理2t PB =,21t t AB -=还有一些可能会用到的公式,他们都可通过以上两个结论+绝对值的运算而得：例如：③⎩⎨⎧<->+=+=+0,,2121212121t t t t t t t t t t PB PA ;⎩⎨⎧<+>-=-=-0,,2121212121t t t t t t t t t t PB PA④ 若AB 的中点为P ,则021=+t t .（∵AB 中点对应的参数为221t t +,P 对应的参数为0）过定点),(00y x P 的直线l 的参数方程也可表示为:⎩⎨⎧+=+=bt y y atx x 00(b a ,是常数,t 为参数).设点N M 、对应的参数分别为21,t t ,即()()20201010,,,bt y at x N bt y at x M ++++则有：①122t b a PM +=，222t b a PN +=，()2122t t b a PN PM +=⋅②Aba t tb a MN ∆+=-+=222122（其中21,t t 是方程02=++C Bt At 的两根）③⎩⎨⎧<->+=+=+0,,2121212121tt t t t t t t t t PN PM ; ⎪⎩⎪⎨⎧<++>-+=-+=-0,0,2121222121222122t t t t b a t t t t b a t t b a PN PM④ 若MN 的中点为P ,则021=+t t .（∵MN 中点对应的参数为221t t +,P 对应的参数为0）四、极坐标系中的弦长公式：()()2211,,,θρθρB A①若21θθ=，则21ρρ-=AB②若21θθ≠，则()21212221cos 2θθρρρρ--+=AB ，()2121sin 21θθρρ-=∆OAB S。