2019-2020学年(浙江专版)高考数学一轮复习(回扣主干知识+提升学科素养)第八章 第七节 抛物线教案 文.doc
- 格式:doc
- 大小:268.60 KB
- 文档页数:4

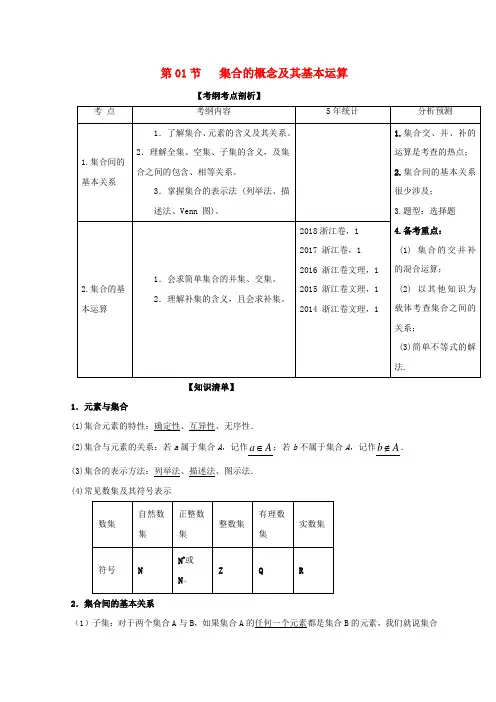
第01节 集合的概念及其基本运算【考纲考点剖析】【知识清单】1.元素与集合(1)集合元素的特性:确定性、互异性、无序性.(2)集合与元素的关系:若a 属于集合A ,记作a A ∈;若b 不属于集合A ,记作b A ∉. (3)集合的表示方法:列举法、描述法、图示法. (4)常见数集及其符号表示2.集合间的基本关系(1)子集:对于两个集合A 与B ,如果集合A 的任何一个元素都是集合B 的元素,我们就说集合A 包含于集合B ,或集合B 包含集合A ,也说集合A 是集合B 的子集。
记为A B ⊆或B A ⊇. (2)真子集:对于两个集合A 与B ,如果A B ⊆,且集合B 中至少有一个元素不属于集合A ,则称集合A 是集合B 的真子集。
记为A B ⊂≠.(3)空集是任何集合的子集, 空集是任何非空集合的真子集.(4)若一个集合含有n 个元素,则子集个数为个,真子集个数为21n -. 3.集合的运算(1)三种基本运算的概念及表示(2)三种运算的常见性质A A A =, A ∅=∅, AB B A =, A A A =, A A ∅=, A B B A =.(C A)A U U C =,U C U =∅,U C U ∅=.A B A A B =⇔⊆,A B A B A =⇔⊆,()U U U C A B C A C B =,()U U U C AB C A C B =.【重点难点突破】考点1 集合的概念【1-1】【2018年全国卷II 理】已知集合,则中元素的个数为A. 9B. 8C. 5D. 4 【答案】A【1-2】若集合{}1A x x =-,则( )A. 3A -∈B. 2A -∈C. 1A -∈D. 0A ∈ 【答案】D 【解析】{}1A x x =-集合就是由全体大于的数构成的集合,显然01>-,故0A ∈ 故选 【领悟技法】与集合元素有关问题的思路:(1)确定集合的元素是什么,即确定这个集合是数集还是点集. (2)看这些元素满足什么限制条件.(3)根据限制条件列式求参数的值或确定集合元素的个数,但要注意检验集合是否满足元素的互异性. 【触类旁通】【变式一】【2017浙江嘉兴一中模拟】若集合{}1,2,3A =,(){},40,,B x y x y x y A =+-∈,则集合中的元素个数为( ) A. 9 B. 6 C. 4 D. 3 【答案】D【解析】,x y A ∈的数对共9对,其中()()()2,3,3,2,3,3满足40x y +->,所以集合中的元素个数共3个. 【变式二】设,,集合,那么与集合的关系是( ) A. B. C. D.【答案】B 【解析】,即,,即a =3,b =π,故x ∈M ,yM , 故选:B.考点2 集合间的基本关系【2-1】【2017届浙江省杭州市第二中学5月仿真】若集合{}A x R ==∈,{}1,B m =,若A B ⊆,则的值为()A. 2B. -2C. -1或2D. 2或 【答案】A【解析】{}2A =,由A B ⊆可知,2m =,故选A 。





浙江专版高考数学一轮复习回扣主干知识提升学科素养函数模型及其应用教案文一、教学目标1.理解函数模型的概念及其应用;2.掌握一些常见的函数模型及其特点;3.能够运用函数模型解决实际问题;4.培养学生对数学的思维能力和创造性思维。
二、教学重点1.函数模型的概念;2.常见的函数模型及其特点;3.函数模型的应用。
三、教学过程Step 1 引入1.引出函数模型的概念,通过图像、表格等形式,让学生感受函数的变化规律。
Step 2 函数模型的概念及其特点1.通过实例引出函数的定义及其特点,让学生理解函数的基本概念;2.总结函数的特点:定义域、值域、增减性、奇偶性、周期性等。
Step 3 常见的函数模型及其特点1.引导学生观察和总结常见的函数模型及其特点:线性函数、二次函数、指数函数、对数函数等;2.利用实例分析函数模型的定义域、值域、图像等特点,并探讨其应用。
Step 4 函数模型的应用1.实例分析:利用函数模型解决实际问题;2.引导学生自主思考并运用函数模型解决实际问题,提高学生的问题解决能力;3.总结常见的函数模型在实际问题中的应用,如经济学、物理学、生物学等。
四、教学方法1.演示法:通过实例演示,让学生感受函数的变化规律;2.归纳法:引导学生观察和总结函数模型的特点;3.实践法:让学生自主思考并运用函数模型解决实际问题。
五、教学评价1.收集学生解答问题的过程和结果,评价学生的分析和解决问题的能力;2.对学生进行小组讨论,互相评价和反馈,加强学生的合作意识和团队精神。
六、教学拓展1.将函数模型与其他学科进行结合,如物理学中的运动学模型、生物学中的增长模型等;2.通过案例分析,引导学生深入探究函数模型的应用领域。
七、教学反思函数模型是数学中一个重要的概念,也是高中数学的核心内容之一、教师在教学中要注重培养学生的数学思维能力和应用能力,通过合理设计的学习任务,激发学生的兴趣,引导学生主动探索,提高学生对数学的理解和应用能力。




2019-2020学年(浙江专版)高考数学一轮复习(回扣主干知识+提升学科素养)第八章第七节抛物线教案文
【考纲下载】
1.掌握抛物线的定义、几何图形、标准方程及简单性质(范围、对称性、顶点、离心率等).
2.了解圆锥曲线的简单应用.了解抛物线的实际背景,了解抛物线在刻画现实世界和解决实际问题中的作用.
3.理解数形结合思想.
1.抛物线的定义
满足以下三个条件的点的轨迹是抛物线:
(1)在平面内;
(2)动点到定点F的距离与到定直线l的距离相等;
(3)定点不在定直线上.
(0,0)
1.当定点F在定直线l上时,动点的轨迹是什么图形?
提示:当定点F在定直线l上时,动点的轨迹是过定点F且与直线l垂直的直线.2.抛物线y2=2px(p>0)上任意一点M(x0,y0)到焦点F的距离与点M的横坐标x0有何关系?若抛物线方程为x2=2py(p>0),结果如何?
提示:由抛物线定义得|MF |=x 0+p
2;若抛物线方程为x 2
=2py (p >0),则|MF |=y 0+p
2
.
1.设抛物线的顶点在原点,准线方程为x =-2,则抛物线的方程是( )
A .y 2=-8x
B .y 2
=-4x
C .y 2=8x
D .y 2
=4x
解析:选C 由抛物线准线方程为x =-2知p =4,且开口向右,故抛物线方程为y 2
=8x .
2.抛物线y 2
=4x 的焦点F 到准线l 的距离为( ) A .1 B .2 C .3 D .4
解析:选B 因为抛物线y 2
=4x ,所以2p =4,而焦点F 到准线l 的距离为p =2.
3.抛物线y =2x 2
的焦点坐标为( ) A.⎝ ⎛⎭⎪⎫12,0 B .(1,0) C.⎝ ⎛⎭⎪⎫0,18 D.⎝ ⎛⎭
⎪⎫0,14 解析:选C 将抛物线y =2x 2化成标准方程为x 2=12y ,所以2p =12,p 2=18
,而抛物线x
2
=12y 的焦点在y 轴的非负半轴上,所以焦点坐标为⎝ ⎛⎭⎪⎫0,18. 4.抛物线的焦点为椭圆x 29+y 2
4
=1的左焦点,顶点为椭圆中心,则抛物线方程为
________________.
解析:由c 2
=9-4=5,得F (-5,0),
则抛物线方程为y 2
=-45x .
答案:y 2
=-45x
5.设抛物线y 2
=2px (p >0)的焦点为F ,点A (0,2).若线段FA 的中点B 在抛物线上,则B 到该抛物线准线的距离为________.
解析:F ⎝ ⎛⎭⎪⎫p 2,0,则B ⎝ ⎛⎭
⎪⎫p
4,1, ∴2p ×p
4=1,解得p = 2. ∴B ⎝
⎛⎭
⎪⎫
24,1, 因此B 到该抛物线的准线的距离为24+22=32
4
. 答案:32
4
前沿热点(十二)
与抛物线有关的交汇问题
1.抛物线是一种重要的圆锥曲线,在高考中,经常以抛物线为载体与直线、圆综合考查,主要考查抛物线的方程及几何性质,直线与抛物线的综合应用,点到直线的距离等.
2.直线与抛物线的综合问题,经常是将直线方程与抛物线方程联立,消去x (或y ),利用方程的根与系数的关系求解,但一定要注意直线与抛物线相交的条件.
[典例] (2013·浙江高考) 已知抛物线C 的顶点为O (0,0),焦点为F (0,1).
(1)求抛物线C 的方程;
(2)过点F 作直线交抛物线C 于A ,B 两点.若直线AO ,BO 分别交直线l :y =x -2于M ,N 两点,求|MN |的最小值.
[解题指导] (1)由抛物线的顶点、焦点即可判断抛物线的形状、大小,从而可求抛物线方程.
(2)直线AB 与抛物线相交,可得出A ,B 两点坐标之间的关系,再由AO 、BO 与直线l 交于M ,N 两点,可求出|MN |的表达式,用k 来表示,利用函数即可求最值.
[解] (1)由题意可设抛物线C 的方程为x 2
=2py (p >0),则p
2
=1,p =2,
所以抛物线C 的方程为x 2
=4y .
(2)设A (x 1,y 1),B (x 2,y 2),直线AB 的方程为y =kx +1. 由⎩
⎪⎨⎪⎧
y =kx +1,x 2=4y ,消去y ,整理得x 2-4kx -4=0, 所以x 1+x 2=4k ,x 1x 2=-4.
从而|x 1-x 2|=4k 2
+1.
由⎩⎪⎨⎪⎧
y =y 1x 1
x ,
y =x -2,
解得点M 的横坐标x M =2x 1x 1-y 1=2x 1x 1-
x 214
=8
4-x 1
. 同理点N 的横坐标x N =8
4-x 2.
所以|MN |=2|x M -x N |
=2⎪⎪⎪⎪
⎪
⎪84-x 1-84-x 2 =82⎪⎪⎪⎪⎪
⎪x 1-x 2x 1x 2-x 1+x 2+16
=8 2 k 2
+1|4k -3|
.
令4k -3=t ,t ≠0,则k =t +3
4
.
当t >0时, |MN |=2 2 25
t
2
+6
t
+1>22;
当t <0时, |MN |=2 2
⎝ ⎛⎭
⎪⎫5t +352+1625≥85 2. 综上所述,当t =-253,即k =-43时,|MN |的最小值是8
5
2.
[名师点评] 解答本题的关键有以下几点:
(1)由顶点O (0,0),焦点F (0,1)确定抛物线的开口方向及P 的值; (2)|MN |的表达式中,注意x 1+x 2,x 1x 2及|x 1-x 2|的值; (3)注意4k -3=t 的换元,使问题简单.
(2014·湖州模拟)已知抛物线C :y 2
=2px 的焦点为F ,抛物线C 与直线l 1:y =-x 的一个交点的横坐标为8.
(1)求抛物线C 的方程;
(2)不过原点的直线l 2与l 1垂直,且与抛物线交于不同的两点A ,B ,若线段AB 的中点为P ,且|OP |=|PB |,求△FAB 的面积.
解:(1)由题意知交点坐标为(8,-8),∴82=2p ×8,∴2p =8,所以抛物线方程为y 2
=8x .
(2)∵l 1:y =-x ,又直线l 2与l 1垂直,
所以可设l 2:x =y +m ,A (x 1,y 1),B (x 2,y 2),且直线l 2与x 轴交点为M .
由⎩
⎪⎨
⎪⎧
y 2
=8x ,x =y +m 得y 2
-8y -8m =0,
Δ=64+32m >0,∴m >-2.
由韦达定理,y 1+y 2=8,y 1y 2=-8m , ∴x 1x 2=
y 1y 2
2
64
=m 2
.
由题意可知OA ⊥OB ,即x 1x 2+y 1y 2=m 2
-8m =0, ∴m =8或m =0(舍), ∴l 2:x =y +8,M (8,0),
故S △FAB =S △FMB +S △FMA =1
2·|FM |·|y 1-y 2|
=3y 1+y 2
2
-4y 1y 2=24 5.。