全微分和热力学
- 格式:doc
- 大小:994.49 KB
- 文档页数:18

热力学一般关系本章提要及安排本章提要:1.工质的平衡热力性质是指工质状态参数间的函数关系,特别以可测参数为独立变量的热力学能、焓、熵函数在工程应用中尤为重要。
2.对热力学状态函数的研究通常从它们的偏微商着手。
在常用状态函数的偏微商中,有的是可以通过实验测定的,常将它们定义为各种热系数;有的则不能用实验的方法得出。
3.工质在准平衡变化中的热力学基本定律表达式同时也表达了热力学状态函数之间的基本关系,又称基本热力学关系式。
通过勒让德变换,基本热力学关系可以用不同的组合参数表达。
基本热力学关系的一阶偏微商和二阶混合偏微商给出状态函数偏微商之间的一般关系。
当然,与热力学基本定律一样这些一般关系对任何工质都是适用的。
4.按照基本热力学关系,可以用可测的状态参数和热系数来表达不能通过实验直接得出的偏微商,从而将各常用状态函数的全微分式用可测的参数及免系数表达出来。
这样,就为在实验测定数据的基础上得出工质的状态函数开辟了道路。
5.在工质热力性质研究中,并非所有热系数都是必需沤过实验测定的,应用热系数间的一般关系可以由少虽测得的热系数得到所需的其它热系数。
这样,可以大大减少研究中的实验工作量.同时减小由于有限的实验精确度带来的误差。
6.依据本章所导出的一般关系式,应用所讲述的推导方法,还可导得工程中需用的各种函数关系。
7.本章所导出的一般关系式只适用于简单可压缩系统。
本章要求:1.了解热力学一般关系的内容及其在工质热力性质研究中的地位和作用;2.掌握导出热力学一般关系的思路和推导方法;3.熟悉简单可压缩工质基本的和常用的热力学一般关系。
学习建议:本章学习时间建议共2学时:1.常用状态函数的偏微商;基本热力学关系; 1学时2.热力学能、焓和熵的微分式;热系数之间的一般关系; 1学时4.1 常用状态函数的偏微商本节知识点:状态方程的偏微商热力学能函数的偏微商焓函数的偏微商熵函数的偏微商本节参考图片:麦克斯韦汤姆逊汤姆逊实验本节疑问解答:思考题4.1.1 思考题4.1.2 思考题4.1.3本节基本概念:定温压缩系数压力的温度系数绝热压缩系数比定容热容比定压热容绝热节流系数工程中常用的状态函数有状态方程 F(p ,v ,T )=0,和以可测参数为独立变量的热力学能、焓、熵函数,通常热力学能函数u(T ,v ),焓函数h(T ,p),和熵函数s(T ,v),s(T ,p)的导得较为方便。

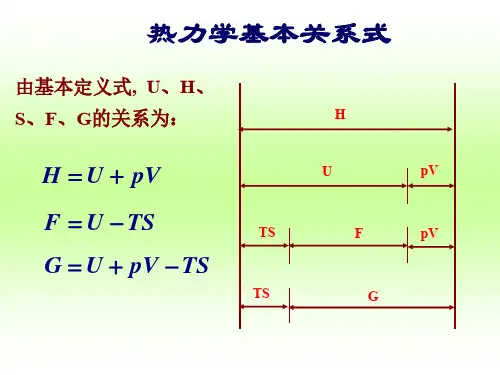





多元复相系的热力学函数U、H、F和G的全微分方程多元复相系的热力学函数U、H、F和G是描述系统热力学性质的重要量。
它们各自的全微分方程可以帮助我们更好地理解系统的变化和性质。
在本文中,我们将介绍这些热力学函数的全微分方程,以便更好地探讨多元复相系的性质。
这些方程是研究系统热力学性质的基础,通过对它们的分析,我们可以更深入地了解系统的特性和行为。
由于涉及到系统的热力学性质,这些全微分方程对于研究和理解多元复相系的行为具有重要的意义。
我们将在接下来的内容中详细介绍这些方程,以期帮助读者更好地理解多元复相系的热力学性质。
多元复相系指的是由两个或多个相组成的系统。
相在这里是指物质的不同物态形式,如固体、液体和气体。
在多元复相系中,相与相之间可以发生相变的过程,也就是物质从一个相态转变为另一个相态的过程。
这种相变可以是固液相变,也可以是液气相变或固气相变等。
在多元复相系中,各相之间可能存在平衡态或非平衡态。
平衡态指的是各相之间达到了稳定的相对平衡状态,没有进一步的相变。
非平衡态则表示相之间仍然存在着某种程度的不平衡,可能会继续发生相变。
多元复相系的研究对于理解物质的性质和相变规律非常重要。
通过研究不同相的组成、结构和特性,我们可以深入了解物质的行为和性质。
在实际应用中,多元复相系的研究也有着广泛的应用,例如在材料科学、化学工程和能源领域等。
通过控制相变过程,我们可以设计和制造具有特定性能的材料,提高能源利用效率,甚至开发新的材料和技术。
多元复相系是由两个或多个相组成的系统,其中相与相之间可以发生相变的过程。
在这些相变中,可能存在平衡态或非平衡态。
通过研究多元复相系,我们可以深入了解物质的性质和相变规律,并将其应用于实际生产和科学研究中。
热力学函数U是内能,它是系统的基本热力学性质之一。
U与系统的温度、体积和物质的性质有关。
U的全微分方程可以表示为:dU = TdS - PdV + ΣμidNi其中T是系统的温度,S是系统的熵,P是系统的压强,V是系统的体积,μi是组分i的化学势,Ni是组分i的摩尔数。

§内能、焓、自由能和吉布斯函数的全微分热力学函数中的物态方程、内能和熵是基本热力学函数,不仅因为它们对应热力学状态描述第零定律、第一定律和第二定律,而且其它热力学函数也可以由这三个基本热力学函数导出。
焓:自由能:吉布斯函数:下面我们由热力学的基本方程(1)即内能的全微分表达式推导焓、自由能和吉布斯函数的全微分焓、自由能和吉布斯函数的全微分o焓的全微分由焓的定义式,求微分,得,将(1)式代入上式得(2)o自由能的全微分由得(3)o吉布斯函数的全微分(4)从方程(1)(2)(3)(4)我们容易写出内能、焓、自由能和吉布斯函数的全微分dU,dH,dF,和dG独立变量分别是S,V;S,P;T,V和T,P所以函数U(S,V),H(S,P),F(T,V),G(T,P)就是我们在§将要讲到的特性函数。
下面从这几个函数和它们的全微分方程来推出麦氏关系。
二、热力学(Maxwell)关系(麦克斯韦或麦氏)(1)U(S,V)利用全微分性质(5)用(1)式相比得(6)再利用求偏导数的次序可以交换的性质,即(6)式得(7)(2)H(S,P)同(2)式相比有由得(8)(3)F(T,V)同(3)式相比(9)(4)G(T,P)同(4)式相比有(10)(7),(8),(9),(10)式给出了热力学量的偏导数之间的关系,称为麦克斯韦()关系,简称麦氏关系。
它是热力学参量偏导数之间的关系,利用麦氏关系,可以从以知的热力学量推导出系统的全部热力学量,可以将不能直接测量的物理量表示出来。
例如,只要知道物态方程,就可以利用(9),(10)式求出熵的变化,即可求出熵函数。
§麦氏关系的简单应用证明1. 求选T,V为独立变量,则内能U(T,V)的全微分为(1)熵函数S(T,V)的全微分为( 2)又有热力学基本方程(3)由(2)代入(3)式得(4)(4)相比可得(5)(6)由定容热容量的定义得(7)2. 求选T 、P为独立参量,焓的全微分为(8)焓的全微分方程为(9)以T、P为自变量时熵S(T、P)的全微分表达式为(10)将(10)代入(9)得(11) (8)式和(11)式相比较得(12)(13)(14)3求由(7) (14)式得(15)把熵S看作T,V的函数,再把V看成T,P的函数,即对上式求全微分得∴代入(15)式得由麦氏关系得(16)即得证4、P,V,T三个变量之间存在偏导数关系而可证(17)§气体的节流过程和绝热膨胀过程气体的节流过程(节流膨胀)和绝热膨胀是获得低温的两种常用方法,我们利用热力学函数来分析这两种过程的性质一,气体的节流(焦耳---汤姆逊效应)1、定义:如图所示有一由绝热材料制成的管子,中间用一多孔塞(节流阀)隔开,塞子一边维持较高的压强P,另一边维持较低的压强P,在压力的作用下,气体由高压的一边经过多孔塞流向低压的一边。

热力学第一定律 公式 解释 备注1V V U T T U U TV d d d ⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=系统的热力学能U 可看做温度T 和体积V 的函数,可写作全微分。
热力学能是状态性质,故用U d 以表示它是全微分。
2(微分式)W Q U δδ+=d (积分式)W Q U +=∆ 系统的热力学能变化量U ∆等于系统与环境交换的热Q 和功W 之和。
热和功不是状态性质,故用Q δ和W δ而不是Q d 和W d 以表示它们不是全微分。
规定,系统得到热或得到功时Q 和W 为正,反之系统失去热或对外做功时Q 和W 为负。
3 (微分式)外V p W d -=δ 体积功等于气体膨胀或压缩时抵抗外压所做的功。
负号是因为规定系统对外做功时W 为负。
推导:气体抵抗外压外p 膨胀,使得截面积为A 的理想活塞移动了l d ,可以求出膨胀所做的功为dV p Adl p dl F W 外外外-=-=-=δ。
(向真空膨胀)0=W(恒外压膨胀)外V p W ∆-=(定温定压可逆相变)V p W ∆-= (理气等温可逆膨胀)⎪⎪⎭⎫⎝⎛-=12V V nRT W ln推导:向真空膨胀,0=外p 。
等温可逆膨胀时,内压p 恒比外压外p 大p d ,()⎰⎰--=-=2121d d d V V V V V p p V p W 外,忽略二阶小量V p d d ,并将理想气体方程V nRT p =带入得⎪⎪⎭⎫ ⎝⎛-=-=⎰1221d V V nRT V V nRTW VV ln 。
4 U Q V ∆=恒容过程的热等于热力学能变。
V Q 是状态函数。
推导:V p Q W Q U d d -=+=δδδ,定容条件下0d =V ,可得U Q V d =δ,积分后即为U Q V ∆=5H Q P ∆=恒压过程的热等于焓变。
p Q 也是状态函数。
推导:V p Q W Q U d d -=+=δδδ,定压条件下(21p p =)积分,可得()()H H H V p U V p U V p U Q p ∆=-=+-+=∆+∆=12111222,其中焓H 被定义为pV U H def+==。
Univ. Chem. 2023, 38 (11), 309–316 309收稿:2023-03-28;录用:2023-05-18;网络发表:2023-05-31 *通讯作者,Email:***************.cn基金资助:中央高校基本科研业务费(2652019111)•自学之友•doi: 10.3866/PKU.DXHX202303086基于全微分方程探讨关于熵的热力学关系式杨德重*中国地质大学(北京)数理学院,北京 100083摘要:在教学过程中,以熵的全微分方程为基点,将热力学第一定律和热力学第二定律的相关知识串联,形成了基于熵的热力学关系式网络,有助于学生对相关知识的学习和运用。
关键词:热力学;熵;全微分;理想气体 中图分类号:G64;O6Discussion of Thermodynamic Equations about Entropy Based on Total DifferentialsDezhong Yang *School of Science, China University of Geosciences, Beijing 100083, China.Abstract: Throughout the teaching process, we established connections between the first and second laws of thermodynamics, centering on the concept of entropy’s total differentials. This approach creates a cohesive network of thermodynamic equations, fundamentally grounded in the concept of entropy. By linking these concepts, we aim to facilitate students’ understanding and application of these essential thermodynamic principles.Key Words: Thermodynamic; Entropy; Total differentials; Ideal gases熵是热力学第二定律的核心概念,学习和理解熵的概念对于掌握热力学第二定律起着关键的作用[1,2]。
热力学基础中的热力学过程与全微分的推导热力学是研究物质之间能量转化和传递规律的科学,而热力学过程则是描述物质在状态变化过程中所遵循的规律。
在热力学过程中,通过将能量转化为热和功,物质的性质和状态会发生变化。
本文将介绍热力学过程的概念以及全微分的推导。
一、热力学过程的概念热力学过程是指当一个系统与外界发生能量和物质的交换时,系统的热力学性质发生变化的过程。
热力学过程可以分为准静态过程和非准静态过程两种。
准静态过程是指系统的热力学状态变化十分缓慢且无限接近于平衡态的过程。
在准静态过程中,系统的所有性质都可以被看作是均匀的,且系统与外界之间存在连续的热和功交换。
非准静态过程则是指系统状态的变化过程快于系统达到平衡的速度。
在非准静态过程中,系统与外界之间的热和功交换会出现不可逆过程,系统的各项性质难以均匀分布。
二、全微分的推导全微分是热力学过程中描述系统状态变化的工具之一。
全微分可以理解为描述系统各个状态量(如温度、压力、体积等)之间微小变化关系的差分。
对于热力学过程中的状态函数而言,其变化可以用全微分来表示。
在热力学中,最常用的全微分表达式是对内能的全微分形式,即dU = TdS - PdV。
其中,dU表示内能的微小变化量,T表示温度,S表示熵,P表示压强,V表示体积。
这个全微分的推导可以通过将系统的能量变化表示为总热量和总功之和来得到。
根据热力学第一定律,系统的内能变化等于吸热减去做功,即dU = Q - W。
接下来,将吸热表示为温度和熵的乘积,即Q = TdS,将做功表示为压强和体积的乘积,即W = -PdV。
将Q和W代入dU的表达式中,得到dU = TdS - PdV。
这个全微分表达式说明了内能变化的量完全由温度、熵、压强和体积的微小变化引起。
通过对这些微小变化进行积分,可以得到系统在整个过程中的内能变化量。
三、热力学过程中的应用热力学过程中的全微分推导对于分析和描述各种过程具有重要的应用意义。
热力学基础中的热力学过程与全微分的计算在热力学基础中,热力学过程是指热力学系统从一个状态转化为另一个状态的过程。
而全微分是用来计算热力学系统在不同状态下发生的过程中的能量变化的方法。
本文将探讨热力学过程与全微分的计算方法。
一、热力学过程的概念与分类热力学过程是指热力学系统从一个平衡态转变为另一个平衡态的过程。
根据热力学系统的特性以及过程的特点,热力学过程可以分为四类:等温过程、绝热过程、等容过程和等压过程。
1. 等温过程:在等温过程中,系统的温度保持不变,即系统与外界保持热平衡。
在这种过程中,系统与外界之间发生的能量转化主要是热量和功。
根据热力学的第一定律,等温过程中系统的内能不变,即ΔU=0。
2. 绝热过程:在绝热过程中,系统与外界之间不进行热量的交换,即系统与外界之间没有热流动。
在这种过程中,系统与外界之间发生的能量转化主要是功。
根据热力学的第一定律,绝热过程中系统的内能变化仅由功所做的功决定,即ΔU=W。
3. 等容过程:在等容过程中,系统的体积保持不变,即系统与外界保持定容。
在这种过程中,系统与外界之间发生的能量转化主要是热量。
根据热力学的第一定律,等容过程中系统的内能变化仅由热量所做的功决定,即ΔU=Q。
4. 等压过程:在等压过程中,系统的压强保持不变,即系统与外界保持定压。
在这种过程中,系统与外界之间发生的能量转化主要是热量和功。
根据热力学的第一定律,等压过程中系统的内能变化由热量和功的和决定,即ΔU=Q-W。
二、全微分的计算方法在热力学中,全微分用来描述系统的微观状态变化时,系统内部各个性质的微小变化。
全微分可以表示为以下形式:dU = δQ - δW。
其中,dU表示系统内能的变化量,δQ表示系统所吸收或释放的热量,δW表示系统所做的功。
具体计算全微分的方法根据不同的热力学过程有所不同。
1. 等温过程中的全微分计算:在等温过程中,系统的温度保持不变,即ΔT=0。
根据热力学的第一定律,等温过程中系统的内能不变,即ΔU=0。
2014届本科毕业论文全微分与热力学姓名:高盼系别:物理与电气信息学院专业:物理学学号:100314015指导教师:王保玉2014年2月9日目录摘要与关键字 (II)0 引言....................................................... 错误!未定义书签。
1 全微分函数的基本性质....................................... 错误!未定义书签。
2 热力学基本方程及辅助热力学方程 (3)2.1 物态方程 (3)2.2 态函数内能U和熵S (4)2.3 热力学基本微分方程 (5)3 内能、焓、自由能及吉布斯函数的全微分和麦克斯韦关系 (5)4 麦克斯韦关系的简单应用 (7)4.1 熵的一般关系式 (7)4.2 内能的一般关系式 (9)4.3 焓的一般关系式 (10)4.4 定压比热与定容比热的关系 (13)摘要 (II)关键词 (II)参考文献 (14)致谢 (15)全微分与热力学摘要基本热力学状态函数及其辅助函数许多都是不可测量,必须将它们与可测量联系起来才便于确定,但数学推导过于复杂。
本文从四个热力学基本方程出发, 利用函数全微分性质,对比研究可得出八个对应系数关系式,再对其二次微分得出四个麦克斯韦关系式,方便对热力学系统进行研究。
关键词热力学基本方程;全微分;麦克斯韦关系;不可测量;可测量;热力学系统Total differential and thermodynamicsAbstractMany basic thermodynamic state function and the auxiliary function are measured, they must be linked with measurable just easy to determine, but the mathematical deduction is too complex.In this paper, in four fundamental equations of thermodynamics, the total differential properties, functions comparative study can be concluded that eight corresponding coefficient relation, again the second time differential draw four maxwell's equation, is convenient to study thermodynamics system.Key wordsThe thermodynamic basic equations; Total differential; Maxwell relations; Immeasurability; Measurability; Thermodynamic system0 引言热力学是研究热能与其他形式能量的转换规律的科学,着重阐述工质的热力学性质、基本热力过程以及热工转换规律,最终找出提高能量利用效率的方法,从而促进为人类文明的进步。
[1]热力学函数全微分关系式的推证,是要把热力学体系不易测量的热力学函数的全微分用实验易于测量的物理量如P 、V 、T 、S 、等温膨胀系数、等温压缩系数、等体热容、等压热容等表示出来,这样就可以研究热力学系统求解实际问题了,如工质的性质、最大功的计算等。
[2]在这方面已有许多教材和报告给出证明,但是其中的数学推导步骤过于复杂,对于初学者来说很难接受。
我作为一个学生,站在学生的角度,在在不失科学性的前提下,用尽量简单的数理知识总结出“四-八-四”关系式,通过此式,同学们不仅轻松接受,而且对热力学基本方程及其完整的微分性质有更加清晰的理解。
此外熵、内能和焓的一般关系式中均含有定压比热或者定容比热,定压比热的测定较易,因此我们要设法找到两个比热的关系,从而由定压比热计算出定容比热,以避开实验测定定容比热的困难,最后根据利用“四-八-四”关系式导出基本热力学函数,就可以对热力学系统进行研究了。
1全微分函数的基本性质设函数(,)z f x y =在点(,)x y 的某邻域内有定义,如果函数在点(,)x y 的全增量z (,)(,)f x x y y f x y ∆=+∆+∆- 可以表示为 z ()A x B y O ρ∆=∆+∆+其中A 、B 不依赖于y x ∆∆、而仅与y x 、有关,则称函数(,)z f x y =在点(,)x y 可微分,而x A B y ∆+∆称为函数(,)z f x y =在点(,)x y 的全微分,记作dz 即z y x z z d dx dy x y ⎛⎫∂∂⎛⎫=+ ⎪ ⎪∂∂⎝⎭⎝⎭[3]状态函数的全微分性质状态参数,当我们强调它们与独立变量的函数关系时,常称它们为状态函数。
从数学上说,状态函数必定具有全微分性质。
这一数学特性十分重要,利用它可导出一系列很有实用价值的热力学关系式。
下面我们扼要介绍全微分的一些基本定理。
[4]设函数),(y x f z=具有全微分性质z y xz z d dx dy x y ⎛⎫∂∂⎛⎫=+ ⎪ ⎪∂∂⎝⎭⎝⎭ (1) 则必然有(1) 互易关系令式(1)中()1,y z f x y x ∂⎛⎫=⎪∂⎝⎭, ()2,xz f x y y ⎛⎫∂= ⎪∂⎝⎭则 12y x f f y x ⎛⎫∂∂⎛⎫=⎪ ⎪∂∂⎝⎭⎝⎭ (2)互易关系与⎰=0dz 等价。
它不仅是全微分的必要条件,而且是充分条件。
因此,可反过来检验某一物理量是否具有全微分。
(2) 循环关系当保持z 不变,即0=dz 时,由式(1),得0=⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫⎝⎛∂∂z xz y dy y z dx x z 则 xy zy z x z x y ⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂1z yx z y x y x z ⎛⎫∂∂∂⎛⎫⎛⎫=-⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭(3) 此式的功能是:若能直接求得两个偏导数,便可确定第三个偏导数。
结果也很容易记忆,只需将三个变量依上、下、外次序,即))()((xzy yxz zyx 循环就行了。
(3) 变换关系将式(1)用于某第四个变量ω不变的情况,可有ωωωdy y z dx x z dz xy ⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫⎝⎛∂∂= 两边同除以ωdx ,得y x z z z y x x y x ωω⎛⎫∂∂∂∂⎛⎫⎛⎫⎛⎫=+ ⎪⎪ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭ (4)式中:y x z ⎪⎭⎫ ⎝⎛∂∂是函数),(y x z 对x 的偏导数;ω⎪⎭⎫ ⎝⎛∂∂x z 是以),(ωx 为独立变量时,函数),(ωx z 对x 的偏导数。
上面的关系可用于它们之间的变换。
(4) 链式关系按照函数求导法则,可有下述关系:1=⎪⎭⎫⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂yy z x x z (5)1y y yz x x z ωω∂∂∂⎛⎫⎛⎫⎛⎫=⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭(6) 这是在同一参数(如y )保持不变时,一些参数),,,( ωx z 循环求导所得偏导数间的关系。
若将关系式中每个偏导数视为链的一环,则链式关系的环数可随所涉及参数的个数而增减。
2 热力学基本方程及辅助热力学方程2.1物态方程在介绍具体物质的物态方程前,先介绍几个与物态方程有关的物理量体胀系数(压强保持不变的情况下,温度升高1K 所引起的物体体积的相对变化)1P V V T α∂⎛⎫=⎪∂⎝⎭压强系数(体积保持不变的情况下,温度升高1K 所引起的物体压强的相对变化)1V p p T β∂⎛⎫=⎪∂⎝⎭等温压缩系数(温度保持不变情况下增加单位压强所引起的物体体积的相对变化)1T T V V P κ∂⎛⎫=- ⎪∂⎝⎭[3]由微分性质循环关系式(3)得1T V PV P T P T V ∂∂∂⎛⎫⎛⎫⎛⎫=- ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭ (7)因此 T Pακβ= 三者之间可以转换(1)理想气体的物态方程PV nRT = (8) (2)简单固体和液体由于固体和液体的膨胀系数是温度的函数,与压强近似无关,等温压缩系数可以近似看作常量,因为 (,,)0f p V T = (,)V V p T = p TV V dV dp dT p T ⎛⎫∂∂⎛⎫=+ ⎪ ⎪∂∂⎝⎭⎝⎭11T pT dV V V dp dT dp dT V V p V T κα⎛⎫∂∂⎛⎫=+=-+ ⎪ ⎪∂∂⎝⎭⎝⎭两端积分得000Vp T T V p T dV dp dT V κα=-+⎰⎰⎰ 00(p p )(0T T T V V e κα--+-=) 00(p p )()000,)(T ,)T T T V T p V p e κα--+-=( 令00p =00(p p )()00,)(T ,0)T T T V T p V e κα--+-=( 利用泰勒公式展开得000(,)(,0)[1()]T V T P V T TT p ακ=+-- (9)(3)顺磁性固体(,,)0f M H T = H 表示磁场强度 M 表示磁化强度 T 表示温度实验测得一些物质的磁物态方程为 CM HT =(10)(C 为常数,其值因物质的不同而异)此式又称为居里定律。
[5]2.2态函数内能U 和熵S(1)内能:焦耳所做实验表明,系统经绝热过程从初态到末态,在此过程中外界对系统所作的功仅取决于系统的初、末态,而与过程无关,这个事实表明,可以用绝热过程中外接对系统所作的功S W 定义一个态函数U 在末态B 与初态A 之差B A SU U W -=如果系统经历的过程不是绝热过程,初、末态的内能变化等于外接对气体做的功与从外界吸收的热量之和,即:B A U U W Q-=+ (11)其微分形式是:dU dQ dW =+ (12)(2)熵函数:对于可逆过程有0dQT =⎰,dQ 为系统从温度为T 的热源所吸收的热量。
设想系统从初始状态A 经过可逆过程1到达终态B 后,又经过另一可逆过程2回到初始状态A ,这两个过程构成一个循环过程,根据上式 有 120BAA B dQ dQ T T +=⎰⎰由于1、2是由A 态到B 态的两个任意过程,上式表明,在初始状态A 和终态B 给定后积分BA dQ T ⎰与可逆过程的路径无关。
克劳修斯根据此性质引入一个态函数:BA B AdQS S T -=⎰ 对上式取微分得dQdS T =(13)此式表明在无穷小的可逆过程中,系统的熵变ds 与其温度T 及其在过程中吸取的热量dQ 的关系。