2第二章_热力学函数与普遍关系式
- 格式:doc
- 大小:1.47 MB
- 文档页数:28










第二章 热力学第二定律 一、基本公式和基本概念 基本公式1. 热力学第二定律的数学表达式----克劳修斯不等式 ()0A B A B QS Tδ→→∆-≥∑2. 熵函数的定义 ()R QdS Tδ=, ln S k =Ω3. 熵变的计算理想气体单纯,,p V T 变化22,1122,1122,,11ln ln ln ln lnln V m p m p m V m T V S C R T V T p S C R T p V p S C C V p ∆=+∆=-∆=+理想气体定温定压混合过程ln i i iS R n x ∆=-∑封闭系统的定压过程21,d T p m T C S n T T∆=⎰封闭系统定容过程 21,d T V m T C S n T T∆=⎰可逆相变 m n H S T∆∆=标准状态下的化学反应 ,()r m Bm B BS S T θθν∆=∑定压下由1T 温度下的化学反应熵变求2T 温度下的熵变 21,21()()d T p m r m r m T C S T S T T T∆∆=∆+⎰4. 亥姆霍兹函数 A U TS ≡-5. 吉布斯函数 G H TS ≡-6. G ∆和A ∆的计算(A ∆的计算原则与G ∆相同,做相应的变换即可)定温过程G H T S ∆=∆-∆组成不变的均相封闭系统的定温过程 21d p p G V p ∆=⎰理想气体定温过程 21ln p G nRT p ∆= 7. 热力学判据熵判据:,()0U V dS ≥亥姆霍兹函数判据:,,'0(d )0T V W A =≤ 吉布斯函数判据:,,'0(d )0T p W G =≤8. 热力学函数之间的关系组成不变,不做非体积功的封闭系统的基本方程d d d d d d d d d d d d U T S p V H T S V pA S T p V G S T V p=-=+=--=-+麦克斯韦关系S VpS T Vp TT p V S T V p S S p V T S V p T ∂∂⎛⎫⎛⎫=- ⎪ ⎪∂∂⎝⎭⎝⎭⎛⎫∂∂⎛⎫= ⎪ ⎪∂∂⎝⎭⎝⎭∂∂⎛⎫⎛⎫= ⎪ ⎪∂∂⎝⎭⎝⎭⎛⎫∂∂⎛⎫=- ⎪ ⎪∂∂⎝⎭⎝⎭9. 吉布斯-亥姆霍兹方程2()pG HT T T ∆⎡⎤∂⎢⎥∆=-⎢⎥∂⎢⎥⎣⎦ 基本概念1. 热力学第二定律在研究化学或物理变化驱动力来源的过程中,人们注意到了热功交换的规律,抓住了事物的共性,提出了具有普遍意义的熵函数。
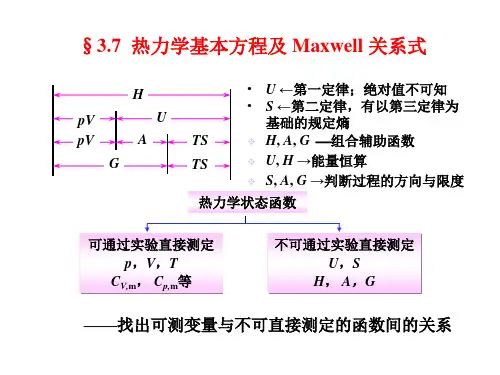
热力学一般关系(热学-高等数学-偏微分)第二部分工质的热力性质六热力学函数的一般关系式由热力学基本定律引出的一些基本热力学状态函数(如内能U、熵S)及其为某一研究方便而设的组合函数(如焓H、自由能F、自由焓G等)许多都是不可测量,必须将它们与可测量(如压力p、体积V、温度T等)联系起来,否则我们将得不到实际的结果,解决不了诸如上一章讲的最大功计算等一些具体的问题。
这就需要发展热力学的数学理论以将热力学基本定律应用到各种具体问题中去。
热力学函数一般关系式 全微分性质+基本热力学关系式6.1 状态函数的数学特性对于状态参数,当我们强调它们与独立变量的函数关系时,常称它们为状态函数。
从数学上说,状态函数必定具有全微分性质。
这一数学特性十分重要,利用它可导出一系列很有实用价值的热力学关系式。
下面我们扼要介绍全微分的一些基本定理。
设函数),(y x f z =具有全微分性质dy y z dx x z dz xy ⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫⎝⎛∂∂= (6-1) 则必然有(1) 互易关系令式(6-1)中),(y x M x z y=⎪⎪⎭⎫⎝⎛∂∂,),(y x N y z x=⎪⎪⎭⎫⎝⎛∂∂ 则 y xx N yM ⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫⎝⎛∂∂ (6-2)互易关系与⎰=0dz 等价。
它不仅是全微分的必要条件,而且是充分条件。
因此,可反过来检验某一物理量是否具有全微分。
(2) 循环关系当保持z 不变,即0=dz 时,由式(6-1),得0=⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫⎝⎛∂∂z xz y dy y z dx x z则 xy zy z x z x y ⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂ 故有 1-=⎪⎪⎭⎫⎝⎛∂∂⎪⎪⎭⎫⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂yz x z x x y y z (6-3)此式的功能是:若能直接求得两个偏导数,便可确定第三个偏导数。
结果也很容易记忆,只需将三个变量依上、下、外次序,即))()((xzy yxz zyx 循环就行了。
第二章 热力学函数与普遍关系式在给出了热力系统的一段性描述之后,就可以根据热力学第一定律和第二定律建立的解桥式,推导出热力学参数的各种微分关系式。
这种推导过程只应用连续可微函数的数学性质,而不涉及系统的特殊情况,因此它们适用于状态连续变化的一切系统以及系统的全部状态,通常称之为热力学普遍关系式。
热力学普遍关系式是非常有用的,利用有关的式子,可以由可测量决定非可测量,或对实例量进行热力学一致性检验。
此外不论如何严密与细致的实验,所切得的数据总是有限的,在编制参数图表时,必须进行内插与外推,这时普遍关系式是导出有关公式的重要依据。
2-1 热力学一般关系式1 一般关系式热力学的普遍关系式热力学一般关系据热力学基本定律导出,因此是任何工质都必然遵循的关系;是研究工质热力性质的理论基础,适于主要对象有约束作用的复杂系统对复杂系统的热力学分析。
热力学分析的主要对象的限制包括以下几点:● 化学成分均匀不变 ● 纯物质● 不存在运动、毛细、固体变形效应● 不存在电场、磁场效应,忽略重力效应。
简单可压缩系统一种与外界只有热量及准静态容积变化的热力学系统,其中:简单表示只有一种可逆功方式、可压缩表示可逆过程中,以体积变化做功,p d v 确定系统状态所需的参数:热力学关系式中参数的个数是确定的,它们与能量相互作用方式数有相关关系。
一个系统平衡状态所需的独立参数个数,等于可能存在的可逆功方式数再加一。
其中,加一是因为系统中的热作用。
两参数法则:一个简单系统平衡状态可由二个独立状态参数表示,同时二个独立状态参数也确定了一个简单系统平衡状态,即简单系统平衡状态 2独立状态参数 [例] U ,V 非相互独立。
D ,M 非相互独立。
纯物质:液体 + 蒸汽混合物, T, P 非相互独立热力学普遍关系式的功能:●由可测参数及其它参数,计算不可测参数●使计算简化●对实测量进行热力学的一致性校验●数据的内插及外插,(由实测数制表时)2 热力学特征函数热力学特征函数所谓热力学特征函数是指由自然的或适当的独立变量对(对非简单系统则为独立变量组)所构成的一些显函数它们能够全面而确定地描述热力系统的平衡状态。
就工程热力学的范畴来说,在一定条件下这些函数都有明确的物理意义,在数学上具有连续可微函数的一切特性。
总结一下,热力学特征函数有以下特点●适当的独立变量,构成显函数,全面、确定的描述系统平衡态●有明确的物理意义●连续、可微的函数热力学普遍微分关系的主要依据:●特征函数,以及偏函数●Maxwell关系由热力学第一、二定律结合而获得的以自然独立变量熵S、体积V表示的内能U(S,V)就是一个特征函数,因为它包含了一个平衡系统所有的热力学信息。
由第一定律,有dS=dU+P dVT所以,dU=dS-P dVT是U的全微分一个作为特征函数的热力学函数的独立变量对的选择必须适当,不能是任意的。
例:例如,如选择T、V作独立变量并构成函数U(T, V),则所包含的信息就比U(S, V)少。
函数U(T, V)的确定:U=U(S, V)(,)(,)[][]V SU S V U S V dU dS dVS V∂∂⇒=+∂∂对比dU=dS-P dVT11(),1(),i m i my y X x i X x i mx x ∂∂=≠=≠∂∂ 有:(,)(,)(,){[]}(,)[]V VU U S V U S V U T V U V U S V S T S =⎧∂⎪⇒=∂⎨∂=⎪∂⎩, 为偏微分方程,积分式包含一任意的积分函数,所以不是特征函数。
那么,是否还有采用其他不同于S 、V 的独立变量的特征函数呢?回答是肯定的,问题是怎样把它们找出来。
最方便的办法是通过勒让德变换(Legendre transformation)。
1869年,马修(F. Massieu)首先特勒让德变换应用于热力学函数的变换,其要点可简述如下:其主要思想:替换独立变量→其它特征函数 设:有函数Y=Y(x 1,x 2,…x m ),x 1-x m 为独立变量, dy=X 1dx 1+X 2dx 2+…+X m dx m 其中: X 1,…X m 为x 1, x 2…x m 的函数引入函数Y 1=Y-X 1x 1 ∴ dY 1=dY-X 1dx 1-x 1dX 1 代入dY :dY 1=-x 1dX 1+X 2dx 2+…+X m dx m所以,Y 1为X 1,x 2,x 3…x m 作独立变量的新函数 其中,x 1非独立变量可证:Y 1函数与Y 函数有同样的信息量。
几何说明:曲线包络线的切线族⇒表示曲线——可逆转换 例: 12(,,,)m y y x x x =⋅⋅⋅,可表示为m+1度的空间点的轨迹,y 随着1x 的变换 ⇐ y -1x 平面上切线包络线令:1Y 表示1x 切线的截距11211(,,,)m Y X x x Y X x ⋅⋅⋅=-xy()y y x =1y y X x=-则 112(,,,)m y X x x ⋅⋅⋅⇒Y 对于x 的一阶Legendre 变换所以Legendre 变换产生一函数,其斜率代替一个或几个独立变量 例:若()Y Y x =则1Y Y Xx =-,切线斜率为X,切线截距为1Y 由此推论:,()j j i i x i y X x ≠∂=∂ ,()j j i i ix iY x X ≠∂=-∂两者有简单的互逆变换关系所以,要互换独立变量和非独立变量的位臵,可用()i i i i i i d X x X dx x dX =+即,()i i i i i i X dx d X x x dX -=- 由Y 1=Y-X 1x 1 或Y 1=Y+X 1x 1有dY 1=dy-d(X 1x 1) 或dY 1=dY+d(X 1x 1) 可知,Legendre Trans :()i iY dY d x x ∂±∂结果,x i →非独立变量,X i =iY x ∂∂ →独立变量,两者有负逆变换关系。
例,由U=U(S,V), 所以dU=Tds-pdv, T 即1Y x ∂∂有:dU-d(TS)=dF或:dF=-SdT-pdv 自由能,Helmholtz 函数 例:dU+d (pV)=dH ,焓,p 即2Y x ∂∂dH=TdS+vdp例:dU-d(TS)+d(pv)=dGdG=-SdT+Vdp 自由焓,吉布斯函数 都是特征函数,都与U 密切相关: 所以:F=U-TS H=U+pVG=U+pV-TS=H-TS焓F 、自由能G 、自由焓H 都和内能密切相关。
由于内能的绝对值无法测定,因此其他三个因数的绝对值也不能测定。
T=0时,设U 0=0 则:F 0=U 0H 0=U 0+pv ,因为T=0凝聚,pV →0,所以H 0=U 0 G 0=H 0=U 0温度为T 时:'0U U U =-'0H H H =- '0F F F =- '0G G G =- 在d d d U T S P V=-,,)U S V =(进行T 与S ,P 与V 的独立变量替换 ,,F H G ⇒(,),(,),(,),F F T V dF SdT P dVH H S P dH TdS V dP G G T P dG SdT V dP ==--==+==-+S T V P→→()V U TS∂=∂ ,即 1X TS 即11X x , U 即Y()()()[][][]V V V U TS U TS T S P V TS STTT∂-∂-∂∂-∂-∂===-∂∂∂即,()()dU TdS PdVdF dU d TS TdS d TS PdV SdT PdV=-=-=--=--或[相当于:()i i i i i i X dx d X x x dX -=-]H ’G ’U ’F ’同理,U V∂∂S()=-P , 即: ∂∂2S (U+PV )X :[]=V(-P )PV 即是22X x()()dH dU d pv TdS PdV d PV TdS VdP∴=+=-+=+以上两式全用:()()()()dG dU d TS d pv TdS d TS PdV d PV SdT VdP=-+=--+=-+原因,服从负逆变换关系:S v TF T v SU -=∂∂=∂∂)()(而(),[]()s s U H S V Vp ∂∂=--=∂∂-注意:T-S ,P-V 的负逆变换关系,不能交叉进行。
简单可压缩系统,独立变量为2,m=2 特征函数4,为2m广义功效p dv 为1, m-1=1所以,可选为自变量的参数函数为2m ,分配在m 对中,每对乘积X i dx i 都具有能量的量纲,可构成特征函数2m 个。
其它基本方程式: 由S=S(U 、V)出发。
由dV=TdS-pdv 化出:dv Tp du Tds +=1所以 1(),()S p S v vT UT V∂∂==∂∂进行Legendre Trans ,可得Massieu 函数和Plank 函数。
对(T )-(U ),(T )-(P )过程,作用如F ,G : 2-2 偏导数关系和Maxwell 关系 1 偏导数一般关系。
全微分:若,状态参数z 为另两个独立参数x ,y 的函数 z=z(x,y) 有 ()()y x z z dz dx dy xy∂∂=+∂∂或dz=Mdx+Ndy 则:()()M N z z x y yXy xxdy∂∂∂∂==∂∂∂∂∂即——dz=Mdx+Ndy 为全微分的充要条件Z ——点函数,dz ——恰当微分,⎰=2121),(z z f dz∮dy=0偏导数变量互换选择变量时应注意计算的方便,以只需互换选择变量基本要求。
若x 、y 、z 、α任两个可做简单系统的独立变量(,)x x y α=, ()()x y x x dx dy d yαα∂∂=+∂∂(,)y y z α=, ()()z y y dx dy d zααα∂∂=+∂∂后式代入前式()(){()()()}z y x y x y x dx dy d y zy αααααα∂∂∂∂∂=++∂∂∂∂∂(,)x x z α=令,()()z x x dx dz d z ααα∂∂=+∂∂有由此定义可知:),(),(),(),(),(),(x y A B y x A B y x B A ∂∂=∂∂-=∂∂,即反序原理。
(,zα应为独立变量),所以上两式应相等,()()()()z y z x x x y yαααα∂∂∂∂∴=+∂∂∂∂和()()()x x y zyzααα∂∂∂=∂∂∂ 或 ()()()1x y z yzxααα∂∂∂=∂∂∂ 链式关系链关系的环可增可减,()()()()1x y z y z x ααααββ∂∂∂∂=∂∂∂∂()()1y x x y αα∂∂=∂∂ 即 1()()y x xyαα∂=∂∂∂ 倒数关系仅涉及3个变量时,(,),(,)x x y z y y x z == 有()()z y x x dx dy dz y z∂∂=+∂∂和()()z x y y dy dx dzx z ∂∂=+∂∂把dy 代入dx 中, ()()()()()z z z x y x y x y x dx dx dz yxyzz∂∂∂∂∂=++∂∂∂∂∂对所有dx ,dy 都成立 当dx =0时,有:()()()1z x y x y z yzx∂∂∂=-∂∂∂ 循环关系Jacob 行列式令: ()()()()()()()()yx y x x yy x A Ax y A B A BB B x y y x x y ∂∂⎛⎫ ⎪∂∂∂∂∂∂⎪=-∂∂∂∂∂∂ ⎪ ⎪∂∂⎝⎭J=记为:(,)(,)A B J x y ∂=∂ 适合于任何偏导数由此定义可知:),(),(),(),(),(),(x y A B y x A B y x B A ∂∂=∂∂-=∂∂ 反序原理y y x x y xA xy yA y y xA y xB A )()()()()(),(),(∂∂=∂∂∂∂-∂∂∂∂=∂∂共有变量原理 可证),(),(1),(2),(B A y x y x B A ∂∂=∂ 倒数原理2 Maxwell 关系对于纯物质、简单、可压缩、闭口系统,有以下特征函数 dU=Tds-pdv dH=Tds+vdp dF=-sdT-pdv dG=-sdT+vdp以上特征函数共有8个偏导数,即(),(),(),()v p s U U H H T s p T v s v s p∂∂∂∂==-==∂∂∂∂(),(),(),()v T p T F F G G s p s v TvTp∂∂∂∂=-=-=-=∂∂∂∂dG 、dF 、dv 、dH 为全微分,所以二阶偏导与求导顺序无关。