热力学微分关系式及实际气体的性质
- 格式:ppt
- 大小:1.96 MB
- 文档页数:102


第二部分工质的热力性质热力学函数的一般关系式由热力学基本定律引出的一些基本热力学状态函数(如能U、熵S)及其为某一研究方便而设的组合函数(如焓H、自由能F、自由焓G等)许多都是不可测量,必须将它们与可测量(如压力p、体积V、温度T等)联系起来,否则我们将得不到实际的结果,解决不了诸如上一章讲的最大功计算等一些具体的问题。
这就需要发展热力学的数学理论以将热力学基本定律应用到各种具体问题中去。
热力学函数一般关系式全微分性质+基本热力学关系式6.1状态函数的数学特性对于状态参数,当我们强调它们与独立变量的函数关系时,常称它们为状态函数。
从数学上说,状态函数必定具有全微分性质。
这一数学特性十分重要,利用它可导出一系列很有实用价值的热力学关系式。
下面我们扼要介绍全微分的一些基本定理设函数z f (x,y)具有全微分性质则必然有(1)互易关系令式(6-1 )中N(x,y)(6-2)互易关系与…dz 0等价。
它不仅是全微分的必要条件,而且是充分条件。
因此,可反过来检验某一物理量是否具有全微分。
(2)循环关系当保持z不变,即dz0时,由式(6-1),得zdx z zdy z 0dz dx dyx(6-1 ) M (x, y)故有 此式的功能是:若能直接求得两个偏导数,便可确定第三个 偏导数。
结果也很容易记忆,只需将三个变量依上、下、外 次序,即(zyx)(yxz)(xzy)循环就行了。
(3)变换关系两边同除以dx ,得立变量时,函数z(x,)对x 的偏导数。
上面的关系可用于它们 之间的变换。
这一关系式对于热力学公式的推导十分重要。
(4)链式关系按照函数求导法则,可有下述关系:式中: x y 是函数z (x,y)对x 的偏导数;:是以O')为独xxyy x x(6-3 ) 将式(6-1 )用于某第四个变量 不变的情况,可有dzz —dx z —dyz_z z y(6-4)(6-5 )(6-5a )这是在同一参数(如y)保持不变时,一些参数(z,x,,)循环求导所得偏导数间的关系。


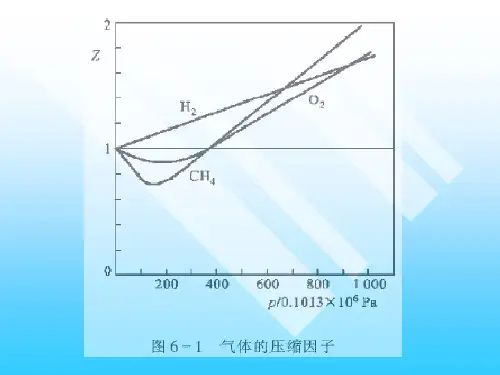




第六章实际气体的性质及热力学一般关系一、目的及要求:了解实际气体与理想气体之间差异产生的原因,掌握利用范德瓦尔方程表征实际气体的状态方程;掌握利用通用压缩因子图求解实际气体的状态参数,了解实际气体的热力学能、焓、熵等参数的表达式。
二、内容:6.1理想气体与实际气体的区别6.2范德瓦尔议程及R-K方程6.3对应态原理与通用压缩因子图6.4维里方程、麦克斯韦关系和热系数6.5热力学能、焓、熵及比热容的一般关系三、重点及难点:6.1了解热力学一般关系式及如何由可测量参数求不可测量参数;由易测量参数求不易测量参数。
6.2了解如何根据热力学理论来指导实验和整理实验数据,以减少实验次数,节省人力和物力。
6.3了解常用的实际气体状态方程,掌握范德瓦尔方程及R-K方程(包括其各项的物理意义)。
6.4掌握对比态原理,会计算对比参数并能利用通用压缩因子图进行实际气体的计算。
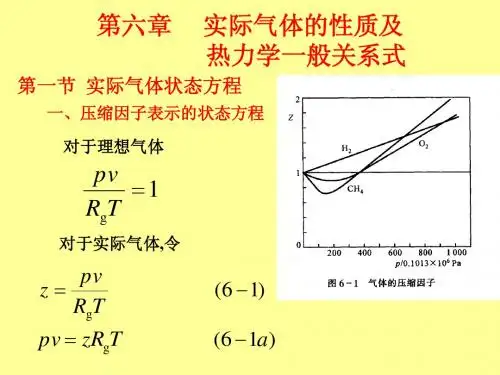
四、主要外语词汇:real gas五、本章节采用多媒体课件六、复习思考题及作业:思考题:1、实际气体性质与理想气体差异产生的原因是什么?在什么条件下才可以把实际气体作为理想气体处理?2、压缩因子Z的物理意义怎么理解?能否将Z当作常数处理?3、范德瓦尔方程的精度不高,但在实际气体状态方程的研究中范德瓦尔方程的地位却很高,为什么?4、什么叫做对应态原理?为什么引入对应态原理?什么是比参数?作业:6-2,6-4,6-5第六章实际气体的性质及热力学一般关系式分析工质的热力过程和热力循环时,需要确定工质的各种热力参数的数值,常用的热力参数中,只有p、v、T和c p等少数几种状态参数可由实验测定,而u、h、s等值是无法测量的,它们的值必须根据可测参数的值,按照一定的热力学关系加以确定。
在本章中,主要讨论了依据热力学第一和第二定律,运用数学工具导出的这些参数间的适用于任何工质的热力学一般关系式。
由于这些关系式常以微分或微商的形式表示,故又称之为微分关系式。
在此基础上还讨论了实际气体的性质及其参数计算。