第06章 热力学微分关系式

第二部分工质的热力性质六热力学函数的一般关系式由热力学基本定律引出的一些基本热力学状态函数（如内能U、熵S）及其为某一研究方便而设的组合函数（如焓H、自由能F、自由焓G等）许多都是不可测量，必须将它们与可测量（如压力p、体积V、温度T等）联系起来，否则我们将得不到实际的结果，解决不了诸如上一章讲的最大功计算等一些具体的问题。

这就需要发展热力学的数学理论以将热力学基本定律应用到各种具体问题中去。

热力学函数一般关系式 全微分性质+基本热力学关系式6.1 状态函数的数学特性对于状态参数，当我们强调它们与独立变量的函数关系时，常称它们为状态函数。

从数学上说，状态函数必定具有全微分性质。

这一数学特性十分重要，利用它可导出一系列很有实用价值的热力学关系式。

下面我们扼要介绍全微分的一些基本定理。

设函数),(y x f z =具有全微分性质dy y z dx x z dz xy ⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂= （6-1） 则必然有（1） 互易关系令式（6-1）中),(y x M x z y=⎪⎪⎭⎫ ⎝⎛∂∂， ),(y x N y z x =⎪⎪⎭⎫ ⎝⎛∂∂ 则 y x x N y M ⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂ （6-2）互易关系与⎰=0dz 等价。

它不仅是全微分的必要条件，而且是充分条件。

因此，可反过来检验某一物理量是否具有全微分。

（2） 循环关系当保持z 不变，即0=dz 时，由式（6-1），得0=⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂z xz y dy y z dx x z则 xy z y z x z x y ⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂ 故有 1-=⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂y z x z x x y y z （6-3）此式的功能是：若能直接求得两个偏导数，便可确定第三个偏导数。

结果也很容易记忆，只需将三个变量依上、下、外次序，即))()((xzy yxz zyx 循环就行了。

【最新整理，下载后即可编辑】第二部分 工质的热力性质六 热力学函数的一般关系式由热力学基本定律引出的一些基本热力学状态函数（如内能U 、熵S ）及其为某一研究方便而设的组合函数（如焓H 、自由能F 、自由焓G 等）许多都是不可测量，必须将它们与可测量（如压力p 、体积V 、温度T 等）联系起来，否则我们将得不到实际的结果，解决不了诸如上一章讲的最大功计算等一些具体的问题。

这就需要发展热力学的数学理论以将热力学基本定律应用到各种具体问题中去。

热力学函数一般关系式←全微分性质+基本热力学关系式6.1 状态函数的数学特性对于状态参数，当我们强调它们与独立变量的函数关系时，常称它们为状态函数。

从数学上说，状态函数必定具有全微分性质。

这一数学特性十分重要，利用它可导出一系列很有实用价值的热力学关系式。

下面我们扼要介绍全微分的一些基本定理。

设函数),(y x f z =具有全微分性质dy y z dx x z dz xy ⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂= （6-1）则必然有（1） 互易关系令式（6-1）中),(y x M x z y=⎪⎪⎭⎫ ⎝⎛∂∂， ),(y x N y z x =⎪⎪⎭⎫ ⎝⎛∂∂ 则 y x x N y M ⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂ （6-2）互易关系与⎰=0dz 等价。

它不仅是全微分的必要条件，而且是充分条件。

因此，可反过来检验某一物理量是否具有全微分。

（2） 循环关系当保持z 不变，即0=dz 时，由式（6-1），得0=⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂z xz y dy y z dx x z 则 xy z y z x z x y ⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂ 故有 1-=⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂y z xz x x y y z （6-3） 此式的功能是：若能直接求得两个偏导数，便可确定第三个偏导数。

第二部分工质的热力性质六热力学函数的一般关系式由热力学基本定律引出的一些基本热力学状态函数（如内能 U 、熵S）及其为某一研究方便而设的组合函数（如焓H 、自由能F、自由焓G等）许多都是不可测量，必须将它们与可测量（如压力 p 、体积V、温度T等）联系起来，否则我们将得不到实际的结果，解决不了诸如上一章讲的最大功计算等一些具体的问题。

这就需要发展热力学的数学理论以将热力学基本定律应用到各种具体问题中去。

热力学函数一般关系式全微分性质 +基本热力学关系式6.1状态函数的数学特性对于状态参数，当我们强调它们与独立变量的函数关系时，常称它们为状态函数。

从数学上说，状态函数必定具有全微分性质。

这一数学特性十分重要，利用它可导出一系列很有实用价值的热力学关系式。

下面我们扼要介绍全微分的一些基本定理。

设函数 z f ( x, y) 具有全微分性质z zdy （ 6-1）dz dxx y y x则必然有（1）互易关系令式（ 6-1）中z zM ( x, y) ，N (x, y)x y y xM N（ 6-2）则xy x y互易关系与 dz 0 等价。

它不仅是全微分的必要条件，而且是充分条件。

因此，可反过来检验某一物理量是否具有全微分。

（2）循环关系当保持 z 不变，即dz 0 时，由式（6-1），得zdx z zdy z 0x yy xzy x 则x z zy y xz y x1 （ 6-3）故有x zy x z y此式的功能是：若能直接求得两个偏导数，便可确定第三个偏导数。

结果也很容易记忆，只需将三个变量依上、下、外次序，即循环就行了。

（ 3）变换关系将式（ 6-1）用于某第四个变量不变的情况，可有z zdz dx dyxy yx两边同除以 dx ，得z z z y（ 6-4）x x y y x xz 是函数 z( x, y) 对x的偏导数；z 是以(x, ) 为式中：xx y独立变量时，函数z(x,) 对x的偏导数。

第五章热力学微分关系式研究热力学微分关系式的目的√ 易测量状态参数 √无法测量状态参数揭露各热力参数间的内在联系√ √ 理论研究 实验测试适用范围√简单可压缩纯物质系统纯物质具有固定的化学成分的物质空气 油和水 冰和液态水的混合物 液态空气和气态空气研究热力学微分关系式的目的√ 确定 ∆u, ∆h, ∆s 与可测参数（p,v,T,cp )之 间的关系，便于编制工质热力性质表。

√ 确定 cp , cv 与 p,v,T 的关系，用以建立 实际气体状态方程。

√ 确定 cp 与 cv 的关系，由易测的 cp 求得cv 。

√ 热力学微分关系式适用于任何工质，可用 其检验已有图表、状态方程的准确性。

§5-1 特征函数1、自由能和自由焓亥姆霍兹（Holmhotz）函数du = Tds − pdv = d (Ts ) − sdT − pdvd ( u − Ts ) = − sdT − pdv令 f = u − Ts 亥姆霍兹函数 F = U − TS df = − sdT − pdv f的物理意义: f的减少＝可逆等温过程的 膨胀功，或者说，f是可逆等温条件下 内能中能转变为功的那部分，也称亥姆 霍兹自由能亥姆霍兹（Holmhotz）函数令 f = u − Ts 亥姆霍兹函数 F = U − TS df = − sdT − pdvTs 是可逆等温条件下内能无法转变为功 的那部分，故称为束缚能亥姆霍兹，H. von Hermann von Helmholtz（1821-1894） 德国 物理学家 生理学家 化学热力学吉布斯（Gibbs）函数dh = Tds + vdp = d (Ts ) − sdT + vdpd ( h − Ts ) = − sdT + vdp令 g = h − Ts 吉布斯函数 G = H − TS dg = − sdT + vdp g = g (T , p ) 是特征函数 g的物理意义: g的减少＝可逆等温过程 对外的技术功，或者说，g是可逆等温 条件下焓中能转变为功的那部分，也称 吉布斯自由焓吉布斯，J. W Josiah Willard Gibbs（1839-1903） 美国 物理学家吉布斯函数 吉布斯相律 吉布斯佯谬§5-1特征函数简单可压缩系统，两个独立变量。

至今讨论中常应用的八个热力学函数--p、V、T、U、H、S、A、G。

其中 U 和 S 分别由热力学第一定律和第二定律导出；H、A、G 则由定义得来。

而 U、H、A、G 为具有能量量纲的函数。

这些热力学函数间通过一定关系式相互联系着。

基本热力学关系式共有十一个（以下分别用公式左边括弧中的数字标明）。

从这十一个基本关系式出发，可以导出许多其它衍生关系式，它们表示出各不同物理量间的相互关系，利用它们可以帮助我们由易于直接测量的物理量出发以计算难于直接测量的物理量的数值。

由定义可得如下三个关系式：(1) (3-136)(2) (3-137)(3) (3-138)又由热力学第一定律、第二定律联合公式，在无非膨胀功条件下：将它和式(3-136)、(3-137)、(3-138)联系起来：即可得以下四个一组被称为恒组成均相封闭系统的热力学基本方程。

又称 Gibbs 方程。

(4) (3-139)(5) (3-140)(6) (3-141)(7) (3-142)这四个基本方程均不受可逆过程的限制，因为 U、H、A、G 等随着相应两个独立的状态函数变化而变化，因而与变化的具体途径（可逆或不可逆）无关，自然亦可用于不可逆过程。

公式虽然是四个，但式(5)、(6)、(7)实际上是基本公式(4)在不同条件下的表示形式。

根据全微分定义可有如下关系：(3-143)(3-144)(3-145)(3-146)式(3-139)与式(3-143)对比、式(3-140)与式(3-144)对比、式(3-141)与式(3-145)对比、式(3-142)与式(3-146)对比，可得如下关系(或称"对应系数式")：(3-147)(3-148)(3-149)和 (3-150)如分别将尤拉(Euler)定则：应用于热力学基本方程(4)、(5)、(6)、(7)可得如下四式：(8) (3-151)(9) (3-152)(10) (3-153)(11) (3-154)这四式常称为"麦克斯威关系式"。

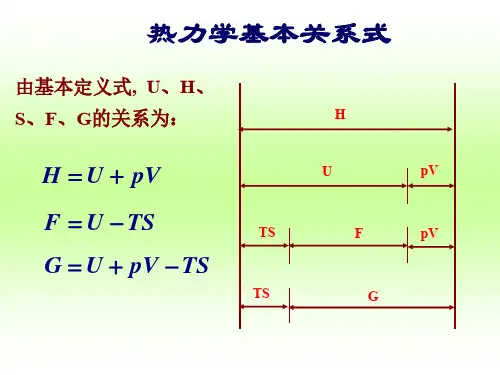
第六章 热力学微分关系式1．基本概念自由能：F =U －TS ，F 称为自由能，或称亥姆霍兹（Helmholtz ）函数。

自由焓：令G = H －TS ，G 称为自由焓，或称吉布斯（Gibbs ）函数。

2．重要公式热力学能的基本关系式：V p U W U Q d d d +=+=δδV p S T U d d d -=焓的基本关系式：p V V p U H d d d d ++= p V S T H d d d +=自由能基本关系式：V p T S F d d d --=自由焓的基本关系式：P V T S G d d d +-=麦克斯韦关系式：v s )()(S p V T ∂∂-=∂∂ p s )()(S V p T ∂∂=∂∂ v T )()(T pV S ∂∂=∂∂ p T )()(TV p S ∂∂=∂∂-热系数：⎪⎪⎪⎭⎪⎪⎪⎬⎫∂∂-=∂∂=∂∂=T p v )(1)(1)(1p v v T v v Tp p μβα式中α——压力温度系数；v )(Tp∂∂——物质在定容下压力随温度的变化率； β——容积膨胀系数，或称热膨胀系数；p )(Tv∂∂——物质在定压下比体积随温度的变化率；μ——定温压缩系数，或简称压缩系数；T )(pv∂∂——物质在定温下比体积随压力的变化率，表示物质在定温条件下受压后的压缩性。

这个偏导数为负值，加负号后，μ仍为正值。

熵方程：v TpT T c s d )(d d v v ∂∂+=p TvT Tc sd )(d d p p ∂∂-=v vT T c p p TT c s d )(d )(d p p v v ∂∂+∂∂=焓方程：p TvT v T c h d ])([d d p p ∂∂-+= 热力学能的微分方程式：⎰⎰-∂∂+=-2121d ])([d v v 12v v T T v p TpT T c u u 热量的微分方程式：v v p p d d ()d d d ()d p q T s c T T v Tvq T s c T T pTδδ∂==+∂∂==-∂上述两式适用于任意物质的任何可逆过程。

微分关系式微分关系式是微积分中的一个重要概念，用于描述函数之间的关系。

它通过求导数的方式，揭示了函数变化率之间的联系。

本文将介绍微分关系式的定义、性质和应用，以及它在实际问题中的应用。

一、微分关系式的定义微分关系式是指函数之间的导数关系。

设函数y=f(x)，若存在另一个函数y=g(x)，且f'(x)=g(x)，则称g(x)是f(x)的微分关系式。

微分关系式表示了函数f(x)在某一点处的瞬时变化率与函数g(x)之间的关系。

1. 反函数关系：若f(x)的微分关系式为g(x)，则g(x)的微分关系式为f(x)。

2. 线性性质：若f(x)的微分关系式为g(x)，h(x)的微分关系式为k(x)，则af(x)+bh(x)的微分关系式为ag(x)+bk(x)，其中a、b为常数。

3. 复合函数关系：若f(x)的微分关系式为g(x)，h(x)是由函数f(x)和g(x)复合而成的新函数，则h(x)的微分关系式为g(f(x))。

三、微分关系式的应用微分关系式在实际问题中有着广泛的应用，特别是在物理学、经济学、生物学等领域。

1. 物理学中的应用：微分关系式可以用来描述物体的运动状态。

例如，对于匀速直线运动，位移与时间的关系可以通过微分关系式来表示。

2. 经济学中的应用：微分关系式可以用来分析经济变量之间的关系，比如价格与需求之间的关系。

通过对价格的微分，可以得到需求的弹性与价格的变化率之间的关系。

3. 生物学中的应用：微分关系式可以用来描述生物体的生长和变化过程。

例如，通过对生物体质量的微分，可以得到生物体生长速率与时间的关系。

四、微分关系式的计算方法计算微分关系式可以使用导数的定义和性质，以及链式法则、乘积法则、商规则等微分运算法则。

这些法则可以简化复杂函数的微分计算，使得微分关系式的求解更加方便快捷。

五、总结微分关系式是微积分中的重要概念，用于描述函数之间的导数关系。

它具有反函数关系、线性性质和复合函数关系等性质。