5.4 梁的整体稳定1
- 格式:doc
- 大小:3.82 MB
- 文档页数:11

钢梁整体稳定性验算步骤1. 根据《钢结构设计规范》(GB 50017-2003)4.2.1条,判断是否可不计算梁的整体稳定性。
2. 如需要计算2.1 等截面焊接工字形和轧制H 型钢简支梁xyxy(a)双轴对称焊接工字形截面(b)加强受压翼缘的单轴对称焊接工字形截面y (c)加强受拉翼缘的单轴对称焊接工字形截面y (d)轧制H 型钢截面1)根据表B.1注1,求ξ。
ξl 1——H 型钢或等截面工字形简支梁受压翼缘的自由长度,对跨中无侧向支承点的梁,l 1为其跨度;对跨中有侧向支撑点的梁,l 1为受压翼缘侧向支承点间的距离(梁的支座处视为有侧身支承)。
b 1——截面宽度。
2)根据表B.1,求βb。
3)根据公式B.1-1注,求I1和I2,求αb。
如果αb>0.8,根据表B.1注6,调整βb。
4)根据公式B.1-1注,计算ηb。
5)根据公式B.1-1,计算φb。
6)如果φb>0.6,根据公式B.1-2,采用φ’b代替φb。
7)根据公式4.2.2,验算稳定性。
2.2 轧制普通工字钢简支梁1)根据表B.2选取φb。
2)如果φb>0.6,根据公式B.1-2,采用φ’b代替φb。
3)根据公式4.2.2,验算稳定性。
2.3 轧制槽钢简支梁1)根据公式B.3,计算φb。
2)如果φb>0.6,根据公式B.1-2,采用φ’b代替φb。
3)根据公式4.2.2,验算稳定性。
2.4 双轴对称工字形等截面(含H型钢)悬臂梁1)根据表B.1注1,求ξ。
ξl1——悬臂梁的悬伸长度。
b1——截面宽度。
2)根据表B.4,求βb。
3)根据公式B.1-1,计算φb。
4)如果φb>0.6,根据公式B.1-2,采用φ’b代替φb。
5)根据公式4.2.2,验算稳定性。
2.5 受弯构件整体稳定系数的近似计算(均匀弯曲,)2.5.1 工字形截面(含H型钢)双轴对称1)根据公式B.5-1,计算φb,当φb>0.6时,不必根据公式B.1-2,采用φ’b 代替φb,当φb>1.0,取φb=1.0。
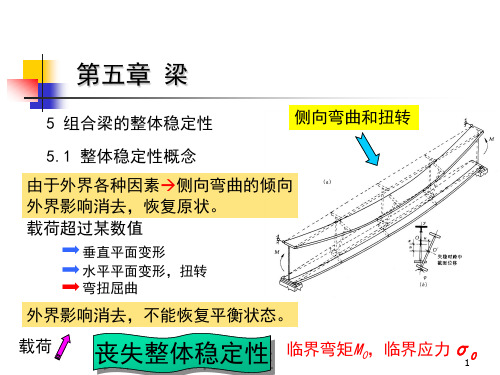

P1875.1解:1.计算截面特征值:A=2⨯300⨯16+1200⨯10=21600mm 2I x =(300⨯12323-290⨯12003)/12=4.989⨯109mm 4W x = I x /616=8.099⨯106 mm 3Iy=(1200⨯103+2⨯16⨯3003)/12=72.10⨯106 mm 4iy=( Iy/A)1/2=57.76mmλy=l 1/iy=7200/57.76=124.65梁自重q=A γ=21.6⨯10-6⨯77=1.663⨯10-3kN/m2.求梁最大弯矩M=P l /4=(设计值)650⨯7.2/4+1.2⨯1.663⨯10-3⨯7.22/8=1170+12.93=1182.93kN.m3.验算梁的整体稳定跨中无侧向支撑,荷载作用在梁上翼缘,钢材Q235l 1/b=24>13 不满足表5.9不需要验算的条件要求满足 σ=M/ϕb W ≤f焊接工字组合截面整体稳定系数βb 梁整体稳定的等效临界弯矩系数计算 ξ=l 1t 1/b 1h=7200⨯16/300⨯1232=0.312<2查P122表5.6 得 βb =0.73+0.18ξ=0.786,ηb ——截面不对称系数,ηb =0。
=0.765>0.6 (截面已进入塑性,修正ϕ'b )ϕ'b =1.07-0.282/ϕb =0.701σ=M/ϕ'b W=1182.93⨯106/0.701⨯8.099⨯106 =208.35 N/mm 2<215 N/mm 2满足要求 (结论要给)5.2解:y b 21y x 2yb b 235])4.4(1[4320f h t W Ah ⋅++⋅⋅=ηλλβφy b 21y x 2yb b 235])4.4(1[4320f h t W Ah ⋅++⋅⋅=ηλλβφ1.初选截面:标准值q d=3⨯3=9kN/m;q L=20⨯3=60KN/m设计值q d=1.2⨯3⨯3=10.8kN/m;q L=1.3⨯20⨯3=78KN/mM=(10.8+78)⨯62/8=399.6 kN.m钢材Q345-B,f =310N/ mm2W=M/f =399.6⨯106/310=1289⨯103/ mm3选择HM450⨯200(446⨯199) ,梁自重84.95kg/m2.验算构件:(1) 整体稳定钢筋混凝土板与次梁焊接,能保证整体稳定。



5.4.3 整体稳定性的验算方法1.计算公式由求得的临界弯矩可求得临界应力:(5.4.2)式中:为按受压纤维确定的梁毛截面抵抗矩。
保证梁整体稳定的条件是:(5.4.3)或:(5.4.4)式中:M x——绕强轴作用的最大弯矩;——梁的整体稳定系数。
双轴对称工字型截面简支梁受纯弯曲荷载作用时:(5.4.5)式中:——梁在侧向支承点间对截面弱轴(y轴)的长细比;——受压翼缘的自由长度;——梁的毛截面对y轴的截面回转半径;——梁的毛截面面积;——梁的截面高度和受压翼缘厚度(见图5-4-2)。
对于单轴对称工字型截面(图5-4-2b、c),应考虑截面不对称影响系数,对于其它种类的荷载和荷载的不同作用位置,还应乘以修正系数,从而可得通式为:(5.4.6)图5-4-2 焊接工字形截面式中:——等效弯矩系数,参见[表5-4-4];——截面不对称影响系数,双轴对称工字型截面,=0;加强受压翼缘的工字型截面,(图5-4-2b);加强受拉翼缘的工字型截面,(图5-4-2c);和分别为受压翼缘和受拉翼缘对y轴的惯性矩。
上述公式是按弹性工作阶段给出的,当时,已超出了弹性范围,应按下式修正或查[表5-4-1],用代替。
表(5-4-1)整体稳定系数值(5.4.7)对于轧制普通工字钢简支梁的整体稳定系数,同样应以代替。
在两个主平面内受弯曲作用的工字型截面构件,应按下式计算整体稳定性:(5.4.8) 2. 计算梁的整体稳定系数的简化方法Ⅰ热轧普通工字钢简支梁,可直接查[表5-4-2]。
Ⅱ轧制槽钢简支梁的整体稳定系数,均按下式计算:(5.4.9)式中:h﹑b﹑t——分别为槽钢截面的高度﹑翼缘宽度和平均厚度。
3. 不必计算整体稳定性的情况当梁的整体稳定性系数=1.0时,梁就不可能丧失整体稳定性,也不必计算梁的整体稳定性,具体条件如下:Ⅰ有铺板(各种钢筋混凝土板和钢板)密铺在梁的受压翼缘上并与其牢固相连接,能阻止梁受压翼缘的侧向位移时;Ⅱ工字型截面简支梁受压翼缘的自由长度与其宽度b1之比不超过[表5-4-3]所规定的数值时。
3.梁的整体稳定系数b ϕ计算(1) 等截面焊接工字形和轧制H 型钢简支梁等截面焊接工字形和轧制H 型钢简支梁(图3-3-6)的整体稳定系数b ϕ,应按下式计算:(a)双轴对称焊接工字形截面 (b)加强受压翼缘的单轴对称焊接工字形截面 (c)加强受拉翼缘的单轴对称焊接工字形截面 (d)轧制H 型钢截面图3-3-6 焊接工字形截面和轧制H 型钢截面y b y x y b b f h t W Ah 2354.414320212⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛+⋅=ηλλβϕ (3-3-11) 式中b β——梁整体稳定的等效临界弯矩系数,按表3-3-3采用;y λ——梁在侧向支承点间对截面弱轴y-y 轴的长细比,y y i l /1=λ,y i 为梁毛截面对y 轴的截面回转半径,1l 为梁受压翼缘的自由长度;A ——梁的毛截面面积;h 、1t ——梁截面的全高和受压翼缘厚度; b η——截面不对称影响系数:对双轴对称工字形截面(见图3-3-6a 、d ):0=b η 对单轴对称工字形截面(见图3-3-6b 、c ) 加强受压翼缘时:()128.0-=b b αη 加强受拉翼缘时:12-=b b αη211I I I b +=α,1I 和2I 分别为受压翼缘和受拉翼缘对y 轴的惯性矩。
公式(3-3-11)也适用于等截面铆接(或高强度螺栓连接)简支梁,其受压翼缘厚度1t包括翼缘角钢厚度在内。
当按公式(3-3-11)算得的b ϕ值大于0.6时,应采用下式计算的'b ϕ替代b ϕ值:0.1282.007.1'≤-=b b ϕϕ (3-3-12)表3-3-3 H 型钢和等截面工字形简支梁的系数b β 项次 侧向支承荷 载0.2≤ξ 0.2>ξ适用范围1 跨中无侧向支承 均布荷载作用在上翼缘 ξ13.069.0+ 0.95 图3-3-6a ,b 和d 截面2 下翼缘ξ20.073.1- 1.33 3 集中荷载作用在 上翼缘 ξ18.073.0+ 1.09 4 下翼缘 ξ28.023.2-1.675 跨度中点有一个侧向支承点均布荷载作用在 上翼缘 1.15图3-3-6中所有截面6 下翼缘 1.407 集中荷载作用在截面高度上任意位置1.75 8 跨中有不少于两个等距离侧向支承点任意荷载作用在 上翼缘1.20 9下翼缘 1.4010 梁端有弯矩,但跨中无荷载作用212123.005.175.1⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛-M M M M 但3.2≤注:①hb t l 111=ξ。
5.4 梁的整体稳定5.4.1 梁的整体失稳现象梁主要是用于承受弯距,为了提高梁的抗弯强度,节省钢材,梁的截面一般做成高而窄的形式。
如图5.18所示的工字形截面梁,荷载作用在其最大刚度平面内,当荷载较小时,梁的弯曲平衡状态是稳定的。
虽然外界各种因素会使梁产生微小的侧向弯曲和扭转变形,但外界影响消失后,梁仍能恢复原来的弯曲平衡状态。
然而,当荷载增大到某一数值后,梁在弯矩作用平面内弯曲的同时,将突然发生侧向的弯曲和扭转变形,并丧失继续承载的能力,这种现象称为梁的整体失稳或弯扭屈曲。
梁维持其稳定平衡状态所承担的最大荷载或最大弯矩,称为临界荷载或临界弯矩。
图5.18 梁的整体失稳横向荷载的临界值和它沿梁高的作用位置有关。
当荷载作用在上翼缘时,如图5-19(a)所示,在梁产生微小侧向位移和扭转的情况下,荷载F将产生绕剪力中心的附加扭矩Fe,它将对梁侧向弯曲和扭转起促进作用,会加速梁丧失整体稳定。
但当荷载F作用在梁的下翼缘时,如图5-19(b)所示,它将产生反方向的附加扭矩Fe,有利于阻止梁的侧向弯曲扭转,延缓梁丧失整体稳定。
因此,后者的临界荷载(或临界弯矩)将高于前者。
图5.19 荷载位置对整体失稳的影响5.4.2 梁的临界荷载图5-12(a)所示为一两端简支双轴对称工字形截面纯弯曲梁,梁两端均受弯矩M作用,弯矩沿梁长均分布。
这里所指的“简支”符合夹支条件,即支座处截面可自由翘曲,能绕x轴和y轴转动,但不能绕z轴转动,也不能侧向移第动。
图5-12 梁的侧向弯扭屈曲设固定坐标为x、y、z,弯矩M达到一定数值屈曲变形后,相应的移动坐标为'x、'y、'z,截面形心在x、y轴方向的位移u、v,截面扭转角为 。
在图5-12(b)和图5-12(d)中,弯矩用双箭头向量表示,其方向按向量的右手规则确定。
梁在最大刚度平面内(z y ''平面)发生弯曲(图5-12(c )),平衡方程M dzvd EI =-22x (5-20)梁在z x ''平面内发生侧向弯曲(图5-12(d )),平衡方程ϕM dzud EI =-22y (5-21)式中:y x I I ,——梁对x 轴和y 轴的毛截面惯性矩。
由于梁端部夹支,中部任意截面扭转时,纵向纤维发生了弯曲,属于约束扭转。
根据式(5-19),得扭转的微分方程z u M z GI zEI d d d d d d t 33ω=+-ϕϕ (5-22) 可得到ϕ的弯扭屈曲微分方程0y 22t 44ω=--ϕϕϕEI M dzd GI dz d EI (5-23)假设两端简支梁的扭转角为正弦曲线分布,即lzC πϕsin=将ϕ、ϕ的二阶导数和四阶导数代入式(5-23)中,得0siny 22t 4ω=⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛l z C EI M l GI l EI πππ 使上式在任何z 值都成立的条件是方括号中数值为零,即0y22t 4ω=-⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛EI M l GI l EI ππ上式中的M 就是双轴对称工字形截面简支梁纯弯曲时的临界弯矩t2ω2t y cr 1GI l EI GI EI lM ππ+=(5-24)式中:y EI ——侧向抗弯刚度;t GI ——自由扭转刚度; ωEI ——翘曲刚度。
式(5-24)是根据双轴对称工字形截面简支梁纯弯曲时,根据弹性稳定理论推导的临界弯矩。
对于加强梁的受压上翼缘,有利于提高梁的整体稳定。
单轴对称截面简支梁(图5-13)在不同荷载类型作用下,根据弹性稳定理论可推导出其临界弯矩的通用计算公式()⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+++++=ω2t 2yω2y32y 322y 21cr 1EIGI l I I C a C C a C lEI C M πββπ (5-25) ()022Axy d 21y A y x y I -+=⎰β式中:y β——单轴对称截面的一种几何特性,当为双轴对称时,0y =β;0y ——剪切中心的纵坐标,y22110I h I h I y --=;正值时,剪切中心在形心之下,负值时,在形心之上;a ——荷载作用点与剪切中心之间的距离,当荷载作用点在剪切中心以下时,取正值,反之取负值;21I I ,——分别为受压翼缘和受拉翼缘对y 轴的惯性矩,12/12/32223111b t I b t I ==,;21h h ,——分别为受压翼缘和受拉翼缘形心至整个截面形心的距离;321C C C ,,——根据荷载类型而定的系数,其值如表5-2所示。
图5-13 单轴对称截面上述的所有纵坐标均以截面的形心为原点,y 轴指向下方时为正向。
式(5-25)已为国外许多试验研究所证实,并为许多国家制订设计规范时所参考采用。
表5-2系数和,321C C C由临界弯矩M cr 的计算公式(5-25)可见,梁整体稳定的临界荷载与梁的侧向抗弯刚度、抗扭刚度、翘曲刚度、梁截面形状、荷载类型、荷载作用位置以及梁的跨度有关。
5.4.3 梁的整体稳定系数由式(5-24)可得双轴对称工字形截面简支梁的临界应力xcrcr W M =σ (5-26) 式中:x W ——梁对x 轴的毛截面模量。
梁的整体稳定应满足下式f f f W M b Ry ycr R cr x x ϕγσγσσ==≤=式中:b ϕ——梁的整体稳定系数,y cr b /f σϕ=。
为了简化计算,《规范》取213i i t 31325.1At t b I ≈=∑ 42y ωh I I =式中:A ——梁的毛截面面积。
代入数值23mm N/10206⨯=E ,E /G =2.6,令2y y Ai I =,y y 1/λ=i l ,并取Q235钢的2y mm N/235=f ,得到稳定系数的近似值2b 4320y λϕ=y21y x 2354.41f h t W Ah⎪⎪⎭⎫ ⎝⎛+λ (5-27) 式中:1t ——受压翼缘厚度。
实际工程中梁受纯弯曲的情况很少,当梁受任意横向荷载作用时,梁的临界弯矩理论值应按式(5.25)计算,并可以求得相应的稳定系数φb 。
但这样计算很繁,通常选取一些常用的截面尺寸,应用计算机进行计算和数值统计分析,得出了不同荷载作用下的稳定系数和纯弯曲作用下稳定系数的比值βb 。
同时为了能够应用于单轴对称焊接工字形截面简支梁的一般情况,梁的整体稳定系数φb 按下式计算y212y b 235)4.4(14320f h t W Ah b y x b ⎥⎥⎦⎤⎢⎢⎣⎡++=ηλλβϕ (5.27) 式中 βb ——梁整体稳定的等效临界弯矩系数,按表5.4采用;λy ——梁在侧向支承点间对截面弱轴y —y 的长细比; A ——梁的毛截面面积;h 、t 1——梁截面的全高和受压翼缘厚度;ηb ——截面不对称影响系数;对双轴对称截面,如图5.21(a)、(d),ηb 为0;对单轴对称工字形截面,如图5.21(b)、(c):加强受压翼缘,ηb =0.8(2αb -1),加强受拉翼缘,ηb =2αb -1,211I I I b +=α,I 1、I 2分别为受压翼缘和受拉翼缘对y 轴的惯性矩。
图5.21 焊接工字形和轧制H 型钢截面(a)双轴对称焊接工字形截面;(b)加强受压翼缘的单轴对称焊接工字形截面;(c)加强受拉翼缘的单轴对称焊接工字形截面;(d)轧制H 型钢截面上述整体稳定系数是按弹性稳定理论求得的。
研究证明,当计算求得的φb 值大于0.6时,梁已进入非弹性工作阶段,其临界应力有明显的降低,必须对b ϕ进行修正。
当按公式5.27算得的φb 值大于0.6时,应用'b ϕ代替φb 值进行梁的整体稳定计算0.1282.007.1'≤-=bb ϕϕ (5.28)轧制普通工字钢简支梁的整体稳定系数b ϕ应按表5.5采用,当所得的b ϕ值大于0.6时,应按式(5.28)计算的'b ϕ代替b ϕ值。
轧制槽钢简支梁的整体稳定系数,不论荷载的形式和荷载作用点在截面高度上的位置,均可按式(5.29)计算yb f h l bt 2355701⋅=ϕ (5.29) 式中 h 、b 、t ——分别为槽钢截面的高度、翼缘宽度和平均厚度。
按式(5.29)算得的b ϕ大于0.6时,应按式(5.28)算得相应的'b ϕ代替b ϕ值。
双轴对称工字形等截面(含H 型钢)悬臂梁的整体稳定系数,可按公式(5.27)计算,但式中系数b β按表5.6查得;1/y y l i λ=,(l 1为悬臂梁的悬伸长度)。
当求得的b ϕ大于0.6时,应按公式(5.28)算得相应的'b ϕ代替b ϕ值。
5.4.4 梁的整体稳定系数的近似计算承受均布弯矩的梁,当y λ≤b ϕ可按下列近似公式计算: ①.工字形截面(含H 型钢) 双轴对称时:21.0744000235y yb f λϕ=-⋅(5.30)单轴对称时:()21.0720.144000235y y xb b f W Ah λϕα=-⋅⋅+ (5.31)②.T 形截面(弯矩作用在对称轴平面,绕x 轴) 弯矩使翼缘受压时,双角钢T 形截面:10.0017b ϕλ=- (5.32)弯矩使翼缘受压时,剖分T 型钢和两板组合T 形截面:10.0022b ϕλ=- (5.33)弯矩使翼缘受拉且腹板宽厚比不大于10.0005b ϕλ=- (5.34)按公式(5.30)至公式(5.34)算得的b ϕ值大于0.6时,不需按式(5.28)换算成'b ϕ值;当按公式(5.30)和公式(5.31)算得的b ϕ值大于1.0时,取b ϕ=1.0。
5.4.5 梁整体稳定的保证如果能阻止梁的受压翼缘的侧向位移时,梁就不会丧失整体稳定,因此可不必计算梁的整体稳定性。
当梁上有密铺的刚性铺板(楼盖梁的楼面板或公路桥、人行天桥的面板等)时,应使之与梁的受压翼缘连牢[图5.19(a )];若无刚性铺板或铺板与梁受压翼缘连接不可靠,则应设置平面支撑[图5.19(b )]。
楼盖或工作平台梁格的平面支撑有横向平面支撑和纵向平面支撑两种,横向支撑使主梁受压翼缘的自由长度由其跨长减小为l 1(次梁间距);纵向支撑是为了保证整个楼面的横向刚度。
当符合下列情况之一时,可不计算梁的整体稳定性:(1)有刚性铺板(各种钢筋混凝土板或钢板)密铺在梁的受压翼缘上并与其牢固相连,能阻止梁受压翼缘的侧向位移。
(2)H 型钢或等截面工字形截面简支梁受压翼缘的自由长度l 1与其宽度b 1之比不超过表5.3所规定的数值时。
(3)两端简支的箱形截面受弯构件,当截面高度h 与两腹板的间距b 0(图5.20),满足h/b 0≤6,l 1/b 0≤95(235/f y )时,梁的整体稳定性能够得到保证,不必进行计算。