电磁波动方程和平面电磁波
- 格式:pdf
- 大小:325.21 KB
- 文档页数:11


§16-5 电磁波1. 平面电磁波的波动方程变化的电场和变化的磁场不断地交替产生,由近及远以有限的速度在空间传播,形成电磁波。
最初由麦克斯韦在理论上预言,1888年赫兹进行了实验证实。
在无限大均匀绝缘介质(或真空)中,ρ=0,δ=0,且介电常量ε和磁导率μ是常量。
麦克斯韦方程简化为:00S d E S d D =∂∂+∂∂+∂∂→=⋅=⋅∫∫z E y E x E z y x G G G G ε00S d H S d B =∂∂+∂∂+∂∂→=⋅=⋅∫∫zH y H x H zy x G G G G μD ρ∇•=JG 0B ∇•=J G平面电磁波的波动方程S d B d E G G G G ⋅∂∂−=⋅∫∫t l ⎪⎪⎪⎩⎪⎪⎪⎨⎧∂∂−=∂∂−∂∂∂∂−=∂∂−∂∂∂∂−=∂∂−∂∂→t H y E x E t H x E z E t H z E y E z x y y zx x yz μμμDH d dS l t ∂⋅=⋅∂∫∫G G G G v ⎪⎪⎪⎩⎪⎪⎪⎨⎧∂∂=∂∂−∂∂∂∂=∂∂−∂∂∂∂=∂∂−∂∂→t E y H x H tE x H z H t E z H y H zx y y z x x yz εεεt B E ∂∂−=×∇c D H j t ∂∇×=+∂JG JJ G J J G讨论一维问题,场量E 和H 是坐标x 和时间t 的函数。
前述方程组可简化为:⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫∂∂=∂∂∂∂=∂∂∂∂=∂∂−∂∂−=∂∂=∂∂=∂∂=∂∂=∂∂t E x H t H x E t E x H t H x E tH x H tE x E z y y z y zz y xx x x εμεμ,(IV),(III)0,0(II)0,0(I)经过一系列变换,得到22221xE tE y y ∂∂=∂∂εμ222221x H tH z z∂∂=∂∂εμ表明变化电磁场E y 和H z 是按波动形式传播。








第六章主平面电磁波要 内 容 9学时平面电磁波电磁波:变化的电磁场脱离场源后在空间的传播 平面电磁波:等相位面为平面构成的电磁波 均匀平面电磁波:等相位面上E、H 处处相等的 电磁波 若电磁波沿 x 轴方向传播,则H=H(x,t),E=E(x,t) 平面电磁波知识结构框图电磁场基本方程组 电磁波动方程 均匀平面电磁波的传播特性平面电磁波的基本特性1. 理想介质中的均匀平面波 2. 损耗媒质中的均匀平面波 3. 均匀平面波的极化 4. 均匀平面波对平面边界的垂直入射 5. 均匀平面波对平面边界的斜入射 6. 各向异性媒质中的均匀平面波1-120 2-120理想介质中均匀平面波 平面电磁波的极化导电媒质中均匀平面波平面电磁波的垂直入射平面电磁波的斜入射各向异性媒质中的均匀平面波x方向传播的一组均匀平面波3-120平面电磁波知识结构框图数的媒质, σ → ∞ 的媒质称为理想导体。
σ 介 于两者之间的媒质称为有损耗媒质或导电媒质。
6.1 理想介质中的均匀平面波 理想介质是指电导率 σ = 0 ,ε 、 μ 为实常6.1.1波动方程的解其通解为假设电磁场沿着 Z 轴方向传播,且电场仅有指向 X 轴 的方向分量,则磁场必只有 Y 方向的分量,即:z z E x = f1 (t − ) + f 2 (t + ) v v ∂ 2 Ex + β 2 Ex = 0 ∂z 2对于时谐变电磁场:E = ex E x ( z, t )波动方程H = ey H y (z,t)其通解为 则平面波是指波前面,即等相位面或者波前 阵是平面的波。
均匀平面波是指波前面上场量振 幅处处相等的波。
本节介绍最简单的情况,即介绍无源、均 匀(homogeneous)(媒质参数与位置无关)、 线性(linear)(媒质参数与场强大小无关)、 各向同性(isotropic)(媒质参数与场强方向无 关)的无限大理想介质中的时谐平面波。
4-120 5-120则∂E 2 =0 ∂t 2 ∂E 2 ∇ 2 E x − με 2x = 0 ∂t 2 ∂ E x 1 ∂E x2 − =0 ∂z 2 v 2 ∂t 2 ∇ 2 E − με其中: v =其中: β = ω μ εEx = Ex + e− jβ z + Ex − e+ jβ zE x = E x+ cos(ω t − β z ) + E x− cos(ω t + β z )对应的磁场为1∇ × E = −μ6-120με∂H ∂t∂H y ∂E x = −μ ∂z ∂t对应的磁场为∇ × E = −μ其通解为∂H ∂t∂H y ∂E x = −μ ∂z ∂t考察电场的一个分量 ,瞬时值表达式为:Ex ( z, t ) = Ex+ cos(ωt − β z + ϕx )其中Hy =β ⎡ E + cos(ω t − β z ) − E x− cos(ω t + β z ) ⎤ ⎦ ωμ ⎣ xωt 为时间相位 , β z 为空间相位 , ϕ x 是初始相位。
电磁波动方程和平面电磁波
电工基础教研室周学
本节的研究目的
掌握无源空间线性各向同性均匀介质中波动方程的推导;
掌握等相面,平面波,均匀平面波概念;掌握均匀平面电磁波的基本特征。
本节的研究内容
一、电磁波动方程
二、均匀平面电磁波
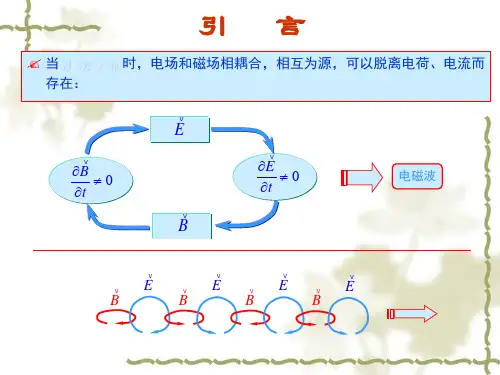
波动是电磁场的基本属性当时,电场和磁场相耦合,相互为源,可以脱离电荷、电流,以波的形式存在于空间中。
0/≠∂∂t 0≠∂∂t B 0≠∂∂t
E E
B 电磁波
⎪⎪⎩⎪⎪⎨⎧=∂∂-∇=∂∂-∇010*******
22t E c E t H c H
电磁波的波段划分及其应用名称频率范围波长范围典型业务
甚低频VLF[超长波] 3~30KHz100~10km导航,声纳低频LF[长波,LW] 30~300KHz10~1km导航,频标中频MF[中波, MW] 300~3000KHz1km~100m AM, 海上通信高频HF[短波, SW] 3~30MHz100m~10m AM, 通信
甚高频VHF[超短波] 30~300MHz10~1m TV, FM, MC 特高频UHF[微波] 300~3000MHz100~10cm TV, MC, GPS 超高频SHF[微波] 3~30GHz10~1cm通信,雷达
极高频EHF[微波] 30~300GHz10~1mm通信, 雷达
光频[光波] 1~50THz300~0.006 m光纤通信
研究电磁波在空间的传播规律和特性,就是讨论由电磁场基本方程组导出的电磁波动方程在给定条件下的解。
00E H E t H E t H E γεμ⎧∂∇⨯=+⎪∂⎪∂⎪∇⨯=-⎨∂⎪∇⋅=⎪⎪∇⋅=⎩D E B H
J E εμγ⎧=⎪=⎨⎪=⎩在无源空间中,假设媒质是各向同性、线性、均匀的,则
2
2222200H H H t t E E E t t μγμεμγμε⎧∂∂∇--=⎪⎪∂∂⎨∂∂⎪∇--=⎪∂∂⎩无源空间的电磁波动方程,研究电磁波问题的基础
t 等相位面:在电磁波传播过程中,对应于每一时刻,空间电磁场中电场或磁场具有相同相位的点构成等相位面,或波阵面。
E H 平面电磁波:等相位面为平面的电磁波称为平面电磁波。
均匀平面电磁波:在平面波的等相位面的每一点上,电场均相同,磁场也均相同,则这样的电磁波称为均匀平面电磁波。
E H 几个重要概念:
远离单元偶极子处的电磁波在小范围内可近似地看成均匀平面电磁波。
各种复杂的电磁波可看成由许多均匀平面电磁波迭加而成。
假设均匀平面电磁波的等相位面与yOz 平面平行
则,满足的一维波动方程为:沿x 方向传播的一组均匀平面波
(,)E x t (,)H x t 22
22222200H H H x t t E E E x t t μγμεμγμε⎧∂∂∂--=⎪⎪∂∂∂⎨∂∂∂⎪--=⎪∂∂∂⎩和关于x 的一维波动方程E H
把,代入无源空间的旋度方程,可得
(,)E x t (,)H x t 0,,0,,y z y y z y z x z y z x x E H E x t E H x H E E x E t H E x t t E t H t
γεγεμγεμμ∂∂=+∂∂∂∂=+∂∂∂=--∂∂∂∂=-∂⎧∂+=⎪⎪∂⎨∂⎪=⎪∂⎩∂∂◆均匀平面电磁波是一横电磁波。
均匀平面电磁波中的电场和磁场都没有和波传播方向相平行的分量。
均和波传播方向相垂直,即对传播方向来说它们是横向的。
这种电磁波称为横电磁波或TEM 波。
E H ◆电场强度和磁场强度的方向和波的传播方向三者相互垂直,且满足右手螺旋关系。
E H
把,代入无源空间的旋度方程,可得
(,)E x t (,)H x t 0,,0,,y z y y z y z x z y z x x E H E x t E H x H E E x E t H E x t t E t H t
γεγεμγεμμ∂∂=+∂∂∂∂=+∂∂∂=--∂∂∂∂=-∂⎧∂+=⎪⎪∂⎨∂⎪=⎪∂⎩∂∂ 分量和构成一组平面波;分量和构成另一组平面波。
这两组分量彼此独立,但电磁波中的合成场强由这两组分量波的有关场强构成。
y E z H z E y H 2222222200z z z y y y H H H x t t E E E x t t μγμεμγμε⎧∂∂∂--=⎪⎪∂∂∂⎨∂∂∂⎪--=⎪∂∂∂⎩2222222200y y y z z z H H H x t t E E E x t t μγμεμγμε⎧∂∂∂--=⎪⎪∂∂∂⎨∂∂∂⎪--=⎪∂∂∂⎩
三、小结
1. 无源空间的电磁波动方程
2. 均匀平面电磁波的一维波动方程
3. 均匀平面电磁波的性质
横电磁波,TEM波
电场、磁场、传播方向满足右手螺旋关系
相互垂直的电场和磁场分量方程相互独立。