2018版大学数学系列课程一览
- 格式:doc
- 大小:38.00 KB
- 文档页数:2

高等数学工本2018教材高等数学是一门综合性的数学科学,广泛应用于自然科学、工程技术和社会科学等领域。
为了提高学生的数学素养,培养他们的逻辑思维和问题解决能力,高等数学工本2018教材被设计为一本全面而系统的教学工具。
本文将对该教材的重要内容进行简要介绍。
一、微积分微积分是高等数学中最重要的分支之一,也是许多其他学科的基础。
在高等数学工本2018教材中,微积分部分详细介绍了函数、极限、导数和积分等概念。
通过理论讲解和实例演示,学生可以逐步掌握微积分的基本操作和应用技巧。
同时,教材还提供了大量的练习题和问题,帮助学生巩固所学知识,并培养他们的解决实际问题的能力。
二、线性代数线性代数是高等数学中的另一门重要分支,它研究向量、矩阵和线性变换等基本概念及其相互关系。
高等数学工本2018教材中的线性代数部分包括向量空间、线性方程组、矩阵分析等内容。
通过理论推导和实例演示,学生可以逐步掌握线性代数的基本理论和常用技巧。
教材还提供了大量的线性代数应用题,帮助学生将学到的知识应用到实际问题中。
三、级数与数学归纳法高等数学工本2018教材中的级数与数学归纳法部分介绍了级数求和、收敛性判断和数学归纳法等重要概念。
通过理论解析和问题讨论,学生可以深入理解级数的性质和应用场景,并掌握数学归纳法的基本思想和操作方法。
教材还提供了一些具有挑战性的问题和练习题,帮助学生提高证明能力和问题解决能力。
四、多元函数与偏导数多元函数与偏导数是高等数学中的另一个重要内容,它研究多元函数的极限、连续性、可微性等性质。
高等数学工本2018教材中的这一部分详细讲解了多元函数的基本概念和重要定理,以及偏导数的定义和计算方法。
通过理论阐述和实例演示,学生可以逐步掌握多元函数与偏导数的相关知识和技巧。
同时,教材还提供了一些综合性的问题和实例,帮助学生将多元函数与偏导数应用于实际问题中。
五、常微分方程常微分方程是高等数学中的一门重要学科,它研究函数的导数与自变量之间的关系。

大学数学课程目录一、基础数学课程1. 高等数学1.1 微积分1.2 数列与级数1.3 多元函数微积分2. 线性代数2.1 矩阵与向量2.2 行列式与矩阵的逆2.3 线性方程组与解空间二、概率与统计1. 概率论与数理统计1.1 概率空间与事件1.2 随机变量与概率分布1.3 参数估计与假设检验三、离散数学1. 图论1.1 图的基本概念1.2 最短路径与最小生成树1.3 匹配与网络流四、数值计算方法1. 数值计算方法1.1 插值与逼近1.2 数值积分与数值解微分方程1.3 线性方程组的数值解法五、数学分析1. 实分析1.1 极限与连续1.2 一元函数微积分1.3 常微分方程六、复变函数1. 复变函数1.1 复变函数与解析函数1.2 留数与积分变换1.3 应用:调和函数与辐角原理七、偏微分方程1. 偏微分方程1.1 一阶与二阶偏微分方程1.2 分离变量法与叠加原理1.3 积分变换法与解析解八、拓扑学1. 拓扑学1.1 拓扑空间与连续映射1.2 连通性与紧致性1.3 定向和同伦等价九、几何学1. 解析几何1.1 空间点、直线与平面1.2 圆锥曲线与二次曲面1.3 空间位置关系与投影几何以上为大学数学课程目录的一个简要概述。
大学数学课程的目标是培养学生的数学思维能力和问题解决能力。
不同课程之间存在一定的联系和依赖,学生可以按照自己的兴趣和发展方向选择适合的课程进行学习。
这些数学课程将为学生日后的学术研究、工程技术和各类应用领域提供坚实的数学基础。
通过大学数学课程的学习,学生将掌握数学的基本概念、方法和技巧,培养逻辑思维和分析问题的能力,为未来的发展打下坚实的基础。

二重积分概念与性质课程思政教学设计邓明香㊀冯永平(广东省广州大学数学与信息科学学院㊀510006)摘㊀要:专业课课程思政要实现 门门课程有思政 ꎬ大学数学公共基础课课程思政的重点在于提高大学生综合素质.本文以数学类公共课程二重积分课堂教学为例ꎬ分析了该课程蕴含的数学思政教育元素ꎬ从教学方法㊁案例设计思路㊁改革目标和实施方案等方面提出了课程思政融入方案ꎬ以潜移默化地提高学生的文化自信ꎬ树立社会主义核心价值观.关键词:二重积分ꎻ课程思政ꎻ案例设计ꎻ教学改革中图分类号:G632㊀㊀㊀文献标识码:A㊀㊀㊀文章编号:1008-0333(2023)03-0047-03收稿日期:2022-10-25作者简介:邓明香(1974-)ꎬ女ꎬ甘肃省秦安人ꎬ硕士ꎬ讲师ꎬ从事微分方程数值解的研究.冯永平(1975-)ꎬ男ꎬ甘肃省甘谷人ꎬ博士ꎬ教授ꎬ从事微分方程数值解的研究.基金项目:线性代数 课程思政 教学的探索与实践(2020年教育部产学合作协同育人项目202002140010)ꎻ高等数学Ⅱ 课程思政 教学的探索与实践(2020广东省本科高校教学质量与教学改革工程项目ꎬ粤教高函ʌ2020ɔ20号)ꎻ经管类微积分课程翻转课堂教学模式研究(高等学校大学数学教学研究与发展中心教学改革项目CMC20200216)ꎻ新时代大学数学课程群教研室(2021广东省本科高校教学质量与教学改革工程项目ꎬ粤教高函ʌ2021ɔ29号).㊀㊀二重积分是多元函数微积分学应用的一个主要内容ꎬ是在解决实际问题的实践中不断抽象出来的ꎬ是一元函数定积分㊁多元函数曲线积分的推广.结合课程思政相关元素ꎬ本文主要从学情分析㊁教学目标㊁教学方法㊁教学策略㊁教学设计几方面探讨了二重积分的概念教学中如何隐性地融入课程思政元素ꎬ达到教书育人的目的.1学情分析及教学目标分析本节课程选自理工类专业必修课«高等数学Ⅱ2»ꎬ为一节新授课程ꎬ第8章«二重积分»第1节 二重积分的概念与性质 ꎬ教材选用林伟初ꎬ郭安学ꎬ高等数学(经管类下册ꎬ第1版)ꎬ北京大学出版社ꎬ2018.07ꎬ面向我校一流专业地理科学专业211㊁212㊁213班开设.本节课程学习前ꎬ学生已掌握了一些规则立体图形的体积求法ꎬ如长方体㊁圆柱体㊁锥体等ꎻ已学完一元微积分学㊁空间解析几何及多元函数的微分学等高等数学内容ꎻ掌握了定积分概念及相关数学思想ꎬ能熟练使用分割㊁近似㊁求和㊁取极限四个步骤求解曲边梯形面积问题.在学习中ꎬ学生对推广后的求解曲顶柱体体积问题能给出粗略方案ꎬ但精确化比较困难ꎬ特别是对最后如何从近似转向精确的极限手法难以理解ꎻ学生对概念中涉及的积分区域和重积分符号的抽象性和复杂性有畏惧感ꎬ容易排斥抽象的概念课.本节课程的教学目标为以下几个方面.知识与能力方面:掌握二重积分的概念㊁性质ꎻ学会用极限思想分析具体问题ꎬ能灵活使用 分割ꎬ近似ꎬ求和ꎬ取极限 处理二元函数的相关74问题ꎻ掌握从实例形成概念定义的重要方法.过程与方法方面:通过类比定积分ꎬ引导学生回顾 以直代曲 在解决定积分问题中起到的关键作用ꎬ为整节课架设一个基本思维框架ꎬ让学生明确学习内容ꎻ借助熟悉的 顶面为平面的体积计算问题 密度均匀分布平面薄片质量计算问题 ꎬ引导学生学会从特殊到一般ꎬ从具体到抽象的数学方法ꎬ实现能力目标的培养.情感方面:借助引例直观体会 以直代曲 和 逼近 的思想ꎬ学习归纳㊁类比的推理方式ꎬ体验从特殊到一般㊁从具体到抽象㊁化归与转化的数学思想ꎻ从实践中创设情境ꎬ渗透 化整为零㊁积零为整 的辨证唯物观ꎬ培养学生的创新意识和科技服务于生活的人文精神.本课程用 问题驱动 教学理念的统领指导实施课程教学ꎬ力求在课程教学中实现培养学生具备 用数学的眼光观察世界ꎬ用数学的思维分析世界ꎬ用数学的语言表达实现世界 的最终能力素养目标.㊀2教学过程教学过程教学环节教师活动学生活动设计意图及思政融入Ⅰ.问题引入及问题分析(10分钟)图11.引例1:曲顶柱体的体积问题:回忆柱体与长方体的体积计算ң变平面为曲面ꎬ引出新问题ң回顾微积分数学史及定积分ꎬ启发学生寻找思路ң视频动态演示求解思路ꎬ让学生有直观认识(如图1).2.引例2:平面薄板质量求解问题:回顾均匀密度下平面薄板质量计算公式ң类比引例1过程ꎬ给出一般方法.3.引例分析:比较总结两个引例思想方法㊁过程与结构式ң提炼共性ң形成定义.1.回答问题(基本知识ꎬ学生纷纷举手)ꎻ2.思考新问题(有些疑虑)ꎻ3.参与互动ꎬ积极总结情景-问题教学ꎬ启发学生思考三个问题ꎬ逐层推进ꎬ逐步深入ꎬ使学生充分认识到用小平顶柱体近似代替小曲顶柱体的合理性ꎬ实现由感性认识到理性认识的升华.实例引入ꎬ激发学生兴趣ꎬ调动学生自行探索ꎬ自然发现问题.视频演示求曲顶柱体体积过程ꎬ形象地展示 分割㊁近似替代㊁求和㊁取极限 的经典过程ꎬ让学生直观理解解决问题的基本思想ꎬ明确其正确性和可执行性ꎬ增强学习信心.通过图示ꎬ引导学生对引例进行类比ꎬ有益于快速观察到要点ꎬ有助于形成初步印象.Ⅱ.讲授及探讨概念(15分钟)1.ppt展示二重积分定义ꎬ分步强调关键表述ꎻ2.与定积分进行类比:列表类比ң概念形成数学思想和过程ң二重积分的几何性质和物理意义ң二重积分的发展简史.1.概念讲授时主要以聆听为主ꎻ2.类比中尝试学生自己进行总结ꎬ再对照加深理解.强调这是重点:1.从多个方面进行深入探讨ꎬ加深概念理解.2.积分数学思想ꎻ3.相关的数学发展史简介ꎬ拓展知识视野ꎻⅢ.巩固知识与强化拓展(15分钟)例1㊀利用二重积分定义计算∬[0ꎬ1ꎻ0ꎬ1]x2ydσꎻ讨论㊁练习板书讲解ꎬ巩固概念及性质ꎬ感知利用概念计算二重积分的困难性.培养学生求真求实㊁踏实认真的做事态度.84Ⅳ.思想方法与知识总结(3分钟)Ⅴ.课后作业布置及预习(2分钟)1.作业:课后习题1ꎬ6ꎻ2.小组任务:思维导图制作(提示:知识结构㊁与定积分类比㊁思想方法等)3.预习:二重积分的计算.教学评价与反思1.在教学理念方面:课程以学生为中心ꎬ为学生创设学习的情境ꎬ让学生在课堂上成为主角ꎬ教师转变为学习的组织者㊁引导者㊁合作者.2.在知识目标方面:做到教学思路清晰㊁突出重点㊁突破难点.3.在教学过程方面:在课堂上采取小组讨论㊁个别提问㊁学生总结等方法让学生参与到教学过程中ꎬ让学生感悟数学方法ꎬ立德树人ꎬ突出能力培养ꎬ关注学生的终身发展.4.在教学方法与策略方面:能根据教学目标㊁教学内容选择合适的教学方法.板书设计21.1.二重积分的概念及其存在性一㊁二重积分的引入:(1)曲顶柱体的体积ꎻ(2)平面薄片物体的质量二㊁二重积分的概念:(1)二重积分的概念ꎻ(2)概念包含的数学思想ꎻ(3)概念的几点注解ꎻ(4)二重积分的几何㊁物理意义三㊁二重积分应用例题例1㊀利用二重积分定义计算∬[0ꎬ1ꎻ0ꎬ1]x2ydσꎻ课程资源1.参考资料(1)菲赫金哥尔茨ꎬ微积分学教程ꎬ人民教育出版社ꎬ2006.01.(2)朱健民ꎬ李建平ꎬ«高等数学»(第二版)上册ꎬ高等教育出版社ꎬ2015年.(3)詹姆斯 斯图尔特ꎬ«微积分»(第六版)ꎬ中国人民大学出版社ꎬ2014年.2.课程团队与教学资源(1)2019年5月成立了 大学数学 教学团队ꎻ(2)2010-至今的课程教学大纲㊁年度教学进度表㊁试题库ꎻ(3)2021年团队获评广州大学黄大年式培育教师团队ꎻ参考文献:[1]康瑞妮.问题驱动型二重积分概念的教学设计研究[J].教师ꎬ2021(29):31-32.[2]雍龙泉.直角坐标系下二重积分的计算方法研究[J].湖北工程学院学报ꎬ2019ꎬ39(06):106-108.[3]曹剑成. 以学定教 模式的研究 以 二重积分 为例[J].理科爱好者(教育教学)ꎬ2020(06):3-4.[4]彭东海ꎬ张留伟.二重积分方法在定积分计算与证明中的应用[J].高等数学研究ꎬ2021ꎬ24(02):35-37.[5]申爱红ꎬ孙文娟.新时代背景下«高等数学»课程教学的提质与创新[J].沈阳师范大学学报(自然科学版)ꎬ2021ꎬ39(01):80-84.[6]杨慧卿.积分学教学研究与实践[J].高等数学研究ꎬ2021ꎬ24(02):58-61.[责任编辑:李㊀璟]94。

目录一、理论物理一月特训班二、本科数学一月特训班三、西方哲学一月特训班四、零基础突破日语N5一月特训班五、经济金融一月特训班六、2018考研冲刺预测一月特训班七、Python零基础特训班八、实用数据挖掘与人工智能一月特训班九、人工智能、大数据与复杂系统一月特训班十、CFA LEVEL I一月特训班十一、零基础实用留学德语一月特训班十二、程序员成长攻略零基础特训班十三、2018CPA一月特训班十四、法语零基础一月特训班十五、GRE核心词汇3000故事串讲十六、分析化学精讲十七、2018年公务员考试联考/省考一月特训班十八、JavaScript零基础进阶班十九、解密机器学习中的监督学习二十、微软办公软件国际认证二十一、数据结构与算法进阶班二十二、2018年一级注册建筑师全面攻破二十三、12小时学会搭建电商平台二十四、实现财富自由的科学路径——量化投资二十五、零基础也能学量化——量化投资一月特训班二十六、计算机科学一月特训班二十七、BEC商务英语一月特训班二十八、Java零基础特训班二十九、征服老板:零基础做出高逼格PPT三十、微信小程序实战开发特训班三十一、《线性代数》期末考试5日通关班三十二、机械设计制造及自动化一月特训班三十三、HTML5+CSS3零基础特训班三十四、Android开发零基础特训班三十五、AJAX+JQuery实战提高特训班三十六、本科物理一月特训班三十七、国家法律职业资格考试特训班三十八、2019年国家公务员考试一月特训班一、理论物理一月特训班1.【课程名称】理论物理一月特训班2.【课程简介】本科物理重点难点一次搞定!一生一次的人生挑战!课程完整覆盖物理系本科所有核心内容:高等数学、线性代数、复变函数、数学物理方程、理论力学、量子力学、电动力学、热力学与统计物理、微分几何、广义相对论、量子电动力学等,细分的给力知识点,完整的全局观呈现,一次性统统学会!3.【老师简介】童哲,万门大学校长。

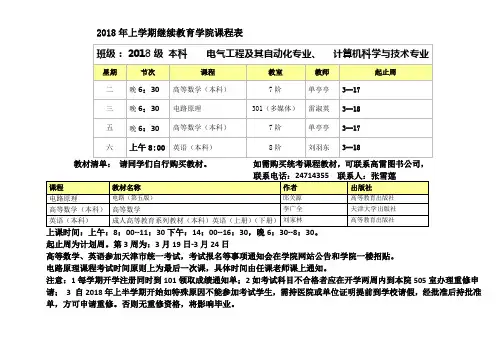
2018年上学期继续教育学院课程表教材清单:请同学们自行购买教材。
如需购买统考课程教材,可联系高雷图书公司,上课时间:上午:8:00--11:30下午:14:00--16:30,晚6:30--8:30。
起止周为计划周。
第3周为:3月19日-3月24日高等数学、英语参加天津市统一考试,考试报名等事项通知会在学院网站公告和学院一楼招贴。
电路原理课程考试时间原则上为最后一次课,具体时间由任课老师课上通知。
注意:1每学期开学注册同时到101领取成绩通知单;2如考试科目不合格者应在开学两周内到本院505室办理重修申请;3 自2018年上半学期开始如特殊原因不能参加考试学生,需持医院或单位证明提前到学校请假,经批准后持批准单,方可申请重修。
否则无重修资格,将影响毕业。
2018年上学期继续教育学院课程表教材清单:请同学们自行购买教材。
如需购买统考课程教材,可联系高雷图书上课时间:上午:8:00--11:30,晚6:30--8:30,起止周为计划周。
第3周为:3月19日-3月24日高等数学、英语参加天津市统一考试,考试报名等事项通知会在学院网站公告和学院一楼招贴。
会计学基础课程考试时间原则上为最后一次课,具体时间由任课老师课上通知。
注意:1每学期开学注册同时到101领取成绩通知单;2如考试科目不合格者应在开学两周内到本院505室办理重修申请;3 自2018年上半学期开始如特殊原因不能参加考试学生,需持医院或单位证明提前到学校请假,经批准后持批准单,方可申请重修。
否则无重修资格,将影响毕业。
2018年上学期继续教育学院课程表教材清单:请同学们自行购买教材。
如需购买统考课程教材,可联系高雷图书上课时间:上午:8:00--11:30,晚6:30--8:30,起止周为计划周。
第3周为:3月19日-3月24日高等数学、英语参加天津市统一考试,考试报名等事项通知会在学院网站公告和学院一楼招贴。
工程图学及计算机绘图课程考试时间原则上为最后一次课,具体时间由任课老师课上通知。
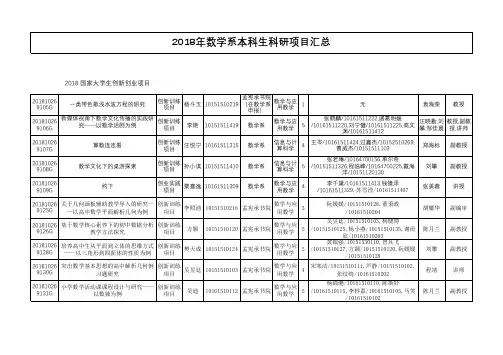
2018 国家大学生创新创业项目201810269105G一类带色散浅水波方程的研究创新训练项目杨斗玉10151510219孟宪承书院(在数学系申报)数学与应用数学1无袁海荣教授20181026 9106G 新媒体视角下数学文化传播的实践研究——以数学话剧为例创新训练项目李艳10151511419数学系数学与应用数学5张鹤麟/10161511222,诸葛明媛/10161511220,刘宁健/10161511225,高文渊/10161511412汪晓勤,刘攀,邹佳晨教授,副教授,讲师201810269107G算数连连看创新训练项目汪悦宁10161511315数学系信息与计算科学4王岑/10161511424,过鑫杰/10152510269,曹威杰/10151511103郑海标副教授201810269108G数学文化下的桌游探索创新训练项目孙小淇10151511410数学系信息与计算科学5张若琳/10164700156,单尔奇/10151511326,程临峰/10164700225,戴海洋/10151120130刘攀副教授201810269109G约下创业实践项目粟嘉逸10161511309数学系数学与应用数学4李千黛/10161511413,钱镜泽/10161511329,苏雪滢/10161511407张美蓉讲授20181026 9125G 关于几何画板辅助教学导入的研究——以高中数学平面解析几何为例创新训练项目李照清10151510216孟宪承书院数学与应用数学3阮媛媛/10151510128,董秉政/10161510204胡耀华副编审20181026 9126G 基于数学核心素养下的初中数据分析教学方法探究创新训练项目方颖10151510120孟宪承书院数学与应用数学5吴昱廷/10151510103,杨晓博/10151510125,杨小燕/10151510135,谢雨欣/10161510203陈月兰副教授20181026 9128G 培养高中生从平面到立体的思维方式——以三角形到四面体的性质为例创新训练项目樊天成10151510124孟宪承书院数学与应用数学5黄银强/10151530110,曾凡飞/10151510127,方颖/10151510120,阮媛媛/10151510128刘攀副教授20181026 9130G 突出数学基本思想的高中解析几何例习题研究创新训练项目吴昱廷10151510103孟宪承书院数学与应用数学4宋寒洁/10151510111,芦静/10151510102,张纹绮/10161510202程靖讲师20181026 9131G 小学数学活动课课程设计与研究——以数独为例创新训练项目吴迪10161510112孟宪承书院数学与应用数学5杨锦滟/10161510110,陈斯妤/10161510115,李杪嘉/10161510105,马笑/10161510102陈月兰副教授2018年数学系本科生科研项目汇总2018 上海市大学生创新创业项目201810269104S校园脉创业实践项目李千黛10161511413数学系数学与应用数学3王清帅/10152510128, 华赟/10152510157羊丹平教授20181026 9105S 跨学科教育——将古算诗词等融入到小学数学教育中的延伸与扩展创新训练项目刘沁怡10161511431数学系信息与计算科学6王云鲲/10165301117,王玉昭/10165301213,吴雅晴/10171510203,覃月娇/10171510219,管一锦/10171511304杜荣教授20181026 9106S 综合分析女性数学家为数学推进的重要意义创新训练项目刘宗钰10151511335数学系信息与计算科学4林雪飞/10140340143,刘莹/10151511208,宋利/10154507106刘攀副教授201810269107S华师大代金券交易平台创业实践项目苏雪滢10161511407数学系数学与应用数学5卢洁卉/10161511304,张家栋/10161511430,王春月/10161511402,陈珊珊/10161511106陆俊副教授201810269108S“一起”地图式聊天软件开发创业实践项目郑淦心10161511209数学系数学与应用数学3林雪飞/10140340143,季真俊/10142510142郑海标副教授20181026 9124S 大学数学与高中数学的脱节问题与衔接研究创新训练项目季海霞10161510212孟宪承书院数学与应用数学5翁婷/10161510214,郑静/10165301102,杨玉玲/10161510207,蓝怡/10161510116吴瑞聪研究员20181026 9126S 基于核心素养的高中数学活动课案例开发与实践——以“数学抽象”、“逻辑推理”为例创新训练项目蒋铖昊10151510107孟宪承书院数学与应用数学5孙英博/10151510106,杨芳/10151510110,甯彭林/10151510109,杨锦滟/10161510110鲍建生教授20181026 9127S 基于教学视频分析的职前数学教师发展研究创新训练项目李龙章10151510226孟宪承书院数学与应用数学5陈慧慧/10151510229,郭鸣俊/10141530116,沈鸿宇/10151510227,刘春华程靖讲师20181026 9130S 指向高中数学课堂教学的建模素养研究——以导入为例创新训练项目齐小娟10151510115孟宪承书院数学与应用数学5朱艳慧/10151510118,卢月/10151510131,杨斗玉/10151510219,杨玉玲/10161510207陈月兰副教授2018 校级大学生创新创业项目201810269218X光滑三次曲面上的27条直线创新训练项目张颖婕10151511432数学系信息与计算科学3金雨波/10161511215,沈超/10152150130杜荣教授201810269219X用纯实矩阵研究复分析中的问题创新训练项目付君纳10151511330数学系数学与应用数学3乐哲君/10151511325,王恃铁/10175300113吴瑞聪研究员201810269220X勇者拉提斯创业实践项目季真俊10142510142数学系数学与应用数学2潘博隆/10151511108郑海标副教授201810269221X基于数学背景的数学讨论研究提高班创新训练项目张晋新10161511104数学系数学与应用数学2苏雪滢/10161511407温玉亮副教授20181026 9222X 利用自然语言处理等方法对奥赛试题进行自动分类创新训练项目张子新10151511231数学系数学与应用数学5张瑞/10151511429,孙小淇/10151511410,杨洪鑫/10151511202,肖遥志/10151511431焦翔宇副教授20181026 9223X 基于数学核心素养的高中数学建模案例开发和实践创新训练项目诸静娴10151510207孟宪承书院(在数学系申报)数学与应用数学5顾彦知/10151510205,王悦文/10151510104,冯斌/10140340123,沈思毓/10161510219鲍建生教授20181026 9224X 基于数学建模优化EVCARD分时租赁系统——以上海市EVCARD模式为例创新训练项目徐雯珺10154601158孟宪承书院(在数学系申报)数学与应用数学5刘斯琪/10161510208,陈永昌/10151510121,王资伟/10161510223,郭红红/10161510109万福永副教授201810269256X辅助线在初等几何论证中的应用创新训练项目沈佳伟10151530116孟宪承书院数学与应用数学5陈永昌/10151510121,刘兵/10151510130,刘峻浩/10161510111,刘斯琪/10161510208温玉亮副教授20181026 9259X 关于小学高年级学生几何学习困难的个案研究创新训练项目李亚琦10151510214孟宪承书院数学与应用数学5张文君/10151510105,沈祥雨/10151510225,赵伦楷/10171510104,申皓雪/10161510209程靖讲师20181026 9267X 全国高考统一命题背景下各省的应对情况反馈和应对措施分析--以山西、重庆、福建、宁夏的数学教育为例创新训练项目郭红红10161510109孟宪承书院数学与应用数学5谭倩/10161510119,叶慧琼/10161510104,张佩泽/10165301111,杨蓉/10165301108吴颖康副教授。

机械工程学院中文
1.工程知识(专业
知识)
验证性实验
理论课(不含实践环
节)
化工学院英文 2.问题分析综合性实验理论课(含实践环
节)
电子工程
与光电技术学院法文
3.设计/开发解决
方案(解决方案制
定)
设计性实验实验课
计算机科
学与技术
学院
4.研究研究创新性实验毕业设计(论文)经济管理
学院
5.使用现代工具操作性实验科研训练
能源与动力工程学院6.工程与社会(实
践与社会)
演示性实验校内实习
自动化学院7.环境和可持续
发展
校外实习
理学院8.职业规范学年论文/社会调查外国语学
院
9.个人和团队课程设计/综合实验公共事务
学院
10.沟通军事体育类
材料科学
与工程学
院
11.项目管理
环境与生
物工程学
院
12.终身学习
设计艺术
与传媒学
院
教育实验
学院
知识产权
学院
马克思主
义学院
国际教育
学院
工程训练
中心
中法工程
师学院
宣传部
教务处
学生工作
处
研究生院
团委
高等教育
研究所
国际交流
合作处
军工试验
中心
军区培养办公室南中医南理工班体育部图书馆文化艺术素质教育中心
现代教育技术中心校医院外单位。

地方师范院校由于受生源质量、师资水平等各方面条件的限制,数学专业毕业生主要去地方中小学担任数学教师,所以很多数学专业学生对大学数学课程的重要性认识不够,抱着应付过关的态度,对每门专业数学课程的学习都是“蜻蜓点水”浅尝辄止,对各门数学课程之间的联系鲜少思考,这导致学生所学的大学数学知识是零散的,孤立的。
但是,数学专业的数学课程是一个完整的体系,互相之间联系紧密,学生不仅要掌握每门专业课程,更要思考和掌握各门课程之间的联系,这样才能真正掌握数学学科的基本理论、基本知识与基本方法,才能运用所学的数学知识解决实际问题。
《抽象代数》被认为是大学数学的新“三基”之一,它研究群、环、域等代数体系,是经典代数知识的抽象和深化,具有严密的逻辑性和高度的抽象概括性,学生必须跟上教师的授课进度消化每节课的内容并将已学的知识点连贯起来,才能理解后续的教学内容。
由于授课学时有限,每节课的授课内容多,教师在课堂上一般按照例子、定义、定理的模式讲解,学生被动地接受知识灌输;很多同学对于该课程的重要性认识不够,甚至认为该课程“无用”,课程内容又抽象难懂,因此学习该课程时不积极主动,甚至有厌学情绪,不仅没法掌握基本的知识与方法,更谈不上利用抽象代数的相关知识和方法解决实际问题。
事实上,抽象代数不仅能培养学生的抽象思维能力,更为解决很多实际问题提供了方法。
比如,伽罗瓦在1832年运用“群”的概念彻底解决了用根式求解代数方程的可能性问题。
此外,抽象代数还与其它的数学专业课程联系紧密,或为其它课程提供了理论基础,或者其它一些课程可提供抽象代数的具体例子,而抽象代数的相关概念是这些例子的高度抽象,比如高等代数知识为《抽象代数》提供了很多具体的模型[1]。
因此,要充分挖掘该课程的重要意义及其与其它数学课程的联系,利用第二课堂和课堂教学时间见缝插针帮助学生理解、巩固所学知识。
本文将从具体的实例入手,帮助学生充分认识《抽象代数》的重要性,分析《抽象代数》与《复变函数》《实变函数》等课程之间的联系,进一步理解抽象代数理论。
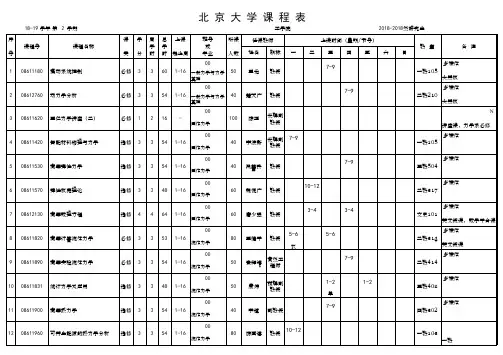
电子科技大学2017-2018学年第一学期研究生课程表2017年9月4日(校历第一周周一)起执行研究生院二〇一七年七月目录课程表说明 (Ⅰ)电子科技大学2017-2018学年校历 (Ⅶ)研究生上课时间表 (Ⅷ)清水河校区课程表 (1)沙河校区课程表 (20)同一班次研究生课程由多位教师上课学时周次分配表 (28)学科前沿知识专题讲座登记表 (36)课程表说明一、开课时间前10周开课的课程从2017年9月4日(校历第一周周一)起正式上课。
后10周开课的课程从2017年11月13日(校历第十一周周一)起正式上课。
二、选课说明所有研究生课程全部实行网上选课。
前十周所开课程可试听一周,并于校历第一周进行网上选课;后十周所开课程也可试听一周,并于校历第十一周进行网上选课。
具体选课时间及选课规则请密切注意研究生院网站()通知。
三、编班说明1、中国特色社会主义理论与实践(16005004)共开设17个班,每班限选260人,其中清水河校区开设13个班,沙河校区开设4个班。
2、硕士研究生学位英语(13005015)共开设69个班,每班限选60人。
本学期两校区开设A级班、B级班、C级班;清水河校区共52个班,其中A级实验班14个、B 级班37个、C级班1个;沙河校区共17个班,其中A级实验班5个、B级班11个、C级班1个。
3、工程伦理与学术道德(11005001)共开设7个班,每班限选100人,其中清水河校区开设5个班,沙河校区开设2个班。
4、知识产权与信息检索(11005002)共开设4个班,每班限选100人,其中清水河校区开设3个班,沙河校区开设1个班。
5、数学基础课分班:矩阵理论(10005001)共开设15个班,每班限选160人,其中清水河校区开设12个班,沙河校区开设3个班。
随机过程及应用(20005001)共开设12个班,每班限选160人,其中清水河校区开设11个班,沙河校区开设1个班。
数学物理方程与特殊函数(10005004)共开设7个班,每班限选160人,其中清水河校区开设4个班,沙河校区开设3个班。
高等数学2018版教材高等数学是大学理工科学生必修的一门重要课程,也是数学学科中的一门核心课程。
它主要涉及微积分、线性代数和概率论等内容,为学生打下扎实的数学基础,为未来的学习和科研工作奠定良好的基础。
2018版的高等数学教材以全新的理论和实例展示了数学的美妙与应用,本文将从教材的主要内容、特点和应用等方面进行论述。
一、教材主要内容2018版的高等数学教材包括微积分、线性代数和概率论这三个主要模块。
微积分模块主要包括导数与微分、积分与定积分以及微分方程等内容。
线性代数模块则涉及向量与矩阵、线性方程组、特征值与特征向量等内容。
概率论模块则引入了基本概念、随机事件、概率分布以及统计推断等内容。
这些内容相互关联,构成了高等数学教材的核心。
二、教材特点2018版的高等数学教材具有以下特点:1. 理论与实例相结合:教材在讲解理论的同时,注重使用实例来说明与应用,使学生能够更好地理解和掌握知识点。
2. 知识的逻辑性和系统性:教材按照知识点的逻辑顺序进行组织,层层递进,使学生能够循序渐进地学习高等数学的知识。
3. 强调实际应用:教材注重将高等数学理论与实际应用相结合,通过真实场景的案例分析,让学生了解数学在实际问题中的应用和意义。
4. 提供丰富的习题和案例:教材提供了大量的习题和案例,供学生进行练习和巩固知识。
这些习题覆盖了各个难度级别,有助于学生提高解题能力。
三、教材应用高等数学教材的应用范围非常广泛。
首先,在学术领域中,高等数学是许多理工科学科的基础,如物理学、化学、力学等。
它们在研究领域中需要运用微积分、线性代数和概率论等数学方法进行建模和分析。
其次,在工程领域中,高等数学也扮演着重要的角色。
例如,在电路设计和信号处理中,需要运用微积分和线性代数的知识。
最后,在日常生活中,高等数学也有许多应用。
比如,金融领域的投资分析、医学领域的生物统计等,都需要高等数学的支持。
总之,高等数学2018版教材以其全新的理论和实例,准确地满足了学生的内容需求。
信息与计算科学专业本科人才培养方案(2018版)一、培养目标培养德、智、体全面发展,具有扎实的数学基础,掌握信息与计算科学基本理论和方法,受到科学研究和专业技能训练,能够运用所学知识解决信息和工程计算领域的一些实际问题,能在科技、教育和经济等部门从事研究、教学、应用开发及管理工作的复合型专门人才。
二、培养要求1. 热爱中国共产党,热爱社会主义祖国,积极践行社会主义核心价值观;具有爱岗敬业、艰苦奋斗、热爱劳动、遵纪守法、团结合作的优秀品质;热爱信息与计算相关行业工作。
2. 具有扎实的数学基础,掌握信息科学和计算科学的基本理论与基本知识,具备在本专业领域从事科学研究、软件开发、信息处理及计算编程的能力,能用所学知识解决一些实际问题。
3. 掌握文献检索、资料查询的基本方法,具有了解信息与计算科学领域新成果的能力。
掌握一门外语,能够较顺利地阅读本专业的外文书刊。
4. 具有健康的体魄和一定的军事基本理论和技能,养成良好的体育锻炼和卫生习惯,达到国家规定的大学生体育合格标准。
三、专业主干课程数学分析,高等代数,解析几何,常微分方程,概率论,数理统计,离散数学,点集拓扑,计算方法,C语言程序设计,信息论基础,运筹学。
四、学制与学位学制:基本学制4年,实行3—6年弹性学制授予学位:理学学士学位五、课程结构周课时六、教学计划表完成一次实践调查并提交调查报告或完成一篇学术论文(3000字以上);2. 参加院级及以上的文体比赛/学科知识技能竞赛并成功参赛,或参加大学生科技创新项目并结题。
3. 1-3学年每学年参加四次以上学术活动(报告、讲座等)。
七、通识选修课程学分要求八、专业主干课程简介1.课程名称:数学分析(Mathematical Analysis)(1)课程代码:Z3804001, Z3804007, Z3804014(2)课程简介:数学分析是专业核心课程,是微分几何、微分方程、复变函数、实变函数、泛函分析等课程必备的基础。
湖北大学本科教学课程体系与学分要求一、课程结构体系湖北大学2018版本科人才培养方案实施“平台+模块”的课程结构体系,该体系由通识教育课程平台、学科大类课程平台、专业核心课程平台、专业方向课程平台、集中实践教学环节和课外创新实践活动构成,各部分内容及学分要求见表1-表3。
(一)通识教育课程平台通识课程包括通识必修课程和通识选修课程。
通识必修课程36学分。
包括思想政治课程群(16学分)、大学体育课程群(4学分)、大学英语课程群(10学分)、计算机基础课程(2学分)、大学生心理健康教育课程(2学分)、创新创业理论课程(2学分)。
通识选修课程6学分(其中认证专业为4学分)。
包括科学精神与科学技术、社会发展与公民教育、人文经典与人生修养、艺术鉴赏与审美人生四大课程模块。
通识选修课程旨在培养学生人文情怀、科学素养、批判思维、沟通表达、广博视野,使学生全面理解人类社会及科学技术的发展规律,掌握各类学科的基础知识与技能,形成均衡的知识结构,获得必要的能力训练,具备创新创业意识等综合素质。
(二)学科大类课程平台学校实行按大类和专业培养相结合的培养模式,2018年新增专业大类8个,包含22个专业;2018年撤销服装与服饰设计和自然地理与资源环境专业。
停招电子商务及法律和环境科学专业,共计招生专业大类(专业)40个,其中以专业大类招生17个(包含55个专业),单独招生专业23个。
学科大类平台类的学科基础课程根据各大类和专业的具体情况设置25-31学分,包括学科基础课程(必修)(21-25学分)、学科基础选修课程(根据学科大类或专业的需要设置专业引导性课程)(选修)(4-6学分)。
(三)专业核心课程平台与专业方向课程平台专业核心课程平台的课程应根据教育部《普通高等学校本科专业类教学质量国家标准》、《普通高等学校本科专业目录和专业介绍(2012年)》中的主干学科、核心课程、主要实践性教学环节、主要专业实验等有关规定设置。
《应用数学》课程标准一、课程基本信息课程代码:1125学分:4学时:52适用专业:工科类各专业开设学期:2018-2019学年第一学期课程类型: 公共基础课前导课程:高中数学课程或中专、职高同等数学课程后续课程:电工电子技术等二、课程简介课程的性质:高职高专工科类各专业必修的一门公共基础课。
课程的任务:根据高职高专人才培养模式,充分体现高职教育的特点和人才培养目标,符合实践工作中对高职学生应有的基本知识和基本技能的要求,在教学内容与课程体系上,不严格追求数学学科的完整性,将内容进行模块化整合,形成由简单到复杂,突出其应用性,注重对学生分析问题和解决问题能力的培养,以专业培养目标为前提构成的数学课程体系。
本课程内容主要包括:极限与连续、一元函数导数与微分及其应用、一元函数积分及其应用。
通过本课程的学习,可帮助学生完成基本素质的培养,提供高职高专工科类各专业所需的数学知识学习和职业素养,培养高职学生可持续发展需要的能力等。
三、课程教学目标1.能力目标(1)通过本课程学习,学生能逐步理解职业教育的特点,增强职业意识及职业能力的自我意识;(2)能用数形结合的方法解决一些数学及其它相关问题;(3)培养学生抽象思维和逻辑思维的能力,能对生活或工作中的一些问题理性、逻辑地思考并解决;(4)能将一些文字语言转化为数学语言并进行处理;(5)能利用代数式变形等基本方法和技巧解决、处理一些问题;(6)能用数学符号来表达某种思想或想法;(7)能提高学生的数学思维能力;(8)将能一些数学知识融入专业并解决相应问题;(9)能应用所学的数学知识综合分析某些问题,并能解决一些简单的实际问题。
(10)能为后续的专业课程打下必要的数学基础。
2.知识目标(1)理解一元函数建模、极限、微分与积分的思想;(2)理解函数的概念,掌握基本初等函数的常用性质;(3)理解函数的极限、连续性、无穷小与无穷大的概念,掌握连续性及无穷小的性质;(4)掌握求函数极限的基本方法和简单应用;(5)理解导数、微分的概念以及导数的几何意义;(6)掌握求函数导数和微分的基本方法;(7)能利用微分作一些简单的近似计算;(8)理解函数极值的概念;(9)掌握求函数的极值、最值、单调性、凹凸性的方法;(10)掌握简单的实际问题中最值的应用;(11)理解定积分的概念,掌握定积分的几何意义;(12)理解原函数与不定积分的概念;(13)掌握求函数积分的基本方法;(14)掌握利用定积分求平面图形的面积。
2018版鲁东大学大学数学系列课程课程号
由于理工科、经管类学生层次水平要求不同,因此,建议选择课程号时参考以下标准:
1.理科类专业,使用上表中的课程号;
2.工科类专业,将上表中的对应课程号中的第8位改为3,其他数字不变。
比如,交通学院如果选择高等数学A1,课程号应改为:212018131,如果选择高等数学B1,课程号应改为21201813
3.其他课程做类似修改。
(复变函数与积分变换,信息与电气工程学院用212018111课程号,蔚山与海洋学院用212018121课程号)3.经管类专业,将上表中的对应课程号中的第8位改为4,其他数字不变。
其他操作办法同2.
4.文科类专业,将上表中的对应课程号中的第8位改为5,其他数字不变。
其他操作办法同2.
5.社科类专业,将上表中的对应课程号中的第8位改为6,其他数字不变。
其他操作办法同2.
6.中外合作办学专业,将上表中的对应课程号中的第8位改为7,其他数字不变。
其他操作办法同2.
7.校企合作专业,将上表中的对应课程号中的第8位改为8,其他数字不变。
其他操作办法同2.
8. 专科专业,将上表中的对应课程号中的第8位改为9,其他数字不变。
其他操作办法同2.
注:如果一个专业既是理科专业,又是中外合作办学专业,应选择中外合作办学专业,其他情况类似。
如再有特殊情况,请与数学与统计科学学院联系。