3.2 动量算符和角动量算符
- 格式:ppt
- 大小:287.50 KB
- 文档页数:24


第三章 力学量用算符表达§3.1 算符的运算规则一、算符的定义:算符代表对波函数进行某种运算或变换的符号。
ˆAuv = 表示Â把函数u 变成 v , Â就是这种变换的算符。
为强调算符的特点,常常在算符的符号上方加一个“^”号。
但在不会引起误解的地方,也常把“^”略去。
二、算符的一般特性 1、线性算符满足如下运算规律的算符Â,称为线性算符11221122ˆˆˆ()A c c c A c A ψψψψ+=+ 其中c 1, c 2是任意复常数,ψ1, ψ2是任意两个波函数。
例如:动量算符ˆpi =-∇, 单位算符I 是线性算符。
2、算符相等若两个算符Â、ˆB对体系的任何波函数的运算结果都相同,即ˆˆA B ψψ=,则算符Â和算符ˆB 相等记为ˆˆAB =。
3、算符之和若两个算符Â、ˆB对体系的任何波函数有:ˆˆˆˆˆ()A B A B C ψψψψ+=+=,则ˆˆˆA B C +=称为算符之和。
ˆˆˆˆAB B A +=+,ˆˆˆˆˆˆ()()A BC A B C ++=++ 4、算符之积算符Â与ˆB之积,记为ˆˆAB ,定义为 ˆˆˆˆ()()ABA B ψψ=ˆC ψ= 是任意波函数。
一般来说算符之积不满足交换律,即ˆˆˆˆABBA ≠。
5、对易关系若ˆˆˆˆABBA ≠,则称Â与ˆB 不对易。
若A B B Aˆˆˆˆ=,则称Â与ˆB 对易。
若算符满足ˆˆˆˆABBA =-, 则称ˆA 和ˆB 反对易。
例如:算符x , ˆx pi x∂=-∂不对易证明:(1) ˆ()x xpx i x ψψ∂=-∂i x x ψ∂=-∂ (2) ˆ()x px i x x ψψ∂=-∂i i x xψψ∂=--∂ 显然二者结果不相等,所以:ˆˆx x xpp x ≠ ˆˆ()x x xpp x i ψψ-= 因为是体系的任意波函数,所以ˆˆx x xpp x i -= 对易关系 同理可证其它坐标算符与共轭动量满足ˆˆy y ypp y i -=,ˆˆz z zp p z i -= 但是坐标算符与其非共轭动量对易,各动量之间相互对易。

角动量算符平方与动量分量的对易关系角动量算符和动量算符是量子力学中的两个重要算符,它们描述了粒子的运动和旋转性质。
在量子力学中,一个物理量A的算符表示为^A,而物理量B的算符表示为^B。
首先,我们来定义角动量算符和动量算符:1. 角动量算符:在量子力学中,角动量算符通常用L表示,其三个分量的算符分别为^L_x,^L_y和^L_z。
2. 动量算符:动量算符通常用p表示,其三个分量的算符分别为^p_x,^p_y和^p_z。
然后,我们来讨论角动量算符平方和动量算符分量的对易关系。
在量子力学中,对易关系可以用来描述两个算符的关系,对易关系为[ ^A, ^B ] = ^A ^B - ^B ^A。
首先,我们来计算角动量算符平方和角动量分量的对易关系:( ^L_x )^2 = ^L_x ^L_x = ( ^L_x ^L_x - ^L_x ^L_x ) + ^L_x^L_x= ^L_x ( ^L_x ^L_x - ^L_x ^L_x ) + ^L_x ^L_x= [ ^L_x, ^L_x ] ^L_x + ^L_x ^L_x= 0 + ^L_x ^L_x= ^L_x ^L_x同理,可得( ^L_y )^2 = ^L_y ^L_y 和 ( ^L_z )^2 = ^L_z ^L_z。
接下来,我们来计算角动量平方与动量算符分量的对易关系:[ ( ^L_x )^2, ^p_x ] = ^L_x ^L_x ^p_x - ^p_x ^L_x ^L_x根据量子力学中的对易关系,角动量算符和动量算符的分量满足对易关系:[ ^L_i, ^p_j ] = iħ ε_ijk ^L_k其中ε_ijk是三维Levi-Civita符号,i,j,k可以取x,y,z。
带入上式:[ ( ^L_x )^2, ^p_x ] = ^L_x ^L_x ^p_x - ^p_x ^L_x ^L_x= ^L_x ħ ε_xyz ^L_z - ħ ε_xyz ^L_z ^L_x= ħ ε_xyz ( ^L_x ^L_z - ^L_z ^L_x )同理可得:[ ( ^L_y )^2, ^p_y ] = ħ ε_xyz ( ^L_y ^L_z - ^L_z ^L_y )[ ( ^L_z )^2, ^p_z ] = ħ ε_xyz ( ^L_z ^L_z - ^L_z ^L_z )可见,角动量算符平方和动量算符分量并不对易。




动量算符和角动量算符的对易关系
动量算符和角动量算符的对易关系是量子力学中一个重要的基本原理。
在物理学中,对易关系是指两个算符A和B,它们的对易子是0,即[A,B]=AB-BA=0。
如果两个算符A和B的对易子不等于0,那么它们是不对易的。
在量子力学中,动量算符和角动量算符的对易关系是:
[Px, Lz]=iħYx
[Py, Lz]=iħYy
[Pz, Lz]=iħYz
其中Px、Py和Pz分别表示沿着X、Y和Z方向的动量算符,Lz表示沿着Z方向的角动量算符,ħ是普朗克常数除以2π,而Yx、Yy和Yz 表示一个轨道角动量算符在X、Y和Z方向上的本征值,它们称为
“本征矢”。
这个对易关系告诉我们,在量子力学中,动量算符和角动量算符是互
相影响的。
如果我们测量一个粒子的动量,就会影响其角动量,并且
在测量其角动量时,会影响其动量。
这个关系是量子力学的基本原理
之一,它描述了物理世界的量子性质。
总的来说,动量算符和角动量算符的对易关系是量子力学中一个非常
重要的基本原理,它不仅仅涉及到动量和角动量的测量,还涉及到粒
子的本质结构和量子性质。
因此,对于每一个学习量子力学的人来说,理解动量算符和角动量算符的对易关系是非常必要的。
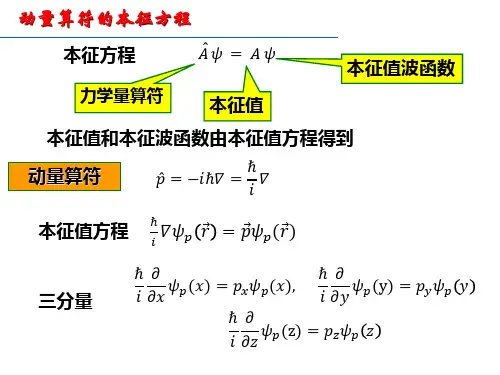


§3.2 动量算符和角动量算符一.动量算符。
1. 动量算符的本征值方程:()()r p r ip p ψψ=∇,三个分量方程是 (3.2.1) ()()r p r xi p x p ψψ=∂∂ , +∞<<∞-x ()()r p r yi p y p ψψ=∂∂ , +∞<<∞-y (3.2.2) ()()r p r zi p z p ψψ=∂∂ , +∞<<∞-z 通解是()r p i pCe r∙=ψ,C 是归一化常数。
(3.2.3) 2.动量本征函数的归一化。
()()()()()[]⎰⎰⎰⎰∞+∞-∞+∞-∞+∞-'-+'-+'-∙∞+∞-=dxdydze C d r r z p p y p p x p p ip pz z y y x x2τψψ因为()()x x x p p ip p dx ex x '-=⎰∞+∞-'-δπ2,所以有()()()()()()()()p p C p p p p p p C d r r z z y y x x p p'-='-'-'-=∙+∞∞-⎰δπδδδπτψψ323222如果取()232-= πC ,则()r pψ归一化为δ函数。
()()()()()r p i pp per p p d r r∙∙+∞∞-='-=⎰2321;πψδτψψ(3.2.4)(3.2.5)3.箱归一化在A (L/2,y,z )和A '(-L/2,y,z)点, ()r p i p Ce r∙=ψ的值应相同。
即⎪⎭⎫⎝⎛++⎪⎭⎫⎝⎛++-=z p y p L p i z p y p L p i z y x z y x CeCe2121()1=L p ix e所以πx xn L p 2=,x n 是正负整数或零。
,1,0,2±==x xx n Ln p π (3.2.6),1,0,2±==y yy n Ln p π (3.2.7),1,0,2±==z zz n Ln p π (3.2.8) 当L ∞→时,z y x p p p ,,的本征值就变为连续谱。

动量算符和角动量算符的交互作用动量算符和角动量算符的交互作用引言:动量和角动量是量子力学中非常重要的概念。
在量子力学中,我们通常使用算符来描述和操作物理量。
动量算符和角动量算符是两个关键的算符,它们在量子系统中起着至关重要的作用。
接下来,我们将深入探讨动量算符和角动量算符之间的交互作用,并分享我们对这个主题的观点和理解。
一、动量算符和角动量算符的定义和特性1. 动量算符:根据量子力学的原理,动量算符表示粒子的运动状态。
在一维情况下,动量算符可以表示为P = -iħ(d/dx),其中P是动量算符,ħ是约化普朗克常数,d/dx是对坐标的偏导数运算。
在三维情况下,动量算符变为P = -iħ(∇),其中∇是哈密顿算符。
2. 角动量算符:角动量算符描述了物体的自转和轨道运动。
在量子力学中,角动量算符一般用L来表示。
在三维情况下,角动量算符有三个分量:Lx、Ly和Lz,它们分别表示绕x、y和z轴的角动量。
3. 动量算符和角动量算符的特性:a. 动量算符和角动量算符都是厄米算符,即它们的本征值都是实数。
b. 动量算符和角动量算符之间满足对易关系:[P, Lx] = [P, Ly] = [P, Lz] = 0。
这意味着动量算符和角动量算符可以同时测量,不会相互干扰。
c. 角动量算符的三个分量之间也满足对易关系:[Lx, Ly] = iħLz,以及它们的循环置换关系。
二、动量算符和角动量算符的交互作用1. 薛定谔方程:在量子力学中,我们使用薛定谔方程来描述物体的量子态演化。
薛定谔方程中的哈密顿算符通常由动量算符和势能算符构成。
在一维情况下,薛定谔方程可以表示为HΨ = EΨ,其中H是哈密顿算符,Ψ是波函数,E是能量的本征值。
2. 动量和角动量的耦合:a. 动量和角动量之间的耦合通过角动量算符的导数来实现。
考虑一个单粒子系统,其哈密顿算符可以表示为H = (P^2/2m) + V(r),其中P是动量算符,m是质量,V(r)是势能。