第7章角动量资料
- 格式:ppt
- 大小:543.50 KB
- 文档页数:13



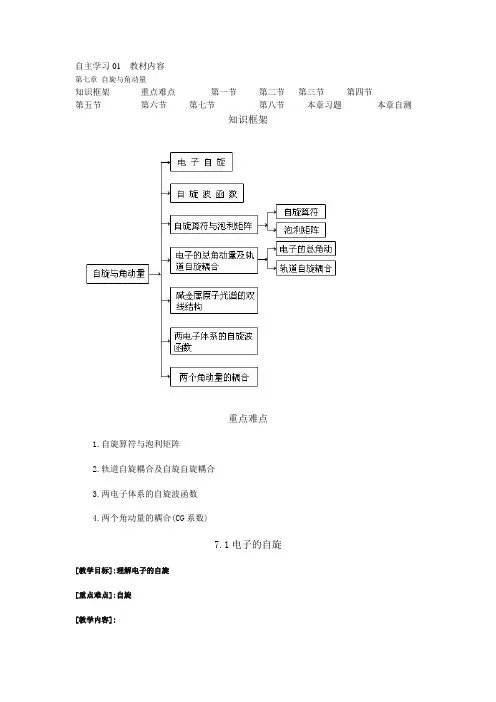
自主学习01 教材内容第七章自旋与角动量知识框架重点难点第一节第二节第三节第四节第五节第六节第七节第八节本章习题本章自测知识框架重点难点1.自旋算符与泡利矩阵2.轨道自旋耦合及自旋自旋耦合3.两电子体系的自旋波函数4.两个角动量的耦合(CG系数)7.1电子的自旋[教学目标]:理解电子的自旋[重点难点]:自旋[教学内容]:在较强的磁场下(∽T 10),我们发现一些类氢离子或碱金属原子有正常塞曼效应的现象,而轨道磁矩的存在,能很好的解释它但是,当这些原子或离子置入弱磁场(∽T 110-)的环境中,或光谱分辨率提高后,发现问题并不是那么简单,这就要求人们进一步探索。
大量实验事实证明,认为电子仅用三个自由度z ,y ,x 来描述并不是完全的。
我们将引入一个新的自由度—自旋,它是粒子固有的。
当然,自旋是Dirac 电子的相对论性理论的自然结果。
现在我们从实验事实来引入。
(1)电子自旋存在的实验事实(1)Stern-Gerlach 实验(1922年)当一狭窄的原子束通过非均匀磁场时,如果原子无磁矩,它将不偏转;而当原子具有磁矩μ,那在磁场中的附加能量为αμμcos B B U -=⋅-=如果经过的路径上,磁场在z 方向上有梯度,即不均匀,则受力dz dB U F αμcos =-∇=从经典观点看αcos 取值(从11--),因此,不同原子(磁矩取向不同)受力不同,而取值dz dB μ-—dz dB μ所以原子分裂成一个带。
但Stern-Gerlach 发现,当一束处于基态的银原子通 过这样的场时,仅发现分裂成二束,即仅二条轨道(两个态)。
而人们知道,银原子(47z =)基 态0l =,所以没有轨道磁矩,而分成二个状态(二 个轨道),表明存在磁矩,而这磁矩在任何方向上的 投影仅取二个值。
这磁矩既然不是由于轨道运动产生的,因此,只能是电子本身的(核磁矩可忽),这磁矩称为内禀磁矩sμ,与之相联系的角动量称为电子自旋,它是电子的一个新物理量,也是一个新的动力学变量。

角动量什么是角动量?在物理学中,角动量是描述物体旋转运动的一种物理量。
它与物体的惯性和旋转速度有关,用来描述物体围绕某个轴或中心进行旋转的能力或力矩。
角动量的定义角动量(L)的定义是物体的质量(m)与其线性速度(v)以及旋转半径(r)三个因素的乘积。
数学上可以表示为:L = mvr其中,L为角动量,m为物体的质量,v为物体的线速度,r为物体的旋转半径。
角动量的单位根据定义的公式可知,角动量的单位为千克·米²/秒(kg·m²/s)。
角动量的性质1.角动量是一个矢量量,具有大小和方向。
2.角动量是守恒量,即在没有外力矩作用下,系统的角动量保持不变。
3.当物体的质量或者速度增加时,角动量也会增加。
4.角动量的方向与线速度和旋转半径的方向相同。
角动量和力矩的关系角动量与力矩有着密切的关系。
根据角动量的定义,当物体受到力矩作用时,其角动量会发生变化。
根据牛顿第二定律和力矩的定义,我们可以得到以下公式:τ = ΔL/Δt其中,τ为力矩,ΔL为角动量的变化量,Δt为时间的变化量。
角动量守恒定律角动量守恒定律是一个重要的物理定律。
在一个孤立系统中,如果没有外力矩作用,系统的总角动量将保持不变。
这一定律的数学表达式为:L₁ + L₂ = L₃其中,L₁和L₂为系统中不同物体的角动量,L₃为系统的总角动量。
角动量在自然界中的应用角动量在自然界中的应用十分广泛。
以下是一些例子:1.行星绕太阳的运动:行星绕太阳的运动是一个典型的角动量守恒的例子。
根据开普勒定律,行星绕太阳的轨道面积速度是一个常数,即行星角动量守恒。
2.自行车或摩托车的稳定:自行车或摩托车在高速行驶时可以保持稳定,部分原因是由于车轮的角动量保持了平衡。
3.陀螺的稳定:陀螺通过旋转稳定自身的原理就是利用了角动量守恒。
结论角动量是描述物体旋转运动的重要物理量,它与物体的质量、线速度和旋转半径相关。
角动量具有一些重要的性质和守恒定律,对于理解自然界中旋转现象起到了重要的作用。

天宫课堂知识点总结角动量一、基本概念1. 角动量的定义角动量是一个物体运动状态的重要特征之一。
物体在运动过程中,除了具有动量外,还具有一种叫做角动量的运动状态特征。
角动量是描述物体自旋状态的物理量,它等于质点的质量与其到转轴的距离的乘积与质点运动速度的乘积,也可以用惯性矩阵产生。
通常用L 表示。
2. 角动量的定义公式角动量的定义公式为:L = r x p (矢量叉乘表示),其中L表示角动量,r表示质点到转轴的距离,p表示质点的动量。
3. 角动量的单位角动量的国际单位是牛·米(Nm),中文单位是牛·米(N·m)。
4. 角动量的矢量性角动量是一个矢量,具有大小、方向和作用线等特征,具有矢量性。
5. 角动量守恒定律若作用力矩与夹角之间平方反比关系(一般为-平方反比),则系统角动量守恒。
反之,若作用力矩与夹角成正比,系统的角动量守恒。
6. 角动量定理角动量定理是描述刚体上的力的运动学定理。
它宣称,如果一个刚体受到一个与它的CF 之间各元素连接直线垂直的力,那么刚体的角动量将以力矩的产生率的变化率增加。
7. 角速度、角位移和角加速度角速度是描述物体围绕旋转轴转动的快慢程度的物理量。
角位移是描述物体围着旋转轴旋转的一个角度大小的物理量。
角加速度是描述物体在单位时间内角速度改变量的物理量。
二、角动量定理1. 角动量定理的表述角动量定理是指:外力矩与时间的乘积等于物体的角动量的增量,即∑M = dL/dt。
2. 角动量定理的应用角动量定理可以应用于描述物体围绕一个固定轴旋转的角动量的变化规律。
在物理学中,角动量定理是用来描述刚体运动的一个基本定理。
三、角速度、坐标系和角加速度1. 角速度的定义和计算角速度是一个描述物体旋转快慢程度的物理量。
可以通过物体旋转的角度与旋转所花费的时间来计算。
2. 坐标系的选择在描述物体旋转的角速度和角动量时,需要选择合适的参照坐标系。
一般通过选择适当的坐标系,可以简化问题的分析。




角动量表达式角动量表达式角动量是物理学中一个非常基本的概念,它是描述物体旋转运动的特定量。
在量子力学中,角动量的概念更加广泛和深入,它对描述微观世界的物理过程和结果起着至关重要的作用。
本文将详细介绍角动量的概念和表达式。
一、角动量的概念角动量(Angular Momentum)是物理学中描述物体旋转运动的特定量。
简单来讲,旋转物体的角动量大小与物体质量、旋转速度以及旋转半径有关。
例如,一个以角速度ω绕某个轴旋转的质量为m的刚体,它的角动量公式可以表示为:L=Iω ——式(1)其中,I是该刚体绕轴的转动惯量,它是描述物体旋转惯性的物理量。
可以看出,物体的角动量随着其旋转的快慢以及转动惯量的大小而变化。
二、角动量的分类1.轨道角动量当物体绕某一中心轴旋转时,它产生的角动量称为轨道角动量(Orbital Angular Momentum)。
用符号L表示。
轨道角动量与物体质量、速度以及距离有关。
其表达式如下:L=r×p ——式(2)其中,r是物体相对于旋转轴的位置矢量,p是物体的动量矢量。
可以看出,物体的轨道角动量随着物体位置和动量的变化而变化。
2.自旋角动量自旋角动量(Spin Angular Momentum)是微观粒子的一个特殊性质,是除质量、电荷、磁矩外的一个基本属性。
用符号S表示。
自旋角动量是粒子自身的旋转运动,与粒子的质量和电荷无关。
其表达式如下:S=√s(s+1)h ——式(3)其中,s是自旋角动量大小,h是普朗克常数。
可以看出,自旋角动量大小取决于自旋量子数,而与物体位置和动量无关。
三、算符表示在量子力学中,物理量用算符表示。
角动量也不例外,它有一个对应的算符表示。
对于轨道角动量,它的算符表示为:L=xpy−yp x ——式(4)其中,x和y分别代表坐标方向,px表示动量x方向分量,py表示动量y方向分量。
对于自旋角动量,它的算符表示为:sz|s,m⟩=m|s,m⟩——式(5)其中,s和m分别代表自旋量子数和z方向自旋分量,|s,m⟩表示自旋态,sz是z方向自旋角动量算符。
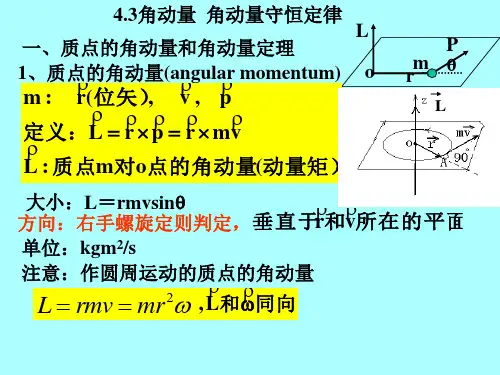
角动量守恒原理及讲解一、角动量的基本概念1. 定义- 对于一个质点,角动量→L=→r×→p,其中→r是质点相对于某参考点的位置矢量,→p = m→v是质点的动量(m为质点质量,→v为质点的速度)。
- 在直角坐标系中,如果→r=(x,y,z),→p=(p_x,p_y,p_z),那么L_x = yp_z - zp_y,L_y=zp_x - xp_z,L_z = xp_y - yp_x。
2. 单位- 在国际单位制中,角动量的单位是千克·米²/秒(kg· m^2/s)。
二、角动量定理1. 表达式- 对单个质点,→M=(d→L)/(dt),其中→M是作用在质点上的合外力矩。
- 对于质点系,→M_{外}=(d→L)/(dt),这里→M_{外}是系统所受的合外力矩,→L是系统的总角动量。
2. 物理意义- 角动量定理表明,作用于质点(系)的合外力矩等于质点(系)角动量对时间的变化率。
三、角动量守恒定律1. 内容- 当系统所受合外力矩→M_{外} = 0时,系统的角动量→L保持不变,即→L=text{常量}。
2. 条件- 合外力矩为零是角动量守恒的条件。
这可能有多种情况,例如:- 系统不受外力矩作用。
- 系统所受外力矩的矢量和为零。
在有心力场(如地球绕太阳的运动,太阳对地球的引力是有心力,力的作用线始终通过太阳中心)中,物体所受的力矩为零,角动量守恒。
3. 举例说明- 花样滑冰运动员的旋转- 当花样滑冰运动员双臂伸展时开始旋转,此时他具有一定的角动量。
由于冰面的摩擦力矩很小可以忽略不计,运动员所受合外力矩近似为零。
- 当他将双臂收拢时,他的转动惯量I减小(转动惯量I=∑ m_ir_i^2,双臂收拢时,身体各部分到转轴的距离r_i减小)。
根据角动量守恒定律L = Iω=text{常量}(ω为角速度),转动惯量I减小,则角速度ω增大,运动员的旋转速度加快。
- 行星绕太阳的运动- 行星受到太阳的引力是有心力,引力对太阳中心的力矩为零。
角动量知识点角动量是物体运动时重要的物理量,又称作运动量矩,是描述物体旋转的信息。
在物理学的高中阶段的学习中,角动量是一项基础而又重要的知识点。
本篇文章将深入介绍角动量的概念、计算方法以及角动量的应用。
概念角动量是物体在绕定轴旋转时所具有的物理量,因此角动量是一个向量。
具体来说,角动量 L 由旋转轴与旋转物体的线速度 v 以及物体的质量 m 组成。
其数学表达式为:L = mvr其中,r 表示物体到旋转轴的距离。
对于未旋转的物体而言,其角动量为零。
如果物体只是沿直线匀速运动,则其角动量也为零,因为这种情况下物体离旋转轴的距离为常数,且沿着同一方向运动。
只有物体绕着固定的轴旋转才有角动量。
计算方法为了计算物体的角动量,我们需要知道物体的线速度以及离旋转轴的距离。
在实际的问题中,物体的线速度通常是已知的,我们需要根据旋转情况来确定 r 的值。
对于一个固定的转轴而言,计算其绕轴旋转的物体的角动量时需要使用右手定则。
具体来说,我们可以将右手打成一个拳头,使得大拇指指向旋转轴的方向,当物体绕着该轴旋转时,四指的伸展方向表示物体绕轴旋转的旋转方向。
右手定则可以帮助我们确定旋转方向,进而计算角动量的方向。
应用角动量的物理意义在于它描述了物体的旋转。
在实际的问题中,角动量通常被用来描述物体的转动惯量、角加速度以及力矩等物理量。
例如,当物体受到外力作用时,角动量可以用来分析物体的旋转运动。
在空间中,很多天体都是通过旋转来保持稳定的状态。
例如,地球的自转、木星的自转以及各种星系的旋转等。
在这些天体中,角动量是一个重要的物理量,它可以帮助科学家们研究天体的性质以及未来的演化。
总结在物理学中,角动量是一个基础而又重要的物理量。
它描述了物体在绕定轴旋转时所具有的信息。
我们可以根据旋转轴以及旋转方向来计算物体的角动量,并将其应用于分析物体的旋转运动。
在空间天体的研究中,角动量也是一个重要的物理量。
我们需要掌握角动量的概念、计算方法以及应用场景,才能更好地理解物理学中的角动量知识点。