下载文档原格式
快速傅里叶变换FFT算法源码经典以下是一个经典的快速傅里叶变换（FFT）算法的源码，包含详细的注释解释每个步骤的作用。
```pythonimport cmath#递归实现快速傅里叶变换def fft(x):N = len(x)#基本情况：如果输入向量只有一个元素，则直接返回该向量if N <= 1:return x#递归步骤：#将输入向量分成两半even = fft(x[0::2]) # 偶数索引的元素odd = fft(x[1::2]) # 奇数索引的元素T = [cmath.exp(-2j * cmath.pi * k / N) * odd[k] for k in range(N // 2)]#组合结果return [even[k] + T[k] for k in range(N // 2)] + \[even[k] - T[k] for k in range(N // 2)]#逆傅里叶变换def ifft(X):N = len(X)#将输入向量取共轭X_conj = [x.conjugate( for x in X]#应用快速傅里叶变换x_conj = fft(X_conj)#将结果取共轭并归一化return [(x.conjugate( / N).real for x in x_conj]#示例测试if __name__ == "__main__":x=[1,2,3,4]X = fft(x)print("快速傅里叶变换结果：", X)print("逆傅里叶变换恢复原始向量：", ifft(X))```这个源码实现了一个经典的快速傅里叶变换（FFT）算法。
首先，`fft`函数实现了递归的快速傅里叶变换，接收一个输入向量`x`作为参数，返回傅里叶变换后的结果`X`。
如果输入向量只有一个元素，则直接返回。
否则，将输入向量分成两半，分别对偶数索引和奇数索引的元素递归应用FFT。
傅里叶变换公式傅里叶变换是数学中一种重要的变换方法，用于将一个函数从时域表示（函数在时间上的表示）转换为频域表示（函数在频率上的表示）。
它是由法国数学家约瑟夫·傅里叶于19世纪提出的，广泛应用于信号处理、图像处理、通信、音频处理等领域。
F(ω) = ∫f(t)e^(-jωt)dt其中，F(ω)表示频率为ω的正弦波在函数f(t)中的振幅，即将函数f(t)分解为振幅谱F(ω)。
e代表自然对数的底数，j表示虚数单位，ω为频率。
这个公式的意义在于将一个函数f(t)转换成一系列振幅谱F(ω)，表示不同频率正弦波在函数中所占的比重。
由于函数f(t)是由无数个不同频率的正弦波叠加而成的，因此通过傅里叶变换，我们可以分析一个函数中不同频率的成分。
这个过程也被称为频域分析。
傅里叶变换公式中的积分符号表示对整个时域进行积分，求出对应频率的振幅谱。
e^(-jωt)表示频率为ω的正弦波，振幅谱F(ω)表示频率为ω的正弦波在函数f(t)中的振幅。
通过在不同频率上进行积分，我们可以得到整个函数在频域上的表示。
傅里叶变换公式的应用非常广泛。
在信号处理领域，我们经常需要对信号进行频谱分析，以了解信号的频率成分。
例如，通过分析音频信号的频谱，我们可以分辨出不同乐器在音乐中的音高，从而实现音乐的识别和分类。
在图像处理领域，傅里叶变换可用于图像滤波、边缘检测等任务，提取图像中不同频率的特征。
此外，傅里叶变换还具有一些重要的性质，如线性性、位移性、尺度性等，这些性质使得傅里叶变换成为一种强大的工具。
例如，线性性质使得我们可以将傅里叶变换应用于信号的线性叠加，通过对不同频率的信号进行叠加，得到整体信号的频域表示。
总之，傅里叶变换是一种重要的数学工具，它能够将函数从时域表示转换为频域表示，帮助我们更好地理解信号和图像。
通过傅里叶变换，我们可以分析信号中不同频率的成分，实现信号处理、图像处理、通信等领域中的一系列任务。
光学经典理论｜傅里叶光学基础2018-02-24 17:00今天的光学经典理论为大家带来的是傅里叶光学基础，傅里叶光学是现代光学的一个分支，将电信理论中使用的傅里叶分析方法移植到光学领域而形成的新学科。
光学人们可以看看！在电信理论中，要研究线性网络怎样收集和传输电信号，一般采用线性理论和傅里叶频谱分析方法。
在光学领域里，光学系统是一个线性系统，也可采用线性理论和傅里叶变换理论，研究光怎样在光学系统中的传播。
两者的区别在于，电信理论处理的是电信号，是时间的一维函数，频率是时间频率，只涉及时间的一维函数的傅里叶变换；在光学领域，处理的是光信号，它是空间的三维函数，不同方向传播的光用空间频率来表征，需用空间的三维函数的傅里叶变换。
包含内容60年代发明了激光器，使人们获得了新的相干光源后，傅里叶光学无论在理论和应用领域均得到了迅速发展。
傅里叶光学运用傅里叶频谱分析方法和线性系统理论对广泛的光学现象作了新的诠释。
其主要内容包括标量衍射理论、透镜成像规律以及用频谱分析方法分析光学系统性质等。
推导演示一个光学信息系统和一个电学信息系统有许多相同之处，它们都是收集信息和传递信息，它们都有共同的数学工具──线性系统理论和傅里叶分析。
从信息论角度,关心的是信息在系统中传递过程;同样，对一个光学系统来讲，物和像的关系，也可以根据标量衍射理论由系统中光场的传播来确定，因此光学系统可以看成一个通信信道。
这样，通信理论中已经成熟的线性系统理论可以用来描述大部分光学系统。
当物体用非相干光照射时，在系统像平面上强度分布与物体上强度分布成线性（正比）关系。
而用来描述电学系统的脉冲响应h(t，τ)概念，即系统对一窄脉冲δ(t)（狄喇克δ函数）的响应，也可以用来描述光学系统，即用光学系统对点光源δ(x，y)的响应(点光源的像)h(x,y；ξ，η)来描述系统的性质，两者的区别仅仅在于电学系统的脉冲响应是时间一维函数，光学系统的脉冲函数是空间二维函数，另外两者都具有位移不变性，前者分布不随时间位移而变，后者分布不随空间位移而变（即等晕条件）。
常用傅里叶变换公式大全傅里叶变换是一种重要的数学工具，它可以将时域信号转换为频域信号，从而更好地理解信号的特性。
下面就是常用的傅里叶变换公式大全：1、傅里叶变换：$$F(u)=\int_{-\infty}^{\infty}f(x)e^{-2\pi iux}dx$$2、傅里叶反变换：$$f(x)=\int_{-\infty}^{\infty}F(u)e^{2\pi iux}du$$3、离散傅里叶变换：$$F(u)=\sum_{n=-\infty}^{\infty}f(n)e^{-2\pi iun}$$4、离散傅里叶反变换：$$f(n)=\frac{1}{N}\sum_{u=-\infty}^{\infty}F(u)e^{2\pi iun}$$5、快速傅里叶变换：$$F(u)=\sum_{n=0}^{N-1}f(n)W_N^{nu}$$6、快速傅里叶反变换：$$f(n)=\frac{1}{N}\sum_{u=0}^{N-1}F(u)W_N^{-nu}$$7、离散余弦变换：$$F(u)=\sum_{n=0}^{N-1}f(n)\cos\frac{(2n+1)u\pi}{2N}$$8、离散余弦反变换：$$f(n)=\frac{1}{N}\sum_{u=0}^{N-1}F(u)\cos\frac{(2n+1)u\pi}{2N}$$9、离散正弦变换：$$F(u)=\sum_{n=0}^{N-1}f(n)\sin\frac{(2n+1)u\pi}{2N}$$10、离散正弦反变换：$$f(n)=\frac{1}{N}\sum_{u=0}^{N-1}F(u)\sin\frac{(2n+1)u\pi}{2N}$$以上就是常用的傅里叶变换公式大全，它们可以帮助我们更好地理解信号的特性，并且可以用来解决许多实际问题。
因此，傅里叶变换在科学研究和工程应用中都有着重要的作用。
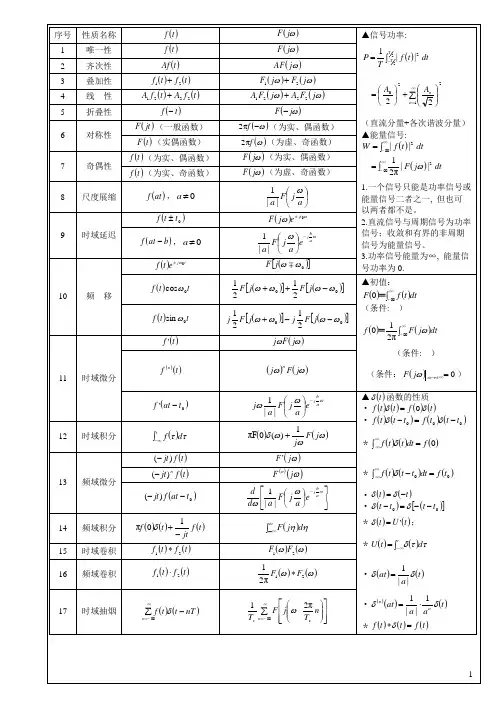
傅里叶变换的11个性质公式傅里叶变换的11个性质公式是傅立叶变换的基本性质，由他们可以推出其它性质。
其中包括线性性质、有穷性质、周期性质、旋转性质、折叠性质、应变性质、平移性质、对称性质、频域算子性质、滤波性质、压缩性质等共11条。
1、线性性质：如果x(t)和y(t)是两个信号，则有：X(ω)=F[x(t)]，Y(ω)=F[y(t)]，则有：X(ω)+Y(ω)=F[x(t)+y(t)]；αX(ω)=F[αx(t)]；X(ω)*Y(ω)=F[x(t)*y(t)]。
2、有穷性质：如果x(t)是有穷的，则X(ω)也是有穷的。
3、周期性质：如果x(t)在周期T内无穷重复，则X(ω)也在周期2π/T内无穷重复。
4、旋转性质：X(ω-ω0) = F[x(t)e^(-jω0t)]，即信号x(t)经过相位旋转成x(t)e^(-jω0t)，其傅里叶变换也会经过相位旋转成X(ω-ω0)。
5、折叠性质：X(ω+nω0)=F[x(t)e^(-jnω0t)]，即信号x(t)经过频率折叠后变为x(t)e^(-jnω0t)，其傅里叶变换也会经过频率折叠成X(ω+nω0)。
6、应变性质：X(aω)=F[x(at)]，即信号x(t)经过时间应变成x(at)，其傅里叶变换也会经过频率应变成X(aω)。
7、平移性质：X(ω-ω0) = F[x(t-t0)]，即信号x(t)经过时间平移成x(t-t0)，其傅里叶变换也会经过频率平移成X(ω-ω0)。
8、对称性质：X(-ω) = X*(-ω)，即傅里叶变换的实部和虚部对称。
9、频域算子性质：X(ω)Y(ω)=F[h(t)*x(t)]，即傅里叶变换不仅可以表示信号，还可以表示系统的频域表示，即h(t)*x(t)，其傅里叶变换为X(ω)Y(ω)。
10、滤波性质：H(ω)X(ω)=F[h(t)*x(t)]，即傅里叶变换可以用来表示滤波器的频域表示，即h(t)*x(t)，其傅里叶变换为H(ω)X(ω)。
傅里叶变换常用公式大全
傅里叶变换是一种将时域信号转换为频域信号的数学工具。
以下是傅里叶变换的常用公式：
1. 傅里叶变换公式：
F(ω) = ∫[−∞,+∞] f(t) e^(-jωt) dt
f(t) = ∫[−∞,+∞] F(ω) e^(jωt) dω
2. 傅里叶变换的线性性质：
F(a*f(t) + b*g(t)) = a*F(ω) + b*G(ω)
3. 傅里叶变换的频移性质：
F(f(t - τ)) = e^(-jωτ) F(ω)
4. 傅里叶变换的时移性质：
f(t - τ) = F^(-1)(ω) e^(jωτ)
5. 傅里叶变换的尺度变换性质：
F(f(a*t)) = (1/|a|) F(ω/a)
6. 傅里叶变换的对称性质：
F(-t) = F^*(ω)
f(-ω) = F^*(-t)
7. 傅里叶变换的卷积定理：
F(f * g) = F(f) * F(g)
8. 傅里叶变换的相关定理：
∫[−∞,+∞] f(t)g*(t) dt = 1/2π ∫[−∞,+∞]
F(ω)G^*(ω) dω
9. 傅里叶变换的能量守恒性质：
∫[−∞,+∞] |f(t)|^2 dt = 1/2π ∫[−∞,+∞]
|F(ω)|^2 dω
10. 傅里叶变换的Parseval定理：
∫[−∞,+∞] f(t)g*(t) dt = 1/2π ∫[−∞,+∞]
F(ω)G^*(ω) dω
以上是傅里叶变换的一些常用公式，可以用于分析和处理信号的频谱特性。
在实际应用中，根据具体问题选择合适的公式进行计算和推导。
