当前位置：文档之家 › 第3章 连续信号的频谱——傅里叶变换.

第3章 连续信号的频谱——傅里叶变换.

  • 格式：ppt
  • 大小：3.38 MB
  • 文档页数：197

下载文档原格式

  / 197

合集下载

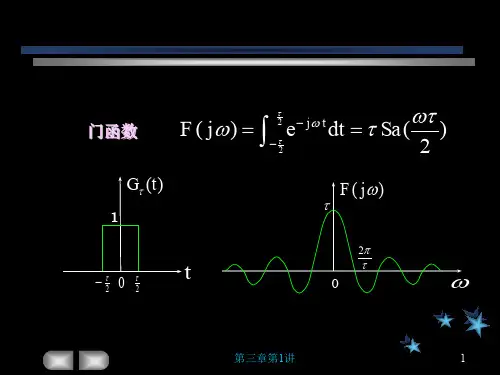
第三章傅里叶变换的性质.ppt

第三章傅里叶变换的性质.ppt


0
f (t)奇函数：X ()

f (t)sin tdt 2

f (t)sin tdt

0
X () 0
R() 0
可见，R()=R(- )为偶函数； X()= -X(- )为奇函数； 若 f (t)是实偶函数，F(j )=R() 必为实偶函数。 若 f (t)是实奇函数，F(j )=jX() 必为虚奇函数。

1 T

(t

T
)
F( j)
T
根据时域微分特性：
( j)2 F ( j) 1 e jT 2 1 e jT ,
0 2
T
TT
T

F(
j )

2
2T
(1
cosT )

4
2T
sin
2 (T
2
)

TSa2 (T
2
)
第三章第1讲

12
频域微分和积分特性
公式：
( jt)n f (t) F (n) ( j) f (0) (t) 1 f (t) F (1) ( j)
表明信号过延程时都了是t0在秒频并谱不搬会移改的变基其础频上谱完的成幅的度。，但是 使其相位变化了 - t0
频移特性： f (t)e j0 t F[ j( 0 )]
表明信号 f (t)乘以 e j0 t，等效于其频谱 F(j)沿频率右移 0
因为： cos 0 t

1 2
(e
j0 t

e
j0 t
)
sin
0t

1 2j
(e
j0 t

信号与系统第三章：傅里叶变换

信号与系统第三章：傅里叶变换

bn
n1
sin(n1t)
其中
an
,
bn
称为傅里叶系数，
1
2
T
。
16
傅里叶系数如何求得
Ci
t2 t1
f
(t
)
i
(t
)dt
t2
t1
i
2
(
t
)dt
1 Ki
t2 t1
f
(t
)
i
(t
)dt
式中： Ki
t2
t1
i
2
(t
)dt
an
2 T
T
2 T
f (t) cos(n1t)dt
2
a0 2
,
1 T
0 T
2
(1)
cos(n1t
)dt
2 T
T
2 0
cos(n1t
)dt
23
0
T
1
n1
2 T
sin(n1t
)
T 2
2 T
1
n1
sin(n1t
)
2 0
1
2
T
an
0
n 0,1, 2,3,L
24
bn
2 T
T
2 T
f (t) sin(n1t)dt
2
2 T
0 T
2
(1)
sin(n1t
)dt
2 T
T
2 0
26
T
T
0
T/ 2
t
0
T/ 2
t
(a)基波
(b)基波+三次谐波
0
T/ 2
Tt

信号与系统3.7.8傅里叶变换的基本性质

信号与系统3.7.8傅里叶变换的基本性质
2.若f(t)是虚函数 令f(t)＝jg(t)，则：
R()＝ g(t)sin (t)dt －
X ()＝ g(t) cos (t)dt －
在这种情况下，R()为奇函数，X()为偶函数，即满足： R()＝－R(－) X()＝X(－)
而 F() 仍是偶函数，()是奇函数。
第3章 傅里叶变换
此外，无论f(t)为实函数或复函数，都具有以下性质
所以
[F(t)]=2 f(－)
若f(t)是偶函数，式(3 50)变成
[F(t)]=2 f()
(3 50) (3 51)
第3章 傅里叶变换
第3章 傅里叶变换
（二） 线性（叠加性）
若 [fi (t)]＝Fi () （i＝1，2，...，n），则
n
n
[ aifi (t)]＝ aiFi ()
i＝1
f(at)e dt
令x=at
当a 0
[f(at)]＝ 1
f(x)e
j x a
dx=
1
F(
)
a
aa
第3章 傅里叶变换
当a 0
[f(at)]＝ 1
－
f(x)e
j
x a
dx
a ＋
＝－ 1
f(x)e
j
x
a dx＝－ 1
F(
)
a
aa
综合上述两种情况，便可得到尺度变换特性表达式为
[f(at)]＝ 1 F( )
－
－
在这种情况下，显然
R
X
()＝ －
()＝－
f(t) cos (t)dt
f(t) sin (t)dt
－
(3－54)
第3章 傅里叶变换

第三章连续信号的频谱介绍

第三章连续信号的频谱介绍

第三章连续信号的频谱介绍连续信号的频谱是指将连续信号在频域上的表示，它能够展示信号在不同频率上的能量分布情况。

频谱分析是信号处理中的重要内容，能够帮助我们理解信号的特性，并进行信号的分析与处理。

在本章中，我们将详细介绍连续信号的频谱分析方法和相关概念。

1.连续信号的频谱连续信号是指在时间上是连续变化的信号，可以通过连续时间的函数来表示。

在频域上，连续信号可以通过傅里叶变换来表示。

傅里叶变换将信号从时域转换到频域，给出了信号在不同频率上的能量分布情况。

连续信号的频谱是傅里叶变换结果的模值，它反映了信号在不同频率上的能量大小。

2.连续傅里叶变换连续傅里叶变换(CFT)是一种将连续信号从时域转换到频域的方法。

通过对连续信号进行积分运算，可以得到信号的频谱表示。

连续傅里叶变换的公式如下：F(ω) = ∫f(t)e^(-jωt)dt其中，F(ω)表示频率为ω的频谱，f(t)表示时域信号，e^(-jωt)是复指数函数。

通过计算不同频率ω下的复指数函数与信号的积分，可以得到连续信号的频谱。

3.连续信号的频谱性质连续信号的频谱具有以下几个重要性质：-零频率分量：频谱中的零频率分量表示了信号的直流分量，即信号在频域上的平均能量。

它在频谱中通常位于中心位置。

-频谱对称性：如果原始信号是实数信号，则频谱具有共轭对称性，即F(ω)=F*(-ω)，其中F*(-ω)表示F(ω)的共轭复数。

-线性性质：信号的线性组合的频谱等于各个信号频谱的线性组合。

-平移性质：将信号在时域上平移，会导致频谱在频域上平移同样的量。

- 抽样定理：如果信号的最高频率为f_max，则抽样频率f_s至少应为2f_max才能完整地恢复信号。

4.频谱分析方法为了获取连续信号的频谱信息，需要进行频谱分析。

-傅里叶变换：利用积分运算将信号从时域转换到频域。

-快速傅里叶变换(FFT)：快速傅里叶变换是一种高效的傅里叶变换算法，能够快速计算信号的频谱。

-功率谱密度(PSD)：功率谱密度是对信号能量在频域上进行定量描述的方法，可以用于分析信号的频率成分。

通信常见函数的傅里叶变换

通信常见函数的傅里叶变换

式中，n
arctan
bn an
cn
an2bn2
Opposite Hypotenuse
为n次谐波初始相位。 为n次谐波振幅。
！ 并非任意周期信号都能进行傅里叶级数展开！
f ( t ) 可展开为傅里叶级数的条件：
（1）f ( t 绝) 对可积，即： t2 f (t) dt t1
（2）f ( t 在) 区间内有有限个间断点；
第3章 傅里叶变换
重点：
1.傅里叶级数定义及适用条件 2.常见周期信号的频谱,非周期性信号的频谱 3.傅里叶变换的定义及适用条件及性质 4.周期信号的傅里叶变换 5.抽样定理 6.功率频谱与能量频谱 7.系统频域分析法 8.希尔伯特变换
3.1 傅里叶变换的产生
傅里叶1768年生于法国,1807年提 出“任何周期信号都可用正弦函数 级数表示”, 1822年在“热的分析 理论”一书中再次提出。1829年 狄里赫利给出傅里叶变换收敛条件。 傅里叶变换得到大规模的应用，则 是到了上世纪60年代之后。
T0 2
T0 2
(t)ejn0tdt1 T0
T0
(t)
1 T0
ejn0t
n
a0
1 T0
又
anT20 T2 T020(t)cosn0tdtT20
bn 0
T 0 ( t )
的三角傅里叶级数为：T0(t)T10 T20
cosn0t
n1
例 求下图中三角波的三角傅里叶级数。
解 （1）将周期函数 f ( t ) 在 t [0,T0]内的函数记为
第一个过零点为n =4 。 F&n 在2π/有4值1（谱线）
f (t)
1
T
2
o

信号与系统(郑君里第二版)讲义第三章 傅里叶变换

信号与系统(郑君里第二版)讲义第三章 傅里叶变换

t0
⎧0 ⎪T cos(mω1t )cos(nω1t )dt = ⎨ 1 ⎪2 ⎩T1
m≠n m=n≠0 m=n=0
∫
∫
t0 +T1
t0
0 ⎧ ⎪T sin (mω1t )sin (nω1t )dt = ⎨ 1 ⎪ ⎩2
m≠n m=n≠0
t0 +T1
t0
sin (mω1t )cos(nω1t )dt = 0 ，对于所有的 m 和 n
n =1
⎧ ⎪d 0 = a 0 ⎪ 2 2 ⎨d n = a n + bn ⎪ an ⎪θ n = arctan bn ⎩
n = 1,2,3,L n = 1,2,3,L
三、虚指数形式的傅里叶级数 任何周期信号 f (t ) 可以分解为
f (t ) =
n =−∞
∑ Fe
n
∞
jnω1t
傅里叶系数：
Fn = 1 t0 +T1 f ( t ) e − jnω1t dt ∫ t 0 T1
f (t )
E 2
−
T1 2
0
T1 2
t
奇函数的傅里叶级数展开式的系数为： a0 = an = 0
4 bn = T1
Fn = −
∫ f (t )sin (nω t )dt
1
T1 2 0
1 π jbn ， ϕ n = − 2 2
6
奇函数的 Fn 为虚数。在奇函数的傅里叶级数中不会含有余弦项，只可能含 有正弦项。 3、奇谐函数（半波对称函数） 若波形沿时间轴平移半个周期并相对于该轴上下反转， 此时波形并不发生变 化，即满足 ⎛ T ⎞ f (t ) = − f ⎜ t ± 1 ⎟ 2⎠ ⎝ 这样的函数称为半波对称函数或称为奇谐函数。 奇谐函数的傅里叶级数展开式的系数为： a0 = 0 an = bn = 0 （ n 为偶数） （ n 为奇数）

第3章 连续信号的频谱傅里叶变换

第3章 连续信号的频谱傅里叶变换
• 傅里叶分析方法不仅应用于电力工程、通信和控制领域之中， 而且在力学、光学、量子物理和各种线性系统分析等许多有关 数学、物理和工程技术领域中得到广泛的应用。
• 本章讨论的路线：
• 傅里叶级数正交函数——傅里叶变换，建立信号频谱的概念；
• 通过典型信号频谱以及傅里叶变换性质的研究，掌握傅里叶分 析方法的应用。
第3章 连续信号的频谱 傅里叶变换
2020年4月22日星期三
本章的主要内容：
1、周期信号的傅里叶级数分析 2、典型周期信号的傅里叶级数 3、傅里叶变换 4、典型非周期信号的傅里叶变换 5、冲激函数和阶跃函数的傅里叶变换 6、傅里叶变换的基本性质 7、卷积特性（卷积定理） 8、周期信号的傅里叶变换 9、抽样信号的傅里叶变换 10、抽样定理
例子
以下为对称方波，注意不同的项数，有限级数对 原函数的逼近情况，并计算由此引起的方均误差 解：其傅。里叶级数表达式为 ：
只取基 波分量 一项
取基波分量和 三次谐波分量
取基波、三次谐 波分量和五次谐 波分量
从上面例子看出：
（1）n愈大，则愈逼近原信号f(t)。
(2) 当信号f(t)是脉冲信号时，其高频分量主要影响脉冲的跳变沿； 低频分量影响脉冲的顶部。f(t)波形变化愈剧烈，所含的高频分量 愈丰富；f(t)变化愈缓慢，所含的低频分量愈丰富。
作业
P160 3-1，3-2，3-3，3-8
第三节 典型周期信号的
傅里叶级数
典型周期信号的傅里叶级数
•典型周期信号的频谱分析可利用： 傅里叶级数 或傅里叶变换 •介绍的典型周期信号有如下： 1、周期矩形脉冲信号 2、周期锯齿脉冲信号 3、周期三角脉冲信号 4、周期半波余弦信号 5、周期全波余弦信号
1、周期矩形脉冲信号 (1)周期矩形脉冲信号的傅里叶级数求解

第3章 连续信号的频谱——傅里叶变换

第3章 连续信号的频谱——傅里叶变换

• 直到19世纪末，制造出电容器。20世纪初，谐振电路、滤波
器、正弦振荡器等一系列问题的解决为正弦函数与傅里叶分 析的在通信系统中的应用开辟了广阔的前景。 • 从此，在通信与控制系统的理论研究和实际应用之中，采用 频率域（频域）的分析方法比经典的时间域（时域）方法有 许多突出的优点。 • 当今，傅里叶分析方法已成为信号分析与系统设计不可缺少 的重要工具。 • 20世纪70年代，出现的各种二值正交函数（沃尔什函数）， 它对通信、数字信号处理等技术领域的研究提供了多种途径 和手段。使人们认识到傅里叶分析不是信息科学与技术领域 中唯一的变换域方法。
nw1 nw1

0
w
nw1
w1 0 w1
nw1
w
正、负频率相应项成对合并，才是实际频谱函数。
4.周期信号的功率特性
—时域和频域能量守恒定理
周期信号的平均功率P：在一个周期内求平方再求积分。
1 t0 T1 2 f (t )dt P f (t ) t T1 0 1 1 2 2 2 2 2 a0 ( an bn ) c0 cn 2 n 1 2 n 1
其傅里叶级数三角展开式中 仅含基波和奇次谐波
例子
例如：奇谐函数
f (t )
E 2
T1 2
f (t )
E 2
T 1 2
0
E 2
T1 2
t
0
E 2
T1 2
t
sin( w1t )
E 2
f (t )
E 2
T1 2 T 1 2 T1 2
f (t )
0
E 2
t

0
E 2
T1 2

033第三章 傅里叶变换

033第三章 傅里叶变换

T 0
f
2(t)d t
a02
1 2 n1
an2
bn2
a02
1 2
cn2
n1
Fn
n
2
这是帕塞瓦尔定理在傅里叶级数情况下的具体体现; 表明：
周期信号平均功率=直流、基波及各次谐波分量 有效值的平方和；
也就是说，时域和频域的能量是守恒的。 Fn 2 ~ 绘成的线状图形，表示 各次谐波的平均功率 随频率分布的情况，称为功率谱系数。
第三章 傅里叶变换
3.1 引言
X
频域分析
第 2
页
频域分析将时间变量变换成频率变量，揭示了信 号内在的频率特性以及信号时间特性与其频率特性之 间的密切关系，从而导出了信号的频谱、带宽以及滤 波、调制和频分复用等重要概念。
从本章开始由时域转入变换域分析，首先讨论傅里 叶变换。傅里叶变换是在傅里叶级数正交函数展开的基 础上发展而产生的，这方面的问题也称为傅里叶分析 （频域分析）。将信号进行正交分解，即分解为三角函 数或复指数函数的组合。
第第 2222
页页
偶函数 奇函数 奇谐函数 偶谐函数
注：指交流分量
X
第第
1．偶函数
2233
页页
信号波形相对于纵轴是对称的
f (t) f (t)
f (t) E
bn 0
4
an T
T
2 0
f (t)cosn1t d t
0
F
n
F (n1 )
1 2
an
jbn
1 2
an
T
O
n 0
T
t
傅里叶级数中不含正弦项，只含直流项和余弦项。
n
Fn1

――傅里叶变换

――傅里叶变换

第三章傅里叶变换（一）三角函数形式的傅里叶级数满足狄利赫里条件的周期函数f。

）可由三角函数的线性组合来表示，若f（t）的周期为T，角频率3 =之，频率f ='，傅里叶级数展开表达式 1 1 T 1 T1 1为f (t)= a +£[a cos(〃3t)+ b sin (〃3t)n=1各谐波成分的幅度值按下式计算a = —f t o+T1 f (t)dto T t o a =」t o+T1 f (t)cos (n3 t)dt n T t1ob = — j t o+ T1 f (t)sin(n3 t)dt n T t1o其中n = 1,2, •••狄利赫里条件:（1）在一个周期内，如果有间断点存在，则间断点的数目应是有限个;（2）在一个周期内，极大值和极小值的数目应是有限个；（3）在一个周期内，信号是绝对可积的，即』t o+T|f （t）dtt等于有限值。

t o（二）指数形式的傅里叶级数周期信号的傅里叶级数展开也可以表示为指数形式，即f (t)= £F (n3)ej n31 n1n二一8其中F = — f t o+T1f 0-加3 t dt n T1 t o 其中n为从一8到+8的整数。

3.1m号的傅里叶级!瞬析(三)函数的对称性与傅里叶系数的关系(1)偶函数由于f。

)为偶函数，所以f(t)sin(旭t)为奇函数，则1b = — J t o+ T i f (t)sin (n① t)dt = 0 n T t11 0所以，在偶函数的傅里叶级数中不会含有正弦项，只可能含有直流项和余弦项。

(2) 奇函数由于f (t)为奇函数，所以f(t)cos (n o t )为奇函数，则1a =— J t0+T f (tb t = 00 T t10a = — J t0+T1 f (t)cos (n0 t)dt = 0 n T t11t0所以，在奇函数的傅里叶级数中不会含有直流项和余弦项，只可能包含正弦项(3)奇谐函数(f (t )=-f [ t + T ])I 27半波对称周期函数的傅里叶级数中，只会含有基波和奇次谐波的正、余弦项，而不会含有偶次谐波项，这也是奇谐函数名称的由来。

信号课件第三章傅里叶变换

信号课件第三章傅里叶变换
• 从本章起，我们由时域分析进入频域分析，在频域分析中， 首先讨论周期信号的傅里叶级数，然后讨论非周期信号的 傅里叶变换。傅里叶变换是在傅里叶级数的基础上发展而 产生的，这方面的问题统称为傅里叶分析。
• 任何周期函数在满足狄义赫利的条件下，可以展成正交函 数线性组合的无穷级数。如果正交函数集是三角函数集或 指数函数集，此时周期函数所展成的级数就是“傅里叶级 数”。
T1 T1 T1 2
f (t) sin n1tdt 0
2 T1
a0 T1
2
an T1
2 T1
T21
2 T1
2
f (t)dt
f (t) c
2f T1 0
osn1tdt
(t)dt
4 T1
T1 2
0
f (t) cosn1tdt
所以，在偶函数的傅里叶级数中不会有正弦项，只可能 含有（直流）和余弦分量。
α>0
F (w) f (t)e jwt dt ete jwt dt 1
0
jw
f (t) 1
t
F(w) 1
2 w2
1/ F( j)
(
)
arctan(
)
( )
/2
/2
2、双边指数信号
f (t)
f (t) e t α>0
1
2/ F()
F (w) f (t)e jwt dt
dt
E
e jnw1t
/2
E
e jnw1 / 2 e jnw1 / 2
T / 2
T
jnw1
T
/ 2
jnw1
Ts
t
2E T
e jnw1 / 2 e jnw1 / 2 2 jnw1

第三章 傅里叶变换

第三章 傅里叶变换

P=a
2 0
1 2
n 1
an2 bn2
c02
1 2
cn2
n 1
n
Fn
2
；
3、一个特别的性质： e jn e jn
3.1.3 函数的对称性与傅里叶系数的关系
1、波形对称分类：（1）、整周期对称，例如偶函数和奇函数，其可决定级数中只可能含有余弦项或正弦项；（2）半 周期对称，例如奇谐函数，其可决定级数中只可能含有偶次项或奇次项。 2、对称条件： （1）、偶函数：若信号波形相对于纵轴是对称的，即满足 f(t)=f(-t),此时 f(t)是偶函数，偶函数的 Fn 为实数。在偶函 数的傅里叶级数中不会含有正弦项，只可能含有直流项和余弦项。 （2）奇函数：若波形相对于纵坐标是反对称的，即满足 f(t)=-f(-t),此时 f(t)是奇函数，奇函数的 Fn 为虚数。在奇函数 的傅里叶级数中不会含有余弦项，只可能含有正弦项。虽然在奇函数上加以直流成分，它不再是奇函数，但在它的 级数中仍然不会含有余弦项。 （3）寄谐函数：若波形沿时间轴平移半个周期并相对于该轴上下翻转，此时波形并不发生变化，即满足：
n2 1 2
) cos n1t
基波和偶次谐波频率分量。谐波幅度以 1 规律收敛。 n2
其中1
=
2 T1
；其频谱只包含直流、
3.2.5 周期全波余弦信号
1、周期全波余弦信号的傅里叶级数为：
f
(t)
2E
4E 3
cos(1t)
4E 15
cos(21t)
4E 35
cos(31t)
2E
4E
1n 1
第三章 傅里叶变换
傅里叶变换是在傅里叶级数正交函数展开的基础上发展而产生的；

信号与系统第3章 傅里叶变换

信号与系统第3章 傅里叶变换

P
f
2 (t) 1 T1
t0 T1 t0
f
2 (t)d t
a0 2
1 2
n1
(an
2
bn 2 )
2
Fn _____ 帕塞瓦尔定理
n
结论：周期信号的平均功率等于傅里叶级数展开 式中基波分量及各谐波分量有效值的平方 和，即时域和频域的能量守恒。
五. 周期信f号(t)的频c0 谱 （c三n c角os函(n数1t形 式n )） n1
(1) 偶函数 f (t) f (t)
4
an T1
T1
2 0
f (t) cos(n1t)dt
Fn
Fn
an 2
bn 0
傅里叶级数中不会含有正弦项， 只可能含有直流项和余弦项。
(2) 奇函数 f (t) f (t)
a0 0 , an 0
bn
4 T1
T1
2 0
f (t) sin(n1t)d t
e j n1t
T1 n 2
画频谱图：
c0
a0
E
T1
an
2E
T1
Sa
n1
2
, n
1,2,
cn an
1）令 m
2
得
2
m
即在
2
m，m为整数处有零点。
2）
2
2
T1
T1
零点间谱线个数
3) c n值为正，相位为0，值为负，相位为π
4)谱线间隔为 1 带宽
2
T1
，第一个过零点带宽定义为信号的
1 3
s in31t
1 4
sin41t
E
1 n1

信号分析与处理-傅里叶变换

信号分析与处理-傅里叶变换

第三章傅里叶变换本章提要：◆傅里叶级数（Fourier Series）◆非周期信号的傅里叶变换◆傅里叶变换的性质◆周期信号的傅里叶变换◆采样信号和采样定理J.B.J. 傅里叶（Fourier）◆1768年生于法国◆1807年提出“任何周期信号都可用正弦函数级数表示”，但其数学证明不很完善。

◆拉普拉斯赞成，但拉格朗日反对发表◆1822年首次发表在《热的分析理论》◆1829年狄里赫利第一个给出收敛条件周期信号都可表示为谐波关系的正弦信号的加权和非周期信号都可用正弦信号的加权积分表示傅里叶分析方法的应用：（1）泊松（Possion）、高斯（Gauss）等将其应用于电学中；（2）在电力系统中，三角函数、指数函数及傅里叶分析等数学工具得到广泛的应用。

（3）20世纪以后，在通信与控制系统的理论研究与实际应用中开辟了广阔的前景。

（4）力学、光学、量子物理和各种线性系统分析等得到广泛而普遍的应用。

§ 3.1 周期信号的傅立叶级数◆三角函数形式的傅里叶级数◆复指数形式的傅里叶级数◆几种典型周期信号的频谱◆吉伯斯现象一、三角函数形式的傅里叶级数∞Tianjin University Tianjin University二、复指数形式的傅里叶级数周期信号的复数频谱图三、几种典型周期信号的频谱+-1T t tjn ωTianjin UniversityTianjin University∞n A τωτ思考题：KHz T f T 100101011 26=⨯===-，πω2. 奇函数：f (t )= -f (-t)1tω只含正弦项n F =3.奇谐函数T四、吉伯斯现象)(t f有限项的N越大，误差越小例如: N=11§ 3.2 非周期信号的傅立叶变换∞从物理意义来讨论傅立叶变换(FT)Tianjin University Tianjin UniversityTianjin UniversityTianjin University )0>arctg -=)(t f时域中信号变化愈尖锐，其频域所包含的高频分量就愈丰富；反之，信号在时域中变化愈缓慢，其频域所包含的低频分量就愈多。

信号与系统3章_傅里叶变换

信号与系统3章_傅里叶变换

2A t A sin n0t f AC (t ) cos n0 d T0 n1 π n1 n
fD A / 2
故
A A sin n0t f (t ) 2 π n 1 n
（2）利用直接法求解
1 a0 T0

0 T0

A A tdt T0 2
（2）双边频谱：
1 Fn T
1 e jn1 t / 2 e dt T jn1
/2
jn1 t / 2 / 2
2 sin 21 b b 2 4ac T n1 2a
n
1 n1 sin n 2 n1 Sa( ), T T 2 2
偶谐函数
2．横轴对称性
（1）奇谐函数的傅里叶级数中只有奇次谐波分量。 （2）偶谐函数的傅里叶级数中只有偶次谐波分量。
如果原信号既不是奇谐函数也不是偶谐函数，
那么其傅里叶级数展开式中就会既包含有奇次谐 波分量也包含有偶次谐波分量。
！ 利用奇谐函数、偶谐函数性质的时候，最好将
其直流分量去掉，以免发生误判。
an 0
2 bn T0
故
A A T0 T0 t sin n0tdt nπ
0
A A sin n0t f (t ) 2 π n 1 n
3.2.3 傅里叶级数的MATLAB仿真实现
常称为f(t)的截断傅里叶级数表示式。
f (t )
n N
Fe
n
N
jn1t
t
f (t ) E
2
f (t )
E 2 T1 2

T1 2
o
sin 21 t
E 2

傅里叶变换详细讲述

傅里叶变换详细讲述

第三章傅里叶变换3-1 概述对于一件复杂的事情，人们总是从简单的一步开始做起，富丽堂皇的高楼大厦，是人们一块砖一块砖垒起来的。

为了简化问题的求解，人们往往也使用“变换分析”这种技巧，所起“变换”大家可能会感到陌生，其实我们在中学时已经运用了“变换分析”技巧，大家一定还记得对数运算，它实际上也是一种数学变换，我们知道两个数的乘积的对数等于两个数的对数和，两个数的商的对数等于这两个数的对数差，利用对数这个运算规则我们可以将数的乘积运算转换（准确地说变换）为数的加法运算，可以将数的除法运算转换（变换）为数的减法运算，可见“变换分析”给我们解决问题带来了方便，傅里叶变换就是给我们分析问题和解决问题极为方便的数学工具。

线性非时变系统的卷积分析实际上是基于将输入信号分解为一组加权延时的单位冲激（或样值）激励的线性组合。

本章将讨论信号和系统的另一种表示，其基本观点还是将信号分解为一组简单函数的线性组合，但是这里用的简单函数不是单位冲激（或样值）而是三角函数（或复指数函数）。

用“三角函数和”表示信号的想法至少可以追溯到古代巴比伦时代，当时他们利用这一想法来预测天体运动。

这一问题的近代研究始于1748年，欧拉在振动弦的研究中发现：如果在某一时刻振动弦的形状是标准振动（谐波）模的线性组合，那么在其后任何时刻，振动弦的形状也是这些振动模的线性组合。

另外，欧拉还证明了在该线性组合中，其后的加权系数可以直接从前面时间的加权系数中导出。

欧拉的研究成果表明了：如果一个线性非时变系统输入可以表示为周期复指数或正弦信号的线性组合，则输出也一定能表示成这种形式。

现在大家已经认识到，很多有用的信号都能用复指数函数的线性组合来表示，但是在18世纪中期，这一观点还进行着激烈的争论。

1753年D.伯努利（D.Bernoulli）曾声称：一根弦的实际运动都可以用标准（谐波）振荡模的线性组合来表示。

而以J.L.拉格朗日(grange)为代表的学者强烈反对使用三角级数来研究振动弦运动的主张，他反对的论据就是基于他自己的信念，即不可能用三角级数来表示一个具有间断点的函数。

第三章 傅里叶变换

第三章 傅里叶变换

τ τ
2 2
其傅里叶变换为 ：
F (Ω ) =
∫
∞
2E Ωτ = ∫ τ Ee dt = sin( ) −2 Ω 2 Ωτ sin( ) 2 = E τ Sa Ω τ = Eτ Ωτ 2 2
τ
2
−∞
f ( t ) e − j Ω t dt
− jΩ t
可以看出傅里叶变换与傅里叶系数有如下关系： 可以看出傅里叶变换与傅里叶系数有如下关系：
傅里叶的两个最主要的贡献—— 傅里叶的两个最主要的贡献 “周期信号都可以表示为成谐波关 系的正弦信号的加权和” 系的正弦信号的加权和”——傅里 傅里 叶的第一个主要论点 “非周期信号都可以用正弦信号的 加权积分来表示” 加权积分来表示”——傅里叶的第 傅里叶的第 二个主要论点
§3 傅里叶变换
3.2信号的傅里叶变换 信号的傅里叶变换
E f (t) = 0 | t |<
f(t) E
τ
2 T 2
-T -τ
2
τ
< | t |<
0
τ
2
T
t
τ：脉冲宽度， E：幅度， T：重复周期。 ：脉冲宽度， ：幅度， ： 这个周期性脉冲函数可以展开成傅里叶级数： 这个周期性脉冲函数可以展开成傅里叶级数：
f (t ) =
n = −∞
π ϕ (Ω ) = 2 π − 2 Ω < 0 Ω > 0
-
-α
0
α
Ω
ϕ(Ω) π
2
π
2
Ω
４ 单位冲激函数
其傅里叶变换为： 其傅里叶变换为： ∞ F (Ω ) = ∫ δ (t )e − ∞ 根据冲激函数的定义， 根据冲激函数的定义，有
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
n 1

其中基波——角频率为1的分量; n次谐波——角频率为n1的分量
1 t0 T1 1 T1 直流分量：a0 t0 f (t )dt 0 f (t )dt T1 T1 2 t0 T1 其中 余弦分量幅度：an f (t ) cos(n1t )dt t0 T 1 2 t0 T1 f (t ) sin(n1t )dt 正弦分量幅度：bn t T1 0 n 1, 2, ...

0
w1 3w1
nw1
w
二、指数形式的傅里叶级数
1、指数形式的傅里叶级数的形式
2 设f(t) 为任意周期信号（周期 T1 , 角频率1 ） T1
则其可展开为指数形式的傅里叶e
1

jn1t
2.指数形式的傅里叶级数中各个量之间的关系
1 t0 T1 jn1t 记 Fn f (t )e dt 复函数：F (n1 ) t0 T 1 其中 n ~ 直流分量：F0 c0 a0
一周期内仅有限个间断点； 一周期内仅有限个极值； t0 T1 f (t ) dt 一周期内绝对可积， t 0
通常所遇到的周期性信号都能满足此条件，因此， 以后除非特殊需要，一般不再考虑这一条件。
4、基波、谐波
2 通常把频率为： f1 T1 称为基波。 w1 2 频率为：2 f1 2T1 2 称为二次谐波。 w1 2 称为三次谐波。 频率为： 3 f1 3T1 3 w1
• 直到19世纪末，制造出电容器。20世纪初，谐振电路、滤波
器、正弦振荡器等一系列问题的解决为正弦函数与傅里叶分 析的在通信系统中的应用开辟了广阔的前景。 • 从此，在通信与控制系统的理论研究和实际应用之中，采用 频率域（频域）的分析方法比经典的时间域（时域）方法有 许多突出的优点。 • 当今，傅里叶分析方法已成为信号分析与系统设计不可缺少 的重要工具。 • 20世纪70年代，出现的各种二值正交函数（沃尔什函数）， 它对通信、数字信号处理等技术领域的研究提供了多种途径 和手段。使人们认识到傅里叶分析不是信息科学与技术领域 中唯一的变换域方法。
第二节 周期信号的傅里 叶级数分析
一、三角函数形式的傅里叶级数 1、一种三角函数形式的傅里叶级数
2 设f(t) 为任意周期信号（周期 T1 , 角频率1 ） T1
则其可展开为三角函数形式的傅里叶级数
f (t ) a0 an cos(n1t ) bn sin(n1t )
第三章
连续信号的频谱——傅里叶变换
本章的主要内容：
1、周期信号的傅里叶级数分析 2、典型周期信号的傅里叶级数 3、傅里叶变换 4、典型非周期信号的傅里叶变换 5、冲激函数和阶跃函数的傅里叶变换 6、傅里叶变换的基本性质 7、卷积特性（卷积定理） 8、周期信号的傅里叶变换 9、抽样信号的傅里叶变换 10、抽样定理
第一节 引言
傅里叶分析发展史
• 从本章开始由时域分析转入频域分析。 • 傅里叶变换是在傅里叶级数正交函数展开的基础上发展而产 • •
• •
生的。 傅里叶分析的研究与应用经历了一百余年。 1822 年法国数学家傅里叶（ J.Fourier,1768-1830 ）在研究 热传导理论时发表了“热的分析理论”著作，提出并证明了 将周期函数展开为正弦级数的原理，奠定了傅里叶级数的理 论基础。 泊松（Poisson）、高斯（Gauss）等人把这一成果应用到电 学中去。 伴随电机制造、交流电的产生与传输等实际问题的需要，三 角函数、指数函数以及傅里叶分析等数学工具已得到广泛的 应用。
可见，直流分量的大小以及基波与各次谐波的 幅度、相位取决于周期信号的波形。
5、幅度谱、相位谱
单边频谱图：cn ~ n1 信号的幅度谱
cn c0
c1
n ~ n1 信号的相位谱
c2
c3
其中各频率分量幅度称为“谱线”； 连各谱线顶点的曲线称为
nw1
0
w1
n
3w1
w
? 包络线”。
周期信号的主要特点： 具有离散性、谐波性、收敛性
• 但傅里叶分析始终有着极其广泛的应用，它是研究其他变换方
•
•
• • • •
法的基础。而且出现了”快速傅里叶变换（FFT）”它给傅里 叶分析这一数学工具增添了新的生命力。 傅里叶分析方法不仅应用于电力工程、通信和控制领域之中， 而且在力学、光学、量子物理和各种线性系统分析等许多有关 数学、物理和工程技术领域中得到广泛的应用。 本章讨论的路线： 傅里叶级数正交函数——傅里叶变换，建立信号频谱的概念； 通过典型信号频谱以及傅里叶变换性质的研究，掌握傅里叶分 析方法的应用。 对于周期信号而言，进行频谱分析可用傅里叶级数或傅里叶变 换；傅里叶级数相当于傅里叶变换的一种特殊表达形式。 最后对研究周期信号与抽样信号的傅里叶变换，并介绍抽样定 理，抽样定理奠定了数字通信的理论基础。
当n 0时，Fn Fn 1 1 j n a jb F F e (an jbn ) e 2 n n n n 2 1 2 1 2 其中 Fn a n bn cn 2 2 n n (三角函数形式）
T1 T1 为了积分方便，通常取积分区间为： 0 ~ T1或 ~ 2 2
三角函数集是一组完备函数集。
2、另一种三角函数形式的傅里叶级数
f(t) 展开为常用形式
f (t ) c0 cn cos(n1t n ) 或
n 1
f (t ) d 0 d n sin(n1t n )
n 1
c0 d 0 a0 2 2 其中 cn d n a n bn bn an arctg , arctg n n a bn n
3、傅里叶级数展开的充分条件
傅里叶级数存在的充分条件： 周期信号f(t)须满足“狄利克雷”(Dirichlet)条件，即