第matlab计量经济学多重共线性的诊断与处理
- 格式:doc
- 大小:154.00 KB
- 文档页数:15

多重共线性的诊断方法和解决方法综述-计量经济学论文-经济学论文——文章均为WORD文档,下载后可直接编辑使用亦可打印——摘要:多元线性回归模型的经典假定之一是解释变量之间不存在线性关系。
但在实际应用中,多元线性回归模型中的解释变量之间往往存在近似的线性关系,如果仍然用最小二乘法估计模型,会造成分析结果不准确甚至严重偏离变量间本来的依存关系。
为此,首先总结了多重共线性的检验方法,然后探讨了多重共线性常用的修正方法,最后结合实例演绎了逐步回归法和主成分回归法的具体应用,为现实经济问题中多重共线性的检验与处理提供一定借鉴。
关键词:多重共线性; 诊断; 补救措施; 逐步回归法; 主成分回归;Abstract:There being no linear relationship among interpretation variables is one of the classical assumptions in multiple linear regression model.However,in the practical application,there is often an approximate linear relation.If we still use the method ofordinary least squares to estimate the model,the result may become incorrect and even far from the original relationship among the variables.Therefore,the paper first summarizes the test methods of Multicollinearity.And then,the paper summarizes the commom correction methods of multicollinearity.Finally,the application of stepwise regression and principal component regression is deduced by using an example.The research will provide some reference for the test and treatment of multicollinearity in real economic problems.Keyword:multicollinearity; diagnosis; remedial measures; stepwise regression; principal component regression;多重共线性是指模型中解释变量间存在相关关系。

习题1.下表给出了中国商品进口额Y 、国内生产总值GDP 、消费者价格指数CPI 。
年份 商品进口额 (亿元)国内生产总值(亿元)居民消费价格指数(1985=100)1985 1257.8 8964.4 1001986 1498.3 10202.2 106.5 1987 1614.2 11962.5 114.3 1988 2055.1 14928.3 135.8 1989 2199.9 16909.2 160.2 1990 2574.3 18547.9 165.2 1991 3398.7 21617.8 170.8 1992 4443.3 26638.1 181.7 1993 5986.2 34634.4 208.4 1994 9960.1 46759.4 258.6 1995 11048.1 58478.1 302.8 1996 11557.4 67884.6 327.9 1997 11806.5 74462.6 337.1 1998 11626.1 78345.2 334.4 1999 13736.4 82067.5 329.7 2000 18638.8 89468.1 331.0 2001 20159.2 97314.8 333.3 2002 24430.3 105172.3 330.6 200334195.6117251.9334.6资料来源:《中国统计年鉴》,中国统计出版社2000年、2004年。
请考虑下列模型:i t t t u CPI GDP Y ++=ln ln ln 321βββ+ (1)利用表中数据估计此模型的参数。
解:ln 3.6489 1.796ln 1.2075ln t t t Y GDP CPI =--+t= (-11.32) (9.93) (-3.415)20.988770.6.0.1124R F S E ===(2)你认为数据中有多重共线性吗?多重共线性的检验 1)综合统计检验法若 在OLS 法下:R 2与F 值较大,但t 检验值较小,则可能存在多重共线性。

计量经济学:多重共线性多重共线性52=.53085123 第四章专门讨论古典假定中⽆多重共线性假定被违反的情况,主要内容包括多重共线性的实质和产⽣的原因、多重共线性产⽣的后果、多重共线性的检测⽅法及⽆多重共线性假定违反后的处置⽅法。
第⼀节什么是多重共线性⼀、多重共线性的含义第三章讨论多元线性回归模型的估计时,强调了假定⽆多重共线性,即假定各解释变量之间不存在线性关系,或者说各解释变量的观测值之间线性⽆关。
在计量经济学中所谓的多重共线性(Multi-Collinearity),不仅包括解释变量之间精确的线性关系,还包括解释变量之间近似的线性关系。
从数学意义上去说明多重共线性,就是对于解释变量k X 、、X X 32,如果存在不全为0的数k λλλ,2,1 ,能使得n ,2, ,1i 033221 ==++++ki k i i X X X λλλλ ( 4.1 )则称解释变量k X X X ,,,32 之间存在着完全的多重共线性。
⽤矩阵表⽰,解释变量的数据矩阵为X=213112232223111k k nnkn X X X X X X X X X ??(4.2)当Rank(X )在实际经济问题中,完全的多重共线性并不多见。
常见的情形是解释变量k X X X ,,,32 之间存在不完全的多重共线性。
所谓不完全的多重共线性,是指对于解释变量k X 、、X X 32,存在不全为0的数k λλλ,2,1 ,使得n ,2, ,1i 033221 ==+++++i ki k i i u X X X λλλλ(4.3)其中,i u 为随机变量。
这表明解释变量k X 、、X X 32只是⼀种近似的线性关系。
如果k 个解释变量之间不存在完全或不完全的线性关系,则称⽆多重共线性。
若⽤矩阵4表⽰,这时X 为满秩矩阵,即Rank(X )=k 。
需要强调,解释变量之间不存在线性关系,并⾮不存在⾮线性关系,当解释变量存在⾮线性关系时,并不违反⽆多重共线性假定。

多重共线性的判断与修正一、多重共线性的判断1. 综合统计检验法LS Y C X1 X2 对模型进行OLS, 得到参数估计表(1) 当2,R F 很大,而回归系数的t 检验值小于临界值时,可判定该模型存在多重共线性。
(2) 当完全共线性存在时,模型的OLS 无法进行,Eviews 会提示:矩阵的逆(1()T X X -)不存在。
2. 简单相关系数检验法LS Y C X1 X2 对模型进行OLS, 得到参数估计表中的2R .点击:Quick/Group Statistics/Correlation在对话框中输入:X1 X2 , 点击OK, 即可得到简单相关系数矩阵检验:若存在 i j x x r 接近于1, 或 22,i j x x r R >,则说明,i j x x 之间存在着严重的相关性。
3. 辅助回归法(方差扩大因子法)设 121112...(1)(1)...j j k Xj X X X j X j Xk V ααααα-+=+++-+++++ (j ) LS Xj X1 X2…Xk 对(j) 进行OLS, 得到参数估计表检验:若表中 (2,1)F F k n k α>--+, 则可确定存在多重共线性。
或者(方差扩大因子法):计算211j jVIF R =-, (2j R 为以上方程的可决系数), 若10j VIF ≥, 则可确定存在多重共线性。
4. 逐步回归法1) 首先计算被解释变量对每个解释变量的回归方程,得到基本回归方程:LS Y C Xi OLS ,得到基本回归方程(i), i = 1,2,…,k2) 从这些基本回归方程中选出最合理的方程, 即,2R 取值最大,且t 检验显著。
比方说,0j Y Xj ββ=+3) 在这个选出的方程中增加新的解释变量, 再进行OLS 分析:LS Y C Xj Xi ( i= 1,2,…,j-1, j+1,…k)判断: 如果新加入的解释变量对2R 改进最大, 且每个系数又是t 统计显著,则保留这个新的解释变量。

时间 地点 实验题目 多重共线性的诊断与修正一、实验目的与要求:要求目的:1、对多元线性回归模型的多重共线性的诊断;2、对多元线性回归模型的多重共线性的修正。
二、实验内容根据书上第四章引子“农业的发展反而会减少财政收入”,1978-2007年的财政收入,农业增加值,工业增加值,建筑业增加值等数据,运用EV 软件,做回归分析,判断是否存在多重共线性,以及修正。
三、实验过程:(实践过程、实践所有参数与指标、理论依据说明等)(一)模型设定及其估计经分析,影响财政收入的主要因素,除了农业增加值,工业增加值,建筑业增加值以外,还可能与总人口等因素有关。
研究“农业的发展反而会减少财政收入”这个问题。
设定如下形式的计量经济模型:i Y =1β+2β2X +3β3X +4β4X +5β5X +6β6X +7β7X +i μ其中,i Y 为财政收入CS/亿元;2X 为农业增加值NZ/亿元;3X 为工业增加值GZ/亿元;4X 为建筑业增加值JZZ/亿元;5X 为总人口TPOP/万人;6X 为最终消费CUM/亿元;7X 为受灾面积SZM/千公顷。
图1: 1978~2007年财政收入及其影响因素数据年份财政收入CS/亿元 农业增加值NZ/亿元 工业增加值GZ/亿元 建筑业增加值JZZ/亿元总人口TPOP/万人最终消费CUM/亿元受灾面积SZM/千公顷 1978 1132.3 1027.5 1607 138.2 96259 2239.1 50790 1979 1146.4 1270.2 1769.7 143.8 97542 2633.7 39370 1980 1159.9 1371.6 1996.5 195.5 98705 3007.9 44526 1981 1175.8 1559.5 2048.4 207.1 100072 3361.5 39790 1982 1212.3 1777.4 2162.3 220.7 101654 3714.8 33130 1983 1367 1978.4 2375.6 270.6 103008 4126.4 34710 1984 1642.9 2316.1 2789 316.7 104357 4846.3 31890 1985 2004.8 2564.4 3448.7 417.9 105851 5986.3 44365 1986 2122 2788.7 3967 525.7 107507 6821.8 47140 1987 2199.4 3233 4585.8 665.8 109300 7804.6 42090 1988 2357.2 3865.4 5777.2 810 111026 9839.5 50870 1989 2664.9 4265.9 6484 794 112704 11164.2 46991 1990 2937.1 5062 6858 859.4 114333 12090.5 38474 1991 3149.48 5342.2 8087.1 1015.1 115823 14091.9 55472 1992 3483.37 5866.6 10284.5 1415 117171 17203.3 51333 1993 4348.95 6963.8 14188 2266.5 118517 21899.9 48829 19945218.1 9572.7 19480.7 2964.7 11985029242.2550431995 6242.2 12135.8 24950.6 3728.8 121121 36748.2 45821 1996 7407.99 14015.4 29447.6 4387.4 122389 43919.5 46989 1997 8651.14 14441.9 32921.4 4621.6 123626 48140.6 53429 1998 9875.95 14817.6 34018.4 4985.8 124761 51588.2 50145 1999 11444.08 14770 35861.5 5172.1 125786 55636.9 49981 2000 13395.23 14944.7 40036 5522.3 126743 61516 54688 2001 16386.04 15781.3 43580.6 5931.7 127627 66878.3 52215 2002 18903.64 16537 47431.3 6465.5 128453 71691.2 47119 2003 21715.25 17381.7 54945.5 7490.8 129227 77449.5 54506 2004 26396.47 21412.7 65210 8694.3 129988 87032.9 37106 2005 31649.29 22420 76912.9 10133.8 130756 96918.1 38818 2006 38760.2 24040 91310.9 11851.1 131448 110595.3 41091 2007 51321.78 28095 107367.2 14014.1 132129 128444.6 48992利用EV 软件,生成i Y 、2X 、3X 、4X 、5X 、6X 、7X 等数据,采用这些数据对模型进行OLS 回归。
试述多重共线性(统计累赘)的概念、特征及其测量方式和处理方式。
1、概念多重共线性是指自变量之间存在线性相关关。
倘若其中两个自变项的关系特别强,则在相互控制后就会使每者的效果减弱,而其他的变相的效果就会因此而增大。
2、特征3、产生原因产生多重相关性的原因主要包括四方面。
一是没有足够多的样本数据; 二是选取的自变量之间客观上就有共线性的关系; 还可能由其它因素导致, 如数据采集所用的方法, 模型设定, 一个过度决定的模型等。
但多数研究者认为共线性本质上是由于样本数据不足引起的。
4、测量方式(1)经验式的诊断方法通过观察,得到一些多重相关性严重存在的迹象。
①在自变量的简单相关系数矩阵中,有某些自变量的相关系数值较大。
②回归系数的代数符号与专业知识或一般经验相反;或者该自变量与因变量的简单相关系数符号相反。
③对重要自变量的回归系数进行t 检验,其结果不显著。
特别是当F 检验能在高精度下通过,测定系数R 2的值也很大,但自变量的t 检验却全都不显著,这时多重相关性的可能将会很大。
④如果增加或删除一个变量,或者增加或删除一个观测值,回归系数发生了明显的变化。
⑤重要自变量的回归系数置信区别明显过大。
⑥在自变量中,某一个自变量是另一部分自变量的完全或近似完全的线性组合。
⑦对于一般的观测数据,如果样本点的个数过少,比如接近于变量的个数或者少于变量的个数,样本数据中的多重相关性就会经常存在。
(2)统计检验方法共线性的诊断方法是基于对自变量的观测数据构成的矩阵X ’X 进行分析,使用各种反映自变量间相关性的指标。
共线性诊断常用的统计量有方差膨胀因子VIF 或容限TOL 、条件指数和方差比例等。
方差膨胀因子VIF 是指回归系数的估计量由于自变量的共线性使其方差增加的一个相对度量。
对于第i 个回归系数,它的方差膨胀因子定义为:VIF=1/1-R 2=1/TOL i 其中R2i 是自变量Xi 对模型中其余自变量线性回归模型的R 平方。
多重共线性诊断及处理⼀、定义多重共线性(Multicollinearity)是指线性回归模型中的解释变量之间由于存在较精确相关关系或⾼度相关关系⽽使模型估计失真或难以估计准确。
完全共线性的情况并不多见,⼀般出现的是在⼀定程度上的共线性,即近似共线性。
⼆. ⽬前常⽤的多重共线性诊断⽅法 1.⾃变量的相关系数矩阵R诊断法:研究变量的两两相关分析,如果⾃变量间的⼆元相关系数值很⼤,则认为存在多重共线性。
但⽆确定的标准判断相关系数的⼤⼩与共线性的关系。
有时,相关系数值不⼤,也不能排除多重共线性的可能。
R实现:画协⽅差矩阵图 2.⽅差膨胀因⼦(the variance inflation factor,VIF)诊断法:⽅差膨胀因⼦表达式为:VIFi=1/(1-R2i)。
其中Ri为⾃变量xi对其余⾃变量作回归分析的复相关系数。
当VIFi很⼤时,表明⾃变量间存在多重共线性。
该诊断⽅法也存在临界值不易确定的问题,在应⽤时须慎重。
判断:VIF j>10时,说明⾃变量x与其余⾃变量之间存在严重的多重共线关系,这种多重共线性可能会过度地影响最⼩⼆乘估计值 3.容忍值(Tolerance,简记为Tol)法:容忍值实际上是VIF的倒数,即Tol=1/VIF。
其取值在0~1之间,Tol越接近1,说明⾃变量间的共线性越弱。
在应⽤时⼀般先预先指定⼀个Tol值,容忍值⼩于指定值的变量不能进⼊⽅程,从⽽保证进⼊⽅程的变量的相关系数矩阵为⾮奇异阵,计算结果具有稳定性。
但是,有的⾃变量即使通过了容忍性检验进⼊⽅程,仍可导致结果的不稳定。
4.多元决定系数值诊断法:假定多元回归模型p个⾃变量,其多元决定系数为R2y(X1,X2,…,Xp)。
分别构成不含其中某个⾃变量(Xi,i=1,2,…,p)的p个回归模型,并应⽤最⼩⼆乘法准则拟合回归⽅程,求出它们各⾃的决定系数R2i(i=1,2,…,p)。
如果其中较⼤的⼀个R2k与R2y很接近,就表明该⾃变量在模型中对多元决定系数的影响不⼤,说明该变量对Y总变异的解释能⼒可由其他⾃变量代替。
数学与统计学院实验报告院(系):数学与统计学学院 学号: 姓名: 实验课程: 计量经济学 指导教师:实验类型(验证性、演示性、综合性、设计性): 综合性 实验时间:2017年 4 月 5 日 一、实验课题多重共线性的诊断及处理 二、实验目的和意义第8周练习 多重共线性右表是某城市财政收入rev 、第一、第二、第三产业gdp1、gdp2、gdp3的有关数据。
1).建立rev 对gdp1,gdp2,gdp3的多元线性回归,并从经济和数理统计上简要说明模型存在着哪些不足。
2).写出rev ,gdp1,gdp2,gdp3的相关系数矩阵。
3).利用判别系数法判断模型是否存在着多重共线性。
4).用逐步回归的方法排除引起共线性的变量,重新建立多元回归。
5).如果不想排除变量,通过经验,假设:gdp1对财政收入的贡献是 gdp3的三倍,而且gdp2与财政收入是对数线性关系。
那么请建立ln (rev )对(3gdp1+gdp3)及ln (gdp2)的半对数线性回归模型,看看模型在经济和数学上是否合理,并从中你得到了什么启示(自己随意发挥)。
三、解题思路(eviews6)1、建立多元线性回归:quick —estimate equation —(rev c gdp1 gdp2 gdp3)年份 rev gdp1 gdp2 gdp3 1983 6604 27235 26781 7106 1984 6634 26680 28567 10240 1985 6710 26762 31766 11912 1986 6823 33595 40062 14160 1987 8103 38510 52935 16960 1988 8578 41529 61337 18777 1989 8469 47994 67848 30498 1990 11118 65138 98946 39700 1991 16053 86983 112531 66960 1992 20221 105825 143545 92231 1993 27076 129136 223697 117031 1994 31888 138619 216161 151334 1995 35139 146637 305940 193573 1996 42436 149788 371066 227561 1997 56204 161800 426925 256684 1998 93828 162960 614341 372177 1999 130532 199519 821302 524562 200017906324664811210586885672、建立相关系数矩阵:quick--group statistic--correlation--rev gdp1 gdp2 gdp3)3、判定系数法:利用一解释变量由其他解释变量变出模型一::quick—estimate equation—(gdp1 c gdp2 gdp3)模型二::quick—estimate equation—(gdp2 c gdp1 gdp3)模型三::quick—estimate equation—(gdp3 c gdp1gdp2)4、逐步回归:quick—estimate equation—method:stepwise—rev c- gdp1 gdp2 gdp35、建立对数线性关系:quick—estimate equation—LOG(REV) C3*GDP1+GDP3 LOG(GDP2)四、实验过程记录与结果1、建立多元回归方程:模型:REV = 7726.69598122 - 0.180508326923*GDP1 + 0.0759120320555*GDP2 + 0.185205459439*GDP3通过多元回归模型可见,该模型通过假设检验,但是两个解释变量的效果并不好(p>0.05);第二点是GDP1表示第一产业,不存在负值,所以不满足经济条件2、相关系数矩阵:(3、判定系数法:(利用一解释变量由其他解释变量变出,检验拟合优度)由系数判定法,可以看出三个模型都显著性成立,即任意一个解释变量都能由其他解释变量线性变出,所以可以得出该模型存在多重共线性。
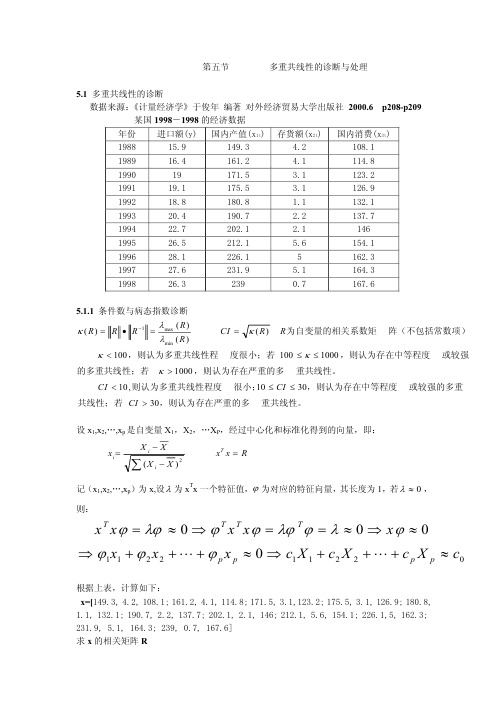
第五节 多重共线性的诊断与处理5.1 多重共线性的诊断 数据来源:《计量经济学》于俊年 编著 对外经济贸易大学出版社 2000.6 p208-p2095.1.1 条件数与病态指数诊断重共线性。
,则认为存在严重的多共线性;若或较强的多重,则认为存在中等程度很小;则认为多重共线性程度重共线性。
,则认为存在严重的多的多重共线性;若或较强,则认为存在中等程度度很小;若,则认为多重共线性程阵(不包括常数项)为自变量的相关系数矩303010,1010001000100100)()()()(min max 1>≤≤<>≤≤<==•=-CI CI CI R R CI R R R R R κκκκλλκ设x 1,x 2,…,x p 是自变量X 1,X 2,…X P ,经过中心化和标准化得到的向量,即:R x x X XXX x T ii i =--=∑2)(记(x 1,x 2,…,x p )为x,设λ为x T x 一个特征值,ϕ为对应的特征向量,其长度为1,若0≈λ,则:221122110000c X c X c X c x x x x x x x x p p p p T T T T ≈+++⇒≈+++⇒≈⇒≈==⇒≈= ϕϕϕϕλϕλϕϕϕλϕϕ根据上表,计算如下: x=[149.3, 4.2, 108.1; 161.2, 4.1, 114.8; 171.5, 3.1,123.2; 175.5, 3.1, 126.9; 180.8, 1.1, 132.1; 190.7, 2.2, 137.7; 202.1, 2.1, 146; 212.1, 5.6, 154.1; 226.1,5, 162.3; 231.9, 5.1, 164.3; 239, 0.7, 167.6] 求x 的相关矩阵RR=corrcoef(x) R =1.00000000000000 0.02447049083573 0.99715218582079 0.02447049083573 1.00000000000000 0.03567322292007 0.99715218582079 0.03567322292007 1.00000000000000求R 的条件数: cond(R) ans =7.178039564809832e+002 也可先求R 的特征值 e=eig(R) e =0.00278483106125 0.99825241504342 1.99896275389533 注:3自变量的个数==∑e e(3)/e(1)ans =7.178039564809491e+002条件数为717.804,大于100,存在较严重的多重共线性。
为了进一步了解哪些变量之间存在线性关系,计算相关矩阵的特征值和相应的特征向量: [v,d]=eig(R) v =0.70696453896575 0.03569873579633 0.70634746471371 0.00795062868633 -0.99906334219563 0.04253499482058 -0.70720430439049 0.02445482658777 0.70658618250581 d =0.00278483106125 0 0 0 0.99825241504342 0 0 0 1.99896275389533 注意:Rv=vd v 为标准正交矩阵最小的特征值为0.00278483106125,对应的向量为:(0.70696453896575,0.00795062868633,-0.70720430439049)T 考虑到第二个数0.00795062868633约等于0,从而 即:07072.0707.031≈-x x 所以存在310,,c c c 使得:03211c x c x c ≈+5.1.2 方差膨胀因子诊断每一个自变量对应的方差膨胀因子为R -1相应的对角元素r jj 。
若记x j 关于其他p-1个自变量的复相关系数为R j 则有:}{m ax 112jj jjjjr VIF R r=-=如果VIF<5,则认为自变量间不存在多重共线性。
如果性。
程度或较强的多重共线就认为自变量间存中等,105≤≤VIF如果VIF>10,则认为自变量间存在严重的多重共线性。
在本例中: diag(inv(R)) ans =1.0e+002 *1.79722747043643 0.01023478872590 1.79843993838056 VIF=max(diag(inv(R))) VIF =1.798439938380555e+002VIF 远大于10,存在严重的多重共线性。
注意:书上结果错了,我用SPSS 算了,也是这个结果。
方差膨胀因子也可按此计算:x1=x(:,1);x2=x(:,2);x3=x(:,3); [b bint,r,rint,stats]=regress(x1,[ones(11,1) x2 x3]);一定要常数项1/(1-stats(1)) ans =1.797227470435788e+0025.1.3 容许度(Tolerance)诊断若记x j 关于其他p-1个自变量的复相关系数为R j 则有:Tol j =1-R 2j它是方差膨胀化因子的倒数。
越小自变量共线性越强。
小于0.1高度共线 在本例中:Tol=1./diag(inv(R)) Tol =0.00556412594649 0.97705973887803 0.00556037473734最小的值远小0.1,高度多重共线性。
5.1.4 方差比例诊断(看Applied Econometric using Matlab 的第84页)注意:Applied Econometric using Matlab的第84页,4.4式是错的,4.3,4.5,4.6式是对的。
某国1998-1998的经济数据x1=[149.3, 4.2, 108.1; 161.2, 4.1, 114.8; 171.5, 3.1,123.2; 175.5, 3.1, 126.9; 180.8, 1.1, 132.1; 190.7, 2.2, 137.7; 202.1, 2.1, 146; 212.1, 5.6, 154.1; 226.1,5, 162.3; 231.9, 5.1, 164.3; 239, 0.7, 167.6];x=[ones(size(x1,1),1),x1];vnames=strvcat('constant','x1','x2','x3');fmt='%12.6f';bkw(x,vnames,fmt);Belsley, Kuh, Welsch Variance-decompositionK(x) constant x1 x2 x31 0.000000 0.000051 0.000000 0.000012140 0.000006 0.140284 0.598136 0.116948188 0.000011 0.680208 0.375680 0.6462631978 0.999983 0.179457 0.026184 0.236777K(x)=188时,有两个方差比例大于0.5,x1与x3可以存在共线性。
K(X)>30 或者方差比例>0.5,则存在多重共线性。
上表的算法:[nobs nvar] = size(x);[u d v] = svd(x,0);lamda = diag(d(1:nvar,1:nvar));lamda2 = lamda.*lamda;v = v.*v;phi = zeros(nvar,nvar);for i=1:nvar;phi(i,:) = v(i,:)./lamda2';end;pi = zeros(nvar,nvar);for i=1:nvar;phik = sum(phi(i,:));pi(i,:) = phi(i,:)/phik;end;pi'ans =0.00000000000428 0.00005121386618 0.00000000753568 0.000012482052740.00000606371588 0.14028373758356 0.59813616157856 0.116947537521540.00001066784928 0.68020848180663 0.37568029573565 0.646262520841230.99998326843056 0.17945656674363 0.02618353515011 0.23677745958449K(x)的算法:[u d v] = svd(x,0);d1=diag(d);d1 =1.0e+002 *8.028370999629810.057460066311730.042602312882930.00405906633001kx=[d1(1)/d1(1);d1(1)/d1(2);d1(1)/d1(3);d1(1)/d1(4)]kx =1.0e+003 *0.001000000000000.139720879472630.188449181660431.977886131170545.2 多重共线性的处理可参见《经济计量学》李景华编著中国商业出版社第四章5.2.1x=[149.3, 4.2, 108.1; 161.2, 4.1, 114.8; 171.5, 3.1,123.2; 175.5, 3.1, 126.9; 180.8, 1.1, 132.1; 190.7, 2.2, 137.7; 202.1, 2.1, 146; 212.1, 5.6, 154.1; 226.1,5, 162.3; 231.9, 5.1, 164.3; 239, 0.7, 167.6];y=[15.9; 16.4;19;19.1; 18.8; 20.4; 22.7; 26.5; 28.1; 27.6; 26.3];bb = zeros(4,101);kvec = 0:0.01:1;count = 0;for k = 0:0.01:1b(:,count) = ridge(y,[ones(11,1) x],k);endplot(kvec',b'),xlabel('k'),ylabel('b','FontName','Symbol')βk点击最上面一要线,删除得:βk如果不想在图中包括常数项,则可:bb = zeros(3,101);kvec = 0:0.01:1;count = 0;for k = 0:0.01:1count = count + 1;bb(:,count) = ridge(y, x,k);endplot(kvec',bb'),xlabel('k'),ylabel('b','FontName','Symbol')βk为了看清k在0到0.1之间回归系数的变化情况,则:bb = zeros(3,11);kvec = 0:0.01:0.1;count = 0;for k = 0:0.01:0.1count = count + 1;bb(:,count) = ridge(y, x,k);endplot(kvec',bb'),xlabel('k'),ylabel('b','FontName','Symbol')βk因此,在k=0.04,各回归系数基本稳定。