当前位置：文档之家 › 计量经济学-7章：多重共线性

计量经济学-7章：多重共线性

  • 格式：ppt
  • 大小：1.37 MB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

7.1多重共线性的概念及产生原因

7.1多重共线性的概念及产生原因

第一节多重共线性的概念及产生原因第二节多重共线性的后果第三节多重共线性的检验第四节多重共线性的修正方法第五节案例分析第一节多重共线性的概念及产生原因多重共线性产生的原因对于k元线性回归模型如果模型的解释变量之间存在着较强的相关关系则称模型存在多重共线性
第七章 多重共线性
• 本章主要内容： 本章主要内容： 第一节 多重共线性的概念及产生原因 第二节 多重共线性的后果 第三节 多重共线性的检验 第四节 多重共线性的修正方法 第五节 案例分析
多重共线性有两种情况： 多重共线性有两种情况：完全多重共线性和 近似多重共线性。 近似多重共线性。
如果存在一组不全为零的数λ0 , λ1 , λ2 ,⋯ , λk，使得
λ0 + λ1 X 1i + λ2 X 2i + ⋯ + λk X ki = 0
则称模型存在完全多重共线性。 则称模型存在完全多重共线性。 完全多重共线性
（2）解释变量中含有滞后变量 ） 在计量经济学模型中， 在计量经济学模型中，往往需要引入滞后经济 变量来反映真实的经济关系。例如，以相对收入 变量来反映真实的经济关系。例如， 假说为理论假设，则居民消费C 假说为理论假设，则居民消费 t的变动不仅受当 期收入Y 的影响， 的影响， 期收入 t的影响，还受前期收入 Yt-1的影响，于 是建立以下模型： 是建立以下模型：
Ct = β 0 + β1Yt + β 2Yt −1 + ut
显然， 显然，当期收入和前期收入之间存在着较强的线 性相关性。 性相关性。
3.利用截面数据建立模型也可能出现多重共线性 利用截面数据建立模型也可能出现多重共线性 多重共线性一般与时间序列有关， 多重共线性一般与时间序列有关，但在截面 一般与时间序列有关 数据中也经常出现。例如，在生产函数中， 数据中也经常出现。例如，在生产函数中，大企 业拥有大量的劳动力和资本，小企业只有较少的 业拥有大量的劳动力和资本， 劳动力和资本， 劳动力和资本，投入的劳动量和资本量通常是高 度相关的。 度相关的。 在多元线性回归模型中， 在多元线性回归模型中，我们关心的并不是 多重共线性的有无，而是多重共线性的程度。当 多重共线性的有无，而是多重共线性的程度。 有无 程度 多重共线性程度过高时， 多重共线性程度过高时，将给最小二乘估计带来 严重的后果。 严重的后果。
计量经济学：多重共线性

计量经济学：多重共线性

计量经济学：多重共线性多重共线性52=.53085123 第四章专门讨论古典假定中⽆多重共线性假定被违反的情况，主要内容包括多重共线性的实质和产⽣的原因、多重共线性产⽣的后果、多重共线性的检测⽅法及⽆多重共线性假定违反后的处置⽅法。

第⼀节什么是多重共线性⼀、多重共线性的含义第三章讨论多元线性回归模型的估计时，强调了假定⽆多重共线性，即假定各解释变量之间不存在线性关系，或者说各解释变量的观测值之间线性⽆关。

在计量经济学中所谓的多重共线性(Multi-Collinearity)，不仅包括解释变量之间精确的线性关系，还包括解释变量之间近似的线性关系。

从数学意义上去说明多重共线性，就是对于解释变量k X 、、X X 32，如果存在不全为0的数k λλλ,2,1 ，能使得n ,2, ,1i 033221 ==++++ki k i i X X X λλλλ ( 4.1 )则称解释变量k X X X ,,,32 之间存在着完全的多重共线性。

⽤矩阵表⽰，解释变量的数据矩阵为X=213112232223111k k nnkn X X X X X X X X X ??（4.2）当Rank(X )在实际经济问题中，完全的多重共线性并不多见。

常见的情形是解释变量k X X X ,,,32 之间存在不完全的多重共线性。

所谓不完全的多重共线性，是指对于解释变量k X 、、X X 32，存在不全为0的数k λλλ,2,1 ，使得n ,2, ,1i 033221 ==+++++i ki k i i u X X X λλλλ（4.3）其中,i u 为随机变量。

这表明解释变量k X 、、X X 32只是⼀种近似的线性关系。

如果k 个解释变量之间不存在完全或不完全的线性关系，则称⽆多重共线性。

若⽤矩阵4表⽰，这时X 为满秩矩阵，即Rank(X )=k 。

需要强调，解释变量之间不存在线性关系，并⾮不存在⾮线性关系，当解释变量存在⾮线性关系时，并不违反⽆多重共线性假定。

计量经济学07计量多重共线性

计量经济学07计量多重共线性


Y/C1 △ Y
0.6072 0.6028 0.5996 0.5613 0.5339 0.5697
588 587 1088 1628 1441
0.5552 1651 0.5067 2920
0.5684 1762 0.5762 1854 0.5339 2960 0.5083 4584 0.4624 8637 0.4284 12610 0.4581 12294 0.5041 9093
横截面数据：生产函数中，资本投入与劳动力投入往 往出现高度相关情况，大企业二者都大，小企业都小。
（2）滞后变量的引入
在经济计量模型中，往往需要引入滞后经济变量来 反映真实的经济关系。例如消费变动的影响因素不仅有 本期可支配收入，还应考虑以往各期的可支配收入；固 定资产存量变动的影响因素不仅有本期投资，还应考虑 以往若干期的投资。同一变量的前后期之值很可能有较 强的线性相关性，模型中引入了滞后变量，多重共线性 就难以避免。
第七章 多重共线性
（Multicollinearity）
一、多重共线性的概念 二、实际经济问题中的多重共线性 三、多重共线性的后果 四、多重共线性的检验 五、克服多重共线性的方法 六、案例
一、多重共线性的概念
对于模型
Yi= 0+ 1X1i+ 2X2i+ + kXki+ i
i=1,2,…,n 其基本假设之一是解释变量是互相独立的。
求出X1与X2的简单相关系数r，若|r|接近1，则说明两变量 存在较强的多重共线性。
(2) 对多个解释变量的模型，采用综合统计检验法
若 在OLS法下：R2与F值较大，但t检验值较小，说明各 解释变量对Y的联合线性作用显著，但各解释变量间存在共 线性而使得它们对Y的独立作用不能分辨，故t检验不显著。
多重共线性检验方法

多重共线性检验方法

多重共线性检验方法
多重共线性检验方法是检验自变量之间是否存在强相关性的一种方法。

共线性可能导致回归结果不可靠，误差增加，对自变量的解释力下降等问题。

因此，进行多重共线性检验是回归分析中非常重要的一环。

常见的多重共线性检验方法包括变量间的相关系数、方差膨胀因子（VIF）和特征值等。

变量间的相关系数可以通过计算自变量两两之间的皮尔逊相关系数来得到。

如果相关系数大于0.8或0.9，可以认为自变量之间存在强相关性。

方差膨胀因子（VIF）是用来度量自变量间线性关系强度的一种方法。

VIF越大，表示自变量与其他自变量之间的相关性越强。

特征值检验是对协方差矩阵进行特征值分解，通过判断特征值的大小来确定自变量之间的共线性程度。

如果存在特征值较小的情况，可以表明存在多重共线性。

此外，还有其他一些检验方法，如条件数、扰动法等，可以用来检验多重共线性。

综上所述，多重共线性检验是回归分析中重要的一步，通过各种方法来判断自变量之间是否存在强相关性，以保证回归模型的稳健性和可靠性。

计量经济学4-7章单选、多选题带答案

计量经济学4-7章单选、多选题带答案


18、设 x1 , x2 为解释变量，则完全多重共线性是（ A ）
1 A.x12x2 0
B.x1ex2 0
C.x11 2x2v0(v为随机误差 D.x1 项 ex2 ） 0
19、多重共线性是一种（ A
A、样本现象
C．被解释变量现象
） B.随机误差现象
D.总体现象
20、广义差分法是对（
A .y t 1 2 x t u t C .y t 1 2 x t u t
B . fy(ixi)f(1 xi)2
xi ui f(xi) f(xi)
D .yif(xi)1f(xi)2xif(xi)uif(xi)
45、对模型进行对数变换,其原因是（ B ）
A.能使误差转变为绝对误差 B.能使误差转变为相对误差. C.更加符合经济意义 D.大多数经济现象可用对数模型表示
46、在修正异方差的方法中，不正确的是（ D ）
A. 广义差分法 C. 普通最小二乘法
）的一个特例 B. 广义最小二乘法. D. 两阶段最小二乘法
25、设 i 为随机误差项，则一阶自相关是指（ B ）
A .co t,s v ) 0 ((t s)
B .u tu t 1t
C .u t2 6、1 在u t序 1 列 自2 相u t关 2 的 情t况下，参数估计值D 仍.u 是t无 偏2 的u t， 1 其 原t因
B. Cochrane-Orcutt法 D. 移动平均法
36、违背零均值假定的原因是（
A.变量没有出现异常值
B
.
C.变量为正常波动
） B.变量出现了异常值
D.变量取值恒定不
37、在下列多重共线性产生的原因中，不正确的是（ D ）
A. 经济变量大多存在共同变化趋势 B. 模型中大量采用滞后变量 C. 由于认识上的局限使得选择变量不当 D. 解释变量与随机误差项相关.
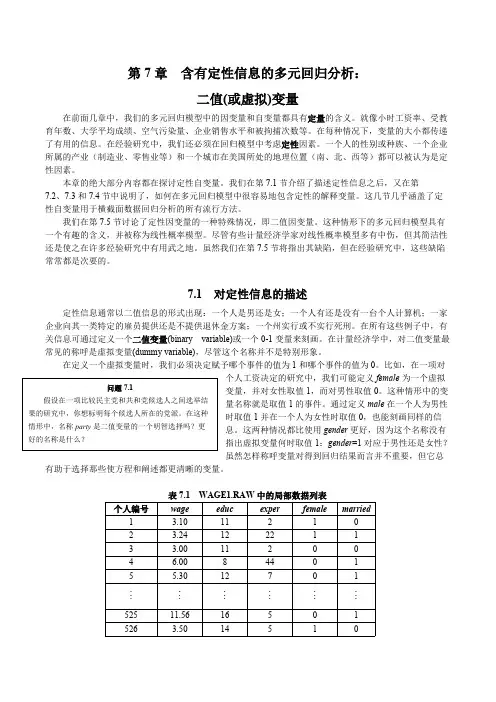
计量经济学第7章含有定性信息的多元回归分析

计量经济学第7章含有定性信息的多元回归分析

第7章含有定性信息的多元回归分析：二值(或虚拟)变量在前面几章中，我们的多元回归模型中的因变量和自变量都具有定量的含义。

就像小时工资率、受教育年数、大学平均成绩、空气污染量、企业销售水平和被拘捕次数等。

在每种情况下，变量的大小都传递了有用的信息。

在经验研究中，我们还必须在回归模型中考虑定性因素。

一个人的性别或种族、一个企业所属的产业（制造业、零售业等）和一个城市在美国所处的地理位置（南、北、西等）都可以被认为是定性因素。

本章的绝大部分内容都在探讨定性自变量。

我们在第7.1节介绍了描述定性信息之后，又在第7.2、7.3和7.4节中说明了，如何在多元回归模型中很容易地包含定性的解释变量。

这几节几乎涵盖了定性自变量用于横截面数据回归分析的所有流行方法。

我们在第7.5节讨论了定性因变量的一种特殊情况，即二值因变量。

这种情形下的多元回归模型具有一个有趣的含义，并被称为线性概率模型。

尽管有些计量经济学家对线性概率模型多有中伤，但其简洁性还是使之在许多经验研究中有用武之地。

虽然我们在第7.5节将指出其缺陷，但在经验研究中，这些缺陷常常都是次要的。

7.1 对定性信息的描述定性信息通常以二值信息的形式出现：一个人是男还是女；一个人有还是没有一台个人计算机；一家企业向其一类特定的雇员提供还是不提供退休金方案；一个州实行或不实行死刑。

在所有这些例子中，有关信息可通过定义一个二值变量(binary variable)或一个0-1变量来刻画。

在计量经济学中，对二值变量最常见的称呼是虚拟变量(dummy variable)，尽管这个名称并不是特别形象。

在定义一个虚拟变量时，我们必须决定赋予哪个事件的值为1和哪个事件的值为0。

比如，在一项对个人工资决定的研究中，我们可能定义female 为一个虚拟变量，并对女性取值1，而对男性取值0。

这种情形中的变量名称就是取值1的事件。

通过定义male 在一个人为男性时取值1并在一个人为女性时取值0，也能刻画同样的信息。

多重共线性名词解释

多重共线性名词解释

多重共线性名词解释多重共线性多重共线性，是指同一条曲线在不同时期反映了同一经济行为。

从外部看来，这些具有相同特征或因素的影响在不同的经济行为中是互不相关的。

但是，这些事物之间却存在着内在联系：外在表象或因素之间存在的线性关系可以用一个概念进行解释，就是说，事物在不同时期的不同影响因素是有机整体。

从更广泛的意义上说，每一个影响因素都具有相同的行为，并且，与其他影响因素有机地结合起来，构成一个统一的模式，而该模式又反过来对另一类型的影响因素产生决定性的影响。

11、地方政府支出变动； 12、总统选举（赢者通吃）； 13、结构变迁，也叫结构演化； 14、创新系统； 15、全球化； 16、文化遗产。

2、现代主义的城市设计理念，将都市视为由“住宅区—商业区—工业区”三部分组成的体系。

3、城市设计必须考虑城市空间的问题，即研究如何使人们的生活活动与各种建筑要素、城市的生态环境之间保持协调和融洽，从而达到舒适、安全、健康、卫生和高效率的目的。

4、城市形象是城市的面子。

5、美国城市设计师查尔斯·罗奇(Charles Lorich)最早提出这个概念，认为当代城市不仅需要考虑功能、技术和经济的问题，而且还应考虑空间和社会层面的问题。

6、区域化导致市场分割。

7、超大城市化正在发展。

8、现代主义强调标准化、简约化和功能性，注重形式逻辑、数字技术和系统分析，因此在城市设计领域颇受推崇。

9、我国正处于城镇化快速发展阶段。

10、“城乡规划是一门为公众利益服务的艺术。

”6、区域化导致市场分割，尤其在资本积累时期。

城市边缘化现象严重。

7、目前的城市空间扩张伴随着高成本、高风险和高消耗。

8、现代主义空间追求便捷、开放和轻松。

9、城市结构理论的发展与新城市主义思潮的兴起。

10、美国城市设计师查尔斯·罗奇(Charles Lorich)最早提出这个概念，认为当代城市不仅需要考虑功能、技术和经济的问题，而且还应考虑空间和社会层面的问题。

计量经济学题库第7章多重共线性

计量经济学题库第7章多重共线性

第7章 多重共线性习 题一、单项选择题1．如果回归模型中解释变量之间存在完全的多重共线性，则最小二乘估计量（ ）A.不确定，方差无限大B.确定，方差无限大C.不确定，方差最小D.确定，方差最小2．多元线性回归模型中，发现各参数估计量的t 值都不显著，但模型的F 值确很显著，这说明模型存在（ ）A ．多重共线性B ．异方差C ．自相关D ．设定偏误 3．逐步回归法既检验又修正了（ ）A ．异方差性 B.自相关性 C ．随机解释变量 D.多重共线性4．如果模型中的解释变量存在完全的多重共线性，参数的最小二乘估计量是（ ）A ．无偏的 B. 有偏的 C. 不确定 D. 确定的 5．设线性回归模型为，下列表明变量之间具有完全多重共线性的是（ ）A ．B ．C ．D ．其中v 为随机误差项6．简单相关系数矩阵方法主要用于检验（ ）A ．异方差性 B.自相关性 C ．随机解释变量 D.多重共线性 7．设为解释变量，则完全多重共线性是( )8．下列说法不正确的是（ ）A. 多重共线性产生的原因有模型中大量采用滞后变量,)(22很大或R R 01122i i i iY X X u βββ=+++1202*0*0i i X X ++=1202*0*0i i X X v +++=1200*0*0i i X X ++=1200*0*0i i X X v +++=21,x x 221211211.0.021.0(.02x x A x x B x e C x x v v D x e +==++=+=为随机误差项）B. 多重共线性是样本现象C. 检验多重共线性的方法有DW检验法D. 修正多重共线性的方法有增加样本容量二、多项选择题1．能够检验多重共线性的方法有（）A. 简单相关系数矩阵法B. t检验与F检验综合判断法C. DW检验法D. ARCH检验法E. White 检验2．如果模型中解释变量之间存在共线性，则会引起如下后果（）A. 参数估计值确定B. 参数估计值不确定C. 参数估计值的方差趋于无限大D. 参数的经济意义不正确E. DW统计量落在了不能判定的区域3．能够检验多重共线性的方法有（）A. 简单相关系数矩阵法B. DW检验法C. t检验与F检验综合判断法D. ARCH检验法E. 辅助回归法(又待定系数法)三、判断题1．多重共线性问题是随机扰动项违背古典假定引起的。

计量经济学：多重共线性

计量经济学：多重共线性


影响比较大的，略去影响较小的。
元线性回归模型并进行OLS估计，拟合优度最大且接近1时，说明
这个变量与其他所有解释变量间存在共线性。
第三节 多重共线性的检验
辅助回归法中的方差膨胀因子：
对 于 多 元 线 性 回 归 模： 型Yi 0 1 X 1i ... k X ki ui 为 判 断 诸 自 变 量 间 是存 否在 多 重 共 线 性 ， 进如 行下 辅 助 回 归 ： X ji 0 1 X 1i ... j 1,i X j 1,i j 1,i X j 1,i ... k X ki v i , j 1,2,...,k 若 上 述 辅 助 回 归 的 可系 决数 为 R2 X j的 方 差 膨 胀 因 子 为 ： j， 则 定 义 自 变 量 1 VIF j 1 R2 j
第一节 多重共线性的概念
若有c0+c1X1i+c2X2i+…+ckXki=0 i=1,2,…,n。其中: ci不全为0，则称
解释变量间存在完全多重共线性
若存在：c0+c1X1i+c2X2i+…+ckXki≈0 i=1,2,…,n。 其中：ci不全为0，
则称为解释变量间存在近似多重共线性。
完全共线性的情况并不多见，一般出现的是在一定程度上的共线性，
第二节 多重共线性的来源与后果
4、参数估计值不稳定，经济含义不合理
样本观测值稍有变动、增加或减少解释变量等都会使参数估计值发生较大变 化，甚至出现符号错误，从而不能正确反映解释变量对被解释变量的影响。
5、模型的预测功能失效
较大的方差容易使预测区间变大，从而使预测失去意义
注意：只要模型满足经典假设，则在近似多重共线性情况下，OLS估计量仍 然满足无偏性、线性性和有效性。但此时，无偏性并不意味着对某一给定样 本，其参数估计值就等于真实值。有效性也不意味着参数估计量的方差一定 很小。
计量经济学复习资料——多重共线性习题

计量经济学复习资料——多重共线性习题

多重共线性一、单项选择题1、在线性回归模型中，若解释变量1X 和2X 的观测值成比例，既有12i i X kX =，其中k 为非零常数，则表明模型中存在（ ）A 、异方差B 、多重共线性C 、序列相关D 、随机解释变量2、对于模型01122i i i i Y X X βββμ=+++，与r 12=0相比，当r 12=0.15时，估计量1ˆβ的方差1ˆ()Var β将是原来的 （ ） A 、1倍 B 、1.023倍 C 、1.96倍 D 、2倍3、如果方差膨胀因子VIF=15，则认为（ ）问题是严重的A 、异方差问题B 、序列相关问题C 、多重共线性问题D 、解释变量与随机项的相关性4、不完全多重共线性下参数估计量 （ ）A 、不存在B 、有无穷多解C 、唯一D 、非有效5、完全多重共线性下参数估计量 （ ）A 、唯一B 、有无穷多解C 、不存在D 、有效6、下列方法中，可克服多重共线性的是（ ）A 、差分法B 、加权最小二乘法C 、工具变量法D 、广义最小二乘法7、对于模型01t t t y b b x u =++，为了考虑“地区”因素（北方、南方），引入2个虚拟变量形成截距变动模型，则会产生（ ）。

A.序列的完全相关B.序列不完全相关C.完全多重共线性D.不完全多重共线性二、多项选择题1、多重共线性产生的主要原因有 （ ）A 、经济变量之间往往存在同方向的变化趋势B 、经济变量之间往往存在密切的关联度C 、在模型中采用滞后变量也容易产生多重共线性D 、样本数据变异范围过小2、检验多重共线性严重性的方法有 （ ）A 、等级相关系数法B 、方差膨胀因子C 、工具变量法D 、判定系数检验法E 、逐步回归法3、当模型中解释变量间存在高度的多重共线性时 （ ）A 、各个解释变量对被解释变量的影响将难于精确鉴别B 、部分解释变量与随机干扰项之间将高度相关C 、估计量的精确度大幅下降D 、估计量对于样本容量的变动将十分敏感E 、模型的随机误差项也将序列相关4、多重共线性解决方法主要有 （ ）A 、保留重要的解释变量，去掉次要的或可替代的解释变量B 、利用先验信息改变参数的约束形式C 、变换模型的形式D 、综合使用时间数据与截面数据E 、逐步回归法以及增加样本容量三、判断题1、当用于检验方程线性显著性的F 统计量与检验单个系数显著性的t 统计量结果矛盾时可以认为出现了严重的多重共线性（ ）2、当存在严重的多重共线性时，普通最小二乘法往往会低估参数估计量的方差 （ ）3、变量的两两高度相关并不表示高度多重共线性，变量不存在两两高度相关表示不存在高度多重共线性（ ）4、由于多重共线性不会影响到随机干扰项的方差，因此如果分析的目的仅仅是预测，则可以容忍一定程度多重共线性 （ ）5、考虑以下回归模型：i i i i i u X X X Y ++++=332210ββββ，由于三各解释变量之间存在明显的函数关系，因此该模型肯定具有多重共线性 （ ）6、尽管存在多重共线性，OLS 估计量依然是BLUE （ ）。

计量经济学4.3多重共线性

计量经济学4.3多重共线性

数据预处理
对数据进行清洗，处理缺失值和异常 值，进行描述性统计分析和可视化， 以初步了解数据分布和特征。
模型构建与求解过程
变量选择
模型设定
模型求解
根据研究目的和理论基础，选 择与被解释变量（贷款违约风 险）相关的解释变量（如年龄 、收入、负债比等），并控制 其他可能影响结果的变量（如 性别、教育程度等）。
诊断工具
相关系数矩阵
通过观察解释变量之间的相关系数，可以初步判断是否存在多重 共线性。当相关系数较高时，可能存在多重共线性问题。
散点图与回归分析
通过绘制散点图并进行回归分析，可以直观地观察解释变量之间的 线性关系，从而判断是否存在多重共线性。
方差分解与主成分分析
利用方差分解和主成分分析方法，可以诊断多重共线性的来源和影 响程度。
采用多元线性回归模型，以贷 款违约风险为被解释变量，以 上述解释变量为自变量，构建 计量经济学模型。
运用最小二乘法（OLS）对模型 进行求解，得到各解释变量的系 数估计值、标准误、t统计量和p 值等。
结果展示与解读
结果展示
将模型求解结果以表格形式展示，包括各解释变量的系数估计值、标准误、t统计量、p值和置信区间等。
检验方法
方差膨胀因子（VIF）检验
通过计算解释变量的方差膨胀因子，判断是否存在多重共线性。当VIF值远大于1时，表明存在严 重的多重共线性。
条件指数（CI）检验
利用条件指数的大小来判断多重共线性的程度。条件指数越大，多重共线性问题越严重。
特征根与条件数检验
通过计算特征根和条件数来判断多重共线性的存在。当特征根接近于0或条件数较大时，表明存 在多重共线性。
案例分析
案例一
通过收集某地区房价、人口、收入等变量的数据，建立计量经济学模型进行实证分析。在模型检验过 程中，发现房价与人口、收入之间存在较高的相关系数，且VIF值较大，表明存在多重共线性问题。 经过进一步诊断和处理，最终得到合理的模型结果。

计量经济学 第七章 多重共线性

第七章 多重共线性“多重共线性”一词由R. Frisch 1934年提出，它原指模型的解释变量间存在线性关系。

7.1多重共线性及产生的原因 7.1.1．非多重共线性假定111211212221121111k k T T Tk x x xx xx X x x x ---=如果rk (X 'X ) = rk (X ) ＜ k 或`0X X =称解释变量是完全共线性相关。

在实际经济问题中，完全多重共线性和完全无多重共线性两种极端情况都是极少的，大多数情况是解释变量存在不完全的多重共线性，或者近似的多重共线性，可一表示为：1122110k k x x x u λλλ--++++= 7.1.2．多重共线性的经济解释（1）经济变量在时间上有共同变化的趋势。

如在经济上升时期，收入、消费、就业率等都增长，当经济收缩期，收入、消费、就业率等又都下降。

当这些变量同时进入模型后就会带来多重共线性问题。

0.E+001.E+112.E+113.E+114.E+11808284868890929496980002GDPCONS0.E +001.E +112.E +113.E +114.E +110.0E +005.0E +101.0E +111.5E +112.0E +112.5E +11C O N SG D P o f H o n g K o n g（2）解释变量与其滞后变量同作解释变量。

滞后变量与原因变量在经济意义上没有本质区别，只是时间上的差异，原因变量与解释变量有相关关系，滞后变量也会有相关关系。

（见下图） （3）解释变量之间往往存在密切的关联度。

对同一经济现象的解释变量，往往存在密切的相关关系，如生产函数，资本大，需投入的劳动力也应趆多。

0.E+001.E+112.E+113.E+114.E+11GDP0.E+001.E+112.E+113.E+114.E+110.E+001.E+112.E+113.E+114.E+11GDP(-1)GDP7.2．多重共线性的后果（1） 当 `0X X =，X 为降秩矩阵，则 (X 'X ) -1不存在，βˆ= (X 'X )-1 X 'Y 不可计算。

计量经济学多重共线性的分析


检验多重共线性
➢ 检验简单相关系数
进一步选择Covariance Analysis的Correlation，得到变 量之间的偏相关系数矩阵，观察偏相关系数。
可以发现，Y与X1、X2、X3的相关系数都在0.9以上 ，但输出结果中，解释变量X1、X3的回归系数却无 法通过显著性检验。认为解释变量之间存在多重共 线性。
➢ 收集整理实验数据 ➢ 建立线性回归模型 ➢ 检验多重共线性 ➢ 用逐步回归法克服多重共线性
收集整理实验数据
1978年至2011年我国税收收入与国民生产总值情况
（来源于中国统计年鉴）
建立线性回归模型
➢ 用普通最小二乘法估计模型
利用实验数据分别建立Y关于X1、X2、X3的散点图 （SCAT Xi Y）
建立线性回归模型
➢ 用普通最小二乘法估计模型
利用实验数据分别建立Y关于X1、X2、X3的散点图 （SCAT Xi Y）
根据散点图可以看出Ｙ与 X1、X2、X3都呈现正 的线性相关，
建立线性回归模型
➢ 建立一个多元线性回归模型
输出结果，只有X2的系数通过显著性检验， 其他没有通过，而Ｆ值很大，通过了显著性 检验，判断模型存在多重共线性。
用逐步回归法克服多重共线性
➢ 找出最简单的回归形式
Y=24023.76+4.1804X1 (5.887) (36.5072) R2=0.977979
D.W.=0.1937
Y=-1592.676+2.6322X2 (-1.1194) (116.4316) R2=0.997792 D.W.=0.6285
用逐步回归法克服多重共线性
➢ 逐步回归
第一步，引入变量X1
用逐步回归法克服多重共线性

计量经济学实验报告 多重共线性检验

计量经济学上机实验报告多重共线性检验实验背景近年来，中国旅游业一直保持高速发展，旅游业作为国民经济新的增长点，在整个社会经济发展中的作用日益显现。

中国的旅游业分为国内旅游和入境旅游两大市场，入境旅游外汇收入年均增长22.6%，与此同时国内旅游也迅速增长。

改革开放20多年来，特别是进入90年代后，中国的国内旅游收入年均增长14.4%，远高于同期GDP 9.76%的增长率。

为了规划中国未来旅游产业的发展，需要定量地分析影响中国旅游市场发展的主要因素。

模型•其中，•Yt——第t年全国旅游收入•X2——国内旅游人数（万人）•X3——城镇居民人均旅游支出（元）•X4——农村居民人均旅游支出（元）•X5——公路里程（万公里）•X6——铁路里程（万公里）Y = 0.0639689468*X2 + 0.2098186372*X3 + 5.283346538*X4 - 3.352906602*X5 - 53.38584085*X6 - 2220.150544数据来源中国统计局网站样本区间1994——2009实验过程及结果（一）实证结果Dependent Variable: YMethod: Least SquaresDate: 04/06/11 Time: 15:49Sample: 1994 2009Included observations: 16Variable Coefficient Std. Error t-Statistic Prob.X2 0.063969 0.007714 8.292875 0.0000X3 0.209819 1.319292 0.159039 0.8768X4 5.283347 1.918838 2.753409 0.0204X5 -3.352907 2.376484 -1.410869 0.1886X6 -53.38584 434.6829 -0.122816 0.9047C -2220.151 2210.044 -1.004573 0.3388R-squared 0.994274 Mean dependent var 4270.119Adjusted R-squared 0.991411 S.D. dependent var 2720.860S.E. of regression 252.1678 Akaike info criterion 14.17806Sum squared resid 635886.0 Schwarz criterion 14.46778Log likelihood -107.4245 F-statistic 347.2644Durbin-Watson stat 1.224560 Prob(F-statistic) 0.000000R2很高，F显著，但x3、x5、x6不显著，X5、X6的符号甚至是负的。

计量经济学试题计量经济学中的多重共线性问题与解决方法

计量经济学试题计量经济学中的多重共线性问题与解决方法计量经济学试题-多重共线性问题与解决方法在计量经济学中，多重共线性是一个重要的问题。

它指的是当两个或多个自变量之间存在高度相关性时，会导致模型估计的结果不准确或者不可靠。

多重共线性问题在经济学研究中经常出现，因此探索解决方法是非常必要的。

一、多重共线性问题的原因多重共线性问题通常由于样本中的自变量之间存在强烈的线性相关性而引发。

例如，当一个自变量可以通过其他自变量的线性组合来表示时，就会出现多重共线性问题。

这种情况下，模型估计的结果会变得不稳定，标准误差会变得很大，使得对自变量的解释变得困难。

二、多重共线性问题的影响多重共线性问题对计量经济模型的影响是多方面的。

首先，它会导致模型估计结果的不稳定性。

当自变量之间存在高度相关性时，即使是微小的样本误差也会导致模型估计结果的显著变化。

其次，多重共线性问题会导致标准误差的上升，使得参数的显著性检验变得困难。

最后，多重共线性问题还会导致模型解释力的下降，使得对自变量对因变量的影响进行准确的解释变得困难。

三、解决多重共线性问题的方法1. 删除变量：当发现自变量之间存在高度相关性时，一种解决方法是删除其中一个变量。

如果某个自变量可以用其他变量线性表示，就可以考虑将其删除。

然而，删除变量的过程需要谨慎，以免造成结果的失真。

2. 采用主成分分析：主成分分析是一种常用的处理多重共线性问题的方法。

它通过对自变量进行线性组合，生成新的主成分变量，从而消除原始自变量之间的相关性。

通过采用主成分分析，可以得到一组无关的自变量，从而解决多重共线性问题。

3. 利用岭回归：岭回归是一种通过增加正则化项来减小模型参数估计标准误差的方法。

通过岭回归，可以有效地解决多重共线性问题。

岭回归对相关自变量的系数进行惩罚，从而减小系数估计的方差。

这种方法可以提高模型的准确性和稳定性。

4. 使用其他估计方法：在实际应用中，还可以采用其他估计方法来解决多重共线性问题。

多重共线性(Multi-Collinearity)


i 0 1 1i 2 2i
k ki i
（i=1,2,…,n）
其基本假设之一是解释变量
X,
1
X2,,
X
k
互相独立 。
如果某两个或多个解释变量之间出现了相关性， 则称为多重共线性。
如果存在
c1X1i+c2X2i+…+ckXki=0
i=1,2,…,n
其中: ci不全为0，即某一个解释变量可以用其它解释 变量的线性组合表示，则称为解释变量间存在完全
2

1

x12i 1 r 2
2
x12i
所以，多重共线性使参数估计量的方差增大。
方差扩大因子(Variance Inflation Factor)为1/(1-r2)， 其增大趋势见下表：
相关系 0 0.5 0.8 0.9 0.95 0.96 0.97 0.98 0.99 0.999 数平方 方差扩 1 2 5 10 20 25 33 50 100 1000 大因子
多重共线性(Multi-Collinearity)
§2.8 多重共线性
Multi-Collinearity
一、多重共线性的概念 二、多重共线性的后果 三、多重共线性的检验 四、克服多重共线性的方法 五、案例
一、多重共线性的概念
1、多重共线性
• 对于模型
Y X X X
以二元回归模型中的参数估计量ˆ 为例，ˆ 的方差为
1
1
Var(ˆ )
1

ˆ 2

(X X
)1
22

(
ˆ
2
(
x2
2i
)
x2 )( x2 ) ( x
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

4、解释变量X（j j 1，2， ，k）是确定性变量, 不是随机变量,
与随机扰动项ui不相关，即Cov（X ji，u）i 0
5、
无多重共线性。
即解释变量X
，X
1
2，
，X
之间不存在
k
线性关系。
6、u服从正态分布，ui ~ N（0， 2）
2020/5/8
重庆工商大学经济贸易学院 张文爱
3/21
如果假设5不成立，即在解释变量X1，X2，…，Xk间，存 在线性关系，则此时模型就出现了多重共线性。
9/21
5、判定系数检验法
利用解释变量之间的拟合优度（判定系数）检验模 型的多重共线性。
①每次以一个解释变量对余下的k-1个解释变量做回归，
即建立k个回归方程，回归得到判定系数R
2 j
：
X1
g（1 X
2，X 3，
，X
）
k
R12
X2
g（ 2 X1，X 3，
，X
）
k
R
2 2
Xk
g（ k X1，X
2，
（其中vi 为随机项。）
同样假定λ1 ≠0，
X 1i
0 1
2 1
X 2i
3 1
X 3i
k 1
X
ki
vi
1
此时称模型具有近似的多重共线性。
2020/5/8
重庆工商大学经济贸易学院 张文爱
6/21
§7-2 多重共线性的来源与后果
一、多重共线性的来源
1、计量经济学研究依据的两个原则：
（1）相关性原则； （2）连贯性原则
多重共线性（或“不完全多重共线性”）。
2020/5/8
重庆工商大学经济贸易学院 张文爱
4/21
（1）完全的多重共线性。 解释变量间存在完全(确定)的线系关系，即存在
不全为零的常数 0 , 1, 2 , k，使
0 1 X1i 2 X 2i k X ki 0
不妨设1 0, 则
X 1i
0 1
多重共线性的概念：
在多元线性回归模型: Yi 0 1X1i 21X 2i k X ki i
（i=1,2,……，n）中,如果解释变量X1，X2，…，Xk之间存在 线性关系，则称模型存在多重共线性。
其中： 解释变量之间存在完全的线性关系，称称模型存在完全的
多重共线性； 解释变量之间存在近似的线性关系，称称模型存在近似的
多重共线性并没有违背最小二乘参数估计的古典假设，因此， 在存在近似的多重共线性的情况下，只要模型不违背CLRM的 古典假设，则OLS估计量就具有线性、无偏性和最小方差性。
2020/5/8
重庆工商大学经济贸易学院 张文爱
8/21Βιβλιοθήκη §7-3 多重共线性的检验
1、相关系数法
（1）两个解释变量模型：相关系数法 （2）多个解释变量模型：偏相关系数法
2、多重共线性的来源
（1）经济变量在时间上有共同变化的趋势 （相关性原则）； （2）模型中引入滞后解释变量引起多重共线性 （连贯性原则）
由于经济变量自身的性质，多重共线性或强或弱，是普遍存在的。
2020/5/8
重庆工商大学经济贸易学院 张文爱
7/21
二、多重共线性的后果
1、对于完全的多重共线性，参数的最小二乘估计量是 不确定的，其方差为无穷大。
2、对于近似多重共线性，参数的最小二乘估计量是确 定的，而且是无偏的，但方差较大，有以下后果：
（ 1）参数估计值不精确，也不稳定，对观测值的轻微变化较敏感， 参数估计量的符号可能错误。
（2）参数估计值的标准差较大，使参数的显著性 t 检验值变小， 增大了接受H0的可能，从而舍弃对因变量有显著影响的变量。
2/21
其基本假定为：
1、 零均值。 指随机误差项是一个期望值为零的随机变量，
即E（ i） 0 （i 1，2， ，n）
2、 同方差。 指随机误差项的方差相同， 即Var(i ) 2
3、u无自相关，即Cov（ui，u ）j E{[ui Eui ][u j Euj ]}
E（uiu ）j 0 i j
2、参数估计值的经济意义检验 3、参数估计值的稳定性检验 4、参数估计值的统计检验
根据R2、F、t检验结果进行综合分析检验: 无多重共线性： R2、F、t检验均显著 存在多重共线性： R2、F检验很显著，但t检验不全显著
（一般是不显著的X与显著的X存在共线性。）
5、判定系数检验法
2020/5/8
重庆工商大学经济贸易学院 张文爱
可以提高参数估计的精度。
2020/5/8
重庆工商大学经济贸易学院 张文爱
重庆工商大学经济贸易学院 张文爱
11/21
1、增加样本容量
如果多重共线性是由样本引起，增加样本容量可以减少多 重共线性的程度。以二元回归方程为例，根据第二节的结果，参 数估计值的方差为：
Var(ˆ1)
xi21
2
xi21
xi22 （
xi1
xi
）2
2
2
xi22
(1
r2 12
)
当样本容量增大时， xi21 增大，方差将减小，
，X
k
）
1
R
2 k
②记R 2 Max（R12，R22， ，Rk2）
若R 2
R
2 j
1，则认为X
与其余变量之间
j
存在较严重的线性关系, 模型具有多重共线性;
否则，则没有多重共线性。
2020/5/8
重庆工商大学经济贸易学院 张文爱
10/21
§7-4 多重共线性的修正
i ：如果多重共线性对参数的估计值没有严重影响，可以不修正；
第7章 多重共线性
（Multicollinearity）
授课教师 张文爱 重庆工商大学 ·经济贸易学院
2010. 12
§7-1 多重共线性的概念
回顾：多元线性回归模型
Yi 0 1X1i 21X 2i k X ki i
（i=1,2,……，n）
2020/5/8
重庆工商大学经济贸易学院 张文爱
2 1
X 2i
3 1
X 3i
k 1
X ki
此时称模型具有完全的多重共线性。
2020/5/8
重庆工商大学经济贸易学院 张文爱
5/21
（2）近似的多重共线性 解释变量间存在不完全的线性关系，即存在不
全为零的数：0 , 1, 2 , k，使
0 1 X1i 2 X 2i k X ki 0
或者：0 1 X1i 2 X 2i k X ki vi 0
ii ：如果多重共线性只影响到某些不重要的解释变量对应的参数 估计值，可以在模型中删去这些解释变量；
iii ：如果多重共线性对重要的解释变量对应的估计值有严重影响， 就必须消除这种多重共线性的影响，保证模型的正确性和估计的 有效性。
修正的基本思想：
不是改变参数的估计方法，而是修改模型本身。
2020/5/8