当前位置：文档之家 › 条件平差

条件平差

  • 格式：ppt
  • 大小：2.29 MB
  • 文档页数：81

下载文档原格式

  / 81

合集下载

条件平差公式

条件平差公式

条件平差公式
条件平差公式是一种用于对多个测量值进行分析和校正的数学方法。

其基本原理是，将所有测量值组成一个方程组，其中每个方程表示一个测量量与其他测量量之间的关系。

通过求解这个方程组，可以得到每个测量值的最优估计值和方差。

具体地说，条件平差公式可以分为两类：一类是基于观测方程的条件平差公式，另一类是基于误差方程的条件平差公式。

观测方程的条件平差公式是指，将所有测量值表示为观测方程的形式，然后通过最小二乘法求解得到最优估计值和方差。

观测方程通常表示为线性方程组的形式，即y=AX+e，其中y表示观测值，A表示系数矩阵，X表示未知数向量，e表示误差向量。

误差方程的条件平差公式是指，将所有误差表示为误差方程的形式，然后通过最小二乘法求解得到最优估计值和方差。

误差方程通常表示为非线性方程组的形式，即f(X)=e，其中f表示误差函数，X表示未知数向量，e表示误差向量。

无论是基于观测方程还是基于误差方程的条件平差公式，都具有很强的实用性和广泛的应用范围。

它们可以用于地理测量、航空测量、工程测量等领域，对于提高测量精度和减小误差具有重要意义。

- 1 -。

条件平差原理

条件平差原理

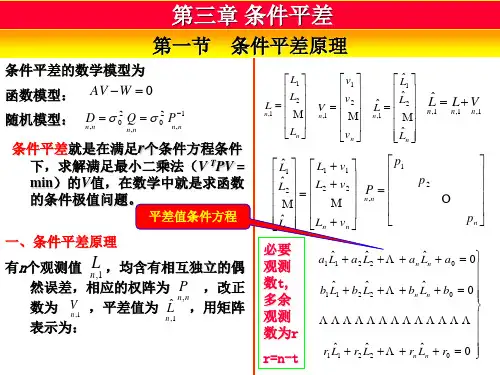
§9.1 条件平差原理在条件观测平差中，以n 个观测值的平差值1ˆ⨯n L 作为未知数，列出v 个未知数的条件式，在min =PV V T 情况下，用条件极值的方法求出一组v 值，进而求出平差值。

9.1.1基础方程和它的解设某平差问题，有n 个带有相互独立的正态随机误差的观测值 ，其相应的权阵为 ， 它是对角阵，改正数为 ，平差值为 。

当有r 个多余观测时，则平差值 应满足r 个平差值条件方程为：⎪⎪⎭⎪⎪⎬⎫=++++=++++=++++0ˆˆˆ0ˆˆˆ0ˆˆˆ221122112211οοοr L r L r L r b L b L b L b a L a L a L a n n n n n n （9-1） 式中i a 、i b 、…i r （i =1、2、…n ）——为条件方程的系数；0a 、0b 、…0r ——为条件方程的常项数以ii i v L L +=ˆ（i =1、2、…n ）代入(9-1)得条件方程（9-2）式中a w 、b w 、……r w 为条件方程的闭合差，或称为条件方程的不符值，即（9-3） 令⎪⎪⎪⎪⎪⎭⎫⎝⎛=⨯n n n n r r r r b b b a a a A212121⎪⎪⎭⎪⎪⎬⎫++⋅⋅⋅++=++⋅⋅⋅++=++++=022110221102211r L r L r L r w b L b L b L b w a L a L a L a w n n n n n b n n a ⎪⎪⎭⎪⎪⎬⎫=++⋅⋅⋅++=++⋅⋅⋅++=++⋅⋅⋅++000221122112211r n n b n n a n n w v r v r v r w v b v b v b w v a v a v a ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⨯n n L L L L 211⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⨯n n L L L L ˆˆˆˆ2111⨯n L nn P ⨯1⨯n V 1ˆ⨯n L 1ˆ⨯n L则(9-1)及（9-2）上两式的矩阵表达式为0ˆ0=+A LA （9-4） 0=+W AV （9-5）上改正数条件方程式中V 的解不是唯一的解，根据最小二乘原理，在V 的无穷多组解中，取PV V T = 最小的一组解是唯一的，V 的这一组解，可用拉格朗日乘数法解出。

条件平差与间接平差的相互关系

条件平差与间接平差的相互关系

条件平差与间接平差的相互关系
一、条件平差与间接平差
1、条件平差与间接平差是指：条件平差是指基础数据是现有被观
测坐标信息，假定各点位置坐标值满足一定近似关系时（即解算中假
定有约束关系或条件，以达到所求结果的平差方法）；而间接平差是指，基础数据是待测点的被观测量，包括方位量、距离量等，无任何
关系的前提条件，是一种完全无条件的平差方法。

二、条件平差
2、条件平差一般会把条件设置为两个系统中坐标值的差值最小，
这样就能够更容易地实现平差。

条件平差的典型应用是重叠法平差，
它会利用各观测值之间的内在联系，并通过设定一定的几何条件，使
其之间被观测量满足某一关系，以解决无条件方程组的平差问题。

三、间接平差
3、间接平差是指以被观测量构成的方程组，可以以各种迭代方法
求解，但是必须有一定的条件限制才能使解出的坐标值符合实际要求。

加拿大匹兹堡大学的Bloch教授认为，从下面几个原因考虑起，最好
用间接平差来解决坐标转换的问题：
（1）传统的解算序号很容易引起原点偏移和比例错误；
（2）间接平差可以很好地表示待解系统中的不确定性；
（3）使用间接平差可以很好地降低待解系统中分量精度和消隐关
系统时发生的偏差。

四、条件平差与间接平差的关系
4、条件平差与间接平差是有联系的，相互之间的联系是：可以把
条件平差看做是一种特殊的间接平差，即在无条件间接平差的基础上，再加入解算中的限制条件，以达到所求结果。

可以说，条件平差是间
接平差的分支，而间接平差是条件平差的总集合。

第三章条件平差

第三章条件平差

独立三角网
自由三角网
自由测角网
附合三角网（测角）
• 例：
∆ቤተ መጻሕፍቲ ባይዱ
α ∆
当n=35、n=22、n=35+22时，其条件式个数各为多 少？有哪些类型？
图形条件（内角和条件）:
B
b1
a2
c1 D c2 a1 b3 c3 a3 b2 C
A
圆周条件（水平条件）:
b1
a2
c1 a1 a3 c3
c2 b2 b3
5.1.06、 5.1.07
上节内容回顾：
改正数条件式 观测值的协方差阵 法方程
AV W 0
D P Q
2 0 1 2 0
r n n n
Naa K W 0 N aa AQ AT
r r n r
改正数方程
V P A K QA K
T
1 T
wr
T
• 则条件方程可写成：
ˆA 0 AL 0
• 以及改正数条件式：
W AL A0
AV W 0
这样一来，对于一个平差问题，我们能够得到 其数学模型：
AV W 0 D P Q
2 0 1 2 0
下面要解决的问题是： 由上述的数学模型来求改正数V。
不难发现，不能求得V的唯一解！！！ 解决不唯一解的办法就是附加一个约束条件---“最小二乘估计” 即满足：
极条件（边长条件）:
b1 a2
c1
a1 b3 c3
c2 b2 a3
极条件（边长条件）就是指由不同路线推算得到 的同一边长的长度应相等。
三角网的基本图形 1） 单三角形 2）大地四边形
3）中点多边形。

第五章条件平差

第五章条件平差

二、法方程及改正数方程
将V T PV min的原则作用于条件方程 。
组成新函数:
V T PV－2k T AV W
式中
r 1
k k a , kb , k r 条件方程联系数
T
对新函数求导： T T 2V P 2A k ---改正数方程
dSCD ˆ f T dL SCD ˆ SCD T 2 T ˆ f D f f QL ˆL ˆ ˆL ˆ f 0 L S CD
得测边相对中误差为： 3、大地四边形测角网
2
ˆS
CD
SCD
＝
ˆ 0 f T QL ˆL ˆ f
设
F ( f1 , f 2 , f m )
T T
G ( g1 , g 2 , g m ) 有
均为m维向量函数，且 f i、g i 均为x的函数， d F G dG F T dG T dF F G dx dx dx dx
注意：当N为满秩方阵时，才有 N 1唯一存在,法方程才有唯
测方向网
测角网
测角网
三角网
测边网
测边长
测边＋测方向
边角网
（导线网） 测边＋测角
三、三角网的布设－－从高级到低级逐级布设 四、三角网平差的方法 1。严密平差 ----遵守VTPV=min原则 ； 2。近似平差
5.3 测角网条件平差
独立网（经典自由网）－-－只有必要起算数据d。
非独立网（附合网）－-－已知条件超过必要起算数据。
3 图形条件： n=12 t=2×2+4=8 r =4 1 极条件：
v2 v1 v6 v5 v11 v10 W1 0

测量程序设计_条件平差和间接平差

测量程序设计_条件平差和间接平差

程序代码如下：
disp(‘-------水准网间接平差示例-------------’) disp(‘已知高程’) Ha = 5.015 % 已知点高程，单位m Hb = 6.016 % 已知点高程，单位m
A h2 D h1
C h6 E h7 B h4
h5
h3
disp(‘观测高差，单位m’)
L = [1.359; 2.009; 0.363; 1.012; 0.657; -0.357] disp(‘系数矩阵B’)
则： PV AT K
V P A K QA K
T
1 T
4、法方程： 将条件方程 AV+W=0代入到改正数方程V=QATK 中，则得到：
AQAT K W 0
r1 r1 r1
记作： 由于
N aa K W 0
rr
R( Naa ) R( AQAT ) R( A) r
Naa为满秩方阵， K Naa1W ( AQAT )1 ( AL A0 )
if H(1,1)+H(2,1)-H(3,1)+HA-HB==0 && H(2,1)H(4,1)==0 disp(‘检核正确') else disp(‘检核错误') end disp(‘平差后的高程值') HC = HA + H(1,1) HD = HA + H(1,1) + H(4,1)
二、间接平差的基本原理
其中l＝L－d.
ˆ 设误差Δ和参数X的估计值分别为V 和 X
则有
ˆ V AX l
X0 为了便于计算，通常给参数估计一个充分接近的近似值
ˆ ˆ X X0 x
则误差方程表示为

误差理论与测量平差基础第五章条件平差ppt课件.pptx

误差理论与测量平差基础第五章条件平差ppt课件.pptx

5-2 条件方程的列立
故有：
dA
1 ha
(dSa
cos CdS b
cos BdSc
)
将微分换成改正数，并将弧度换
成角度，得：
vA
ha (vSa
cos CvSb
cos BvSc
)
上式称为角度改正数方程。它具有明显的规律：
任意角度的改正数，等于其对边的改正数分别减去两邻 边的改正数乘以其邻角的余弦，然后再除以该角至其对边的
3、几种非线性条件方程的线性形式
极条件： 在图5-4中，极条件为 线性化得：
sin aˆ1 sin aˆ2 sin aˆ3 sin bˆ1 sin bˆ2 sinbˆ3
1
sin(a1 va1 )sin(a2 sin(b1 vb1 )sin(b2
va2 )sin(a3 va3 ) vb2 )sin(b3 vb3 )
dV
dV
dV
VTP VTP
2V T P
5-1 条件平差原理
2.2 求偏导
2.3 法方程 改正数方程
d 2V T P 2K T A 0 dV
AP1 AT K W 0
V P1 AT K
举例
水准网如右图：观测值及其权阵如下：
L 0.023 1.114 1.142 0.078 0.099 1.216 T m
m1
yA yˆi yB 0 i 1
5-2 条件方程的列立
➢GIS数字化数据采集中，折角均为90度的N边形的条件 方程
1、观测值
观测值为N个顶点的坐标，其个数为n=2 N。
2、必要观测个数
t=N+1
h
3、多余观测个数
r=n-t=2N-N-1=N-1 4、条件方程的类型

第三章 条件平差

第三章 条件平差
纵横坐标附合条件：从起始点推算至终点所得到的坐标 平差值应与终点的已知坐标值相等，即
xˆn1 xC 0 yˆ n1 yC 0
单一附合导线条件平差
1.方位角附合条件式
Tˆn1 T0 [ˆi ]1n1 (n 1) 180 T0 [i vi ]1n1 (n 1) 180
则方位角附合条件式可写为
v2
Lˆ n
Ln
vn
在这n个观测值中，有t个必要观测数，多余观测
数为r。
条件平差原理
可以列出r个平差值线性条件方程
a1v1 a2v2 an vn wa 0
b1v1
b2v2 bn vn wb 0
r1v1 r2v2 rn vn wr 0
程中式的式中常中，数的ai、项系b。i数、相，…应、a0的、ri（改b0i、正= …1数,2、条,…r件0…为方n各）程平为式差各值平条差件值方条程件方式
E QAT
0
N 1 QAT N 1
0
N 1 AQ QAT N 1 AQ
0
0
0
Q
QAT
N
1
AQ
QLˆL
QLˆW
QLˆK
QLˆV
QLˆLˆ
由上式可见，平差值与闭合差W、联系数K、改 正数V是不相关的统计量，又由于它们都是服 从正态分布的向量，所以与W、K、V也是相互 独立的向量。
平差值函数的协因数
单一附合导线条件平差
设AB边方位角已知值为TAB = T0，CD边方位角已知值为TCD、 计算值为Tn+1，B点坐标的已知值为(,)或者(x1, y1)，C点坐 标的已知值为(,)、计算值为(xn+1, yn+1)。三个条件中，有 一个方位角附合条件、两个坐标附合条件。

条件平差算例

条件平差算例

一、水准网条件平差示例 范例：有一水准网（如图8-3所示），已知点A ，B 的高程为: HA=50.000m ， HB=40.000 m ，观测高差及路线长度见表8-1。

试用条件平差求:(1) 各观测高差的平差值；(2) 平差后P 1到P 2点间高差的中误差。

图8-3【解】1）、求条件方程个数；由图易知：n=7，t=3，条件式r=4。

故应列4个平差值条件方程，三个闭合环，一个附和路线2）、列平差值条件方程； 所列4个平差值条件方程为：⎪⎪⎭⎪⎪⎬⎫=-+-=--=-+=+-0ˆˆ0ˆˆˆ0ˆˆˆ0ˆˆˆ31643765521BA H H h h h h h h h h h h h 3)、转换成改正数条件方程；以ii i V L L +=ˆ代入上式可得： ⎪⎪⎭⎪⎪⎬⎫=-+-+-=--+--=-++-+=+-++-00003131643643765765521521B A H H h h v v h h h v v v h h h v v v h h h v v v 化简可得：⎪⎪⎭⎪⎪⎬⎫=--=+--=+-+=++-0403070731643765521mm mm mm mm v v v v v v v v v v v 可知条件方程系数阵为：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----000101010110011100000010011⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=2101001000210000210000010000001称对P ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=2010010002000020000010000001称对Q ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----=320125100141101300100110001101001100000110010002010102200211000000100114)、组成法方程； 先求权阵P ；以1km 观测高差为单位权观测高差，则： 11=P ，12=P ，213=P ，214=P ，15=P ，16=P ，217=P ，而各观测高差两两相互独立，所以权阵为：，则协因数阵为：则，法方程的系数阵Naa 为：⎥⎥⎦⎤⎢⎢⎣⎡-----⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----==-=00010101011001110000001001120100100020000200000100000010001010101100111000000100111TT AQA T A AP aa N 称对所以，法方程为：043773212510014110134321=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----k k k k 5）、解算法方程，求出联系数K⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡34831.213483.002247.177528.2437758427.025843.012360.023596.025843.032584.011236.012360.012360.011236.031461.014607.023596.012360.014608.046067.04377320125100141101314321k k k k 6）、求V 及高差平差值Lˆ 所以4210.212.118.3213.0214.418.214.0ˆ22222220⨯+⨯-+⨯-+⨯-+⨯-+⨯+⨯-==）（）（）（）（）（r PV V T σ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-----=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-------⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡==045.2157.1798.3270.0427.4775.2427.034831.213483.002247.177528.2002001100011020022000001100134831.213483.002247.177528.200001010101100111000000100112010010002000020000010000001m m T K T QA V 称对mmmm v v v v v v v h h h h h h h h h h h h h h L ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----+⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=5020.108548.56472.45007.143556.200028.153556.100.22.18.33.04.48.24.0500.10856.5651.4501.14360.20000.15356.10ˆˆˆˆˆˆˆˆ7654321765432176543217）、精度评定1）、单位权方差估值计算mm 98.24605.35±==2）、建立所求精度的平差值函数的算式，并按误差传播律求平差值函数的精度 依题意列平差值函数为： 5ˆh =ϕ 则:[]Tf 0010000=[][][][]51687.048313.01)16853.3146.0(1001111236.001124.016853.03146.0100110011111ˆˆ=-=+-=⨯---=-=-=--TTT T T aaaa N AQf N QA f Qf fQ ϕϕ所以：mm Q 14.251687.098.2ˆˆ0ˆ±=⨯==ϕϕϕσσ【答】：各观测高差的平差值为：}{m m m m m m m5020.108548.56472.45007.143556.200028.153556.10平差后P1到P2点间高差的中误差为：±2.14mm987654321ACPB 图8-11二、测角网条件平差 范例：有一测角网（如图8-11所示），A 、B 、C 三点为已知三角点，P 为待定点。

3.1第1讲(条件平差原理)

3.1第1讲(条件平差原理)
平差值条件方程
v1 v 2 V = n ,1 M v n
ˆ L1 ˆ L ˆ L = 2 n ,1 M ˆ Ln
n ,1
ˆ L = L+V
n ,1
n ,1
p1 ˆ L1 L1 + v1 ˆ L2 + v 2 P = L2 = M M n ,n ˆ Ln + v n Ln
p2
O pn
一、条件平差原理
L 有n个观测值 n ,1 ，均含有相互独立的偶
然误差， 然误差，相应的权阵为 P ，改正 n,n ˆ V ，平差值为 L ，用矩阵 数为 n,1 n ,1 表示为： 表示为：
2012-3-29
必要 观测 数t, 多余 观测 数为r 数为r r=nr=n-t
1
第三章 条件平差
第一节
改正数条件方程： 改正数条件方程： a1v1 + a 2 v 2 + L + a n v n − wa = 0 b1v1 + b2 v 2 + L + bn v n − wb = 0 LLLLLLLLLLLLL r1v1 + r2 v 2 + L + rn v n − wr = 0 方程的闭合差
ˆ 2. L、W、K、V、L 的协因数阵及互 协因数阵
L=L
W = −( AL + A0 ) = − AL − A0
K = N −1W = − N −1 ( AL + A0 ) = − N −1 AL − N −1 A0 V = P −1 AT K
传播律中的K 传播律中的K

6 第五章 条件平差

6 第五章 条件平差

三角网的基本图形构成
单三角形； 大地四边形； 中点多边形
30
§2 条件方程
二.三角网 1.独立测角网条件方程
测角网的观测值
测角网的观测值很简单,全部是角度观测值
测角网的作用
确定待定点的平面坐标
测角网的基准
位置基准2个(任意一点坐标X0Y0) 方位基准1个(任意一边方位角α0) 长度基准1个(任意一边的边长S0)
Av f 0
V PV min
T
在满足 Av f 0 的条件下，
求函数 V PV min 的V值
T
条件 极值 问题
4
§1 条件平差原理 条件平差的步骤
5
§1 条件平差原理
列条件方程 观测值权阵
最小二乘原则
求唯一解
6
§1 条件平差原理 一.基础方程及其解
r个线性条件方程：
3 ka 3 k 2 0 6 b
写成矩阵形式：
(2)定权： 100米量距为单位权：Pi=100/Si
1/Pi=Si/100 1/P1=2， 3=3， 1/P 1/P2=3， 4=5， 1/P
2 0 Q 0 0 0 3 0 0 0 0 3 0 0 0 0 5
AV f 0 PLL diag p1 p2 p4
组、解法方程： AQAT K f 0
由改正数方程求： V P A K
T 1
ˆ 求平差值： L L V
15
§1 条件平差原理 二.条件平差的求解步骤及示例
条件平差计算步骤
16
§1 条件平差原理
例：
r 1
r 1
r个改正数条件式：
a1v1 a2 v2 an vn wa 0 b1v1 b2 v2 bn vn wb 0 r1v1 r2 v2 rn vn wr 0

第三章 条件平差

第三章 条件平差

返回目录 返回本节
经化简即有
cv t c g v ta c gv t a c g v t a c g v t b c g v tb g b
1 a 1
2 a 2
3 a 3
1 b 1
2 b 1
33
(1
sina1 sinb1
sina2 sinb2
sina3)
sinb3
=0,
圆周条件，即
c ˆ1c ˆ2c ˆ336 o0
或
V V V W 0
c1
c2
c3
4
第三类是极条件或称边长条件。满足上述4个条件方程
的角值还不能使图3-5的几何图形完全闭合，例如，由边
长通过a2、b2、c2计算边长，通过a1、b1、c1由计算边长，
再由通过a3、b3、c3计算边长，计算的结果，其边长不会
(3-21)
这就是极条件（3-20）的线性形式。
三、测边网
和测角同一样，在测边网中也可分解为三角形，大地 四边形和中点多边形三种基本图形。对于测边三角形，决 定其形状和大小的必要观测为三条边长。所以t=3，此时 r=n-t=3-3=0，即测边三角形不存在的条件方程。对于测边 四边形，决定第一个三角形必须观测3条边长，决定第二 个三角形只需要再增加2条边长，所以确定一个四边形的 图形，必须观测5条边长，即t=5，所以r=n-t=6-5=1，存在 一个条件方程。对于中点多边形，例如中点五边形，它由 四个独立三角形组成，此t=3+2×3=9，故有r=n-t=10-9=1。
法，将上式用台劳公式展开取至次项，即可得线性形式的
极条件方程。
将 a ˆ a v,b ˆ b v,c ˆ c v代入（3-20）式，

第五章 条件平差

第五章 条件平差
ˆ 0 F L
v1 v V 2 n ,1 vn
W AL A0
则相应方程的矩阵表达式分别为

AV W 0
第五章：条件平差
3. 基础方程
按求函数极值的拉格朗日乘数法，设乘数 联系数向量。组成函数 将 φ 对V 求一阶导数，并令其为零，得

r , n n ,1
A V W 0 ——改正数条件方程 r ,1
W AL A0 —改正数条件方程常数项（闭合差）计算式
第五章：条件平差
例题 ：右图中L1、L2、L3为观测角度， 试列出该图形的条件方程和改正数条件方 程。 解：t=2, r=n-t=3-2=1 条件方程:
ˆ L ˆ L ˆ 180 0 L 1 2 3
试列出条件方程 解：t=2p-q-4=4，r=n-t=9-4=5 条件方程为：
ˆ L ˆ L ˆ 1800 0 L 1 2 3 ˆ L ˆ L ˆ 1800 0 L 4 5 6 ˆ L ˆ L ˆ 1800 0 L
7 8 9
ˆ L ˆ L ˆ 3600 0 L 3 6 9 ˆ sin L ˆ sin L ˆ sinL 1 4 7 1 ˆ ˆ ˆ sinL sin L sin L
第五章：条件平差
4.基础方程的解
将改正数方程代入改正数条件方程，得
AQAT K W 0
令 则有
N aa AQAT AP1 AT
N aa K W 0 ——联系数法方程
秩 RN aa RAQAT RA r ，即 N aa 是个r阶的满秩方阵，由此 可解出
试按条件平差法求C、D点高程的平差值。 解：此例 n=4，t=2，r=n-t=2，可列出两个条件方程。 （1）列条件方程：

条件平差

条件平差

1
线性化，并经整理后得
[ctga1 ctg(a1 b1 )]va1 ctg(a1 b1 )vb1 ctga2va2 ctgb2vb2 ctg(a3 b3 )va3 [ctg(a3 b3 ) ctgb3 ]vb3 w 0
w (1 sin(a1 b1 ) sin b2 sin b3 )
主要内容
第一节 条件平差原理 第二节 条件方程 第三节 精度评定 第四节 水准网平差示例
第1页/共37页
第一节 条件平差原理 （ ） 介绍条件平差原理，给出计算公式
一、基础方程及其解
设有r个观测值平差值线性条件方程：
ALˆ A 0 a1Lˆ1
a2 Lˆ2
...Βιβλιοθήκη an Lˆna00
b1Lˆ1 b2 Lˆ2 ... bn Lˆn b0 0（ 4－1－5），矩阵形式为：
...
sin a1 sin a2 sin b1 sin b2
sin a3 sin b3
ctgb3
vb3
0
ctga1va1
...
ctga3va3
ctgb1vb1
... ctgb3vb3
(1 sin a1 sin a2 sin a3 ) 0
sin b1 sin b2 sin b3 第21页/共37页
..................................
0
r1Lˆ1 r2 Lˆ2 ... rn Lˆn r0
0
注意：第一个条件方程系数到最后一个条件方程系数分别 采用字母a-r,下标与观测值编号对应。r是最后一个条件方 程的编号，表示条件方程个数为r，但是r数目与r在英文字 母中序号无关。
求其一阶偏导数，并令其为0：

第3章条件平差原理

第3章条件平差原理

v1 v2 v3 v4


573233

730305

1265125
1043317
推导如下：
VTPV VTP(P1ATK) VTATK(AV )TKWTK
纯量形式
20.09.2019 4
第三章 条件平差
第一节 条件平差原理
二、精度评定
则上述方程可表示为：
2. L、 W 、 K 、 V、 L ˆ的协因数阵及互 协因数阵
LL
W (A L A 0) A L A 0
DFFˆ02QFF
函数的方差
为了检查平差计算的正确性，可以将平差值代入平差值条件方程式，看是否满足 方程关系。
20.09.2019 10
第三章 条件平差
第一节 条件平差原理
[例3-1] n=4 t=3 r=1
A 1 P A TKW 0
p1
1

P
p2

1

n,n
Lˆ
n ,1


Lˆ Lˆ
1 2



Lˆ
n

L LV
n,1 n,1 n,1

Lˆ Lˆ
1 2



L1

பைடு நூலகம்
L
2


v1
v
2



Lˆ
n


L
n

vn

p1 P n,n
p2

kb


rr

第六章 条件平差

第六章 条件平差

CD BD AD Sin(a 2) Sin(a1) Sin(a3) • • = • • =1 BD AD CD Sin(b 2) Sin(b1) Sin(b3)
列条件的原则：将复杂图形分解成典型图形。
类型：图形条件、 极条件、 类型：图形条件、圆周条件 、极条件、固定方位 条件、固定边长条件、 条件、固定边长条件、固定坐标条件
三角形
t = 2*3 − 4 = 2 r = 3 − 2 =1
大地四边形
中心多边形
扇形
t = 2* 4 − 4 = 4 r = 8−4 = 4
t = 2*7 − 4 =10 r =18 −10 = 8 = k +2
t = 2*5 − 4 = 6 r =11− 6 = 5 = k +1
A
2 1 3
C
W = a11L1 + a12L2 + ⋅ ⋅ ⋅ + a1nLn + a10 1 W2 = a 21L1 + a 22L2 + ⋅ ⋅ ⋅ + a 2nLn + a 20 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ Wr = a r1L1 + a r2L2 + ⋅ ⋅ ⋅ + a rn Ln + a r0
r.nn.1 r.1 r,1 2 DLL = σ0 QLL n,n n,n 2 = σ0 −1 P LL n,n
条件平差计算步骤： 三、条件平差计算步骤：
1．根据平差问题的具体情况，列出条件方程， 根据平差问题的具体情况，列出条件方程， 条件方程的个数等于多余观测数r 条件方程的个数等于多余观测数r。 组成法方程式， 2．组成法方程式，法方程的个数等于多余观 测数r 测数r 解法方程，求出联系数K 3．解法方程，求出联系数K值。 代入改正数方程式，求出V 4．将K代入改正数方程式，求出V值，并求 出观测值的平差值=L+V =L+V。 出观测值的平差值=L+V。 检验平差计算的正确性（ 5．检验平差计算的正确性（可用平差值重新 列出平差值条件方程式， 列出平差值条件方程式，看其是否满足方 程）。

第03章 条件平差

第03章 条件平差

zqz99@
设观测值的权阵P为n×n的对角阵，又设联系
数矩阵K＝(ka，kb，…，kr)T，则式(3-11)可用矩阵表 示为： Φ＝VTPV－2KT(AV＋W) 为求新函数Φ的极值，对上式的变量V求其一阶
偏导数，并令其为零。即
d d (V T PV ) d ( 2 K T ( AV W )) dV dV dV
zqz99@
2.1条件平差概述
在图3-1中，设HA为A点的已知高程，为了确定B、C 两点的高程，只要观测两个高差就够了，即必要观测数 为t＝2，而图中按箭头方向观测了h1、h2、h3三个高差， 则n＝3，因为有了多余观测(r＝1)，所以三个观测高差的 平差值产生了一个条件，即 ˆ h ˆ h ˆ 0 h
zqz99@
zqz99@
zqz99@
zqz99@
条 件 制约和影响事物存在、发展的
外部因素
zqz99@
第三章
1
2 3 4 5 6

条件平差
§1 条件平差原理
§2 必要观测与多余观测 §3 条件方程 §4 条件平差方程式 §5 条件平差的精度评定 §6 条件平差举例
式(3-13)称为改正数方程
vi
1 (ai ka bi kb ri kr ) pi
(3-13)
zqz99@
若多余观测为2， 即条件方程只有2个， 改正数方程为:
若多余观测为3， 即条件方程只有3个， 改正数方程为:
vi
v1
1 (ai ka bi kb ) pi
vi
v1
1 (ai ka bi kb ci kc ) pi
1 (a1ka b1kb ) p1 1 v2 (a2 ka b2 kb ) p2 1 vn (an ka bn kb ) pn
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
n ,1 n , n n , r r ,1
得法方程： AQATK-W=0 T 1 T N AQA AP A 令 aa r .r r .nn.nn.r 则有： NaaK-W=0
法方程系数阵Naa是一个r阶的满秩方阵，且可逆
N11k1 N12k 2 N1r k r W1 0 N 21k1 N 22k 2 N 2 r k r W2 0 N r1k1 N r 2 k 2 N rn k r Wr 0
目标函数：f x min n1 x a h x min F a , x f 1k 约束条件： h x 0 k 1 n1 F a, x
0 a F a, x 0 x

L2
L4 L1 L3 L2
A
B
C
§6-2 条件方程
条件方程的个数等于多余观测数r。条件方程之间 不能线性相关,在一个平差问题中，条件方程的个 数是固定不变的.
一、r的确定： r=n-t 二、条件方程的列立： 原则：足数（r个），线性无关，形式简单，易 于列立
控制网常见几何模型
水准网 三角网(测角网) 三边网(测边网) GPS基线向量网 单一附合导线
由此可得联系数K的解：
r ,1
K ( AQA ) W
T
T 1
V QA K
条件平差的 最小二乘解：
n,1
ˆ L V L
三、条件平差计算步骤：
1．根据平差问题的具体情况，列出条件方程，条 件方程的个数等于多余观测数r。 2．组成法方程式，法方程的个数等于多余观测数r 3．解法方程，求出联系数K值。 4．将K代入改正数方程式，求出V值，并求出观测 值的平差值=L+V。 5．检验平差计算的正确性（可用平差值重新列出 平差值条件方程式，看其是否满足方程）。
W1 a 11L1 a 12 L 2 a 1n L n a 10 W2 a 21L1 a 22 L 2 a 2n L n a 20 Wr a r1L1 a r2 L 2 a rn L n a r0
A
h1
h4
C
D
h2
h3
B
解: n=4,t=2,r=2 列两个条件方程式：
ˆ h ˆ h ˆ H 0 HA h 1 2 3 B ˆ h ˆ 0 h
2 4
v1 v 0 1 1 1 0 2 0 1 0 1 v 4 0 3 v4
几个概念：
t个必要观测元素间不存在函数关系；
当存在多余观测，且n个观测值中包含t 个必要观测元素时，观测值间可建立函 数关系。 一个几何模型中有r个多余观测，则在n个 观测值间可产生r个条件方程。
确定三角形的形状
L1=42°12´20"
L2=8°09´09
L3=59°38´40
" "
一个几何模型中有r个多余观测，则在n个观测 值间可产生r个条件方程。
K N W 1 2.5 4 1.74
1 aa
条件观测平差 5 1 0 0.35
1
A
h1
h4 C
D
h3
0 2 1 0.7 h2 1 1 1 0 . 35 1 . 4 V P 1 AT K (m m) 2 1 0 1.74 0.7 1.5 0 1 2.6
闭合差或 不符值
设：
a11 a12 a21 a22 A a a r1 r2
ˆ1 L ˆ2 L ˆ L L ˆ n
a1n a2 n arn
B
ˆ 1.0047 h 1 ˆ h2 1.5174 ˆ L L V ( m) ˆ h3 2.5127 h ˆ 1 . 5174 4
ˆ 11.0083 HC H A h m 1
3 V QAT K 3 3
ˆ L ˆ L ˆ 1800 0 L 1 2 3
条件平差的概念与平差模型：
条件平差法是在满足r个条件方程要求下， 根据最小二乘原理VTPV=min，按求函数的 条件极值的方法，求出观测量的改正数V， 进而求出观测的最或然值（平差值）。
L1 L2 L L n
W1 V1 W2 V2 W , V W V r r
a10 a20 A0 a ro
N aa
2 0 P 0 0
0 1 0 0
0 0 0 0 2 0 0 1.5
2 1 0 1 1 1 0 1 1 1 5 1 1 T AP A 0 1 0 1 2 1 0 1 2.5 1.5 0 1
系数和常数项随不同平差问题取不同的值，它们与观测值无关。
ˆ L V L
建立条件方程：
a11V1 a12V2 a1nVn W1 0 a21V1 a22V2 a2 nVn W2 0 ar1V1 ar 2V2 arnVn Wr 0
一）水准网：t=p 或t=p-1
t 3 C r n t 7 3 4
h1 h 2 h3 ( H C H A ) 0 h1 h6 h7 ( H B H A ) 0 h7 h5 h 4 ( H D H B ) 0 h 2 h5 h6 0
检核平差值满足条件方程
ˆ h ˆ 12.5257 HD H A h m 1 4
例：一条闭合水准路线，已知A点的高程为16.330m, 水准路线上有三个固定点1， 2， 3，高差与测站数如图示, 采用条件平差求各点高程的平差值。
h1=+1.596m n1=3
A
1 h2=-0.231m
h4=-5.642m n4=6
将Ф对V求一阶导数，并令其为零，得 d 2V T p 2 K T A 0 dV 两边转置：PV=ATK， 得改正数V的计算公式为 V=P-1ATK=QATK 改正数方程 条件平差的 AV W 0 由基础方程解出的V不 r .nn.1 r .1 r ,1 基础方程： 仅能消除闭合差，也必 T V QA K 能满足函数最小值条件。
第六章
条件平差
§6-1 条件平差原理
一、引例：按条件平差法求观测内角的平差值。
L1=42°12´20"
L2=78°09´09
L3=59°38´40
" "
拉格朗日乘数法(Lagrange Multiplier)
目的：将等式约束的条件极值转化为无条件极值进行求解。
定义：寻找变量受一个或多个条件所限制的多元函数的极值的方 法。将一个有n个变量与k个约束条件的最优化问题，转换为一 个有n+k个变量的方程组的极值问题，其变量不受任何约束。 增加的k个变量未知数称为拉格朗日乘数，也称为联系数向量。
检核！
例：图中, A, B为已知水准点，其高程 为：H A 12 .013 m, H B 10 .013 m。 为了确定 C , D点的高程，观测了四段 高差 高差观测值与水准路线 的距离如下：
h1 1.004 m, S1 2km, h2 1.516 m, S 2 1km h3 2.512 m, S 3 2km, h4 1.520 m, S1 1.5km 求C和D点高程的平差值。
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
A
h1
C
E
h6
h7 h2 h5 h3
G
h4
F
B
D
t C r n t 8 4 4
A h6
条件观测平差 4
h 6 h5 h 7 0 h1 h 3 h 6 0 h 3 h 2 h 4 0 h 4 h8 h 5 0
条件观测平差
L3
ˆ L ˆ L ˆ 1800 0 L 1 2 3
ˆ L V L i i i
L1
N aa
1 AQAT 1 1 11 3 1
1 K Naa W 3
检核
4201217 ˆ L V 780 0906 L 590 3837
条件方程个数等于多余观测数r＝n-t，n为 观测值总数，t为要观测数。
二、条件平差原理
对某一平差问题，有n个观测量L，t个必要观测 值，多余观测量为r。 在Li间建立 r 个平差值线性条件方程：
ˆ1 a12 L ˆ2 a1n L ˆn a10 0 a11 L ˆ1 a22 L ˆ 2 a2 n L ˆn a20 0 a21 L ˆ1 ar 2 L ˆ2 arn L ˆ n ar 0 0 ar 1 L
ˆ A 0 A L 有： → 0 AV W 0 r , n n ,1 r ,1
r ,1
r .nn.1 T r .1
r ,1
V PV min
根据最小二乘原理，按求函数极值的拉格朗日乘 数法，设 k=(k1,k2,…,kr)T，称为联系数向量（拉格 朗日乘数），组成函数
V T PV 2K T ( AV W )
n2=4
2 h3=+4.256m n3=12
3

例：A、B、C三点在一直线上，测出了AB、BC、 AC的距离，得4个独立观测值：