第 六 章 附有参数的条件平差
- 格式:ppt
- 大小:1.21 MB
- 文档页数:49

《误差理论与测量平差基础》授课教案2006~2007第一学期测绘工程系2006年9月课程名称:误差理论与测量平差基础英文名称:课程编号:??适用专业:测绘工程总学时数: 56学时其中理论课教学56学时,实验教学学时总学分:4学分◆内容简介《测量平差》是测绘工程等专业的技术基础课,测量平差的任务是利用含有观测误差的观测值求得观测量及其函数的平差值,并评定其精度。
本课程的主要内容包括误差理论﹑误差分布与精度指标﹑协方差传播律及权﹑平差数学模型与最小二乘原理﹑条件平差﹑附有参数的条件平差﹑间接平差﹑附有限制条件的间接平差﹑线性方程组解算方法﹑误差椭圆﹑平差系统的统计假设检验和近代平差概论等。
◆教学目的、课程性质任务,与其他课程的关系,所需先修课程本课程的教学目的是使学生掌握误差理论和测量平差的基本知识、基本方法和基本技能,为后续专业课程的学习和毕业后从事测绘生产打下专业基础。
课程性质为必修课、考试课。
本课程的内容将在测绘工程和地理信息系统专业的专业课程的测量数据处理内容讲授中得到应用,所需先修课程为《高等数学》、《概率与数理统计》、《线性代数》和《测量学》等。
◆主要内容重点及深度考虑到专业基础理论课教学应掌握“必须和够用”的原则,结合测绘专业建设的指导思想,教学内容以最小二乘理论为基础,误差理论及其应用、平差基本方法与计算方法,以及平差程序设计及其应用为主线。
测量误差理论,以分析解决工程测量中精度分析和工程设计的技术问题为着眼点,在掌握适当深度的前提下,有针对性的加强基本理论,并与实践结合,突出知识的应用。
平差方法,以条件平差和参数平差的介绍为主,以适应电算平差的参数平差为重点。
计算方法,以介绍适应电子计算机计算的理论、方法为主,建立新的手工计算与计算机求解线性方程组过程相对照的计算方法和计算格式。
平差程序设计及其应用,通过课程设计要求学生利用所学程序设计的知识和平差数学模型编制简单的平差程序,熟练掌握已有平差程序的使用方法。

附有系统参数的平差及其参数显著性检验摘要:通过对测量误差中系统误差影响及重要性的分析,对附有系统参数平差原理进行了探讨,得出了其平差数学模型和系统参数显著性检验的方法,最后利用某实测数据进行验证计算。
关键字:系统参数;平差;显著性检验1.引言观测误差按性质分为三种成分:粗差、系统误差、偶然误差。
但在经典平差中,通常假定观测值中仅包含系统误差。
经典平差中是假定观测误差中不含有系统误差,但测量实践证明,尽管在观测过程中会采用各种观测措施减少系统误差,并在观测后对观测数据进行了必要的处理,但难以避免观测值中仍含有系统误差。
因此,在平差前完全剔除粗差和消除系统误差的影响是不可能的。
随着测量精度的不断提高,对平差结果的精度要求也愈来愈高,近年来出现了通过平差剔除粗差和消除系统误差对平差结果影响的方法。
传统上剔除观测值的粗差,通常是在平差之前进行,比如采用避免粗差的观测程序,增加多余观测,以及用几何条件闭合差控制粗差等,尽管采用这些措施,一些小的粗差仍然是不可避免的。
1968年,巴尔达(W.Baarda)在他的名著《大地网的检验方法》中,首先用数理统计方法阐述了测量系统的可靠性理论和检验粗差的“数据探测(Data-Snooping)”法。
为在平差过程中自动剔除粗差提供了理论基础;而对平差过程中消除系统误差对平差结果影响的方法,在航空摄影测量学中称为自检校平差。
这种平差方法的基本思想是,在仅含偶然误差模型式的基础上,加入一些附加参数(或称系统参数)用以补偿在观测数据中存在的系统误差对平差结果的影响。
但在函数模型中加入附加参数后,可能会引起附加参数之间或附加参数与基本参数之间的强相关,而使法方程性质恶化,为使法方程性质不致变坏,应剔除一些参数。
附加参数的统计检验就是解决这个问题的。
随着对测量精度的要求越来越高,一些精密工程测量中考虑了系统参数对平差结果的影响。
比如在高速铁路的CPIII测量中、大型GPS网的监测等。


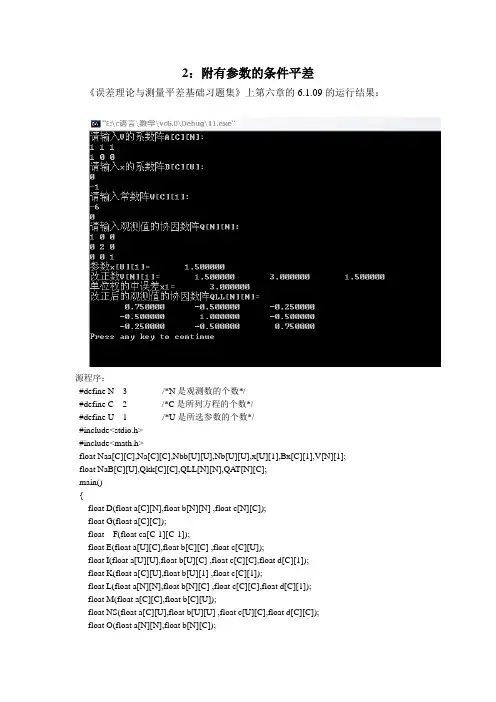
2:附有参数的条件平差《误差理论与测量平差基础习题集》上第六章的6.1.09的运行结果:源程序:#define N 3 /*N是观测数的个数*/#define C 2 /*C是所列方程的个数*/#define U 1 /*U是所选参数的个数*/#include<stdio.h>#include<math.h>float Naa[C][C],Na[C][C],Nbb[U][U],Nb[U][U],x[U][1],Bx[C][1],V[N][1];float NaB[C][U],Qkk[C][C],QLL[N][N],QA T[N][C];main(){float D(float a[C][N],float b[N][N] ,float c[N][C]);float G(float a[C][C]);float F(float ca[C-1][C-1]);float E(float a[U][C],float b[C][C] ,float c[C][U]);float I(float a[U][U],float b[U][C] ,float c[C][C],float d[C][1]);float K(float a[C][U],float b[U][1] ,float c[C][1]);float L(float a[N][N],float b[N][C] ,float c[C][C],float d[C][1]);float M(float a[C][C],float b[C][U]);float NS(float a[C][U],float b[U][U] ,float c[U][C],float d[C][C]);float O(float a[N][N],float b[N][C]);float S(float a[N][C],float b[C][C] ,float c[C][N],float d[N][N]); float DM(float a[1][N],float b[N][N] ,float c[N][1]);float A[C][N],AT[N][C],B[C][U],BT[U][C];float W[C][1],Q[N][N],P[N][N],NaBT[U][C];float AQ[C][N],VT[1][N],g,f,g1,f1;float g2,g3,g4,g5,g6,g7,g8,x1;int i,j,m;printf("请输入V的系数阵A[C][N]:\n");for(i=0;i<C;i++)for(j=0;j<N;j++)scanf("%8f",&A[i][j]);printf("请输入x的系数阵B[C][U]:\n");for(i=0;i<C;i++)for(j=0;j<U;j++)scanf("%8f",&B[i][j]);printf("请输入常数阵W[C][1]:\n");for(i=0;i<C;i++)for(j=0;j<1;j++)scanf("%8f",&W[i][j]);printf("请输入观测值的协因数阵Q[N][N]:\n");for(i=0;i<N;i++)for(j=0;j<N;j++)scanf("%8f",&Q[i][j]);for(i=0;i<N;i++)for(j=0;j<N;j++)P[i][j]=Q[i][j];for(i=0,j=0;i<N&j<N;i++,j++)P[i][j]=1.0/P[i][j];for(i=0;i<C;i++)for(j=0;j<N;j++)A T[j][i]=A[i][j];for(i=0;i<C;i++)for(j=0;j<U;j++)BT[j][i]=B[i][j];g=D(A,Q,AT);f=G(Naa);for(i=0;i<C;i++)for(j=0;j<C;j++)Na[i][j]=(Na[i][j]/f);g1=E(BT,Na,B);Nb[0][0]=1.0/g1;g2=I(Nb,BT,Na,W);for(i=0;i<U;i++)x[i][0]=(-1)*x[i][0];g3=K(B,x,W);g4=L(Q,AT,Na,Bx);for(i=0;i<N;i++)V[i][0]=(-1)*V[i][0];for(i=0;i<N;i++)VT[0][i]=V[i][0];x1=DM(VT,P,V);x1=x1/(C-U);g5=M(Na,B);for(i=0;i<C;i++)for(j=0;j<U;j++)NaBT[j][i]=NaB[i][j];g6=NS(NaB,Nb,NaBT,Na);g7=O(Q,AT);for(i=0;i<N;i++)for(j=0;j<C;j++)AQ[j][i]=QAT[i][j];g8=S(QAT,Qkk,AQ,Q);printf("参数x[U][1]=");for(i=0;i<U;i++)printf("%15f",x[i][0]);printf("\n改正数V[N][1]=");for(i=0;i<N;i++)printf("%15f",V[i][0]);printf("\n单位权的中误差x1=%15f",sqrt(x1));printf("\n改正后的观测值的协因数阵QLL[N][N]=\n");for(i=0;i<N;i++){for(j=0;j<N;j++)printf("%15f",QLL[i][j]);printf("\n");}}float D(float a[C][N],float b[N][N] ,float c[N][C]){int i,j,m;float d[C][N];for(i=0;i<C;i++)for(j=0;j<N;j++){d[i][j]=a[i][0]*b[0][j];for(m=1;m<N;m++)d[i][j]+=(a[i][m]*b[m][j]);}for(i=0;i<C;i++)for(j=0;j<C;j++){Naa[i][j]=d[i][0]*c[0][j];for(m=1;m<N;m++)Naa[i][j]+=(d[i][m]*c[m][j]);}return (Naa[0][0]);}float G(float a[C][C]){int i,j,m,n;float c[C-1][C-1],y=0;for(i=0;i<C;i++)for(j=0;j<C;j++){for(m=0;m<C;m++)for(n=0;n<C;n++){if(m<i&&n<j)c[m][n]=a[m][n];if(m>i&&n<j)c[m-1][n]=a[m][n];if(m<i&&n>j)c[m][n-1]=a[m][n];if(m>i&&n>j)c[m-1][n-1]=a[m][n];}if((i+j)%2==0)Na[j][i]=F(c);elseNa[j][i]=(-1)*F(c);}for(m=0;m<C;m++)y+=(a[0][m]*Na[m][0]);return (y);}float F(float ca[C-1][C-1]){int i,j,m,n,s,t,k=1;float f=1,c,x,sn;for (i=0,j=0;i<C-1&&j<C-1;i++,j++) {if (ca[i][j]==0){for (m=i;ca[m][j]==0;m++);if (m==C-1){sn=0;return (sn);}elsefor (n=j;n<C-1;n++){c=ca[i][n];ca[i][n]=ca[m][n];ca[m][n]=c;}k*=(-1);}for (s=C-2;s>i;s--){x=ca[s][j];for (t=j;t<C-1;t++)ca[s][t]-=ca[i][t]*(x/ca[i][j]);}}for (i=0;i<C-1;i++)f*=ca[i][i];sn=k*f;return (sn);}float E(float a[U][C],float b[C][C] ,float c[C][U]) {int i,j,m;float d[U][C];for(i=0;i<U;i++)for(j=0;j<C;j++){d[i][j]=a[i][0]*b[0][j];for(m=1;m<C;m++)d[i][j]+=(a[i][m]*b[m][j]);}for(i=0;i<U;i++)for(j=0;j<U;j++){Nbb[i][j]=d[i][0]*c[0][j];for(m=1;m<C;m++)Nbb[i][j]+=(d[i][m]*c[m][j]);}return (Nbb[0][0]);}float I(float a[U][U],float b[U][C] ,float c[C][C],float d[C][1]) {int i,j,m;float dd[U][C],e[U][C];for(i=0;i<U;i++)for(j=0;j<C;j++){dd[i][j]=a[i][0]*b[0][j];for(m=1;m<U;m++)dd[i][j]+=(a[i][m]*b[m][j]);}for(i=0;i<U;i++)for(j=0;j<C;j++){e[i][j]=dd[i][0]*c[0][j];for(m=1;m<C;m++)e[i][j]+=(dd[i][m]*c[m][j]);}for(i=0;i<U;i++)for(j=0;j<1;j++){x[i][j]=e[i][0]*d[0][j];for(m=1;m<C;m++)x[i][j]+=(e[i][m]*d[m][j]);}return (x[0][0]);}float K(float a[C][U],float b[U][1] ,float c[C][1]){int i,j,m;float d[C][1];for(i=0;i<C;i++)for(j=0;j<1;j++){d[i][j]=a[i][0]*b[0][j];for(m=1;m<U;m++)d[i][j]+=(a[i][m]*b[m][j]);}for(i=0;i<C;i++)Bx[i][0]=(d[i][0]+c[i][0]);return (Bx[0][0]);}float L(float a[N][N],float b[N][C] ,float c[C][C],float d[C][1]) {int i,j,m;float dd[N][C],e[N][C];for(i=0;i<N;i++)for(j=0;j<C;j++){dd[i][j]=a[i][0]*b[0][j];for(m=1;m<N;m++)dd[i][j]+=(a[i][m]*b[m][j]);}for(i=0;i<N;i++)for(j=0;j<C;j++){e[i][j]=dd[i][0]*c[0][j];for(m=1;m<C;m++)e[i][j]+=(dd[i][m]*c[m][j]);}for(i=0;i<N;i++)for(j=0;j<1;j++){V[i][j]=e[i][0]*d[0][j];for(m=1;m<C;m++)V[i][j]+=(e[i][m]*d[m][j]);}return (V[0][0]);}float M(float a[C][C],float b[C][U]){int i,j,m;for(i=0;i<C;i++)for(j=0;j<U;j++){NaB[i][j]=a[i][0]*b[0][j];for(m=1;m<C;m++)NaB[i][j]+=(a[i][m]*b[m][j]);}return (NaB[0][0]);}float NS(float a[C][U],float b[U][U] ,float c[U][C],float d[C][C]) {int i,j,m;float dd[C][U],e[C][C];for(i=0;i<C;i++)for(j=0;j<U;j++){dd[i][j]=a[i][0]*b[0][j];for(m=1;m<U;m++)dd[i][j]+=(a[i][m]*b[m][j]);}for(i=0;i<C;i++)for(j=0;j<C;j++){e[i][j]=dd[i][0]*c[0][j];for(m=1;m<U;m++)e[i][j]+=(dd[i][m]*c[m][j]);}for(i=0;i<C;i++)for(j=0;j<C;j++)Qkk[i][j]=(d[i][j]-e[i][j]);return (Qkk[0][0]);}float O(float a[N][N],float b[N][C]){int i,j,m;for(i=0;i<N;i++)for(j=0;j<C;j++){QAT[i][j]=a[i][0]*b[0][j];for(m=1;m<N;m++)QAT[i][j]+=(a[i][m]*b[m][j]);}return (QAT[0][0]);}float S(float a[N][C],float b[C][C] ,float c[C][N],float d[N][N]) {int i,j,m;float dd[N][C],e[N][N];for(i=0;i<N;i++)for(j=0;j<C;j++){dd[i][j]=a[i][0]*b[0][j];for(m=1;m<C;m++)dd[i][j]+=(a[i][m]*b[m][j]);}for(i=0;i<N;i++)for(j=0;j<N;j++){e[i][j]=dd[i][0]*c[0][j];for(m=1;m<C;m++)e[i][j]+=(dd[i][m]*c[m][j]);}for(i=0;i<N;i++)for(j=0;j<N;j++)QLL[i][j]=(d[i][j]-e[i][j]);return (QLL[0][0]);}float DM(float a[1][N],float b[N][N] ,float c[N][1]){int i,j,m;float d[1][N],x;for(i=0;i<1;i++)for(j=0;j<N;j++){d[i][j]=a[i][0]*b[0][j];for(m=1;m<N;m++)d[i][j]+=(a[i][m]*b[m][j]);}for(i=0;i<1;i++)for(j=0;j<1;j++){x=d[i][0]*c[0][j];for(m=1;m<N;m++)x+=(d[i][m]*c[m][j]);}return (x);}程序说明:1) 用该程序前,根据具体情况输入N,C和U;2) 该程序所选参数的个数U必须为1,因为求阶数为1的行列式的逆就是这个数的倒数,而阶数大于1是,逆不能这样求。


第一章测试1.误差是不可避免的。
A:对B:错答案:A2.构成观测条件的要素有哪些A:外界条件B:计算工具C:观测者D:测量仪器答案:ACD3.对中误差属于那种误差A:系统误差B:偶然误差C:不是误差D:粗差答案:B第二章测试1.两随机变量的协方差等于0时,说明这两个随机变量A:相关B:互不相关C:相互独立答案:B2.观测量的数学期望就是它的真值A:错B:对答案:A3.衡量系统误差大小的指标为A:精确度B:准确度C:不确定度D:精度答案:B4.精度是指误差分布的密集或离散程度,即离散度的大小。
A:错B:对答案:B5.若两观测值的中误差相同,则它们的A:测量仪器相同B:真误差相同C:观测值相同D:精度相同答案:D第三章测试1.设L的权为1,则乘积4L的权P=()。
A:1/4B:4C:1/16D:16答案:C2.有一角度测20测回,得中误差±0.42秒,如果要使其中误差为±0.28秒,则还需增加的测回数N=()。
A:25B:45C:20D:5答案:A3.在水准测量中,设每站观测高差的中误差均为1cm,今要求从已知点推算待定点的高程中误差不大于5cm,问可以设25站。
A:对B:错答案:A4.已知距离AB=100m,丈量一次的权为2,丈量4次平均值的中误差为2cm,若以同样的精度丈量CD的距离16次,CD=400m,则两距离丈量结果的相对中误差分别为( 1/5000 )、(1/20000 )。
A:错B:对答案:B5.A:29B:35C:5D:25答案:D第四章测试1.当观测值为正态随机变量时,最小二乘估计可由最大似然估计导出。
A:对B:错答案:A2.多余观测产生的平差数学模型,都不可能直接获得唯一解。
A:对B:错答案:A3.在平差函数模型中,n、t、r、u、s、c等字母各代表什么量?它们之间有何关系?( n观测值的个数 )(t必要观测数 )(r多余观测数,r=n-t )(u所选参数的个数 )( s非独立参数的个数,s=u-t )( c所列方程的个数,c=r+u )A:对B:错答案:A4.A:对B:错答案:A5.A:错B:对答案:B第五章测试1.关于条件平差中条件方程的说法正确的是:A: 这r个条件方程应彼此线性无关B: 应列出r个条件方程C: r个线性无关的条件方程必定是唯一确定的,不可能有其它组合。