材料力学第三章-03 纯剪切
- 格式:docx
- 大小:5.75 MB
- 文档页数:3

第3章 剪切与扭转提要:本章将讨论杆件的剪切和扭转这两种基本变形。
F。
为了保证连接件的正常剪切是杆件的基本变形之一,杆件横截面上的内力为剪力Q工作,一般需要进行连接件的剪切强度、挤压强度计算。
本章将探讨采用实用计算法来进行简化计算。
扭转也是杆件的基本变形之一。
杆件横截面上的内力偶矩为扭矩T。
本章将根据传动轴的功率P和转速n来计算杆件所承受的外力偶矩,并通过截面法来计算扭矩;还将探讨扭矩图的绘制方法。
本章将研究薄壁圆筒的扭转变形及其横截面上的切应力分布,并由薄壁圆筒的扭转实验推出剪切胡克定律,还要探讨切应力互等定理。
为了保证杆件在受扭情况下能正常工作,除了要满足强度要求外,还须满足刚度要求。
本章将从变形几何关系、物理关系和静力学关系三方面入手导出等直圆杆扭转时横截面上的切应力公式,并以之为基础建立扭转的强度条件;同时在研究等直圆杆扭转变形的基础上,建立扭转的刚度条件。
本章还将探讨杆件斜截面上的应力分布。
本章研究等直圆杆的扭转仅限于线弹性范围内,且材料符合胡克定律,并以平面假设为基本依据。
在实际工程中,有时也会遇到非圆截面等直杆的扭转问题。
本章将简单介绍矩形截面杆、开口薄壁截面杆和闭口薄壁截面杆的自由扭转问题。
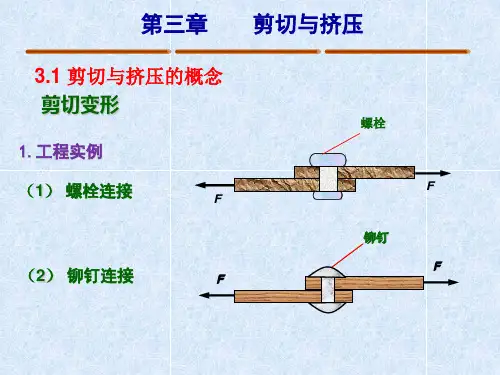
3.1 剪切3.1.1 剪力和切应力剪切(shear)是杆件的基本变形之一,其计算简图如图3.1(a)所示。
在杆件受到一对相距很近、大小相同、方向相反的横向外力F的作用时,将沿着两侧外力之间的横截面发生相对错动,这种变形形式就称为剪切。
当外力F足够大时,杆件便会被剪断。
发生相对错动的横截面则称为剪切面(shear surface)。
既然外力F使得剪切面发生相对错动,那么该截面上必然会产生相应的内力以抵抗变形,这种内力就称为剪力(shearing force),用符号F表示。
运用截面法,可以很容易地分析Q出位于剪切面上的剪力F与外力F大小相等、方向相反,如图3.1(b)所示。
材料力学中通Q常规定:剪力F对所研究的分离体内任意一点的力矩为顺时针方向的为正,逆时针方向的Q为负。





直升机的旋转轴
电机每秒输入功:外力偶作功完成:
×
=P W
M W
e
⋅
=
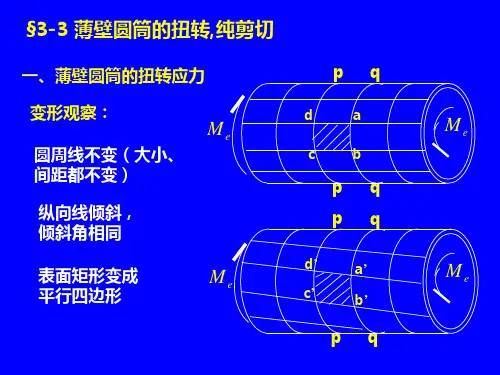
形状、大小、间距不变,各圆周线只是绕轴线转动了一个角度。
倾斜了同一个角度,小方格变成了平行四边形。
τdα
τ
l
ϕ
做薄壁圆筒的扭转试验可得
l
是材料的一个弹性常数,称为剪切弹性模量,G的量纲各向同性材料,三个弹性常数之间的关系:
ρργγtg ≈x
d d d ′=x d d ϕρ⋅=O 1O 2ABCD 为研究对象
D’
微段扭转变形d dx Rd dx DD tg ϕγγ==≈'d ϕ/ d x -扭转角沿x 轴的变化率
扭转变形计算式
O d A ρTρ⋅
(实心截面)
1、横截面上角点处,切应力为零;
2、横截面边缘各点处,切应力
3、切应力沿横截面周边形成与
4、横截面周边长边中点处,切应力最大。
有关,见教材P93 之表3.2。


第3章 扭转1、扭转的概念:杆件的两端个作用一个力偶,其力偶矩大小相等、转向相反且作用平面垂直于杆件轴线,致使杆件的任意两个横截面都发生绕轴线的相对转动,即为扭转变形。
2、外力偶矩的计算{}{}{}min /95491000602r KW m N e e n P M P M n=⇒⨯=⨯⨯⋅π 式中,e M 为外力偶矩。
又由截面法:e e M T M T =⇒=-0 T 称为n n -截面上的扭矩。
规定:若按右手螺旋法则把T 表示为矢量,当矢量方向与研究部分中截面的外法线的方向一致时,T 为正;反之为负。
3、纯剪切(1)薄壁圆筒扭转时的切应力 δπττδπ222r M r r M ee =⇒••=(2)切应力互等定理:在单元体相互垂直的两个平面上,切应力必然成对存在,且数值相等;两者都垂直于平面的交线,方向则共同指向或背离这一交线。
(3)切应变 剪切胡克定律:当切应力不超过材料的剪切比例极限时,切应变γ与切应力τ成正比。
γτG = G 为比例常数,称为材料的切变模量。
弹性模量E 、泊松比μ和切变模量G 存在关系:)1(2μ+=EG 4、圆轴扭转时的应力(1)变形几何关系:距圆心为ρ处的切应变为dxd ϕργρ=(2)物理关系:ρτ为横截面上距圆心为ρ处的切应力。
dxd G G ϕρτγτρρρ=⇒= (3)静力关系:内力系对圆心的力矩就是横截面的扭矩:dA d d GdA T AxA⎰⎰==2ρρτϕρ 以p I 表示上式右端的积分式:dA I Ap ⎰=2ρ p I 称为横截面对圆心O 点的极惯性矩(截面二次极矩)横截面上距圆心为ρ的任意点的切应力:pI T ρτρ=ρ最大时为R ,得最大切应力:pI TR =max τ引用记号RI W p t =t W 称为抗扭截面系数。
则tW T =max τp I 和t W 的计算(1)实心轴:3224420032D R d d dA I RAp ππθρρρπ====⎰⎰⎰16233D R RI W p t ππ===(2)空心轴:)1(32)(324444202/2/32αππθρρρπ-=-===⎰⎰⎰D d D d d dA I D d Ap)1(16)(164344αππ-=-==D d D DRI W p t5、圆轴扭转时的变形pGI Tl =ϕ ϕ为扭转角,l 为两横截面间的距离。
3-3 纯剪切
刚性圆环绕轴线发生相对转动
8-2 20:00
四、剪切胡克定律
回忆:拉压胡克定律:横截面上正应力和横截面上的点沿着轴线方向线应变之间的关系;切应力和角应变之间的关系;
横截面切应力比不超过比例极限;工作在线弹性范围内
角应变和切应力之间满足胡克定律;
1、A
2、成立剪切胡克定律不成立;
3、对
4、轴的转速越高,直径越大还是越小?
总结
1、受到什么样的外力,构件发生扭转变形;
受到一组力偶矩失与杆件的轴线平行的外力偶发生扭转变形;
2、这样的外力偶在杆件的横截面上产生何种内力?
产生扭矩,其力偶矩失与杆件的轴线平行;
3、在进行扭矩大小计算的时候,要求截面法截开以后要求内
力设正,不管外力偶方向如何,力偶矩失永远远离求内力的截
面。
4、方程:以内力的方向为正,同向相加反向相减。
5、怎么来做扭矩图?
N个外力偶把杆件分成N-1段,两个力偶之间一个截面,两
个外力偶之间内力不变
6、怎么确定危险截面
扭矩偏大,截面尺寸偏小的截面;
7、轴的合理受力问题,什么情况下轴的受力最合理;
最大扭矩绝对值要最小,轴的受力最合理;
8、切应力互等定理?
互相垂直的两个面上切应力成对出现;
切应力方向:同时指向或者同时远离
9、切应力互等定理适用于什么范围?
扭转变形过程中的任何阶段;
10、切应力和产生角应变,剪切胡克定律适用范围?
线弹性范围
做实验;18章4节圆轴的塑性扭转。