静力学方程的应用1

流体静力学方程的应用条件流体静力学是流体力学的一个分支，研究的是静止流体的力学性质和行为。

在实际应用中，流体静力学方程经常用于解决各种与静止流体相关的问题。

下面将介绍流体静力学方程的应用条件及其在不同领域的具体应用。

流体静力学方程适用于稳定的静止流体系统，即系统中的流体没有运动。

这意味着流体的速度、加速度等都为零，只存在压力和重力。

当流体系统处于平衡状态时，流体静力学方程可以用来描述和分析流体的力学性质。

在建筑工程领域，流体静力学方程被广泛应用于水压力计算。

例如，在水坝工程中，需要计算水坝底部受到的压力，以确保水坝的稳定性。

通过应用流体静力学方程，可以计算出水坝底部受到的水压力，并据此设计水坝的结构和厚度，确保其能够承受水压力的作用。

在航空航天领域，流体静力学方程的应用条件也得到了充分利用。

例如，在航空器的燃油系统中，需要保证燃油能够平稳地供给到发动机。

通过应用流体静力学方程，可以计算出燃油供给系统中的压力分布，并据此设计和优化燃油管道的布局和尺寸，以确保燃油能够稳定地输送到发动机。

在地质学领域，流体静力学方程被用于地下水的流动分析。

地下水是地球内部的一种重要水资源，对于地下水的合理开发和利用具有重要意义。

通过应用流体静力学方程，可以计算地下水的压力分布和流速，进而预测地下水的流动方向和速率。

这对于地下水资源的管理和保护具有重要的参考意义。

除了以上几个领域，流体静力学方程还被广泛应用于液压系统、水污染控制、海洋工程等领域。

在液压系统中，流体静力学方程被用于计算液压缸中的压力和力的分布，以实现液压系统的运动控制。

在水污染控制中，流体静力学方程被用于计算污水处理设备中的压力和流速，以实现污水的处理和净化。

在海洋工程中，流体静力学方程被用于计算海洋结构物受到的水压力和力的分布，以确保结构物的安全性和稳定性。

流体静力学方程在各个领域都有着广泛的应用。

通过应用流体静力学方程，可以计算出流体系统中的压力分布和力的分布，进而实现对流体系统的分析和设计。

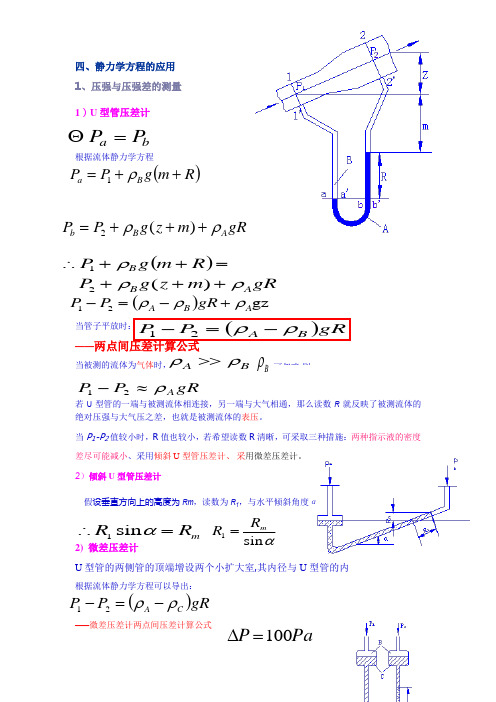
四、静力学方程的应用 1、压强与压强差的测量 1）U 型管压差计根据流体静力学方程当管子平放时： ——两点间压差计算公式当被测的流体为气体时， 若U 型管的一端与被测流体相连接，另一端与大气相通，那么读数R 就反映了被测流体的绝对压强与大气压之差，也就是被测流体的表压。

当P 1-P 2值较小时，R 值也较小，若希望读数R 清晰，可采取三种措施：两种指示液的密度差尽可能减小、采用倾斜U 型管压差计、 采用微差压差计。

2）倾斜U 型管压差计假设垂直方向上的高度为Rm ，读数为R 1，与水平倾斜角度α2) 微差压差计 U 型管的两侧管的顶端增设两个小扩大室,其内径与U 型管的内根据流体静力学方程可以导出： ——微差压差计两点间压差计算公式 ba P P =Θ()R m g P P B a ++=ρ1gRm z g P P A B b ρρ+++=)(2())( 21gR m z g P R m g PA B B ρρρ+++=++∴()gz 21A B A gR P P ρρρ+-=-可忽略,则 B ρB A ρρ>>， gRP P A ρ≈-21()gRP P B A ρρ-=-21m R R =∴αsin 1αsin 1m R R =()gRP P C A ρρ-=-21PaP 100=∆例：用3种压差计测量气体的微小压差试问：1）用普通压差计，以苯为指示液，其读数R 为多少？2）用倾斜U 型管压差计，θ=30°，指示液为苯，其读数R’为多少？3）若用微差压差计，其中加入苯和水两种指示液，扩大 室截面积远远大于U 型管截面积，此时读数R 〃为多少？ R 〃为R 的多少倍？ 已知：苯的密度 水的密度计算时可忽略气体密度的影响。

解：1）普通管U 型管压差计U 型管的两侧管 3/879m kg c=ρg P RC ρ∆=807.9879100⨯=m 0116.0=。

流体静力学方程的应用条件(一)流体静力学方程的应用条件1. 理论背景在研究流体行为时，流体静力学是其中的一个重要方面。

流体静力学是研究流体在静止状态下的行为和力学性质的学科。

通过应用流体静力学方程，我们可以分析和解决许多与流体静停止状态有关的问题。

2. 流体静力学方程的概述流体的静平衡在流体静力学中，我们考虑的是流体处于静止状态，并且没有流动的情况。

这意味着流体内部的每一点都保持静止，并且没有速度梯度存在。

流体静力学方程流体静力学方程是描述流体静力学行为的基本方程，它包括了质量守恒、动量守恒和能量守恒定律。

流体静力学方程可以用来计算流体内的压力分布、压力力学、力的传递以及其他与流体在静止状态下相关的物理量。

3. 流体静力学方程的应用条件根据流体静力学方程的性质和适用范围，我们可以得出以下应用条件：•流体应为牛顿流体：流体力学方程适用于牛顿流体，即粘度随剪切速率保持恒定。

如果流体具有非牛顿性质，例如塑性流体或非牛顿粘性流体，流体静力学方程将不再适用。

•流体应为静止状态：流体静力学方程适用于流体处于静止状态下的情况。

如果流体具有流动或速度梯度，流体动力学方程将更适用于分析此类情况。

•流体应为恒定密度流体：流体静力学方程假设流体具有恒定的密度。

如果流体的密度随位置或时间变化，流体静力学方程将不再适用。

•流体应为亚音速流体：流体静力学方程适用于亚音速流体，即流体的速度小于声速。

如果流体处于超音速流动状态，流体动力学方程将更适合分析。

4. 结论流体静力学方程是解决与流体在静态条件下相关问题的基本工具。

然而，我们必须注意应用流体静力学方程的条件，以确保结果的准确性和可靠性。

只有在满足适用条件的情况下，我们才能有效地利用流体静力学方程解决实际问题。

以上是流体静力学方程的应用条件的简要介绍。

通过理解并应用这些条件，我们可以更好地利用流体静力学方程分析和解决与静态流体行为有关的问题。

5. 应用举例下面列举几个典型的应用例子，展示在何种情况下可以应用流体静力学方程：•管道内的压力分布：当液体在管道内静止时，可以使用流体静力学方程来计算管道内的压力分布。

第二讲流体静力学基本方程及其应用【学习要求】1．理解流体静力学方程的意义；2．掌握流体静力学方程的应用。

【预习内容】1．在均质流体中，流体所具有的与其所占有的之比称为。

任何流体的密度都随它的和而变化，但对液体的密度影响很小，可忽略，故常称液体为的流体。

2．流体静压力的两个重要特性分别是：（1）；（2）。

3．1atm = mmHg = Pa = mH2O【学习内容】一、流体静力学基本方程式1．流体静力学基本方程式的形式p2 = p1+ ρ ( z1—z2 )g 或p2 = p1+ hρg流体静力学方程表明：在重力作用下静止液体内部的变化规律。

即在液体内部任一点的流体静压力等于。

2．流体静力学基本方程式的意义流体静力学方程表明：（1）当作用于流体面上方的压强有变化时；（2）当流体面上方的压强一定时，静止流体内部任一点压强的大小与流体本身的和有关，因此在的的同一液体处，处在都相等。

二、流体静力学基本方程式的应用1．流体进压强的测量（1）U形管压差计①U形管压差计由、及管内指示液组成。

②指示液要与被测流体不，不起，其密度要，通常采用的指示液有、、及等。

③U形管压差计可用来测量压强差，也可以用来测量或。

【典型例题】例1用U形管测量管道中1、2两点的压强差。

已知管内流体是水，指示液是密度为1595 kg／m3的CCl4，压差计读数为40cm，求压强差(p1– p2)。

若管道中的流体是密度为2.5kg／m3的气体，指示液仍为CCl4，U形管读数仍为40cm，则管道中1、2两点的压强差是多少Pa？【例2】某蒸汽锅炉用本题附图中串联的汞-水U形管压差计以测量液面上方的蒸气压。

已知汞液面与基准面的垂直距离分别为h1 = 2.3 m，h2 = 1.2 m,h3 = 2.5 m,h4 = 1.4m,两U形管间的连接管内充满了水。

锅炉中水面与基准面的垂直距离h5 = 3.0m，大气压强p a = 99kPa。

试求锅炉上方水蒸汽的压强p0为若干（Pa）？【随堂练习】1．大气压强为750mmHg时，水面下20m深处水的绝对压强为多少Pa？2．水平导管上的两点接一盛有水银的U形管压差计（如图所示），压差计读数为26mmHg。

流体静力学方程的适用条件(一)流体静力学方程的适用条件引言流体静力学是研究流体在静力平衡状态下的行为规律的学科，描述了流体静力学方程的适用条件对于理解和解决流体的静态问题非常重要。

适用条件在研究流体静力学方程的适用条件时，需要考虑以下几个方面：1.静态平衡条件–流体必须处于静力平衡状态，即没有加速度和剪切力的存在。

–流体内部各点之间的压强相等，即存在等压面。

这要求流体没有外力或外压作用。

2.宏观尺度–流体静力学方程适用于宏观尺度，即适用于大尺度上对流体进行整体平均的情况。

–该方程不适用于涉及微观尺度或有明显界面效应的情况。

3.不可压缩性–流体静力学方程假设流体是不可压缩的，即流体密度在空间和时间上保持不变。

–在某些特殊情况下，对于可压缩流体，可以通过适当的近似方法将其视为不可压缩流体进行处理。

4.没有动力学效应–流体静力学方程适用于没有动力学效应的情况，即流体中没有涡旋运动或渗透流存在。

总结流体静力学方程的适用条件主要包括静态平衡、宏观尺度、不可压缩性和没有动力学效应等。

在理解和应用流体静力学方程时，我们必须考虑这些条件，并根据具体情况进行适当的近似和简化。

这些适用条件是我们研究和解决流体静态问题的基础。

以上是针对流体静力学方程的适用条件的相关介绍，希望能对读者有所帮助。

应用范围流体静力学方程的适用条件在很多领域都有广泛的应用，包括但不限于以下几个方面：1.工程液压学–在液压系统中，通过流体静力学方程可以计算液压系统中的压力分布、液体高度等参数。

–这有助于优化液压系统的设计和运行，提高系统的效率和安全性。

2.建筑水力学–在水资源工程中，流体静力学方程可用于计算大坝、堤坝和水闸等结构的承压能力。

–这可以帮助工程师评估工程结构的稳定性，并制定相应的安全措施。

3.管道输送–在管道系统中，流体静力学方程可用于计算流体在管道中的流速和压力分布。

–这对于优化管道输送系统的设计和运行非常重要，能够提高流体的输送效率和节约能源。