化工原理-流体静力学方程
- 格式:ppt
- 大小:863.50 KB
- 文档页数:28
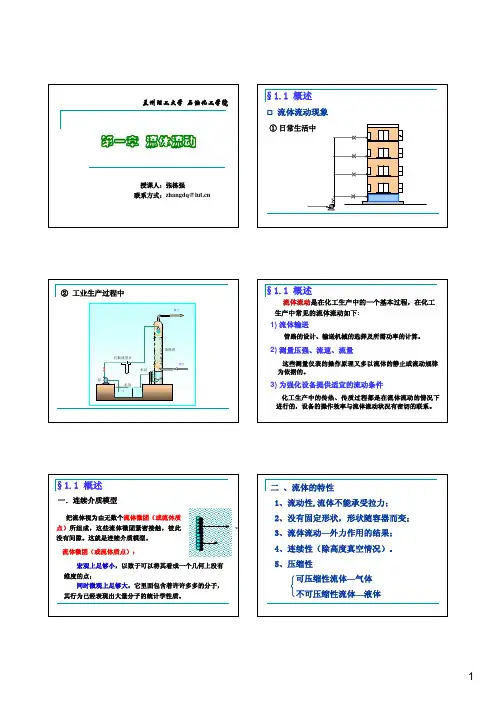
孔板流量计泵水封填料塔水池把流体视为由无数个流体微团(或流体质所组成,这些流体微团紧密接触,彼此没有间隙。
这就是连续介质模型。
流体微团(或流体质点):宏观上足够小,以致于可以将其看成一个几何上没有维度的点;同时微观上足够大,它里面包含着许许多多的分子,其行为已经表现出大量分子的统计学性质。
一.连续介质模型§1.1 概述第一节流体静力学基本方程式静止:流体在重力和压力作用下达到平衡。
静止流体的规律:实际上是流体在重力作用下内部压力的变化规律。
一、流体的密度1.定义:单位体积流体所具有的质量。
ρ= m / V [ kg / m 3]获得方法:(1)查物性数据手册(附录2,3,5,6)(2)公式计算:2、影响ρ的主要因素:m pMV RTρ==()p t f ,=ρ液体:()t f =ρ——不可压缩流体气体:()p t f ,=ρ——可压缩流体3. 气体密度的计算压力不高时气体的密度可按理想气体方程进行计算:,wn wB wA x x x 、、、⋯总其中m m x iwi =假设混合后总体积不变,4、混合物的密度1)液体混合物的密度ρm (原则:混合前后总体积不变)取1kg 液体,令液体混合物中各组分的质量分率分别为:iwi m x kg m == 1时,当总mnwnwBwAm x x x V ρρρρ总总=+++=21nwnwBwAmx x x ρρρρ+++=∴211——液体混合物密度计算式2)气体混合物的密度(原则:混合前后总质量不变)取1m 3 的气体为基准,令各组分的体积分率为:x vA,x vB ,…,x Vn , 其中:混合物中各组分的质量为:Vn n VB VA x x x ρρρ,......,,21知,由Vm=ρiVi V x =当V 总=1m 3时,若混合前后, 气体的质量不变,总总V x x x m m n n ρρρρ=+++=.......2211当V 总=1m 3时,nn m x x x ρρρρ+++=......2211——气体混合物密度计算式ivi V x V =总在数值上:ρν1=1)比容:单位质量的流体所具有的体积,用υ表示,单位为m 3/kg 。






第一章流体静力学基本方程: )(2112z z g p p -+=ρ或ghp p ρ+=0双液位U 型压差计的指示::)21(21ρρ-=-Rg p p ) R 高度差 液封高度:h=p /ρg质量流量qm=ρqv ;流速:u=qv /A ;质量流速:ω= qm /A=ρu ;管路直径:d=连续性方程:常数=uA理想流体的伯努力方程:ρρ222212112121p u g z p u g z ++=++ 实际流体机械能衡算方程:f e h p u g z W p u g z ∑+++=+++ρρ222212112121不可压缩流体定态流动的柏努利方程式:––––能量衡算式牛顿粘性定律:dyduμτ= 雷诺数:μρdu =Re哈根-泊谡叶方程:232dlup f μ=∆ 范宁公式:ρρμλfp dlu u d l Wf ∆==⋅⋅=22322 摩擦阻力损失22u d l h f λ= 层流 Re64=λ非圆管当量直径 ∏=Ad e 4 局部阻力:2'2'22u h u d l h f e f ⋅=⋅⋅=ξλ或;流道突然扩大:2211⎪⎭⎫ ⎝⎛-=A A ξ;突然缩小:22115.0⎪⎭⎫ ⎝⎛-=A A ξ孔板流量计 ρP∆=200A C q V , g R i )(ρρ-=∆P第二章 扬程泵的有效功率 e V e H gq P ρ=泵效率 aeP P =η流体输送机械的效率:NN e=η管路特性曲线:∑+=Hf H H e ,其中gpz H ρ∆+∆=,g u d l l H e f 2))((2ξλ∑++∑=∑ 离心泵的汽蚀余量:gp g u g p NPSH vρρ-+=2211 离心泵的允许安装高度:10,0)(----=f r vg H NPSH gp p H ρ,10,212'---=f s g H g u H H 最大允许安装高度 100][-∑--=f Vg H gp g p H ρρ]5.0)[(+-r NPSH第三章层流区重力沉降速度:()μρρ182gd u s t -=斯托克斯沉降公式 μρρ18)(2gd u p p t -=, 2Re <p过滤速率基本方程 )(22e V V KA d dV +=τ , 其中 φμ012r K S -∆=P 恒速过滤 τ222KA VV V e =+ 恒压过滤 τ222KA VV V e =+第四章傅立叶定律:n t dAdQ ϑϑλ-=,dx dt A Q λ-=热导率与温度的线性关系:)1(0t αλλ+= 单层壁的定态热导率:bt t AQ 21-=λ,或mA b tQ λ∆=单层圆筒壁的定态热传导方程: )ln1(21221r r t t l Q λπ-=或m A b t t Q λ21-=牛顿冷却定律:)(t t A Q w -=α,)(T T A Q w -=α流体在圆管内强制对流传热:10000Re >,1600Pr 6.0<<,50/>d ln Nu Pr Re 023.08.0=,或nCp du d ⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=λμμρλα8.0023.0,其中当流体被加热时,n=0.4,当流体被冷却时n=0.3普朗克数 λμp C =Pr 努塞尔数 λαlNu =传热速率方程式 m t KA Q ∆= 2121ln t t t t t m ∆∆∆-∆=∆热量衡算式:无相变时: )()(21222111t t C q T T C q Q p m p m -=-= 或 若为饱和蒸气冷凝:)(12221t t c q r q Q p m m -==若冷凝液出口温度T2低于饱和温度Ts 。


流体流动知识点一、 流体静力学基本方程式或 注意:1、应用条件:静止的连通着的同一种连续的流体。
2、压强的表示方法: 绝压—大气压=表压 表压常由压强表来测量;大气压—绝压=真空度 真空度常由真空表来测量。
3、压强单位的换算:1atm=760mmHg=10.33mH 2O=101.33kPa=1.033kgf/cm2=1.033at4、应用:水平管路上两点间压强差与U 型管压差计读数R 的关系:处于同一水平面的液体,维持等压面的条件必须时静止、连续和同一种液体 二、定态流动系统的连续性方程式––––物料衡算式二、 定态流动的柏努利方程式––––能量衡算式以单位质量流体(1kg 流体)为基准的伯努利方程:讨论点:1、流体的流动满足连续性假设。
)(2112z z g p p -+=ρgh p p ρ+=0gRp p A )(21ρρ-=-常数常数=====≠ρρρρuA A u A u w s A ΛΛ222111,常数常数======uA A u A u V s A ΛΛ2211,ρ21221221///圆形管中流动,常数d d A A u u A ===ρf h u P gZ We u P gZ ∑+++=+++2222222111ρρ2、理想流体,无外功输入时,机械能守恒式:3、可压缩流体,当Δp/p 1<20%,仍可用上式,且ρ=ρm 。
4、注意运用柏努利方程式解题时的一般步骤,截面与基准面选取的原则。
5、流体密度ρ的计算:理想气体 ρ=PM/RT混合气体混合液体上式中:x vi ––––体积分率;x wi ––––质量分率。
6、gz 、u 2/2、p/ρ三项表示流体本身具有的能量,即位能、动能和静压能。
∑h f 为流经系统的能量损失。
We 为流体在两截面间所获得的有效功,是决定流体输送设备重要参数。
输送设备有效功率Ne=We·w s ,轴功率N=Ne/η(W )7、以单位重量流体为基准的伯努利方程, 各项的单位为m : [m] 22112212g 22f P u P u Z He Z H g g gρρ+++=+++ 以单位体积流体为基准的伯努利方程,各项的单位为Pa :[]22e f a f f u W gh p h p p h ρρρρρ∆=+∆++∑∆=∑而2222222111u P gZ u P gZ ++=++ρρvn n v v m x x x ρρρρ+++=Λ2211f e H gu g p Z H +∆+∆+∆=22ρnwn w m w m x x x ρρρρ+++=Λ22112212112222f u u gZ P We gZ P h ρρρρρρ+++=+++∑3、流型的比较:①质点的运动方式;②速度分布,层流:抛物线型,平均速度为最大速度的0.5倍;湍流:碰撞和混和使速度平均化。


第一章 流体流动与输送机械1. 流体静力学基本方程:gh p p ρ+=022. 双液位U 型压差计的指示: )21(21ρρ-=-Rg p p )3. 伯努力方程:ρρ222212112121p u g z p u g z ++=++4. 实际流体机械能衡算方程:f W p u g z p u g z ∑+++=++ρρ222212112121+ 5. 雷诺数:μρdu =Re6. 范宁公式:ρρμλfp dlu u d l Wf ∆==⋅⋅=22322 7. 哈根-泊谡叶方程:232d lup f μ=∆ 8. 局部阻力计算:流道突然扩大:2211⎪⎭⎫ ⎝⎛-=A A ξ流产突然缩小:⎪⎭⎫ ⎝⎛-=2115.0A A ξ第二章 非均相物系分离1. 恒压过滤方程:t KA V V V e 222=+令A V q /=,A Ve q e /=则此方程为:kt q q q e =+22第三章 传热1. 傅立叶定律:n t dAdQ ϑϑλ-=,dxdtA Q λ-= 2. 热导率与温度的线性关系:)1(0t αλλ+= 3. 单层壁的定态热导率:bt t AQ 21-=λ,或mA b tQ λ∆=4. 单层圆筒壁的定态热传导方程: )ln1(21221r r t t l Q λπ-=或m A b t t Q λ21-=5. 单层圆筒壁内的温度分布方程:C r l Qt +-=ln 2λπ(由公式4推导) 6. 三层圆筒壁定态热传导方程:34123212141ln 1ln 1ln 1(2r r r r r r t t l Q λλλπ++-=7. 牛顿冷却定律:)(t t A Q w -=α,)(T T A Q w -=α8. 努塞尔数λαl Nu =普朗克数λμCp =Pr 格拉晓夫数223μρβtl g Gr ∆= 9. 流体在圆形管内做强制对流:10000Re >,1600Pr 6.0<<,50/>d lk Nu Pr Re 023.08.0=,或kCp du d ⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=λμμρλα8.0023.0,其中当加热时,k=0.4,冷却时k=0.3 10. 热平衡方程:)()]([1222211t t c q T T c r q Q p m s p m -=-+=无相变时:)()(12222111t t c q T T c q Q p m p m -=-=,若为饱和蒸气冷凝:)(12221t t c q r q Q p m m -== 11. 总传热系数:21211111d d d d b K m ⋅+⋅+=αλα 12. 考虑热阻的总传热系数方程:212121211111d d R R d d d d b K s s m ⋅++⋅+⋅+=αλα 13. 总传热速率方程:t KA Q ∆=14. 两流体在换热器中逆流不发生相变的计算方程:⎪⎪⎭⎫⎝⎛-=--22111112211lnp m p m p m c q c q c q KA t T t T 15. 两流体在换热器中并流不发生相变的计算方程:⎪⎪⎭⎫ ⎝⎛+=--22111122111ln p m p m p m c q c q c q KA t T t T 16. 两流体在换热器中以饱和蒸气加热冷流体的计算方程:2221ln p m c q KAt T t T =--第四章 蒸发1.蒸发水量的计算:110)(Lx x W F Fx =-= 2.水的蒸发量:)1(1x x F W -=3. 完成时的溶液浓度:WF F x -=04.单位蒸气消耗量:rr D W '=,此时原料液由预热器加热至沸点后进料,且不计热损失,r 为加热时的蒸气汽化潜热r ’为二次蒸气的汽化潜热 5.传热面积:mt K QA ∆=,对加热室作热量衡算,求得Dr h H D Q c =-=)(,1t T t -=∆,T 为加热蒸气的温度,t 1为操作条件下的溶液沸点。
化工原理上册主要公式第一章 流体流动与输送机械 1. 流体静力学基本方程:gh p p ρ+=022. 双液位U 型压差计的指示: )(2121ρρ-=-Rg p p )3. 连续性方程:常数=uA4. 理想流体的伯努力方程:ρρ222212112121p u g z p u g z ++=++ 5. 实际流体机械能衡算方程:f e h p u g z W p u g z ∑+++=+++ρρ222212112121 6. 雷诺数:μρdu =Re7. 直管阻力:ρρμλff p d lu u d l h ∆==⋅⋅=223228. 局部阻力:2'2'22u h u d l h f e f ⋅=⋅⋅=ξλ或9. 出口局部阻力系数:1=ξ;进口的局部阻力系数:5.0=ξ 10. 流体输送机械的效率:NN e=η 11. 流体输送机械的轴功率:s e w W gQH N ==ρ12. 管路特性曲线:2e e BQ K H +=,其中gp z K ρ∆+∆=,gu d l l H BQ e f e2))((22ξλ∑++∑=∑=13. 单泵的特性曲线:2BQ A H -=,两台相同泵并联的特性曲线:22⎪⎭⎫⎝⎛-=Q B A H ,两台相同泵串联的特性曲线:22BQ A H-= 14. 离心泵的汽蚀余量:gp g u g p NPSH vρρ-+=2211 15. 离心泵的允许吸上真空度:gp p H a s ρ1'-=16. 离心泵的允许安装高度:10,0)(----=f r vg H NPSH gp p H ρ,10,212'---=f s g H gu H H17. 比例定律:32''''''⎪⎭⎫⎝⎛=⎪⎭⎫⎝⎛==n n N N n n H H n n Q Q ,18. 切割定律:32''''''⎪⎭⎫⎝⎛=⎪⎭⎫⎝⎛==D D N N D D H H D D Q Q ,第二章 非均相物系分离 1. 形状系数:ps S S =φ 2. 层流区重力沉降速度:()μρρ182gd u s t -=3. 降尘室颗粒完全除去的条件:t θθ≥或t u H u l //≥4. 降尘室的生产能力:t s u A V 底≤5. 层流区离心沉降速度:()Ru d u Ts r 2218μρρ-=6. 旋风分离器能分离下来的临界颗粒的粒径:i c u B d /∝7. 总效率和粒级效率的关系:∑==ni i p i x 1,0ηη8. 恒压过滤方程:θ222KA V V V e =+,e e KA V θ22=,)()(22e e KA V V θθ+=+ 9. 连续过滤机的浸没度:360浸没角度=ψ10. 当滤布阻力忽略时,连续过滤机的生产能力:ψKn A Q 465= 第三章 传热1. 单层壁的定态热导率:,或mS b tQ λ∆=2. 多层圆筒壁定态热传导方程:∑=+-=ni mii in S b t t Q 111λ 3. 牛顿冷却定律:t S Q ∆=α 4. 总传热速率方程:m o o t S K Q ∆=5. 热负荷:流体无相变时,热流体放出的热量:)(21T T c W Q ph h -=,冷流体吸收的热量:)(12t t c W Q pc c -= 流体只有相变时的热负荷:Wr Q =6. 考虑热阻的总传热系数方程:io si so i o i m o o d d R R d d d d b K ⋅++⋅+⋅+=αλα111o 7. 逆流和并流时对数平均温度差:1212ln t t t t t m ∆∆∆-∆=∆ 8. 错流和折流时的温度差:'m t m t t ∆=∆∆φ9. 若热流体是最小值流体:mph h pc c ph h t T T C W KSNTU T T t t C W C W C C t T T T ∆-==--==--=21min 2112max min 1121,,ε 10. 若冷流体是最小值流体:mpc c ph h pc c t t t C W KSNTU t t T T C W C W C C t T t t ∆-==--==--=12min 1221max min 1112,,ε 11. 努塞尔数λαl Nu =普朗克数λμCp =Pr 12. 流体在圆形管内做强制对流:10000Re>,1600Pr6.0<<,50/>dlnNu PrRe023.08.0=,或nCpdud⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛=λμμρλα8.0023.0,其中当流体被加热时,n=0.4,当流体被冷却时n=0.3。
第一章 流体流动与输送机械1. 流体静力学基本方程:gh p p ρ+=022. 双液位U 型压差计的指示: )21(21ρρ-=-Rg p p )3. 伯努力方程:ρρ222212112121p u g z p u g z ++=++4. 实际流体机械能衡算方程:f W p u g z p u g z ∑+++=++ρρ222212112121+ 5. 雷诺数:μρdu =Re6. 范宁公式:ρρμλfp d lu u d l Wf ∆==⋅⋅=22322 7. 哈根-泊谡叶方程:232d lup f μ=∆ 8. 局部阻力计算:流道突然扩大:2211⎪⎭⎫ ⎝⎛-=A A ξ流产突然缩小:⎪⎭⎫ ⎝⎛-=2115.0A A ξ第二章 非均相物系分离1. 恒压过滤方程:t KA V V V e 222=+令A V q /=,A Ve q e /=则此方程为:kt q q q e =+22第三章 传热1. 傅立叶定律:n t dAdQ ϑϑλ-=,dxdt A Q λ-= 2. 热导率与温度的线性关系:)1(0t αλλ+= 3. 单层壁的定态热导率:bt t AQ 21-=λ,或mA b tQ λ∆=4. 单层圆筒壁的定态热传导方程: )ln1(21221r r t t l Q λπ-=或m A b tt Q λ21-=5. 单层圆筒壁内的温度分布方程:C r l Qt +-=ln 2λπ(由公式4推导)6. 三层圆筒壁定态热传导方程:34123212141ln 1ln 1ln 1(2r r r r r r t t l Q λλλπ++-=7. 牛顿冷却定律:)(t t A Q w -=α,)(T T A Q w -=α8. 努塞尔数λαl Nu =普朗克数λμCp =Pr 格拉晓夫数223μρβtl g Gr ∆= 9. 流体在圆形管内做强制对流:10000Re >,1600Pr 6.0<<,50/>d lk Nu Pr Re 023.08.0=,或kCp du d ⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=λμμρλα8.0023.0,其中当加热时,k=,冷却时k= 10. 热平衡方程:)()]([1222211t t c q T T c r q Q p m s p m -=-+=无相变时:)()(12222111t t c q T T c q Q p m p m -=-=,若为饱和蒸气冷凝:)(12221t t c q r q Q p m m -== 11. 总传热系数:21211111d d d d b K m ⋅+⋅+=αλα 12. 考虑热阻的总传热系数方程:212121211111d d R R d d d d b K s s m ⋅++⋅+⋅+=αλα 13. 总传热速率方程:t KA Q ∆=14. 两流体在换热器中逆流不发生相变的计算方程:⎪⎪⎭⎫⎝⎛-=--22111112211lnp m p m p m c q c q c q KA t T t T 15. 两流体在换热器中并流不发生相变的计算方程:⎪⎪⎭⎫ ⎝⎛+=--22111122111lnp m p m p m c q c q c q KA t T t T 16. 两流体在换热器中以饱和蒸气加热冷流体的计算方程:2221ln p m c q KAt T t T =--第四章 蒸发1. 蒸发水量的计算:110)(Lx x W F Fx =-=2. 水的蒸发量:)1(1x x F W -= 3. 完成时的溶液浓度:WF F x -=4. 单位蒸气消耗量:rr D W '=,此时原料液由预热器加热至沸点后进料,且不计热损失,r 为加热时的蒸气汽化潜热r ’为二次蒸气的汽化潜热 5. 传热面积:mt K QA ∆=,对加热室作热量衡算,求得Dr h H D Q c =-=)(,1t T t -=∆,T 为加热蒸气的温度,t 1为操作条件下的溶液沸点。