2015高考理科数学新课标Ⅱ精校版

2015年高考全国新课标卷Ⅱ理科数学真题(青海;西藏;甘肃;贵州;内蒙古;新疆;宁夏;吉林;黑龙江;云南;辽宁;广西;海南)一、选择题1.已知集合A={-2,-1,0,1,2}，B={X|（X-1）（X+2）<0}，则AB=（ ） A ．{-1,0} B ．{0,1} C ．{-1,0,1} D ．{0,1,2}2.若a 为实数，且（2+ai ）（a-2i ）= - 4i ，则a=（ ）A ．-1B ．0C ．1D ．23.根据下面给出的2004年至2013年我国二氧化硫排放量（单位：万吨）柱形图，以下结论中不正确的是（ ）A ．逐年比较，2008年减少二氧化硫排放量的效果最显著B ．2007年我国治理二氧化硫排放显现成效C ．2006年以来我国二氧化硫排放量呈减少趋势D ．2006年以来我国二氧化硫排放量与年份正相关4.已知等比数列{a n } 满足a 1=3，a 1+a 3+a 5=21，则a 3+a 5+a 7=（ ）A ．21B ．42C ．63D ．845.设函数f （x ）=f (x )={1+log 2,(2−x ),x <12x−1,x ≥1则f （-2）+f （log 212）=（ ）A ．3B ．6C ．9D ．12 6.一个正方体被一个平面截去一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为（ ）A ．18B ．17C ．16D ．157.过三点A （1,3），B （4,2），C （1，-7）的圆交y 轴于M ，N 两点，则IMNI=（ ）A ．2√6B ．8C ．4√6D ．108.下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”。

执行该程序框图，若输入的a , b 分别为14 ，18，则输出的a=（ ）A ．0B ．2C ．4D ．149.已知A,B 是球O 的球面上两点，∠AOB=90o ，C 为该球上的动点，若三棱锥O-ABC 的体积最大值为36，则球O 的表面积为（ ）A ．36πB ．64πC ．144πD ．256π10.如图，长方形ABCD 的边2AB =，1BC =，O 是AB 的中点，点P 沿着边BC ，CD 与DA 运动，记BOP x ∠=，将动点P 到,A B 两点距离之和表示为x 的函数，则()y f x =的图像大致为（ ）A ．B ．C ．D ．11.已知A ，B 为双曲线E 的左，右顶点，点M 在E 上，△ABM 为等腰三角形，且顶角为120°，则E 的离心率为（ ）A B ．2 C D 12.设函数f ’(x)是奇函数f(x)(x ∈R)的导函数，f(-1)=0，当x>0时，x f ’(x)- f(x)<0,则使得f(x)>0成立的x 的取值范围是（ ）A ．（−∞，-1）∪（0,1）B ．（−1，0）∪（1,+∞）C ．（−∞，-1）∪（-1,0）D ．（0，1）∪（1,+∞）二、填空题13.设向量a,b 不平行，向量λ a+b 与a+2b 平行，则实数 λ =14.若x ，y 满足约束条件，则z=x+y 的最大值为 15.4()(1)a x x ++的展开式中x 的奇数次幂项的系数之和为32，则a=16.设S n 是数列｛a n ｝的前n 项和，且1111,n n n a a s s ++=-=，则S n =三、解答题17.△ABC 中，D 是BC 上的点，AD 平分∠BAC ，△ABD 面积是△ADC 面积的2倍（I ）求Csin B sin ∠∠ （II ）若AD=1，DC=22，求BD 和AC 的长18.某公司为了了解用户对其产品的满意度，从A ，B 两地区分别随机抽查了20个用户，得到用户对产品的满意度评分如下：A 地区：62 73 81 92 95 85 74 64 53 7678 86 95 66 97 78 88 82 76 89B 地区：73 83 62 51 91 46 53 73 64 8293 48 65 81 74 56 54 76 65 79（1）根据两组数据完成两地区用户满意度评分的茎叶图，并通过茎叶图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，给出结论即可）（Ⅱ）根据用户满意度评分，将用户的满意度从低到高分为三个等级：记事件C ：“A 地区用户的满意等级高于B 地区用户的满意度等级”.假设两地区用户的评价结果互相独立。

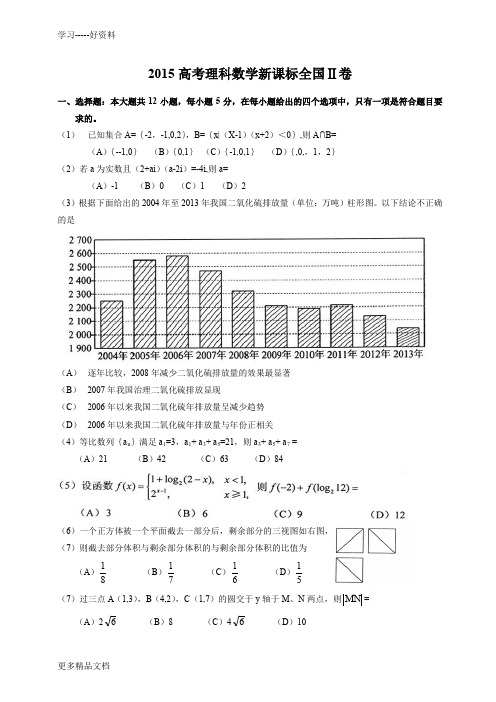
2015高考理科数学新课标全国Ⅱ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1） 已知集合A=｛-2，-1,0,2｝，B=｛x|（X-1）（x+2）＜0｝,则A∩B=（A ）｛--1,0｝ （B ）｛0,1｝ （C ）｛-1,0,1｝ （D ）｛,0,，1，2｝（2）若a 为实数且（2+ai ）（a-2i ）=-4i,则a=（A ）-1 （B ）0 （C ）1 （D ）2（3）根据下面给出的2004年至2013年我国二氧化硫排放量（单位：万吨）柱形图。

以下结论不正确的是（A ） 逐年比较，2008年减少二氧化硫排放量的效果最显著 （B ） 2007年我国治理二氧化硫排放显现（C ） 2006年以来我国二氧化硫年排放量呈减少趋势 （D ） 2006年以来我国二氧化硫年排放量与年份正相关 （4）等比数列｛a n ｝满足a 1=3，a 1+ a 3+ a 5=21，则a 3+ a 5+ a 7 =（A ）21 （B ）42 （C ）63 （D ）84（6）一个正方体被一个平面截去一部分后，剩余部分的三视图如右图， （7）则截去部分体积与剩余部分体积的与剩余部分体积的比值为（A ）81 （B ）71 （C ）61 （D ）51（7）过三点A （1,3），B （4,2），C （1,7）的圆交于y 轴于M 、N 两点，则MN =（A ）26 （B ）8 （C ）46 （D ）10（8）右边程序抗土的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”。

执行该程序框图，若输入a,b分别为14,18，则输出的a=A.0B.2C.4D.14（9）已知A,B是球O的球面上两点，∠AOB=90,C为该球面上的动点，若三棱锥O-ABC体积的最大值为36，则球O的表面积为A．36π B.64π C.144π D.256π10.如图，长方形ABCD的边AB=2，BC=1，O是AB的中点，点P沿着边BC，CD与DA运动，∠BOP=x。

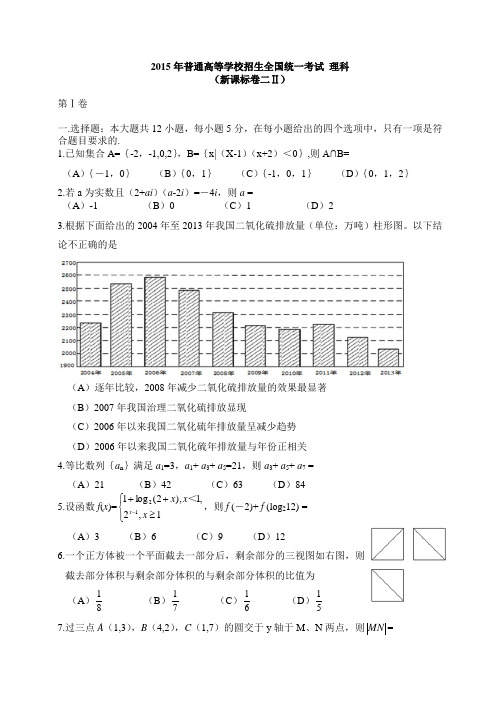
2015年普通高等学校招生全国统一考试 理科（新课标卷二Ⅱ）第Ⅰ卷一.选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合A=｛-2，-1,0,2｝，B=｛x|（X-1）（x+2）＜0｝,则A∩B= （A ）｛－1，0｝ （B ）｛0，1｝ （C ）｛-1，0，1｝ （D ）｛0，1，2｝2.若a 为实数且（2+ai ）（a -2i ）=－4i ，则a =（A ）-1 （B ）0 （C ）1 （D ）23.根据下面给出的2004年至2013年我国二氧化硫排放量（单位：万吨）柱形图。

以下结论不正确的是（A ）逐年比较，2008年减少二氧化硫排放量的效果最显著 （B ）2007年我国治理二氧化硫排放显现（C ）2006年以来我国二氧化硫年排放量呈减少趋势 （D ）2006年以来我国二氧化硫年排放量与年份正相关 4.等比数列｛a n ｝满足a 1=3，a 1+ a 3+ a 5=21，则a 3+ a 5+ a 7 = （A ）21 （B ）42 （C ）63 （D ）845.设函数f (x )=⎩⎨⎧≥++-1,2,1),2(log 112x x x x ＜，则f (－2)+ f (log 212) =（A ）3 （B ）6 （C ）9 （D ）126.一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则 截去部分体积与剩余部分体积的与剩余部分体积的比值为（A ）81 （B ）71 （C ）61（D ）517.过三点A （1,3），B （4,2），C （1,7）的圆交于y 轴于M 、N 两点，则MN =（A ）26 （B ）8 （C ）46 （D ）10 8.右边程序抗土的算法思路源于我国古代数学名著《九章算术》 中的“更相减损术”。

执行该程序框图，若输入a,b 分别为14,18， 则输出的a= （A ）0 （B ）2 （C ）4 （D ）149.已知A,B 是球O 的球面上两点，∠AOB=90,C 为该球面上的动点，若三棱锥O-ABC 体 积的最大值为36，则球O 的表面积为（A ）36π （B ）64π （C ）144π （D ）256π10.如图，长方形ABCD 的边AB=2，BC=1，O 是AB 的中点，点P 沿着边BC ，CD 与 DA 运动，∠BOP=x 。

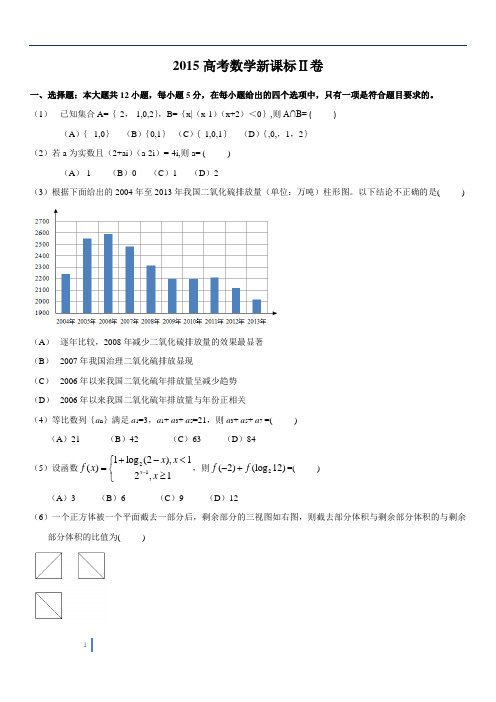
2015高考数学新课标Ⅱ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1） 已知集合A=｛-2，-1,0,2｝，B=｛x|（x-1）（x+2）＜0｝,则A∩B= ( )（A ）｛--1,0｝ （B ）｛0,1｝ （C ）｛-1,0,1｝ （D ）｛,0,，1，2｝（2）若a 为实数且（2+ai ）（a-2i ）=-4i,则a= ( )（A ）-1 （B ）0 （C ）1 （D ）2（3）根据下面给出的2004年至2013年我国二氧化硫排放量（单位：万吨）柱形图。

以下结论不正确的是( )（A ） 逐年比较，2008年减少二氧化硫排放量的效果最显著（B ） 2007年我国治理二氧化硫排放显现（C ） 2006年以来我国二氧化硫年排放量呈减少趋势（D ） 2006年以来我国二氧化硫年排放量与年份正相关（4）等比数列｛a n ｝满足a 1=3，a 1+ a 3+ a 5=21，则a 3+ a 5+ a 7 =( )（A ）21 （B ）42 （C ）63 （D ）84（5）设函数211log (2),1()2,1x x x f x x -+-<⎧=⎨≥⎩，则2(2)(log 12)f f -+=( ) （A ）3 （B ）6 （C ）9 （D ）12（6）一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的与剩余部分体积的比值为( )（A ）81 （B ）71 （C ）61 （D ）51 （7）过三点A （1,3），B （4,2），C （1,-7）的圆交于y 轴于M 、N 两点，则MN =( )（A ）26 （B ）8 （C ）46 （D ）10（8）右边程序抗土的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”。

执行该程序框图，若输入a,b 分别为14,18，则输出的a=( )A.0B.2C.4D.14（9）已知A,B 是球O 的球面上两点，∠AOB=90,C 为该球面上的动点，若三棱锥O-ABC 体积的最大值为36，则球O 的表面积为( )A ．36π B.64π C.144π D.256π（10）如图，长方形ABCD 的边AB=2，BC=1，O 是AB 的中点，点P 沿着边BC ，CD 与DA 运动，∠BOP=x 。

2015年高考数学试题（理） 第1页【共10页】2015年普通高等学校招生全国统一考试（新课标Ⅱ卷）理科数学第Ⅰ卷一、选择题：（本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的.）1．已知集合A ={-2，-1，0，2}，B ={x |(x -1)(x +2)<0}，则A ∩B =（ ）A ．{-1，0}B ．{0，1}C ．{-1，0，1}D ．{0，1，2}2．若a 为实数且(2+ai )(a -2i ) =-4i ，则a =（ ）A ．-1B ．0C ．1D ．23．根据下面给出的2004年至2013年我国二氧化硫年排放量（单位：万吨）柱形图，以下结论中不正确的是（ ）A ．逐年比较，2008年减少二氧化硫排放量的效果最显著.B ．2007年我国治理二氧化硫排放显现成效.C ．2006年以来我国二氧化硫年排放量呈减少趋势.D ．2006年以来我国二氧化硫年排放量与年份正相关.4．已知等比数列{a n }满足a 1=3，a 1+ a 3+ a 5=21，则a 3+ a 5+ a 7=（ ）A ．21B ．42C ．63D ．845．设函数211log (2)(1)()2(1)x x x f x x -+-<⎧=⎨≥⎩，则2(2)(log 12)f f -+=（ ） A ．3 B ．6 C ．9D ．12 6．一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为（ ）A ．81B ．71C ．61D ．51 7．过三点A (1,3)，B (4,2)，C (1,-7)的圆交于y 轴于M 、N 两点，则MN =（ ）2015年高考数学试题（理） 第2页【共10页】A．B ．8 C．D ．108．右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”. 执行该程序框图，若输入a ，b 分别为14，18，则输出的a =（ ）A ．0B ．2C ．4D ．149．已知A ，B 是球O 的球面上两点，∠AOB =90º，C 为该球面上的动点，若三棱锥O -ABC 体积的最大值为36，则球O 的表面积为（ ）A ．36πB ．64πC ．144πD ．256π10．如图，长方形ABCD 的边AB =2，BC =1，O 是AB 的中点，点P 沿着边BC ，CD 与DA 运动，记∠BOP =x.将动点P 到A ，B 两点距离之和表示为x 的函数f （x ），则f （x ）的图像大致为 （ ）A ．B ．C ．D ．11．已知A ，B 为双曲线E 的左，右顶点，点M 在E 上，∆ABM 为等腰三角形，且顶角为120°，则E 的离心率为（ ）AB ．2 CD12．设函数()f x '是奇函数()()f x x R ∈的导函数，(1)0f -=，当x >0时，()()0xf x f x '-<，则使得f (x ) >0成立的x 的取值范围是（ ）A ．(,1)(0,1)-∞-UB ．(1,0)(1,)-+∞UC ．(,1)(1,0)-∞--UD ．(0,1)(1,)+∞U第Ⅱ卷本卷包括必考题和选考题两部分.第13题～第21题为必考题，每个试题考生必须做答.第22题～第24题为选考题，考生根据要求做答.二、填空题：（本大题共4小题，每小题5分，共20分.）13．设向量a ，b 不平行，向量λ+a b 与2+a b 平行，则实数λ= ____________．2015年高考数学试题（理） 第3页【共10页】14．若x ，y 满足约束条件1020+220x y x y x y -+≥⎧⎪-≤⎨⎪-≤⎩，则z x y =+的最大值为____________．15．4()(1)a x x ++的展开式中x 的奇数次幂项的系数之和为32，则a =__________．16．设S n 是数列{a n }的前项和，且11a =-，11n n n a S S ++=，则S n =___________________．三、解答题：（解答应写出文字说明，证明过程或演算步骤.）17．（本小题12分）在∆ABC 中，D 是BC 上的点，AD 平分∠BAC ，∆ABD 面积是∆ADC 面积的2倍．（Ⅰ）求sin sin B C ∠∠；（Ⅱ）若AD =1，DCBD 和AC 的长． 18．（本小题12分）某公司为了解用户对其产品的满意度，从A ，B 两地区分别随机调查了20个用户，得到用户对产品的满意度评分如下：A 地区：62 73 81 92 95 85 74 64 53 7678 86 95 66 97 78 88 82 76 89B 地区：73 83 62 51 91 46 53 73 64 8293 48 65 81 74 56 54 76 65 79（Ⅰ）根据两组数据完成两地区用户满意度评分的茎叶图，并通过茎叶图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，得出结论即可）；（Ⅱ）根据用户满意度评分，将用户的满意度从低到高分为三个等级：区用户的评价结果相互独立，根据所给数据，以事件发生的频率作为相应事件发生的概率，求C 的概率．19．（本小题12分）如图，长方体ABCD -A 1B 1C 1D 1中AB =16，BC =10，AA 1=8，点E ，F 分别在A 1B 1，D 1C 1上，A 1E =D 1F =4，过点E ，F 的平面α与此长方体的面相交，交线围成一个正方形.（Ⅰ）在图中画出这个正方形（不必说出画法和理由）；（Ⅱ）求直线AF 与平面α所成角的正弦值.2015年高考数学试题（理） 第4页【共10页】20．（本小题12分）已知椭圆C ：2229x y m +=(m ＞0)，直线l 不过原点O 且不平行于坐标轴，l 与C 有两个交点A ，B ，线段AB 的中点为M .（Ⅰ）证明：直线OM 的斜率与l 的斜率的乘积为定值；（Ⅱ）若l 过点(,)3m m ，延长线段OM 与C 交于点P ，四边形OAPB 能否平行四边形？若能，求此时l 的斜率；若不能，说明理由．21．（本小题12分）设函数2()mx f x e x mx =+-.（Ⅰ）证明：f (x )在（-∞，0）单调递减，在（0，+∞）单调递增；（Ⅱ）若对于任意x 1,，x 2∈[-1，1]，都有｜f (x 1)-f (x 2)｜≤e -1，求m 的取值范围．请考生在第22、23、24题中任选择一题作答，如果多做，则按所做的第一题评分，做答时请用2B 铅笔在答题卡上将所选题目对应的题号方框涂黑.22．（本小题10分）【选修4-1：几何证明选讲】如图，O 为等腰三角形ABC 内一点，⊙O 与△ABC 的底边BC 交于M 、N 两点，与底边上的高AD 交于点G ，且与AB ，AC 分别相切于E ，F 两点.（Ⅰ）证明：EF ∥BC ；（Ⅱ）若AG 等于⊙O 的半径，且AE=MN=求四边形EBCF的面积.23．（本小题10分）【选修4-4：坐标系与参数方程】在直角坐标系xOy 中，曲线C 1：cos sin x t y t αα=⎧⎨=⎩（t 为参数，t ≠0）其中0απ≤<，在以O 为极点，x 轴正半轴为极轴的极坐标系中，曲线C 2:2sin ρθ=，C 3:ρθ=. （Ⅰ）求C 2与C 3交点的直角坐标；（Ⅱ）若C 1与C 2相交于点A ，C 1与C 3相交于点B ，求|AB |的最大值.24．（本小题10分）【选修4-5：不等式选讲】设a ，b ，c ，d 均为正数，且a b c d +=+，证明：（Ⅰ）若ab >cd>||||a b c d -<-的充要条件.2015年普通高等学校招生全国统一考试（新课标Ⅱ卷）理科数学【参考答案】一、选择题：1. 【答案】A解析：由已知得，故{1,0}A B =- ，故选A.{}21B x x =-<<2015年高考数学试题（理） 第5页【共10页】2. 【答案】B解析：由已知得4a + (a 2 -4)i = -4i ，所以4a = 0，a 2 -4 = -4，解得a = 0，故选B.3. 【答案】D解析：由柱形图可知，从2006年以来，我国二氧化硫排放量呈下降趋势，所以二氧化硫排放量与年份负相关，故选D.4. 【答案】B解析：设等比数列公比为q ，则a 1+a 1q 2+a 1q 4=21，又因为a 1=3，所以q 4+q 2-6=0，解得q 2=2，所以a 3+a 5+a 7=(a 1+a 3+a 5)q 2=42，故选B.5. 【答案】C解析：由已知得，又，所以，故．6. 【答案】D解析：由三视图得，在正方体ABCD -A 1B 1C 1D 1中，截去四面体A -A 1B 1D 1，如图所示，设正方体棱长为，则，故剩余几何体体积为，所以截去部分体积与剩余部分体积的比值为15，故选D. 7. 【答案】C解析：由已知得321143AB k -==--，27341CB k +==--，所以k AB k CB =-1，所以AB ⊥CB ，即△ABC 为直角三角形，其外接圆圆心为(1, -2)，半径为5，所以外接圆方程为(x -1)2+(y +2)2=25，令x =0，得2y =±，所以||MN = C.8. 【答案】B解析：程序在执行过程中，a ，b 的值依次为a =14，b =18，b =4，a =10，a =6，a =2，b =2，此时a =b =2程序结束，输出a 的值为2，故选B ．9. 【答案】C解析：如图所示，当点C 位于垂直于面的直径端点时，三棱锥的体积最大，设球O 的半径为R ，此时，故R=6，则球O 的表面积为，故选C ．10. 【答案】B2(2)1log 43f -=+=2log 121>22log 121log 62(log 12)226f -===2(2)(log 12)9f f -+=a 11133111326A A B D V a a -=⨯=3331566a a a -=AOB O ABC -2311136326O ABC C AOB V V R R R --==⨯⨯==24144S R ππ==12015年高考数学试题（理） 第6页【共10页】解析：由已知得，当点P 在BC 边上运动时，即04x π≤≤时，tan PA PB x +；当点P 在CD 边上运动时，即344x ππ≤≤，2x π≠时，PA PB +=当2x π=时，PA PB +=当点P 在AD 边上运动时，即34x ππ≤≤时，PA PB +=tan x ，从点P 的运动过程可以看出，轨迹关于直线2x π=对称，且，且轨迹非线型，故选B ． 11. 【答案】D 解析：设双曲线方程为22221(0,0)x y a b a b-=>>，如图所示，|AB |=|BM |，∠ABM =120º，过点M 作MN ⊥x 轴，垂足为N ，在Rt △BMN 中，|BN |=a，||MN =，故点M的坐标为(2)M a ，代入双曲线方程得a 2=b 2=c 2-a 2，即c 2=2a 2，所以e = D.12. 【答案】A解析：记函数()()f x g x x =，则2()()()x f x f x g x x '-'=，因为当x >0时，xf ´(x )-f (x )<0，故当x >0时，g ´ (x )<0，所以g (x )在(0, +∞)单调递减；又因为函数f (x )(x ∈R )是奇函数，故函数g (x )是偶函数，所以g (x )在(-∞, 0)单调递增，且g (-1)=g (1)=0．当0<x <1时，g (x )>0，则f (x )>0；当x <-1时，g (x )<0，则f (x )>0，综上所述，使得f (x )>0成立的x 的取值范围是(-∞, -1)∪(0, 1)，故选A ．二、填空题：13. 【答案】 解析：因为向量a b λ+ 与2a b + 平行，所以(2)a b k a b λ+=+ ，则12k kλ=⎧⎨=⎩，所以12λ=． 14. 【答案】 解析：画出可行域，如图所示，将目标函数变形为y =-x +z ，当z 取到最大时，直线y =-x +z 的纵截距最大，故将直线()()42f f ππ>12322015年高考数学试题（理） 第7页【共10页】 尽可能地向上平移到1(1,)2D ，则z =x +y 的最大值为32. 15. 【答案】解析：由已知得，故的展开式中x 的奇数次幂项分别为，，，，，其系数之和为，解得．16. 【答案】 解析：由已知得，两边同时除以，得，故数列是以为首项，为公差的等差数列，则，所以． 三、解答题： 17．解析：（Ⅰ）1sin 2ABD S AB AD BAD ∆=⋅∠，1sin 2ADC S AC AD CAD ∆=⋅∠，因为2A B D A D C S S ∆∆=，BAD CAD ∠=∠，所以2AB AC =，由正弦定理可得sin 1sin 2B AC C AB ∠==∠. （Ⅱ）因为::2ABD ADC S S BD DC ∆∆==，DC =所以BD =在ABD ∆和ADC ∆中，由余弦定理知，2222cos AB AD BD AD BD ADB =+-⋅∠，2222cos AC AD DC AD DC ADC =+-⋅∠，故222222326AB AC AD BD DC +=++=，由（Ⅰ）知2AB AC =，所以1AC =.18．解析：（Ⅰ）两地区用户满意度评分的茎叶图如下:B 地区用户满意度评分的平均值；A 地区用户满意度评分比较集中，B 地区用户满意度评分比较分散。

2015年普通高等学校招生全国统一考试理科数学（课标全国Ⅱ）第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．(2015课标全国Ⅱ，理1)已知集合A ＝{-2,-10,1,2}，B ＝{x |(x －1)(x ＋2)<0}，则A ∩B ＝( )．A ．{-1,0}B ．{0,1}C ．{-1,0,1}D ．{0,1,2}2．(2015课标全国Ⅱ，理2)若a 为实数，且(2＋a i)( a －2i)＝-4i ，则a ＝( )．A ．-1B ．0C ．1D ．23．(2015课标全国Ⅱ，理3)根据下面给出的2004年至2013年我国二氧化硫年排放量（单位：万吨）柱形图，以下结论中不正确的是A ．逐年比较，2008年减少二氧化硫排放量的效果最显著B ．2007年我国治理二氧化硫排放显现成效C ．2006年以来我国二氧化硫排放量呈减少趋势D ．2006年以来我国二氧化硫排放量与年份正相关4．(2015课标全国Ⅱ，理4)已知等比数列{a n }满足a 1＝3，a 1＋a 3＋a 5＝21，则a 3＋a 5＋a 7＝( )．A ．21B ．42C ．63D ．845．(2015课标全国Ⅱ，理5)函数f (x )＝ 1+log 2 2−x ,x <12x−1 ,x ≥1则f −2 +f log 212 = A ．3 B ．6 C ．9 D ．126．(2015课标全国Ⅱ，理6)一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为A ．18B ．17C ．16D ． 157．(2015课标全国Ⅱ，理7)过三点A(1,3)，B(4,2)，C(1,-7)，的圆交y 轴于M ，N 两点，则|MN|=A ．2 6B ．8C ．4 6D ．108．(2015课标全国Ⅱ，理8)右边程序框图的算法思想源于我国古代数学名著《九章算术》中的“更相减损术”。

2015年普通高等学校招生全国统一考试理 科 数 学一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1） 已知集合A=｛-2，-1,0，1,2｝，B=｛x|（x-1）（x+2）＜0｝,则A∩B=（ ）（A ）｛-1,0｝ （B ）｛0,1｝ （C ）｛-1,0,1｝ （D ）｛0,1,2｝（2）若a 为实数且（2+ai ）（a-2i ）=-4i,则a=（ ）（A ）-1 （B ）0 （C ）1 （D ）2（3）根据下面给出的2004年至2013年我国二氧化硫排放量（单位：万吨）柱形图。

以下结论不正确的是( )（A ） 逐年比较，2008年减少二氧化硫排放量的效果最显著 （B ） 2007年我国治理二氧化硫排放显现（C ） 2006年以来我国二氧化硫年排放量呈减少趋势 （D ） 2006年以来我国二氧化硫年排放量与年份正相关（4）等比数列｛a n ｝满足a 1=3，135a a a ++ =21，则357a a a ++= ( )（A ）21 （B ）42 （C ）63 （D ）84 （5）设函数211log (2),1,()2,1,x x x f x x -+-<⎧=⎨≥⎩,2(2)(log 12)f f -+=( )（A ）3 （B ）6 （C ）9 （D ）12（6）一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为（A ）81 （B ）71 （C ）61 （D ）51 （7）过三点A （1,3），B （4,2），C （1,-7）的圆交于y 轴于M 、N 两点，则MN =（A ）26 （B ）8 （C ）46 （D ）10（8）右边程序抗土的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”。

执行该程序框图，若输入a,b 分别为14,18，则输出的a=A.0B.2C.4D.14 （9）已知A,B 是球O 的球面上两点，∠AOB=90,C 为该球面上的动点，若三棱锥O-ABC 体积的最大值为36，则球O 的表面积为A ．36π B.64π C.144π D.256π10.如图，长方形ABCD 的边AB=2，BC=1，O 是AB 的中点，点P 沿着边BC ，CD 与DA 运动，记∠BOP=x ．将动点P 到A 、B 两点距离之和表示为x 的函数f （x ），则f （x ）的图像大致为（11）已知A ，B 为双曲线E 的左，右顶点，点M 在E 上，∆ABM为等腰三角形，且顶角为120°，则E 的离心率为（A（B ）2 （C（D（12）设函数f’(x)是奇函数()()f x x R ∈的导函数，f （-1）=0，当0x >时，'()()0xf x f x -<，则使得()0f x >成立的x 的取值范围是A ．(,1)(0,1)-∞-UB ．(1,0)(1,)-+∞UC ．(,1)(1,0)-∞--UD ．(0,1)(1,)+∞U二、填空题（13）设向量a r ，b r 不平行，向量a b λ+r r 与2a b +r r平行，则实数λ=_________． （14）若x ，y 满足约束条件1020,220,x y x y x y -+≥⎧⎪-≤⎨⎪+-≤⎩，，则z x y =+的最大值为____________．（15）4()(1)a x x ++的展开式中x 的奇数次幂项的系数之和为32，则a =__________． （16）设n S 是数列{}n a 的前n 项和，且11a =-，11n n n a S S ++=，则n S =________． 三．解答题（17）∆ABC 中，D 是BC 上的点，AD 平分∠BAC ，∆ABD 是∆ADC 面积的2倍。

2015年普通高等学校招生全国统一考试(全国新课标卷2)理科数学答案解析第Ⅰ卷一、选择题 1.【答案】A【解析】由已知得{|21}B x x =-<<，故,}10{AB -=，故选A ．【提示】解一元二次不等式，求出集合B ，然后进行交集的运算即可． 【考点】集合的交集运算和一元二次方程求根． 2.【答案】B【解析】由已知得24+(4)i 4i a -=-，所以40a =，244a -=-，解得0a =，故选B ．【提示】首先将坐标展开，然后利用复数相等解之． 【考点】复数的四则运算． 3.【答案】D【解析】解：A ．从图中明显看出2008年二氧化硫排放量比2007年的二氧化硫排放量明显减少，且减少的最多，故A 正确；B ．2004~2006年二氧化硫排放量越来越多，从2007年开始二氧化硫排放量变少，故B 正确；C ．从图中看出，2006年以来我国二氧化硫年排放量越来越少，故C 正确；D ．2006年以来我国二氧化硫年排放量越来越少，而不是与年份正相关，故D 错误． 故选：D【提示】A ．从图中明显看出2008年二氧化硫排放量比2007年的二氧化硫排放量减少的最多，故A 正确； B ．从2007年开始二氧化硫排放量变少，故B 正确；C ．从图中看出，2006年以来我国二氧化硫年排放量越来越少，故C 正确；D ．2006年以来我国二氧化硫年排放量越来越少，与年份负相关，故D 错误． 【考点】柱形图信息的获得． 4.【答案】B【解析】设等比数列公比为q ，则24111++21a a q a q =，又因为13a =，所以42+60q q -=，解得22q =，所以2357135++(++)42a a a a a a q ==，故选B ．【提示】由已知，13a =，135++21a a a =，利用等比数列的通项公式可求q ，然后在代入等比数列通项公式53261)(0,1)，故选())f x x=为减函数，,0)(0,+)∞上的偶函数，根据函数0等价于x g【解析】（Ⅰ）两地区用户满意度评分的茎叶图如下：122B A C C ，12212))+()B A A B C C P C 1，2A C ，C 108【解析】（Ⅰ）交线围成的正方形EHGF 如图：uuu r 即可求出法向量n，AF。

一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合21,01,2A =--｛，，｝，{}(1)(20B x x x =-+<,则A B =（ ）A ．{}1,0A =-B ．{}0,1C ．{}1,0,1-D ．{}0,1,2 【答案】A考点：集合的运算．2．若a 为实数且(2)(2)4ai a i i +-=-，则a =（ ） A ．1- B ．0 C ．1 D ．2 【答案】B 【解析】试题分析：由已知得24(4)4a a i i +-=-，所以240,44a a =-=-，解得0a =，故选B ． 考点：复数的运算．3．根据下面给出的2004年至2013年我国二氧化硫排放量（单位：万吨）柱形图。

以下结论不正确的是( )A ．逐年比较，2008年减少二氧化硫排放量的效果最显著B ．2007年我国治理二氧化硫排放显现2004年 2005年 2006年 2007年 2008年 2009年 2010年 2011年 2012年 2013年C ．2006年以来我国二氧化硫年排放量呈减少趋势D ．2006年以来我国二氧化硫年排放量与年份正相关 【答案】D 【解析】试题分析：由柱形图得，从2006年以来，我国二氧化硫排放量呈下降趋势，故年排放量与年份负相关，故选D ． 考点：正、负相关．4．等比数列｛a n ｝满足a 1=3，135a a a ++ =21，则357a a a ++= ( )A ．21B ．42C ．63D ．84 【答案】B考点：等比数列通项公式和性质． 5．设函数211log (2),1,()2,1,x x x f x x -+-<⎧=⎨≥⎩,2(2)(log 12)f f -+=( )A ．3B ．6C ．9D ．12 【答案】C 【解析】试题分析：由已知得2(2)1log 43f -=+=，又2log 121>，所以22log 121log 62(log 12)226f -===，故2(2)(log 12)9f f -+=，故选C ．考点：分段函数．6．一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为( ) A ．81 B ．71 C ．61 D ．51【答案】D 【解析】试题分析：由三视图得，在正方体1111ABCD A B C D -中，截去四面体111A A B D -，如图所示，，设正方体棱长为a ，则11133111326A AB D V a a -=⨯=，故剩余几何体体积为3331566a a a -=，所以截去部分体积与剩余部分体积的比值为51，故选D ．考点：三视图．CBADD 1C 1B 1A 17．过三点(1,3)A ，(4,2)B ，(1,7)C -的圆交y 轴于M ，N 两点，则||MN =( ) A ．26 B ．8 C ．46 D ．10 【答案】C【解析】由已知得321143AB k -==--，27341CB k +==--，所以1AB CB k k =-，所以AB CB ⊥，即ABC ∆为直角三角形，其外接圆圆心为(1,2)-，半径为5，所以外接圆方程为22(1)(2)25x y -++=，令0x =，得2y =±，所以MN =，故选C ．考点：圆的方程．8．右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入,a b 分别为14,18，则输出的a =( )A ．0B ．2C ．4D ．14 【答案】B 【解析】 试题分析：程序在执行过程中，a ，b 的值依次为14a =，18b =；4b =；10a =；6a =；2a =；2b =，此时2a b ==程序结束，输出a 的值为2，故选B ． 考点：程序框图．9．已知A,B 是球O 的球面上两点，∠AOB=90,C 为该球面上的动点，若三棱锥O-ABC 体积的最大值为36，则球O 的表面积为( ) A ．36π B.64π C.144π D.256π 【答案】C 【解析】试题分析：如图所示，当点C 位于垂直于面AOB 的直径端点时，三棱锥O ABC -的体积最大，设球O 的半径为R ，此时2311136326O ABC C AOB V V R R R --==⨯⨯==，故6R =，则球O 的表面积为24144S R ππ==，故选C ． 考点：外接球表面积和椎体的体积．BOAC10．如图，长方形ABCD 的边2AB =，1BC =，O 是AB 的中点，点P 沿着边BC ，CD 与DA 运动，记BOP x ∠=．将动P 到A 、B 两点距离之和表示为x 的函数()f x ，则()y f x =的图像大致为（ ）【答案】B 【解析】考点：函数的图象和性质． 11．已知A ，B 为双曲线E 的左，右顶点，点M 在E 上，∆ABM 为等腰三角形，且顶角为120°，则E 的离心率为（ ）AB ．2 CD【答案】D 【解析】DPCx试题分析：设双曲线方程为22221(0,0)x y a b a b-=>>，如图所示，AB BM =，0120ABM ∠=，过点M 作MN x ⊥轴，垂足为N ，在Rt BMN ∆中，BN a =，，故点M 的坐标为(2)M a ，代入双曲线方程得2222a b a c ==-，即222c a =，所以e =，故选D ．考点：双曲线的标准方程和简单几何性质．12．设函数'()f x 是奇函数()()f x x R ∈的导函数，(1)0f -=，当0x >时，'()()0xf x f x -<，则使得()0f x >成立的x 的取值范围是（ ）A ．(,1)(0,1)-∞-B ．(1,0)(1,)-+∞C ．(,1)(1,0)-∞--D ．(0,1)(1,)+∞【答案】A 【解析】试题分析：记函数()()f x g x x=，则''2()()()xf x f x g x x -=，因为当0x >时，'()()0xf x f x -<，故当0x >时，'()0g x <，所以()g x 在(0,)+∞单调递减；又因为函数()()f x x R ∈是奇函数，故函数()g x 是偶函数，所以()g x 在(,0)-∞单调递减，且(1)(1)0g g -==．当01x <<时，()0g x >，则()0f x >；当1x <-时，()0g x <，则()0f x >，综上所述，使得()0f x >成立的x 的取值范围是(,1)(0,1)-∞-，故选A ．考点：导数的应用、函数的图象与性质．第II 卷（非选择题，共90分）本卷包括必考题和选考题两部分。