人教版八年级数学下册学案第十八章复习

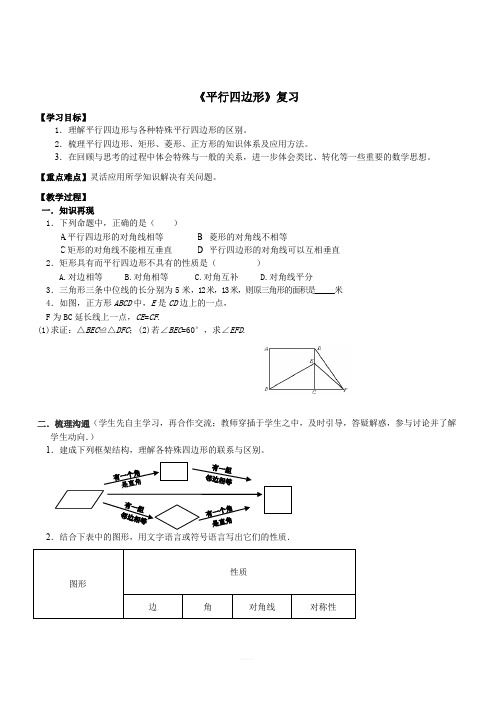
《平行四边形》复习【学习目标】1．理解平行四边形与各种特殊平行四边形的区别。

2．梳理平行四边形、矩形、菱形、正方形的知识体系及应用方法。

3．在回顾与思考的过程中体会特殊与一般的关系，进一步体会类比、转化等一些重要的数学思想。

【重点难点】灵活应用所学知识解决有关问题。

【教学过程】 一．知识再现2．矩形具有而平行四边形不具有的性质是（ ）A.对边相等B.对角相等C.对角互补D.对角线平分 3．三角形三条中位线的长分别为5米，12米，13米，则原三角形的面积是_____米 4．如图，正方形ABCD 中，E 是CD 边上的一点， F 为BC 延长线上一点，CE =CF .(1)求证：△BEC ≌△DFC ；(2)若∠BEC =60°，求∠EFD .二．梳理沟通（学生先自主学习，再合作交流；教师穿插于学生之中，及时引导，答疑解惑，参与讨论并了解学生动向．）1．建成下列框架结构，理解各特殊四边形的联系与区别。

2．结合下表中的图形，用文字语言或符号语言写出它们的性质．3．学会判定方法（让学生用符号语言再以文字语言对照比较）（通过活动，让学生明白结构，熟悉图形语言、文字语言、符号语言的互相翻译与应用。

）由教师演示课件，师生共述，加深理解本章的知识脉络。

）三．知识运用，拓展与创新（教师引导学生深度加工，习得悟得）例题1:已知，在四边形ABCD中，AB=CD,AD=BC,点F,E分别在BC和AD边上，AE=CF,EF和对角线AD交于点O，求证：点O是BD的中点。

例题2、已知如图：在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,求证：四边形EFGH是平行四边形.AD变式一：顺次链接矩形各边的中点得到的四边形是菱形。

变式二：顺次链接菱形各边的中点得到的四边形是矩形。

变式三：顺次链接正方形各边的中点得到的四边形是正方形。

变式四：顺次链接等腰梯形各边的中点得到的四边形是菱形。

变式五：若AC=BD,AC ┻BD,则四边形EFGH 是正方形。

1 / 2
新人教版八年级数学下册第十八章《矩形、菱形、正方形复习》导学案
教学时间：
学习目标：回顾平行四边形、矩形、菱形、正方形的定义、性质、判定
学习重点难点：平行四边形、矩形、菱形、正方形的定义、性质、判定的综合应用 学习过程：
一、自学指导
1.自学复习平行四边形、矩形、菱形、正方形的定义、性质、判定
2.平行四边形、矩形、菱形、正方形之间的关系：
二、自学检测：
1.如图，在矩形ABCD 中，CE ⊥BD ，E 为垂足，∠DCE ：∠ECB ＝3：1。

求∠ACE 的度数。

2.已知：如图，菱形ABCD 的周长为8cm ，∠ABC ：∠BAD=1：2，对角线AC 、BD 相交于点O ，求AC 的长及菱形的面积。

三、课堂练习：
3.如图，在矩形ABCD 中，点E 在AD 上，EC 平分∠BED 。

（1）△BEC 是否为等腰三角形？为什么？（2）若AB=1，∠ABE=45°，求BC 的长
O D C B A E E D C
B A
4.如图，在四边形ABCD中，AD∥BC，对角线AC的垂直平分线与边AD、BC分别相交于点E、F。

四边形AFCE是菱形吗？为什么？
四、课后作业
5、已知：如图，△ABC中，∠ACB=90°，CD是高，AE是角平分线，交CD于点F，
EG⊥AB，G为垂足。

试说明四边形CEGF是菱形。

教师的职务是‘千教万教，教人求真’;学生的职务是‘千学万学，学做真人’。

我们发现了儿童有创造力，认识了儿童有创造力，就须进一步把儿童的创造力解放出来。

——好词好句
2 / 2。

1、用15分钟左右的时间，独立完成“知识导图”和“知识梳理”的内容。

2独立、限时完成本节导学案，记录下疑惑的地方上课与同学讨论。

【知识梳理】几种特殊四边形的常用判定方法四边形 判定方法平行四边形矩形菱形正方形等腰梯形【预习案】1.下列说法中，不正确的是（ ）A ．既是矩形，又是菱形的四边形是正方形B ．正方形是对角线相等的菱形C ．正方形是对角线互相垂直的矩形D ．正方形是对角线互相平分的平行四边形2.如图EF 过矩形ABCD 对角线的交点O ，且分别交AB 、CD 于E 、F ，那么阴影部分的面积是矩形ABCD 的面积的（ ） （A ）51 （B ）41 （C ）31 （D ）1033.四边形ABCD 中，∠A ，∠B ，∠C ，∠D 的度数比是1：2：2：3，则这个四边形是4.如图，D ，E ，F 分别是△ABC 的边BC ，CA ， AB 上的点，且DE∥AB，DF∥CA ， 要使四边形AFDE 是菱形，则要增加的条件是________．（只写出符合要求的一个即可）【探究案】例1：已知：如图，□ABCD 中，E 、F 分别是AB 、CD 上的点，AE CF ，M 、N 分别是DE 、BF 的中点。

求证：四边形ENFM 是平行四边形。

例2：如图，在矩形ABCD 中，F 是BC 边上的一点，AF 的延长线交DC 的延长线于G ，DE ⊥AG 于E ，且DE ＝DC ，根据上述条件，请你在图中找出一对全等三角形，并证明你的结论。

例3：如图所示，DF 是□ABCD 中∠ADC 的平分线，EF∥AD 交DC 于点E ．（1）四边形AFED 是菱形吗？请说明理由； （2）如果∠A=60°，AD=5，求四边形AFED 的面积．例4：如图所示，在□ABCD 中，延长DC 到点E ，使BE=BC ；四边形ABED 是否为等腰梯形，请说明理由；例5：已知点D ，E ，F 分别是等腰△ABC 的边AB ，BC ，CA 的中点，且AB=AC 连结DE ，EF ，•要使四边形ADEF 是正方形，还需要添加条件_______ ，并说明理由课题 第18章平行四边形复习姓名班级小组评价学习目标:1.熟练掌握特殊四边形的判定方法，并能灵活运用解决一些简单的问题，提高逻辑推理能力；2.通过小组讨论，探究，结合具体题目的训练，体验特殊四边形有关知识的联系和区别.3．培养合作探究的能力，养成科学严谨的数学思维习惯.教学重点：平行四边形、矩形、菱形、等腰梯形的判定方法的应用教学难点：灵活应用特殊四边形判定方法解决问题 学法指导F B ED C A N M F ED C BAFABCDE当堂检测：1．矩形四条内角平分线能围成一个（）A．平行四边形 B．矩形 C．菱形 D．正方形2.如图，平行四边形ABCD中，DE⊥AB于E，DF⊥BC于F，若ABCD的周长为48，DE＝5，DF＝10，则ABCD的面积等于……第2题第3题3．如图，正方形是由k个相同的矩形组成，上下各有2个水平放置的矩形，中间竖放若干个矩形，则k= .。

人教版八年级数学下册《第18章勾股定理》总复习教案教学目标通过课堂教学，学生应该能够：1.熟练掌握勾股定理的定义和证明方法；2.了解勾股定理的应用，能够运用勾股定理解决实际问题；3.了解勾股定理的相关知识，如勾股数、勾股三元组等；4.培养学生的数学思维能力和创造能力。

教学过程1. 引入首先介绍勾股定理的历史背景。

让学生了解勾股定理的起源和发展历程，以及勾股定理在数学及实际中的应用。

2. 定理的讲解和证明2.1 定理的定义在介绍定理前，首先要引入相似三角形和勾股定理的基本知识。

然后讲解勾股定理的定义：在直角三角形中，斜边的平方等于两直角边的平方和。

2.2 定理的证明利用相似三角形的知识，讲解勾股定理的证明方法。

分别从几何和代数两个角度进行证明，让学生了解不同证明方法的优缺点，培养学生的数学思维和创造能力。

3. 定理的应用3.1 计算斜边长和直角边长通过练习题，让学生掌握如何利用勾股定理计算斜边长和直角边长。

3.2 解决实际问题通过实例，让学生了解勾股定理的应用。

如：利用勾股定理测量三角形的周长、面积等。

4. 相关知识4.1 勾股数和勾股三元组讲解勾股数和勾股三元组的概念。

通过练习题，让学生掌握勾股数和勾股三元组的计算方法。

4.2 勾股定理的推广介绍勾股定理的推广知识，如勾股定理的逆定理和勾股定理的推广到不同类型的三角形中。

5. 总结复习通过各种练习题和例题，对勾股定理的相关知识进行总结复习。

帮助学生快速理解和记忆勾股定理及相关知识。

教学方法本教案采用讲授和练习相结合的方式，让学生在理解定理的基础上，通过练习题、实例等方式进行深入学习。

教学重点和难点1. 教学重点勾股定理的定义和证明方法，及其应用。

2. 教学难点勾股定理的证明方法，以及实际问题的应用。

教学工具几何工具、黑板、粉笔、教材、练习册等。

总结通过本次教学，学生应该对勾股定理有更深刻的认识和理解，并能够运用所学知识解决实际问题。

同时，本次教学应该培养学生的数学思维和创造能力，使学生能够更好地适应未来的学习和实际生活。

人教版八年级数学下册《第18章勾股定理》总复习教案三一、回忆交流，协作学习【活动方略】活动设计：教员先将先生分红四人小组，交流各自的小结，并结合课本P87•的小结停止反思，教员巡视，并且不时引导先生进入温习轨道．然后停止小组汇报，汇报时可借助投影仪，要求先生下台汇报，最后教员归结．【效果探求1】〔投影显示〕飞机在空中水平飞行，某一时辰刚好飞到小明头顶正上方4000米处，过了20秒，飞机距离小明头顶5000米，问：飞机飞行了多少千米？思绪点拨：依据题意，可以先画出契合题意的图形，如右图，图中△ABC•中的∠C=90°，AC=4000米，AB=5000米，•要求出飞机这时飞行多少千米，•就要知道飞机在20秒时间里飞行的路程，也就是图中的BC长，在这个效果中，•斜边和不时角边是的，这样，我们可以依据勾股定理来计算出BC的长．〔3000千米〕【活动方略】教员活动：操作投影仪，引导先生处置效果，请两位先生下台演示，然后讲评．先生活动：独立完成〝效果探求1〞，然后积极举手，下台演示或与同伴交流．【效果探求2】〔投影显示〕一个零件的外形如右图，按规则这个零件中∠A与∠BDC都应为直角，•工人徒弟量得零件各边尺寸：AD=4，AB=3，DB=5，DC=12，BC=13，请你判别这个零件契合要求吗？•为什么？思绪点拨：要检验这个零件能否契合要求，只需判别△ADB 和△DBA能否为直角三角形，这样可以经过勾股定理的逆定理予以处置：AB2+AD2=32+42=9+16=25=BD2，得∠A= 90°，同理可得∠CDB=90°，因此，这个零件契合要求．【活动方略】教员活动：操作投影仪，关注先生的思想，请两位先生上讲台演示之后再评讲．先生活动：思索后，完成〝效果探求2〞，小结方法．解：在△ABC中，AB2+AD2=32+42=9+16=25=BD2，∴△ABD为直角三角形，∠A=90°．在△BDC中，BD2+DC2=52+122=25+144=169=132=BC2．∴△BDC是直角三角形，∠CDB=90°因此这个零件契合要求．【效果探求3】甲、乙两位探险者在沙漠停止探险，某日早晨8：00甲先动身，他以6•千米／时的速度向东行走，1小时后乙动身，他以5千米／时的速度向北行进，上午10：00，•甲、乙两人相距多远？思绪点拨：要求甲、乙两人的距离，就要确定甲、乙两人在平面的位置关系，由于甲往东、乙往北，所以甲所走的路途与乙所走的路途相互垂直，然后求出甲、乙走的路程，应用勾股定理，即可求出甲、乙两人的距离．〔13千米〕【活动方略】教员活动：操作投影仪，巡视、关注先生训练，并请两位先生上讲台〝板演〞．先生活动：课堂练习，与同伴交流或举手争取下台演示。

第18章平行四边形复习一、复习目标1、经历平行四边形基本性质，常见判定方法的复习交流过程，使学生学会“合乎逻辑地思考”，建立知识体系，获得一定的技能基础．2、让学生理解平面几何观念的基本途径是多种多样的，感知和体验几何图形的现实意义，体验二维空间相互转换关系．3、通过对正方形的探索学习，体会它的内在美和应用美.二、课时安排1课时三、复习重难点重点：平行四边形的性质以及判定．难点：定理的综合应用．四、教学过程(一)知识梳理1、平行四边形定义：2、平行四边形的性质：3、平行四边形的判定：4、三角形的中位线概念：5、三角形的中位线三角形的第三边，且等于第三边的 .6、一个三角形有中位线。

(二)题型、技巧归纳考点一平行四边形的定义例1、如图， ABCD中，∠A=120°，则∠1= 。

考点二平行四边形的性质例2．平行四边形ABCD中，AB=6cm，AC+BD=14cm ，则△AOB的周长为多少？考点三平行四边形的判定例3、点A、B、C、D在同一平面内，从①AB//CD；②AB＝CD；③BC//AD；④BC＝AD四个条件中任意选两个，不能使四边形ABCD是平行四边形的选法有（）A．①②B．②③C．①③D．③④考点四三角形中位线例4．△ABC中，D、E分别为AB、AC的中点，若DE＝4，AD＝3，AE＝2，则△ABC的周长为。

（三）典例精讲1.如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD的长为( )A.4cmB.5cmC.6cmD.8cm2.如图,在周长为20cm的▱ABCD中,AB≠AD,AC,BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为( )A.4 cmB.6 cmC.8 cmD.10 cm3.如图,在平行四边形ABCD中,AD=5cm,AB⊥BD,点O是两条对角线的交点,OD=2 cm,则AB=＿＿＿＿＿＿cm.4.如图所示,平行四边形ABCD中,对角线AC,BD相交于点O,过点O的直线分别交AD,BC于点M,N,若△CON的面积为2,△DOM的面积为4,则△AOB的面积为＿＿＿＿＿＿.5.如图,在▱ABCD中,对角线AC,BD相交于点O,如果AC=14,BD=8,AB=x,那么x的取值范围是＿＿＿＿＿＿.6.已知,如图,O为▱ABCD的对角线AC的中点,过点O作一条直线分别与AB,CD交于点M,N,点E,F 在直线MN上,且OE=OF.(1)图中共有几对全等三角形?请把它们都写出来；(2)求证:∠MAE=∠NCF.（四）归纳小结1．本节课学习了哪些主要内容？2．在平行四边形的综合应用时要注意哪些问题？（五）随堂检测1．在平行四边形ABCD中，∠A=70°，∠D= , ∠BCD=______．2.平行四边形的两邻边分别为6和8，那么其对角线应（）A．大于2， B．小于14C．大于2且小于14 D．大于2或小于123、如图，平行四边形ABCD中，AB=5，AD=8，∠ BAD 、∠ADC的平分线分别交BC于点E、F上，则EF= 。

第十八章平行四边形【教学目标】1、通过对几种平行四边形的回顾与思考，使学生梳理所学的知识，系统地复习平行四边形与各种特殊平行四边形的定义、性质、判定方法；2、正确理解平行四边形与各种特殊平行四边形的联系与区别，在反思和交流过程中，逐渐建立知识体系；3、引导学生独立思考，通过归纳、概括、实践等系统数学活动，感受获得成功的体验，形成科学的学习习惯。

【教学重点】1、平行四边形与各种特殊平行四边形的区别。

2、梳理平行四边形、矩形、菱形、正方形的知识体系及应用方法。

【教学难点】平行四边形与各种特殊平行四边形的定义、性质、判定的综合运用。

【教学模式】以题代纲，梳理知识-----变式训练，查漏补缺 -----综合训练，总结规律-----测试练习，提高效率【教具准备】三角板、实物投影仪、电脑、自制课件。

【教学过程】一、以题代纲，梳理知识（一）开门见山，直奔主题同学们，今天我们一起来复习《平行四边形》的相关知识，先请同学们迅速地完成下面几道练习题，请看大屏幕。

（二）诊断练习1、根据条件判定它是什么图形，并在括号内填出，在四边形ABCD中，对角线AC和BD相交于点O：(1) AB＝CD,AD＝BC （平行四边形）(2)∠A＝∠B＝∠C＝90°（矩形）(3)AB＝BC，四边形ABCD是平行四边形（菱形）(4)OA＝OC＝OB＝OD ，AC⊥BD （正方形）(5) AB＝CD, ∠A＝∠C ( ？ )2、菱形的两条对角线长分别是6厘米和8厘米，则菱形的边长为5厘米。

3、顺次连结矩形ABCD各边中点所成的四边形是菱形。

4、若正方形ABCD的对角线长10厘米，那么它的面积是50平方厘米。

5、平行四边形、矩形、菱形、正方形中，轴对称图形有：矩形、菱形、正方形，中心对称图形的有：平行四边形、矩形、菱形、正方形，既是轴对称图形，又是中心对称图形的是：矩形、菱形、正方形。

（二）归纳整理，形成体系1、性质判定，列表归纳2、基础练习：（1）矩形、菱形、正方形都具有的性质是（C）A．对角线相等（距、正） B. 对角线平分一组对角（菱、正） C．对角线互相平分 D. 对角线互相垂直（菱、正）（2）、正方形具有，矩形也具有的性质是（A）A ．对角线相等且互相平分 B. 对角线相等且互相垂直C. 对角线互相垂直且互相平分D. 对角线互相垂直平分且相等 （3）、如果一个四边形是中心对称图形，那么这个四边形一定（ D ） A ．正方形 B ．菱形 C ．矩形 D ．平行四边形 都是中心对称图形，A 、B 、C 都是平行四边形 （4）、矩形具有，而菱形不一定具有的性质是（ B ）A. 对角线互相平分B. 对角线相等C. 对边平行且相等D. 内角和为360问：菱形的对角线一定不相等吗？错，因为正方形也是菱形。