Mathematica在简谐振动合成分析中的应用

用Mathcad 解决物理问题一：受迫振动实验原理：用一个周期性的外力作用于一个阻尼振动系统，以补充阻尼振动过程中能量的损失。

这种周期性的外力称为策动力，在策动力作用的振动称为受迫振动。

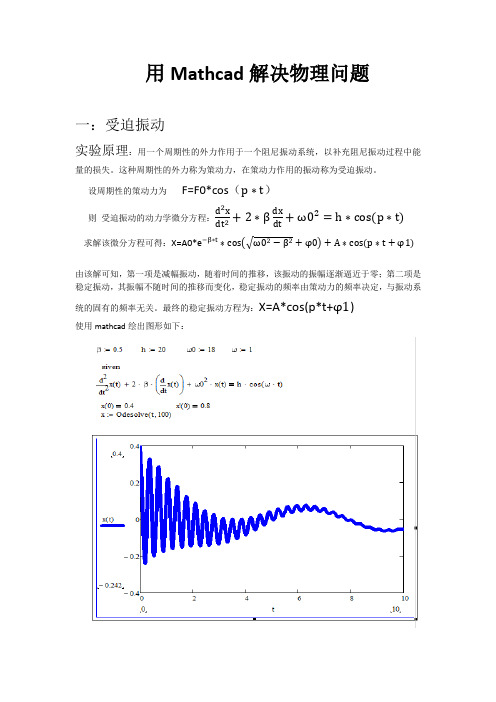
设周期性的策动力为 F=F0*cos （p ∗t ）则 受迫振动的动力学微分方程：d 2x dt 2+2∗βdx dt +ω02=h ∗cos ⁡(p ∗t)求解该微分方程可得：X=A0*e −β∗t ∗cos ω02−β2+φ0 +A ∗cos ⁡(p ∗t +φ1)由该解可知，第一项是减幅振动，随着时间的推移，该振动的振幅逐渐逼近于零；第二项是稳定振动，其振幅不随时间的推移而变化，稳定振动的频率由策动力的频率决定，与振动系统的固有的频率无关。

最终的稳定振动方程为：X=A*cos(p*t+φ1) 使用mathcad 绘出图形如下：二：同方向，不同频率的简谐振动的合成实验原理：设两个分振动的频率分别为ω1和ω2，振幅均为A0，由于频率相同，总有某时刻两个分振动的旋转矢量重合，即二者相位相同，为简化问题同时不失一般性，我们把此刻记为时间零点，这样，两个分振动可以分别设为X1=A0*cos(ω1∗t+φ)X2=A0*cos(ω2∗t+φ)故合振动的振动方程为X=X1+X2=A0*cos(ω1∗t+φ)+A0*cos(ω2∗t+φ)=2*A0*cos(ω2−ω1∗t/2)*cos((ω2+ω1)*t/2+φ) 该式表明，不同频率的简谐振动，其合振动不再是一个简谐振动。

如果两个振动的频率都较大而其差较小，振幅部分比起相位部分变化缓慢得多，这样产生振动的振幅时而加强，时而减弱的现象称为拍。

使用mathcad绘出图形如下：三：光栅衍射的光强分布实验原理：一束平行光照射到光栅上，透过光栅在透镜的焦平面处的屏上就得到一组光栅衍射图形。

显然，通过光栅不同的缝的光要发生干涉，而每条缝发出的光本身会产生衍射。

因此，光栅衍射图形是单缝衍射和缝间多光束干涉的综合效果。

教学工作者通过Mathematica的互动型教学模式激发学生的兴趣，加深他们的理解，使学生拥有丰富的技能面向自己的未来。

科研工作者可以应用Mathematica快速准确地分析科研数据、验证理论假设、整理研究结果。

因为Mathematica提供越来越多的功能，可替代多种专门软件，院校单位能够以低廉的价格在全校园范围内使用教学应用集强大的计算能力、动态可视化引擎、专业水准的文件处理与演示工具为一体，Mathematica为组织教学材料提供了一个完整划一的工作环境。

您再也不必在不同的软件间跳来跳去就可完成您要做的一切。

从理念到教学计划不管您是在做课程设计还是对其进行修改，Mathematica将帮您组织、测试你的构想，使之迅速形成一个现实的教学计划。

主要性能:在课堂上求解问题用二维或三维图形演示数据或函数用随时可用的数据集来分析真正的数据在同一文档中对讲义、方程、例题计算、图形、参考资料及超链接进行编译函数参考:数学函数»公式推演»方程求解»矩阵与线性代数»微积分»最优化»统计»多项式代数»离散数学»数论»逻辑与布尔代数»数据可视化»函数可视化»符号化图语言»计算几何学»可计算数据»设计与演示演讲内容Mathematica让您把所有您制作的演讲材料，包括讲义、方程、示例、图形、演示等等，融入一个动态演示中。

而且你还可以随意对其进行修改。

主要性能:以标题、章节、列表等方式为您的文档设计格式即时撰写讲义或提纲将文档转换成互动型幻灯片，具有完全可编辑的互动型内容通过一个电子白板，用工具栏与您的文档互动，可以不用键盘函数参考:用Mathematica演示»笔记本基础»笔记本格式与风格设计»文档生成»生成专业化格式文档(新功能)无论是制定教学大纲、授课安排，抑或是给学生布置作业、设计试卷，Mathematica让您自如地在您的文档中引入技术元素而根本不影响其美观。

Mathematica数值计算在量子力学谐振子的应用Mathematica 在量子谐振子的应用杨宇轩南漳县第二中学摘要：本文使用数值计算的方法,解量子力学中的谐振子的薛定谔方程，得到波函数和能量本正值间的关系。

关键词: 量子谐振子；数值计算；能量本征值；波函数；Mathematica引言在自然界中存在大量的振动现象。

经典物理中，复杂的振动系统往往可以分解为若干个简单的简谐振动，而这些做简谐振动的系统就是具有深刻意义的谐振子系统。

因此对于经典物理，对于谐振子的研究形成了振动理论的大部分内容。

同样地，在量子力学的力学系统中一个简单而有意义的例子是谐振子。

谐振子对于普遍理论有重要的意义，因为它是形成辐射理论的基础。

在普遍理论中，对于谐振子动力学方程的求解最终归结为求解二阶线性微分方程。

经典理论中对于谐振子的求解是非常容易的，然而，在量子力学中，谐振子的求解就是求解谐振子的薛定谔方程；对于薛定谔方程的求解却并不容易，需要借用特殊函数才能求解。

本文将采用数值计算的方法，通过波函数的自然条件，分析得出一维谐振子的能量本正值应当满足的条件。

[1-3] 谐振子的薛定谔方程考虑一个作一维小振动的粒子（线性振子），该粒子的势能为：221m 2x ω （1）该振子的哈密顿量[4]为： 22222pm x H mω=+ （2）可以得到谐振子定态薛定谔方程[4]为：2222[]22m x E m ωψψ-?+= （3）通过求解数学物理方程以及一些特殊函数，可得到谐振子的波动方程[4]为： 21421()()2!m x n n n m m e H x n ωωωψπ-= （4）列出，n H 的前五项[5]： 0122323424535()1()2()42()812()164812()32160120H H H H H H ξξξξξξξξξξξξξξξ===-=-=-+=-+ （5）由，公式（4）、（5），我们可以看出，对于波函数及其一阶导数满足：(0)0n ψ= 当21n k =+ （7） (0)0nψ'= 当2n k = （8）其中，0,1,2,3...k =谐振子的能量的数值分析通过化简，谐振子的能量本征值方程[5]，可以写为：222()d K d ψξψξ=-（9）其中，m x ωξ= ；2E K ω= 。

一、问题的引入 回顾旋转矢量：从坐标原点O(平衡位置)画一矢量A ，使它的模等于谐振动的振幅A ，并令t=0时A 与x 轴的夹角等于谐振动的初位相ϕ，然后使A 以等于角频率ω的角速度在平面上绕O 点作逆时针转动，这样的矢量称为旋转矢量。

二、同方向简谐振动的合成a) 最简单的情况：频率相同设一个质点同时参与两个独立的同方向、同频率的简谐振动 i. 两个旋转矢量的合成111cos()x A t ωφ=+，222cos()x A t ωφ=+()()()121122+=cos()+cos()=cos()x t x t x t A t A t A t ωϕωϕωϕ=+++其中A ，ϕ分别为合振动的和振幅和初相位。

由矢量合成平行四边形法则，则两旋转矢量的合矢量A 为12+A A A =ii. 合成后的新旋转矢量 合成后的新旋转矢量由矢量合成图可知，新旋转矢量合振幅A 为：00新课引入，回顾上节课内容03强调：同方向同频率简谐振动合成强调平行四边形矢量合成法则22121221=2cos()A A A A A ϕϕ++-合振动的初相为：11221122sin sin tan cos cos A A A A φφϕφφ+=+iii. 合成振动加强和减弱的相位差条件当相位差()21=20,1,....k k ϕϕπ-=±，则振动相互加强两简谐振动的相位相同，合振动振幅为A = A 1 + A 2 （相互加强）当相位差()()21=210,1,....k k ϕϕπ-+=±，则振动相互减弱两简谐振动的相位相反，合振动振幅为A = A 1 - A 2 （相互削弱）一般情况下： A 1 + A 2 > A > A 1 - A 2结论：同方向，同频率的两个简谐振动的合振动仍然是简谐振动，并保持原来的振动方向和频率不变。

b) 振动合成一般情况：两个同方向，不同频率简谐振动合成 i. 特殊情形：合成前两简谐振动频率之差很小由于相位差随着时间改变，合振动一般不再是简谐振动。

Mathematica在振动波问题中的应用鲍四元;孙洪泉;陈旭元【摘要】基于运用Mathematica软件的强大的符号运算功能和作图功能,分析其在振动波问题教学中的现实意义,给出了学习振动波与使用Mathematica的有机结合的方法.【期刊名称】《物理与工程》【年(卷),期】2010(020)004【总页数】4页(P49-51,64)【关键词】Mathematica;振动波问题;有机结合;学习兴趣【作者】鲍四元;孙洪泉;陈旭元【作者单位】苏州科技学院土木工程学院,江苏,苏州,215011;苏州科技学院土木工程学院,江苏,苏州,215011;苏州科技学院土木工程学院,江苏,苏州,215011【正文语种】中文数学软件的开发和应用,大致上是从20世纪70年代开始的,常用的有 M aple、Matlab、M athCAD、Mathematica等,以 Mathematica为例,这里对该类软件进行扼要的介绍.M athematica是由美国物理学家Stephen Wo1fram开发的,是一种集数学计算、处理与分析于一身的软件,拥有从多项式运算到微积分、特殊函数分析运算等丰富的功能,能支持相当复杂的符号运算、数值运算,并提供可视化输出.它可以解决许多数学问题而不用编制大量的程序,操作简单、易学、易用.它还是一个交互式计算系统,计算是在用户和Mathematica系统之间互相交换、传递信息数据的过程中完成的.Mathematica系统所接受的命令都被称作“表达式”,系统在接受了一个表达式后就对它进行处理,然后返回计算结果.在输入一个数学公式、方程组、矩阵等之后计算机能直接给出结果,用户无需考虑中间的计算过程.具有强大的符号计算功能是该软件的一个显著特点,它直接支持符号运算,用户只要在计算机上输入数学公式、符号和等式等,就可以很容易地算出代数、积分、三角以及很多科技领域中的复杂表达式的值.同时它又具有显示数学表格和图形功能,可以数据作图、参数作图、函数作图和动画演示,从而使用户对问题的理解、分析更加形象和具体. Mathematica系统带有丰富的子程序软件包,方便各种专业人员使用. Mathematica在学生学习振动波问题及应用相关知识方面有着重要的现实意义. 振动波问题中,涉及很多关于函数的极限、导数、微分、积分的运算,并且涉及到许多复杂的技巧变换和运算,学生往往要花费大量的时间来计算和练习,以致有的学生产生了畏惧和逃避心理.其实,在学习振动波问题时,如果学生通过老师的讲解,能够对概念的本质、来龙去脉和其中的思想方法达到一定程度的理解和领会后,而涉及表达式的运算完全可以借助M athematica软件的命令来完成.从而节省了很多时间可用于理解力学概念、思想方法,并进行分析问题和解决问题的练习,同时也使运算能力不再成为学好和掌握振动波问题知识的绊脚石.下面简介Mathematica在振动波问题中的若干符号计算功能和应用.求显函数的低阶导数、一元显函数的高阶导数和二元显函数的偏导数分别有格式命令如下:D[表达式,{求导变量,m}]用于求m阶导数;D[f,x],求f对x的偏导数D[f,{x1,x2,...}],求f对 x1,x2,...的高阶偏导数D[f,{x,m}],求f对x的m阶偏导数.如下例求积分一直是学生反映比较花费时间的问题,M athematica的积分命令会使学生感觉积分易如反掌.1)求不定积分的格式为Integrate[被积表达式,积分变量].2)求定积分的格式为 Integrate[被积表达式,{积分变量,下限,上限}].3)求二重积分的格式为Integrate[Integrate[f(x,y),{y,h(x),g(x)}],{x,a,b}]可类推到多重积分.也可用格式:Integrate[积分表达式,{积分变量1,下限,上限},{积分变量2,下限,上限}].如计算,其中D是由0≤x≤1和 y=x2围成.可输入 Integrate[Integrate[x＊y 2,{y,x 2,2x)],{x,0,1)]直接运行即得结果M athematica的Eigenvalues和Eigenvecto rs两个命令可用来求系统固有频率和主振型.如图1所示系统,已知 m1=m2=m3=m,k1=2k,k2=k3=k,试求出系统的固有频率和正则振型矩阵.多自由度系统的广义特征值问题中,Kφ =ω2Mφ,其中特征矩阵为 M-1K,ω2是特征矩阵的特征值,φ是特征矩阵的特征向量,M为质量矩阵,K为刚度矩阵.图1系统中M矩阵和 K矩阵如下对于一般初等函数作图,无论函数多简单或复杂,只要输入Mathematica命令,就可以很快画出图像.画图命令的格式为:Plot[函数表达式,{自变量,下限,上限)]如在介绍惯性式测振仪的基本原理时,幅频特性曲线如下相对阻尼系数ξ取0,0.3,0.4,0.5,0.6,0.7,1,2,5和10时的图形,可通过输入如下命令得到.运行后可得到图2.在Mathematica中,可以编制动画程序,演示出图形形成的过程,这样便于学生对图形形成过程的想象和理解.下面演示球面的形成过程.执行:循环程序语句,可形成一系列不同旋转角度的图形(见图3),双击任一图形就可以看到球面形成过程的动画演示(此对v变化播放,同样可调成对u播放),学生对参数的意义会有更深的理解.另外,选中所绘的一系列图形,点击 Cell菜单,然后执行Animate Selected Grapics,可以动画形式播放图形.设计出一维波动的Mathematica仿真程序.其中输入参数:振幅A,频率ω,波速v;中间变量:显示范围xmax,时间的范围tmax,抽样时间间隔dt.其输出为仿真图像.源程序:一维振动传播的仿真图像[4]运行后得到一串图片,然后可再对这些图片显示动画效果.图4展示了在振动传播的过程中四个瞬时各质点的运动情况.Mathematica强大的图形处理功能,能快速作出平面图形和立体图形.同时,M athematica所绘图形既美观漂亮又易于实现动画效果,可大大激发学生学习兴趣. Mathematica的强大功能对学生学习振动波问题的意义,使我们认识到,让先进的软件辅助振动波问题的学习是现代化教学的需要.但这一认识的付诸实施,还需师生的共同努力.一方面,需要师生共同解放思想、转变观念,积极倡导和使用.Mathematica是信息时代给我们提供的宝贵资源,教学中应用它来改变学生的学习方式和现状,学习效果一定会有显著的改观.另一方面,对 Mathematica的局限性应有充分的认识,不能盲目的依赖.Mathematica对振动波问题的学习只是一种辅助作用,即使有强大的数学软件仍然要注意严密的逻辑思维的训练.学习振动波问题时,理论、技术、方法的学习仍然是重中之重.总之两方面不可偏颇,只有将学习过程和使用M athematica有机结合起来才能真正产生满意的效果.【相关文献】[1] Stephan Wolfman.Mathematica全书(特别版)[M].周孝方译.西安:西安交通大学出版社,2002[2] 丁大正.科学计算强档M athematica 4教程[M].北京:电子工业出版社,2002[3] 洪维恩编著,魏宝琛改编.数学运算大师Mathematica4[M].北京:人民邮电出版社,2002[4] 张新,倪致祥.基于Mathematica的振动传播演示[J].阜阳师范学院学报(自然科学版),2008,25(2):31～33。

Mathematica模拟简谐振动的合成陈大伟;斯小琴【期刊名称】《物理通报》【年(卷),期】2017(0)4【摘要】按照一维、二维相互垂直和三维相互垂直3种情形,运用Mathematica 软件分别模拟了同频率和不同频率的简谐振动合成.直观地显示了不同情况下简谐振动合成的结果,不但可以加深学生对各种简谐振动合成的理解,还可以提高学生的学习兴趣.%In this paper,three cases are given of one dimensional,two dimensional and three dimensional,using mathematica to simulate the same frequency and different frequency synthesis of harmonic vibration.To display the different conditions of the synthesis of harmonic vibration results,not only can deepen students′ understanding of the synthesis of various harmonic vibration,but also can improve the students' interest in learning.【总页数】4页(P111-114)【作者】陈大伟;斯小琴【作者单位】安徽建筑大学城市建设学院安徽合肥 238076;安徽建筑大学城市建设学院安徽合肥 238076【正文语种】中文【相关文献】1.简谐振动合成的计算机模拟 [J], 向根祥;石玉军;2.Mathematica在简谐振动合成分析中的应用 [J], 全桂英3.简谐振动合成的计算机模拟 [J], 向根祥;石玉军4.基于MATLAB的简谐振动合成模拟分析 [J], 苏玉霞5.基于MATLAB的简谐振动合成模拟分析 [J], 苏玉霞;因版权原因，仅展示原文概要，查看原文内容请购买。

由三角波生成的李萨如图形李京颍;黄静【摘要】By the numerical simulation function of scientific computing software Mathematica, a series of Lissajous' figures generated by the triangular wave are studied, and compared with the standard Lissajous' figures." The results show that division vi- bration being as simple harmonic motion is not a necessary condition for the topological properties of the Lissajous' figures.%利用科学计算软件Mathematica的数值模拟功能，研究了一类由三角。

波生成的李萨如图形，并与标准的李萨如图形进行了比较。

结果表明对于李萨如图形的拓扑性质来说，分振动为简谐振动并不是必要条件。

【期刊名称】《阜阳师范学院学报（自然科学版）》【年(卷),期】2012(029)004【总页数】4页(P17-20)【关键词】Mathematica;三角波;李萨如图形【作者】李京颍;黄静【作者单位】阜阳师范学院物理与电子科学学院,安徽阜阳236037;阜阳师范学院物理与电子科学学院,安徽阜阳236037【正文语种】中文【中图分类】O321在一般情况下，两个互相垂直但频率不同的简谐振动合成时，由于相位差不是定值，合运动的轨迹将是不稳定的。

若两个分振动的频率比为有理数，即频率之比为简单的整数比时，则合成运动又具有稳定的封闭的运动轨迹。

描述这些运动轨迹的图形称为李萨如图形，在工程技术领域，常利用李萨如图形进行频率和相位的测定[1-5]。

李萨如图形的动态模拟及其在声速测量中的应用姚雪; 陈学文; 张家伟; 都进学【期刊名称】《《重庆科技学院学报（自然科学版）》》【年(卷),期】2019(021)005【总页数】4页(P50-53)【关键词】声速测量方法; 李萨如图形; Mathematica软件; 实验教学【作者】姚雪; 陈学文; 张家伟; 都进学【作者单位】重庆科技学院数理与大数据学院重庆 401331【正文语种】中文【中图分类】O422.1当质点同时参与两个相互垂直方向的简谐振动，质点的位移是这两个振动的位移的矢量和。

如果两个振动的频率具有简单的整数比值的关系，质点的轨道是稳定的运动轨道，这些轨道曲线即李萨如图形(Lissajous-Figure)。

利用李萨如图形可以测量两正弦电压相位差、交流电的频率、交流阻抗特性、音叉频率以及两个相互垂直的简谐振动的相位差及频率等。

两个简谐振动的合成问题，尤其是两个相互垂直的不同频率的简谐振动之间的合成问题，是机械振动研究的重要内容，也是大学物理教学的重点和难点部分。

在声速测量实验教学中，为帮助学生理解相互垂直的不同频率的简谐振动合成问题，掌握李萨如图形法的原理及其操作技术，我们借助Mathematica软件，模拟不同频率、不同振幅、不同相位差情况下的合振动的运动情况和轨迹形状，让学生观察各种情况下的动态李萨如图形，取得了较好的教学效果。

1 对李萨如图形的动态模拟Mathematica计算软件具有强大的数值计算、符号运算和图像处理功能，其图形界面友好，输入简单的语句就可以绘制出精美的二维和三维图形。

我们运用Mathematica 8.0.4来绘制李萨如动态图形。

设两个相互垂直的简谐振动分别在x轴和y轴上进行，位移分别为：(1)式中：A1、A2为振幅；ω1、ω2为角频率；φ1、φ2为初相位；t为时间。

在Mathematica中，利用Manipulate命令，可得如图1所示的李萨如图形。

图1中，ω1和ω2在1～6 rads的范围内，以0.01 rads的步长改变；A1和A2在0～1 cm的范围内以0.01 cm的步长改变；φ1和φ2在0～2步的范围内以0.01 rad的步长改变。