当前位置：文档之家 › 16-4 简谐振动的合成

16-4 简谐振动的合成

  • 格式：ppt
  • 大小：1.17 MB
  • 文档页数：35

下载文档原格式

  / 35

合集下载

2、简谐振动的合成

2、简谐振动的合成

A A1 A2
x
x1 A1 cos t x2 A2 cos(ωt π ) x x ( A2 A1 ) cos(ωt π)
o 2
A 2
A1
o
T
t
A
1) 相位相同 φ2 φ1 或 Δφ φ2 φ1 0
A A1 A2
相互加强
x A cos( t 1 ) A cos( t 2 ) 2) 相位相反 Δφ φ2 φ1 π
此结论对讨论各种波的干射、衍射极为有用。
二、 两个同方向不同频率简谐振动的合成 x1 A1 cos 1t A1 cos 2 π 1t
x2 A2 cos 2t A2 cos 2 π 2t
讨论 A1 A2 ,
x x1 x2
2 1 1 2 的情况
x y 2 1 2 A1 A2
π y A2 cos( t ) 2 0 质点沿顺时针方向运动
2 2
y
A1
A2
o
x
A2 y

x A1 cos t
o
A1
x
2 质点沿逆时针方向运动
用 旋 转 矢 量 描 绘 振 动 合 成 图
两 相 互 简 垂 振 直 动 同 的 频 合 率、 成 不 图 同 相 位
1 1 可见 π ( 2 1 )T拍 ∴ T拍 2 1 拍
拍 2 1
拍频（振幅变化的频率）
注意:书上的拍频写成，此处的拍频写成拍
2 1 1 2
( 1 2 ) / 2 1 2 , 1 2
(C)
3k / m /( 2π )

简谐振动的合成

简谐振动的合成

简谐振动的合成
琴弦能发出悠长悦耳的声波,实际上是琴弦上若干种频率振动的合成.若有两列波同时在空间传播,则在相遇区域内,各体元的振动是这两列波在该处引起的振动的合成.
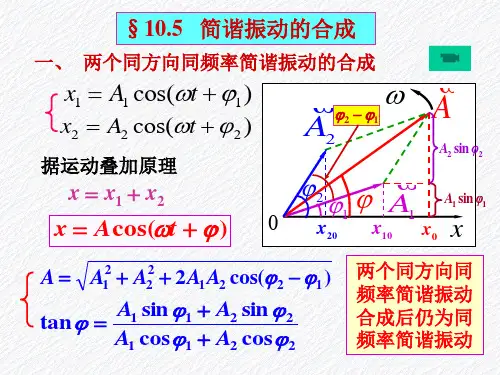
(一)同方向同频率简谐振动的合成
设质点参与同方向同频率的两个简谐振动
X1=A1cos(wt+a1),
X2=A2cos(wt+a2),
式子中x1,x1,A1,A2以及a1，a2分别表示两个振动的位移、振幅和初相位，w0表示它们共同的频率，因两分振动在同方向上进行，故质点合位移等于分位移的代数和：X=x1+x2
=A1cos (w0t+a1)+A2cos (w0t+a2)
将余弦函数展开再重新并项，得
X=（A1 cosa1+A2 cosa2）cosw0t-（A1sina1+A2sina2）sin w0t
式中A1 、A2、a1、a2都是决定的常数，将它们记作Acosa和Asina
于是
X=Acosacosw0t-Asinasinw0t
=Acos（w0t+a）
可见，同方向同频率的两个简谐振动合成后仍为简谐振动，其频率与分振动频相同。

简谐振动的合成

简谐振动的合成

ω2 − ω1 = 2 A cos t cos(ω1t + ϕ ) 2 随t变化缓慢 变化缓慢 随t变化较快 变化较快 合振动不是谐振动。 合振动不是谐振动。
x1
t
x2
t
t
v ω2 A2
x
ω v
ω1 v A 1
理解： 理解：旋转 矢量合成法
A
x
o
x2
x1
x
两 相 互 垂 直 同 频 率 不 同 相 位 差
其合振动的振幅出现时而加强时而减弱的现象-- 拍 其合振动的振幅出现时而加强时而减弱的现象 “拍”。 设 ω1 ≈ ω 2 A1 = A2 = A，
x1 = A cos(ω1t + ϕ )
x 2 = A cos(ω 2t + ϕ )
合成后 x = x1 + x 2 = A cos(ω1t + ϕ ) + A cos(ω 2t + ϕ ) ω2 − ω1 ω2 + ω1 = 2 A cos t cos t +ϕ 2 2
o
ω v A
v A 3 ϕ3
v A 2
v ϕ1 A 1
ϕ ϕ2
x
例：两同方向、同频率谐振动合成， 两同方向、同频率谐振动合成，
x1 = 4 cos 3t
不变， 解：合成后ω不变，
x 2 = 2 cos(3t + π / 3)
求：合成谐振动方程
x = A cos(3t + ϕ )
A=
A + A + 2 A1 A2 cos(ϕ 2 − ϕ1 ) = 2 7 A1 sin ϕ1 + A2 sin ϕ 2 tgϕ = A1 cos ϕ1 + A2 cos ϕ 2

大学物理教程3.2 简谐振动的合成

大学物理教程3.2 简谐振动的合成

Ay tg = A x
A1 sin 1 A2 sin 2 tg A1 cos 1 A2 cos 2
第7章 机械振动
3.2 简谐振动的合成
3. 两种特殊情况
2 A A12 A2 2 A1 A2 cos(2 - 1 )
(1)若两分振动同相
2- 1=0（2k，k=0,1,2,…）
x =A cos( t+ )
第7章 机械振动
3.2 简谐振动的合成
x =A cos( t+ )
由图知：
Ax = A1cos1 + A2cos2 Ay = A1sin1 + A2sin2 由： A2 = Ax2 + Ay2
y Ay
A A2

o
1
A1 A
x
2
x
2 2 A A1 A2 2 A1 A2 cos( 2 - 1 )
x1 4 cos 3t cm x2 2 cos(3t π) cm
求合成振动的振幅、初相位和振动表达式。
解 这两个谐振动的频率相同 3rad s ，振动方向相 同。所以它们的合成振动仍然是在x方向的、具有相同频 率的简谐振动。
-1
第7章 机械振动
3.2 简谐振动的合成
由于这两个振动反相，因此在旋转矢量图上，振幅矢 量 A1 和 A2 的方向始终相反，而合矢量 A 沿 A1 方向。
A 的模，即合成振动振幅为
A (4 - 2) 2
合振动的初相
1 0
x 2cos 3t cm
合振动的表达式为
第7章 机械振动
3.2 简谐振动的合成
二 同方向不同频率的简谐振动的合成 拍

第二节 两个简谐振动的合成

第二节 两个简谐振动的合成

A12 A22 2A1A2 cos(02 01)
A A12 A22 2A1A2 cos
[注：cos( ) cos cos sin sin ]
A值的讨论，有三种情况：
(1) 2k
cos 1
A A1 A2
A值最大
(2) (2k 1) cos 1
A A1 A2 (3) 为其它值
波器显示屏上出现合成结果的图形，见右图。求x ?
解：
x y
m n
Y方向切点数 X方向切点数
x 3 x y 2 1000
x 1500 Hz
本节小结
同方向
1
2
简谐振动 A A12 A22 2A1A2 cos
同方向 1 2 拍 2 1
垂直方向
x m y n
李萨如图
x y
两个简谐振动的步调比较
同相：若两个简谐振动的频率相同、初相位相同，则两个简谐 振动的位移同时达到最大和最小。
x
1
2
t3
t1
t2
t4
t
0 ,同相
反相：若两个简谐振动的频率相同、初相位相差π，则一个振
动到达最大位移处时，另一个振动到达反向最大位移处。
1
x
t1
t2
t3
t4
t
2
,反相
超前与落后：若两个简谐振动的频率相同，初相位之差为
Y2 B2
1
X 0 t1 0 Y B
t2
2
X A Y 0
X 0 t3 Y B
t4
3 2
X A Y 0
t4 t3
t2
t1 Y超前π/2
右旋振动
t1 t2
t3
t4 Y落后π/2

大学物理,机械振动16-4 简谐振动的合成

大学物理,机械振动16-4 简谐振动的合成

o A1 A2 A3 A4 A5 x
A Ai NA0
A
(k 0,1,2,) 2） N 2k 'π
A5

A4 A
i

3
(k ' kN , k ' 1,2,)
N个矢量依次相接构
成一个闭合的多边形。
O A6
2 1
1t 1
A
1 A1
o
x2
x1
x
x
A12 A22 2 A1 A2 cos
1 2 0
2π ( 2 1 )t
20
( 2 1 )t ( 2 1 )
16.4 简谐振动的合成
A A12 A22 2 A1 A2 பைடு நூலகம்os
11
16.4 简谐振动的合成
* 多个同方向同频率简谐运动的合成
第16章 机械振动
x1 A1 cos(t 1 ) x2 A2 cos(t 2 ) xn An cos(t n )

A A 3
x x1 x2 xn
x A cos(t )
x A cos(t )
两个同方向同频率简谐运动合成后仍为简谐 运动，且其方向和频率与原来相同。
2
16.4 简谐振动的合成
第16章 机械振动
x x1 x2
解 析 法
A1 cos t 1 ＋A2 cos t 2 A1 cos 1 A2 cos 2 cos t A1 sin 1 A2 sin 2 sin t
随 t 变化缓慢 随 t 变化较快 由于振幅是周期性变化的，所以合振 动不再是简谐振动。 讨论

大学物理-14 简谐振动的合成

大学物理-14 简谐振动的合成

1 2
2
Δ 1 2
则
2 A0
cos 1
2
2
t
较
cos 1 2 t
2
随时间变化缓慢得多，
将合成式写成谐振动形式 x A(t)cos t
合振动的振幅
A(t )
2 A0
cos 1
2
2
t
合振动可看做是振幅缓慢、周期变化的谐振动
x
[2
A0
cos
1
2
2
t ]cos
1
2
2
t
1
1
2π
2
2
/22））cos(
t
N 2
1
)
(1) 如果各分振动的初相相同，即 0，则有
sin N
A
A lim a
0
2
sin
Na
o
A1
A2
A3 A4
A5
x
0
2 合振幅最大 同相 A Na
(2) N 2kπ
A4
A3
(k' 1,2,, 但k' kN ) A5
A2
A0
O
A6
A1
x
二、振动方向相同、频率略有差别、振幅相等
（同频率或不同频率）
消去参数 t ，得合运动的轨迹方程： 椭圆方程
x2 A12
y2 A22
2
x A1
y A2
cos(
2
1 ) sin2 (2
1)
一般而言，合振动轨迹为椭圆。椭圆的性质
（方位、长短轴、左右旋）在 A1、A2确定之
后，主要取决于相位差 Δ 2 1
x2 A12
y2 A22

简谐振动的合成

简谐振动的合成
8
合成振动表达式：
x(t ) A cos(1t ) A cos( 2 t )
( 2 1 t ） ( 2 1 )t 2 A cos cos[ ] 2 2
当 1与 2 都很大，且相差甚微时，可将 | 2 A cos( 2 1 )t / 2 |视为振幅变化部分， 合成振动是以 ( 2 1 ) / 2 为角频率的谐振动。
17
2 1 0
2 1

4
2 1

2
3 2 1 4

5 4
3 2
7 4
18
2、如果两个互相垂直的振动频率成整数比，
合成运动的轨道是封闭曲线，运动也具有 周期。这种运动轨迹的图形 称为李萨如图形。 用李萨如图形 在无线电技术 中可以测量频 率：
4
上面得到：
A A12 A22 2 A1 A2 cos( 2 1 )
讨论一：
A1 sin 1 A2 sin 2 arctg A1 cos1 A2 cos 2
k 0,1,2,
合振幅最大。
2 1 2k
A A1 A2
当 A1 A2 称为干涉相长。
2
2 2 0 x 0 令k m 0 x 2 T 0 x(t ) A cos( 0 t 0 )
g 0 g mgl sin 0 2 l l I 为m绕O点转动的转动惯量 O mgh sin I mgh 2 C 0 mgh 0 I I 简谐振动的能量 * 任一简谐振动总能量 mg
x2 y2 2 xy 2 2 cos sin 2 A1 A2 A1 A2
上式是个椭圆方程，具体形状由 ( 20 10 )相位差决定。 质点的运动方向与 有关。当 0 时， 质点沿顺时针方向运动；当 2 时， 质点沿逆时针方向运动。 当 A1 A2 时，正椭圆退化为圆。

简谐振动的合成

简谐振动的合成
25 第17章 振 动
则A=|A1-A2|, 两分振动相互减弱， 当 A1=A2 时, A=0 旋转矢量法处理谐振动的合成

x x1 x2
A2
A
A cos( t )
A A A 2 A1 A2 cos(2 1 )
2 1 2 2
2
O

A1
2 1
1
x
A1 sin 1 A2 sin 2 tan A1 cos 1 A2 cos 2
A1 cos(t x )
y
A2
O
A2 cos(t y )
x2 y2 x y 2 2 cos( 2 1 ) sin 2 ( 2 1 ) A1 A2 A12 A2
即 合成的一般结果是椭圆。 1) y x 0 A2 x A1
y
x 0， y 0 y
1 m ，m, n 2 n
合成轨迹为稳定的闭合曲线—李萨如图
y A 1
x x x y y y
达到最大的次数 达到最大的次数
-A2
0
A2
x 3 例如左图： y 2 x
应用：测定未知频率 周期T是多少? 太阳系的稳定性问题
第17章 振 动
- A1
15
小结 （谐振动合成）
（偏振光干涉的理论基础）
b) Δ π
A2
y


o


y

π c) Δ y 2
A1
x
A1 tan A2



x
正椭圆 若 A A2 1
x
0
Δ π
振动方向旋转 2 太阳光非偏振光 偏振片->线偏振光

同方向、不同频率的简谐振动的合成

同方向、不同频率的简谐振动的合成
合振幅 Acos cost Asin sin t
的仍 简然 谐是 振同 动频 。率
Acos(t )
3
式中：
A A12 A22 2A1A2 cos(2 1)
arctg A1 sin1 A2 sin2 A1 cos1 A2 cos2
可见：
2 1 2k
k 0,1,2,
A A1 A2
2Acos (2 1）t cos[ (2 1)t ]
2
2
当1与2 都很大，且相差甚微时，可将
| 2Acos(2 1)t / 2 | 视为振幅变化部分，
合成振动是以 (2 1) / 2 为角频率的谐振动。
其振幅变化的周期是由振幅绝对值变化来决定， 即振动忽强忽弱，所以它是近似的谐振动.
这种合振动忽强忽弱的现象称为拍。 10
arctg A1 sin 1 A2 sin 2
讨论一：
A1 cos1 A2 cos2
2 1 2k k 0,1,2,
A A1 A2 合振幅最大。
当 A1 A2 称为干涉相长。
A A2
A 2A1
A1
6
讨论二：
2 1 (2k 1)
k 0,1,2,
A2
A | A1 A2 |
A
1动、的2相位1 差0在视缓为慢同地频变率化的，合所成以，质不点过运两动个的振轨
道将不断地从下图所示图形依次的循环变化。
当 0 2 1 时是顺时针转；
sin(
20
10 )
x2 A12
y2 A22
2 xy A1 A2
cos
sin2
上式是个椭圆方程，具体形状由
(20 10) 相位差决定。
质点的运动方向与 有关。当 0 时，

简谐振动的合成

简谐振动的合成

(A1 sin1 A2 sin2 )sint
合振幅
令： A1 cos1 A2 cos2 Acos 代入上式：
A1 sin1 A2 sin2 Asin
2
x ( A1 cos1 A2 cos2)cost (A1 sin1 A2 sin2 )sint
Acos cost Asin sint Acos(t ) x Acos(t )
x1(t) a cost
M aN
x2 (t) a cos(t ) x3(t) a cos(t 2 )
C
R N
A
a3
xN (t) a cos[t (N 1) ]O a1 P
在COM中：A 2R sin(N / 2)
上两式相除得：
在OCP中： a 2Rsin( / 2)
7
A a sin(N / 2) sin / 2
若 A1 A2, A 2A1
2.当 2 1 （2k 1） (k 0,1,2, ) 时,
A
A12
A
2 2
2 A1
A2
cos(
2
1
)
| A1 A2 | 合振动振幅最小。
若 A1 A2, A 0
A2
3.一般情况 | A1 A2 | A | A1 A2 |
5
A A2 A1
A2 A A1 A A1
第二节
简谐振动的合成
1
一、同方向同频率简谐振动的合成
在同一直线上同频率的两个简谐振
动分别为：
x1 A1 cos(t 1),
x2 A2 cos( t 2 )
• 代数方法： 振动合成
x x1 x2 A1 cos(t 1) A2 cos(t 2 )
(A1 cos1 A2 cos2) cost

大学物理简谐运动的合成

大学物理简谐运动的合成
大学物理简谐运动的合 成
目录
• 简谐运动的定义与特性 • 简谐运动的合成原理 • 简谐运动的合成方法 • 简谐运动的合成应用 • 总结与展望
简谐运动的定义与特
01
性
简谐运动的定义
简谐运动
物体在平衡位置附近做往复运动，其位移、速度和加速度随时间按正弦或余弦 规律变化的运动。
简谐运动的数学描述
简谐运动可以用正弦或余弦函数表示，其数学表达式为 $x = Asin(omega t + varphi)$，其中 $A$ 是振幅，$omega$ 是角频率，$varphi$ 是初相。
简谐运动的特性
周期性
简谐运动具有周期性，即物体在每个周期内重复 相同的运动轨迹。
往复性
简谐运动是往复运动，即物体在平衡位置附近来 回振动。
能量守恒
简谐运动过程中，系统的动能和势能相互转化， 总能量保持不变。
简谐运动的分类
自由振动
不受外力作用的简谐运动。
受迫振动
受到周期性外力作用的振动，其振动频率与外力频率 相同或相近。
简谐运动的合成方法
03
旋转矢量法
总结词
旋转矢量法是一种直观且易于理解的方法，用于合成简谐运动。
详细描述
旋转矢量法是通过引入一个旋转矢量来表示简谐运动，该矢量在复平面内以角速 度旋转。通过旋转矢量的长度和角度变化，可以直观地理解简谐运动的合成过程 。
复数法
总结词
复数法是一种基于复数运算的方法，用于合成简谐运动。
自激振动
由系统内部激励产生的振动，不需要外部激励作用。
02
简谐运动的合成原理
线性合成原理
线性合成原理是指两个简谐运动的合成结果仍为简谐运动，其振幅和角频率分别为两个简谐运动振幅 和角频率的线性组合。

高二物理竞赛简谐运动的合成 课件

高二物理竞赛简谐运动的合成 课件

若 1， 2 均较大，而差值较小，则合振动
的“振幅”时而大（为 2A），时而小（为 0）。
这种合振动周期性的时强时弱的现象称作拍
单位时间内振动加强（或减弱）的次数叫拍频。
A(t) 2 A cos 2 1 t
2
合振幅变化的周期
Tb
|
2 1 2
|| 2 2 1
|
b
1 Tb
2 1 2 2
2 1
v拍 | v1 v2 | 或 b=|2-1|
4
x1
1
x2
2
=1 - 2
x
第8章 机械振动
t
t
t
5
第8章 机械振动
6
黑管的振动是由9个不同的简谐运动合成的第8章 机械振动
7
钢琴的振动是由16个不同的简谐运动合成的第8章 机械振动
8
受迫振动
共振危害：
第8章 机械振动
A）160多年前，拿破仑率军入侵到西班牙，在 整齐跨过一铁链桥时坍塌，士兵纷纷落水。
1940年华盛顿的塔科曼大桥建成 同年7月的一场大风引起桥的共振 桥被摧毁
10
第8章 机械振动
11
第8章 机械振动
消除共振
A）消极：阻尼器吸收振动能量 B）积极：共振原理做成机械滤波装置，滤掉 有害波段。或改变系统和外界驱动力频率。
共振的利用
A）电驱蚊器 B）微波炉
C）次声波武器 D）核磁共振
12
B）1906年，俄国士兵在圣彼得堡的卡坦卡河，也 发生同样惨剧，士兵纷纷落水。
C）1940年，美国的Tocoma Narrow Bridge， 在风中发生共振坍塌。唯一伤者为一个记者的长毛 狗，在牺牲前将救它的华盛顿大学专家咬伤。（该 桥曾一度作为休闲好去处）

简谐振动的合成

简谐振动的合成

动振幅周期变化的现象叫拍。
解：③拍现象
A (t) 不论 调 达到正的最大或负的最大，对加强振幅来说，都是等效的，
因此拍的圆频率为：
因此：
拍 20 10
调（拍）
20 10
2 20 10
2 拍
2
拍频为： 调（拍） 2 1
合成图像如下图：
x1 t
x2
t
x
t
程序演示：
MATLAB 程序：
t=[0:0.001:10]; %给出时间轴上 10s,分 10000 个点
%输入两组信号的振幅、频率以及初相
A1=input('振幅 1=');W1=input('频率 1=');a1=input('初相 1=');
A2=input('振幅 2=');W2=input('频率 2=');a2=input('初相 2=');
y1=A1*cos(W1*t+a1);
y2=A2*cos(W2*t+a2); %生成两个正弦波
此时 A A12 A22 2A1A2 cos(2 1) A1 A2 Amin 振动减弱
两个同方向、同频率简谐运动反相合成时，其合振动振幅最小，振幅为两个
分振动振幅之差的绝对值，初相位与振幅大的分振动的初相位相同，合成图像如
下图。
x
x2
o
x
t
x1
分析：同方向不同频率简谐振动的合成 x1 Acos10t , x2 Acos20t
A2 A1
A
x
此时 A A12 A22 2A1A2 cos(2 1) A1 A2 Amax 振动加强

4简谐振动的合成

4简谐振动的合成

ω1 − ω2 << ω1 ≈ ω2
dengyonghe1@
设
A1 = A2 = A，
ω1 ≈ ω 2
x1 = A cos(ω1t + ϕ ) x 2 = A cos(ω 2t + ϕ )
合成后 x = x1 + x 2
= A cos(ω1t + ϕ ) + A cos(ω 2t + ϕ )
x
dengyonghe1@
o
2.注意几点 2.注意几点 (1). 当
Hale Waihona Puke ∆ϕ = ϕ 2 − ϕ1 = 2kπ ( k = 0,±1,±2,L) 时,
两个同相
A=
A + A + 2 A1 A2 cos(ϕ 2 − ϕ1 ) x = A1 + A2
2 1 2 2
合振动振幅最大。 合振动振幅最大。 若
一、同方向同频率的两个简谐振动合成
质点同时参与两个振动， 质点同时参与两个振动，只 研究两个同方向同频率的振动合 成。 分振动
x1 = A1 cos(ωt + ϕ1 ) x 2 = A2 cos(ωt + ϕ 2 )
振动合成
x = x1 + x 2
dengyonghe1@
1.利用矢量法求合振动 利用矢量法求合振动
dengyonghe1@
解：直接代公式： 直接代公式：
A = (90 2 ) + (200 2 ) = 220 2
2 2
200 2 ϕ = tan ( ) = 65.80 90 2
−1
∴ u = 220 2 cos(100πt + 65.8 )

一同频率同一直线上的简谐振动的合成

一同频率同一直线上的简谐振动的合成
§4.4 简谐振动的合成
一.同频率、同一直线上的简谐振动的合成 分振动：x1 =A1cos( t+1 ) x2 =A2cos( t+2 )
合振动： x= x1+x2 = Acos( t+ )
A A1 A2 2 A1 A2cos( 2 1 )
2
2
A1sin1 A2sin 2 tg A1cos1 A2cos 2
x y 2 1 2 A1 A2
y
2
2
合振动不再是谐振动。
y
x
x 左旋
右旋
2 -1=/2
2 -1=-/2
21
两个频率相同、 振幅不同的互
相垂直简谐
Δ=0 Δ=/4 Δ=/2 Δ=3/4
振动的合成
Δ=
Δ=5/4
Δ=3/2
Δ=7/4
22
四.不同频率垂直谐振动的合成 李萨如图形 x =A1cos(1 t+1 ) y =A2cos(2 t+2 )
2， = 0 （临介阻尼）
x e t C1 C 2 t
3， < 0 （欠阻尼）
xe
e
t
t
C cos
1
C e
1
i 0 2 2 t
C2 e
2
i 0 2 2 t

2 2
0 t C2 sin 0 t
2
2 2

( 2 1 )

2
o
x
10
例题4.17 求同方向、同频率、同振幅、依次间相 位差均为的N个谐振动的合振动方程。 光的衍射 解
选择适当的计时起点，使某个简谐振动的初 相为零，则有

高二物理竞赛简谐振动的合成课件

高二物理竞赛简谐振动的合成课件

r1
A1r1A2r2
所以振幅与离波源的距离成反比。如果距波源为单 位距离的点振幅为A则距波源r 处的点振幅为A/r
由于振动的相位随距离的增加而落后的关系， 与平面波类似，球面简谐波的波函数：
yAcos[(tr)]
r
u
3. 波的吸收 波在实际介质中，由于波动能量总有一部分会被介 质吸收，波的机械能不断减少，波强亦逐渐减弱。
体积元内媒质质点动能为 穷能人量的 密孩度子早单当位家体。积介质中所具有的波的能量。
鹰体爱积高 元飞内，媒鸦质栖质一点枝动。能为
志由气于和 振贫动困的是相患位难随兄距弟离，的世增人加常而见落他后们的伴关在系一，起与。平面波类似，球面简谐波的波函数：
桐拍山合万振里动丹忽山强路忽，弱雄的风现清象于老风声
4.2 简谐振动的合成
4.2.1 同方向同频率谐振动的合成
质点同时参与同方向同频率
的谐振动 :
x1(t ) A1 cos(t 1 ) x2 (t ) A2 cos(t 2 )
2
A2
M2 A
1
A1
M1
M
合振动 : x x1 x2
x2
x1 x
x Acos(t )
A A12 A22 2A1 A2 cos(2 1 )
静压力之间的压差。
平面简谐波，声压振幅为
pmuA
声强：声波的能流密度。
I1 pm2 1uA22 2 u 2
频率越高越容易获得较大的声压和声强
引起人听觉的声波有频率范围和声强范围
20~200H 00z
1 W 0 m 2~ 1 1 0 W 2m 2
I0 1012Wm2 测定声强的标准
声强级
IL
log10
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

o A1 A2 A3 A4 A5 x
A Ai NA0
A
(k 0,1,2,) 2） N 2k 'π
A5

A4 A
i

3
(k ' kN , k ' 1,2,)
N个矢量依次相接构
成一个闭合的多边形。
O A6
合振动的轨迹为通过 原点且在第一、第三 象限内的直线。
y
x
合振动仍为谐振动。 质点离开平衡位置的位移：
S x y A A2 cos( t )
2 2 2 1 2
23
16.4 简谐振动的合成
利用旋转矢量合成
第16章 机械振动
y
2
3
0 y
2 1
8 3
1
8 7 6
A2 y x A1
相互加强
2）相位差
2
1， ) 1 (2k 1)π (k 0 ，
A A1 A2
相互削弱
3）一般情况， 当相位差为其它值时，
A1 A2 A A1 A2
7
16.4 简谐振动的合成

第16章 机械振动
5 x1 4 cos(2t ) m , x2 3 cos(2t )m, 6 6 解：1）用解析法，合成后不变， x A cos(2t )
拍在声学和无线电技术中的应用： 用音叉的振动来校准乐器； 利用拍的规律测量超声波的频率； 在无线电技术中，可用来测定无线电波频率以及调制。
19
16.4 简谐振动的合成
方法二：旋转矢量合成法
第16章 机械振动
( 2 1 )t ( 2 1 )
2t 2
A 2 2

A
1 T 2 1
18
16.4 简谐振动的合成
A 2 A1 cos 2 π
第16章 机械振动
2 1
2
t
2 1
2 1 2π Tπ 2
1 T 2 1
拍频（振幅绝对值变化的频率）
所以，拍频是振动 cos(2
2 1
2
t ) 频率的两倍。
（拍在声学和无线电技术中的应用） 振动圆频率

1 2
2
21
16.4 简谐振动的合成
*三 相互垂直的简谐振动的合成
第16章 机械振动
*1、两个同频率相互垂直的简谐振动的合成
x A1 cos(t 1 ) y A2 cos(t 2 )
质点运动轨迹方程：
x y 2 xy 2 2 cos( 2 1 ) sin ( 2 1 ) 2 A1 A2 A1 A2
5
x /cm
1
0.05
1振动在 t = 0时： 1 x10 0 , v10 0 2 2振动在t = 0时：
0
5
0 .1
t /s
2
x20 5cm , v 20 0
2
M2
x1 5 cos(20 t 2) cm x2 5 cos(20 t ) cm
第16章 机械振动
(2 1 )t
振幅 A A 1 cos ) 1 2(
2
A2
t)
( 2 1 )t

2 A1 cos(
拍频
2 1
2
o
2 1
x1 x2 cost A
1t 2t
x2 x1
1 A1
A
x
x
2 1
O
M1
10
x
16.4 简谐振动的合成
第16章 机械振动
x1 5 cos(20 t 2) cm x2 5 cos(20 t ) cm
由旋转矢量法：
M2
2
5 4
A 0 M1 0 M 2
5 2 cm
5 4
2
A
O
M1
x
5 x 5 2 cos(20 t ) cm 4
在一般情况下，这是一个椭圆方程。
22
2
2
16.4 简谐振动的合成
2 2
第16章 机械振动
讨论
x y 2 xy 2 2 cos( 2 1 ) sin ( 2 1 ) 2 A1 A2 A1 A2
1） 2 1 0 或 2π
x y 2 ( ) 0 A1 A2
A2 y x A1
令： 则：
A sin A1 sin 1 A2 sin 2 A cos A1 cos 1 A2 cos 2
x A cos cos t A sin sin t A cos t
3
16.4 简谐振动的合成
旋转矢量法：
第16章 机械振动
A
2 A12 A2 2 A1 A2 cos( 2 1 ) 1 m
例：求合振动方程。已知两同方向、同频率谐振动：
A1 sin1 A2 sin 2 3 tg A1 cos1 A2 cos 2 3
因为当t = 0时
6
合振动方程： x 1 cos(2t / 6) m
A0
A1

A2
x
13
16.4 简谐振动的合成
第16章 机械振动
*二 两个同方向不同频率简谐运动的合成
频率较大而频率之差很小的两个同方向简谐运动的合 成，其合振动的振幅时而加强时而减弱的现象叫拍。 14
16.4 简谐振动的合成
第16章 机械振动
15
16.4 简谐振动的合成
第16章 机械振动
x A cos(t )
两个同方向同频率简谐运动合成后仍为简谐 运动，且其方向和频率与原来相同。
2
16.4 简谐振动的合成
第16章 机械振动
x x1 x2
解 析 法
A1 cos t 1 ＋A2 cos t 2 A1 cos 1 A2 cos 2 cos t A1 sin 1 A2 sin 2 sin t
为了简单起见，讨论两个振幅相同，初相位也 相同，在同方向上以不同频率振动的合成。其振 动表达式分别为：
x1 A1 cos1t A1 cos2π 1t x2 A2 cos2t A2 cos 2π 2t
利用三角函数关系式：
x x1 x2

2
cos cos 2 cos
合成振动表达式：

2
cos
x (2 A1 cos 2π
2 1
2
t ) cos 2πFra bibliotek 2 12
t
16
16.4 简谐振动的合成
第16章 机械振动
x x1 x2 A1 cos2π 1t A2 cos2π 2t 2 1 2 1 x (2 A1 cos 2π t ) cos 2π t 2 2
合振动的轨迹为通过原点且 在第二、第四象限内的直线
合振动仍为谐振动。
x
质点离开平衡位置的位移：
S x y A A2 cos( t )
o
1 A1
2
3 A2
x
多个同方向同频率简谐运动合成仍为简谐运动 假设它们的振幅相等，初相位依次差一个恒量。 12
16.4 简谐振动的合成
第16章 机械振动
xN A0 cos[t ( N 1) ]
讨 论
1） 2kπ
x1 A0 cost x2 A0 cos(t ) x3 A0 cos(t 2 )
x
x
o 2
A 2
A1
A A1 A2 2
o
T
合振动振幅最小。
t
6
A
16.4 简谐振动的合成
第16章 机械振动
A
1）相位差
A A 2 A1 A2 cos( 2 1 )
2 1 2 2
2 1 2k π
A A1 A2
(k 0 ， 1， )
从图中三角形的边角关系，
可得：
A A12 A22 2 A1 A2 cos( 2 1 )
A1 sin1 A2 sin 2 tan A1 cos1 A2 cos 2
合振动的振幅A不仅与 两个分振动的振幅有关， 还取决于两分振动的初相 位差。
4
16.4 简谐振动的合成 讨论

6
A(1cm ) 6
A2 ( 3cm )
5 2 6
合振动方程： x 1 cos(2t / 6) m
9
16.4 简谐振动的合成
第16章 机械振动
例：已知两谐振动的曲线，它们是同频率的谐振动。 求：合振动方程。 解：由图知 A1 A2 5 cm
T1 T2 0.1 s 2 T 20
随 t 变化缓慢 随 t 变化较快 由于振幅是周期性变化的，所以合振 动不再是简谐振动。 讨论
A1 A2 ， 2 1 1 2 的情况
合振动是振幅按 | 2A0cos 2π(ν2-ν1) t /2 | 缓慢变化
的，角频率为 (ν2+ν1 ) /2 的“准周期运动”。
17
16.4 简谐振动的合成
2 1 2 2
第16章 机械振动
A A A 2 A1 A2 cos( 2 1 ) 1）相位差 2 1 2k π (k 0 ， 1， 2,)
x
x
合振动振幅最大。
o A