当前位置：文档之家 › 简谐振动22简谐振动的合成

简谐振动22简谐振动的合成

  • 格式：pptx
  • 大小：2.52 MB
  • 文档页数：22

下载文档原格式

  / 22

合集下载

简谐振动的合成

简谐振动的合成

x

A1
2
o
A A1 A2
o
相互削弱
A
A2
3）一般情况 A1 A2 A A1 A2
21
2.n个同方向同频率简谐运动的合成
x1 A1 cos(t 1) x2 A2 cos(t 2 )

xn

An
cos(t

n
)
x x1 x2 xn
19
讨论 A A12 A22 2A1A2 cos(2 1) 1）相位差 2 1 2kπ (k 0，1， 2,)
x

o
A1
A2
A
A A1 A2
相互加强
20
A A12 A22 2A1A2 cos(2 1) 2）相位差 2 1 (2k 1)π (k 0，1, )
dt 2
J ml 2
d 2
g
2 g
l 2
dt 2 l
cos(t ) m
g
l
T 2π l g
转
A
动
l
正 向
FT m
O
P
10
复摆
M l F
转动正向
O
M mgl sin J J d2
dt 2
l
*C
24
频率较大而频率之差很小的两个同方 向简谐运动的合成，其合振动的振幅时而 加强时而减弱的现象叫拍.
x1 A1 cos1t A1 cos2π1t x2 A2 cos2t A2 cos2π2t
mgl J d2
dt 2
P
令 2 mgl

二、同方向不同频率两个简谐振动的合成剖析

二、同方向不同频率两个简谐振动的合成剖析
同方向不同频率两个简谐振动的合成同方向不同频率两个简谐振动的合成????????2tacos212?????????2?tcos21???21xxxtax11cos?差频?tax22cos??设两振动振幅相同并以它们的初相位都为零时为计时起点位移xto2tt23t2t分振动1分振动2合振动122???为一复杂振动和频振幅周期性变化toxx1x2?着重研究21??相近情况拍现象beat即?1?2?1or?2?x????????2tacos212?????????2tcos21?21xxx??振幅随时间的变化非常缓慢振幅调制因子amplitudemodulationfactor应用cooledit来合成两频率相近的简谐振动问题
A 2R sin N
2
P
R
N
Q

/2
由OPa可看出
A0

2R sin 2
A合
sin N
A A0
2

请大家自行练习！
O
a A0 B
b C
X
sin
2
当N=2k 时的合振幅为零。请记住这个结论！
二.同方向不同频率两个简谐振动的合成
同方向同频率两个简谐振动的合成 ------仍为简谐振动
两个同方向频率相近的简谐振动的合成 为合振幅随时间作缓慢变化的准简谐振动（拍）
合振幅变化的频率即拍频 拍 | 2 1 |
两个振动方向垂直频率相同的简谐振动的合成可能仍 为直线振动（而且是谐振动）也可能是圆运动，和椭 圆运动。
课后实验：
1. 请你测量一根吉他琴弦的振动频率。
2. 敲击盛水的玻璃酒杯能产生清晰的音调.试用 音叉把这些音调校准到你所需要的频率看看是否 能把他们排列起来构成一个八度音阶。

简谐运动的合成

简谐运动的合成
x = ( 2 A1 cos 2 π
ν 2 −ν 1
2
t ) cos 2 π
ν 2 +ν1
2
t
振幅部分 振动频率 ν = (ν 1 + ν 2 ) 2 振幅 A = 2 A1 cos 2 π
合振动频率
ν 2 −ν 1
2
振 动
Amax = 2A1
t
Amin = 0
15
第九章
物理学
第五版
9-5
简谐运动的合成
y
ϕ （1） 2 −ϕ1 = 0或 2 π ） A2 y= x A1
A2
A1
o
x
ϕ （2） 2 − ϕ1 = π ） A2 y=− x A1
第九章 振 动
y
A2
A1
o
x
7
物理学
第五版
9-5
简谐运动的合成
x 2 y 2 2 xy 讨 + 2− cos(ϕ 2 − ϕ1 ) = sin 2 (ϕ 2 − ϕ1 ) 论 A12 A2 A1 A2
A
ϕ1
ϕ
A 1
O
x2
x1
xx
两个同方向同频率简谐运动合成后仍 两个同方向同频率简谐运动合成后仍 合成 频率的简谐 简谐运动 为同频率的简谐运动
第九章 振 动
2
物理学
第五版
9-5
简谐运动的合成
（1）相位差 ∆ϕ = ϕ 2 − ϕ1 = 2k π (k = 0，1，2,⋯ ） ± ± )
x
ϕ
A2
x
o
y = A2 cos(ωt + ϕ 2 )
椭圆方程） 质点运动轨迹 （椭圆方程）
x 2 y 2 2 xy + 2− cos(ϕ 2 − ϕ1 ) = sin 2 (ϕ 2 − ϕ1 ) 2 A1 A2 A1 A2

第三节 简谐运动的合成

第三节 简谐运动的合成

2 1 2k k 0,1,2,
A1
A A1 A2 合振动加强
A2
若两分振动反相:
2 1 (2k 1) k 0,1,2,
A A1 A2
合振动减弱
若 A1=A2 , 则 A=0
A2
A1
课堂练习：
两个同方向同频率的谐振动，振动方程分别为
x1
6102 cos(5t )m，
2
x2
2102 sin(
t
)
A
ω2t
O
ω2
2
ω1
ω1t
A
(ω 2
A1
ω1)
t
2
2
A
A2 1
A2 2
2A1A2cos(2
1)t
x2 x
x1x1
x2
x
当 (ω2 ω1) t时,2kπ
A 有最大值 A A1 A2
当 (ω2 ω1) t (时2k，1) π
A有最小值 A A1 A2
合振动振幅的频率为: (ω2 ω1) 2π
(2) 0, ,2 (或 )时,退化为直线;
(3) , 3 (或 ) 时,为正椭圆,若A1=A2,则退化
为圆.2 2
2
(4)椭圆轨迹内切于边长为2A1和2A2的矩形; (5)0 时,椭圆顺时针方向转;
0(或 2 ) 椭圆逆时针方向转.
四、相互垂直但频率不同的简谐振动的合成
5t)m
则其合振动的振幅为谐振动,振幅为：
（1）0 ；
（2）4cm；
（3）4 5cm ；
2
（4）8 cm。
二、同方向不同频率谐振动的合成
1. 分振动 : x1 A1 cosω1 t x2 A2 cosω2t

第2节_简谐振动的合成

第2节_简谐振动的合成
2
x = ( A1 cosϕ1 + A2 cosϕ2 ) cosωt − ( A1 sinϕ1 + A2 sinϕ2 ) sinωt = A cos ϕ ⋅ cos ωt − A sin ϕ ⋅ sin ωt = A cos(ωt + ϕ ) ∴ x = A cos(ωt + ϕ )
两个同方向、 两个同方向、同频率的简谐振动合成后仍然是一个 简谐振动，且频率不变。 简谐振动，且频率不变。 由
若 A1 = A2 , A = 2A1
= A1 + A2
合振动振幅最大。 合振动振幅最大。
（ ） 2.当 ∆ϕ=ϕ2 −ϕ1 = 2k +1 π ( k = 0,±1,±2,⋯) 时, 当
2 2 A = A1 + A2 + 2A1A2 cos( 2 −ϕ1 ) ϕ
A2
=| A1 − A2 |
A
A2 A1
2 2
ϕ 2 − ϕ1 = π / 2
2 2
x y + =1 A1 A2
•当 当
16
A1 = A2 ,
x +y =A
2
为圆方程
2.
∆ϕ = π / 2
y
8
1 2
y
7 6 5
4
7 6 5
4
8
1 2 2 1
x
3
3
4
播 放 动 画
17
3
5 6 7
x
8
4.
3π (ϕ 2 − ϕ1 ) = 2
9
由于余弦函数绝对值的周期为π。 ω 2 − ω1 t ) 的频率的两倍。 所以， 的频率的两倍。 所以，拍频是振动 cos( 2 即拍频为： 即拍频为：

简谐振动的合成实验

简谐振动的合成实验

简谐振动的合成实验一、实验目的1.掌握谐振动的表达与合振动的分析2.掌握信号的相位、幅度、频率等参数的物理含义3.掌握用示波器观察波形以及测量电压、周期和频率的方法。

4.掌握使用信号发生器。

5.利用李萨茹图分析待测信号的相位频率等信息二、实验仪器Waveace1012型数字示波器1台、DG4062型数字信号发生器一台、传输线2条等。

三、示波器的使用（三四节的内容在实验报告中仅需概述即可）示波器就是显示波形的机器，它还被誉为“电子工程师的眼睛”。

它的核心功能就是为了把被测信号的实际波形显示在屏幕上，以供工程师查找定位问题或评估系统性能等等。

它的发展同样经历了模拟和数字两个时代，如图1和图2所示。

图1 模拟示波器图2 数字示波器模拟示波器采用的是模拟电路（示波管，其基础是电子枪）电子枪向屏幕发射电子,发射的电子经聚焦形成电子束,并打到屏幕上。

屏幕的内表面涂有荧光物质,这样电子束打中的点就会发出光来。

而数字示波器则是数据采集，A/D转换，软件编程等一系列的技术制造出来的高性能示波器。

数字示波器一般支持多级菜单，能提供给用户多种选择，多种分析功能。

还有一些示波器可以提供存储，实现对波形的保存和处理。

模拟示波器显示的波形是连续的，是信号真实的波形，而且反应速度特快。

而数字示波器显示的波形是经过数字电路采样得来的点组成的，是个不连续的波形，采样率越高的示波器，越与真实波形接近，但显示速度没有模拟机快。

反应速度快是模拟示波器最大的优点之一，是数字机很难取代的，比如，在测试某一信号时，模拟示波器能在瞬间显示波形，几乎没有延时，而数字机还需要将测试的信号进过数字电路处理后，再显示出模拟的波形，在显示时间上落后模拟示波器。

在此，我们仅介绍数字示波器的使用情况。

示波器可以将输入的波形在屏幕上显示出来，waveace1012型示波器具有两个输入通道，可以同时测量并显示2路信号的变化波形。

示波器的屏幕可以设置成横坐标为时间t，纵坐标为输入信号的电压量的大小，称为“Y-T”时基，如图所示。

医用物理学教学课件 第二节 两个简谐振动的合成

医用物理学教学课件 第二节 两个简谐振动的合成

A12 A22 2A1A2[cos01 cos02 sin01 sin02]
A12 A22 2A1A2 cos(02 01)
A A12 A22 2A1A2 cos
[注：cos( ) cos cos sin sin ]
t4 t3
t2
t1 Y超前π /2
右旋振动
t1 t2
t3
t4 Y落后π /2
左旋振动
例七
一质点同时参与相互垂直的两个振动：
X

8c

os(
t


)
cm
36
Y 6cos( t ) cm
33
请你画出合振动运动轨迹图。
解：

36

2
2B ∵Y落后π/2，左旋振动
2

2
A0
cos

2
O
X

2 A0
cos 2
1
2
t
注： 2t 1t

1 2
(1

cos
)

cos

2

从角度可分析：
t

2
1
2
t
1t
AA
2 1 t
2
O
X
将A与ωt表达式代入 x Acost
x


2
A0

cos 1
∴画一个2A*2B的矩形，内切
画椭圆，标出左旋箭头即可
2A
（2） 2 m 的情况： 1 n
若频率不相等，但是整数比，则合振动的轨迹 是有规则的稳定的闭合曲线-------李萨如图形。

第二节 两个简谐振动的合成

第二节 两个简谐振动的合成

A12 A22 2A1A2 cos(02 01)
A A12 A22 2A1A2 cos
[注：cos( ) cos cos sin sin ]
A值的讨论，有三种情况：
(1) 2k
cos 1
A A1 A2
A值最大
(2) (2k 1) cos 1
A A1 A2 (3) 为其它值
波器显示屏上出现合成结果的图形，见右图。求x ?
解：
x y
m n
Y方向切点数 X方向切点数
x 3 x y 2 1000
x 1500 Hz
本节小结
同方向
1
2
简谐振动 A A12 A22 2A1A2 cos
同方向 1 2 拍 2 1
垂直方向
x m y n
李萨如图
x y
两个简谐振动的步调比较
同相：若两个简谐振动的频率相同、初相位相同，则两个简谐 振动的位移同时达到最大和最小。
x
1
2
t3
t1
t2
t4
t
0 ,同相
反相：若两个简谐振动的频率相同、初相位相差π，则一个振
动到达最大位移处时，另一个振动到达反向最大位移处。
1
x
t1
t2
t3
t4
t
2
,反相
超前与落后：若两个简谐振动的频率相同，初相位之差为
Y2 B2
1
X 0 t1 0 Y B
t2
2
X A Y 0
X 0 t3 Y B
t4
3 2
X A Y 0
t4 t3
t2
t1 Y超前π/2
右旋振动
t1 t2
t3
t4 Y落后π/2

大学物理-12第十二讲简谐振动的合成、阻尼、受迫振动（001）

大学物理-12第十二讲简谐振动的合成、阻尼、受迫振动（001）

解得 ω = ωr = ω02 − 2β 2
则
A=
2mβ
F0
ω02 − β 2
= Amax
A
β2 β3
β1
ω
β1 > βω2 0> β3
23
2.速度共振—使速度振幅达最大值的状态
v = dx = − Aω sin(ωt − δ )
dt
速度振幅 vm = Aω
而 Aω =
F0ω
m (ω02 − ω2 ) + 4β 2ω2
●合振幅A的大小由两个分振动的初相差决定。
当 Δϕ = ϕ2 − ϕ1 = ±2kπ
(k = 0，1，2") 同相
Y ωK
A2
ωK
A ωK
A = A1 + A2 = Amax
θ2
Δθ θ1
A1
合振动加强
x2 θ x1 x x
4
当 Δϕ = ϕ2 −ϕ1 = ±(2k +1)π 反相
(k = 0，1，2")
ϕ =0
t
19
2. β =ω0（临界阻尼） x = e −βt (C1 + C 2t)
●在临界阻尼时，质点到达平衡位置时速度即减为 零，振动不可能发生。
◆原理常用于阻尼天平等，以减少摆动时间.
3. β >ω0（过阻尼）
x = e − βt (C 1e ω1t + C 2 e −ω1t )
●过阻尼时，质点的速度 x
F强 = F0 cosωt
v = dx = Aω cos ωt v与强迫力同位相。
dt
●在整个周期内外力的方向和物体运动方向一致， 不断对物体作正功，使振动最强。 ◆外力的周期性变化与物体的固有振动“合拍”。

简谐振动的合成

简谐振动的合成

(A1 sin1 A2 sin2 )sint
合振幅
令： A1 cos1 A2 cos2 Acos 代入上式：
A1 sin1 A2 sin2 Asin
2
x ( A1 cos1 A2 cos2)cost (A1 sin1 A2 sin2 )sint
Acos cost Asin sint Acos(t ) x Acos(t )
x1(t) a cost
M aN
x2 (t) a cos(t ) x3(t) a cos(t 2 )
C
R N
A
a3
xN (t) a cos[t (N 1) ]O a1 P
在COM中：A 2R sin(N / 2)
上两式相除得：
在OCP中： a 2Rsin( / 2)
7
A a sin(N / 2) sin / 2
若 A1 A2, A 2A1
2.当 2 1 （2k 1） (k 0,1,2, ) 时,
A
A12
A
2 2
2 A1
A2
cos(
2
1
)
| A1 A2 | 合振动振幅最小。
若 A1 A2, A 0
A2
3.一般情况 | A1 A2 | A | A1 A2 |
5
A A2 A1
A2 A A1 A A1
第二节
简谐振动的合成
1
一、同方向同频率简谐振动的合成
在同一直线上同频率的两个简谐振
动分别为：
x1 A1 cos(t 1),
x2 A2 cos( t 2 )
• 代数方法： 振动合成
x x1 x2 A1 cos(t 1) A2 cos(t 2 )
(A1 cos1 A2 cos2) cost

同方向不同频率的简谐振动的合成

同方向不同频率的简谐振动的合成

同方向不同频率的简谐振动的合成好，今天咱们就来聊聊同方向不同频率的简谐振动合成。

别急，听我慢慢说，保证你一听就明白。

你得知道，简谐振动就像是一个物体在做上下左右那种规律性的摆动，感觉就像小孩子在秋千上摇来荡去那样，一来一回，一直不带停的。

你看过钟摆摆动吧？就那种感觉，越来越平稳，越过越规律，跟着一个固定的节奏跑。

但是，今天我们不光是讲单一的那种振动，我们要聊的可是两种频率不同的振动合成，它们在一起会怎么样呢？想象一下，两个人在同一个舞池跳舞，他们的舞步却不完全一致。

一个跳得慢，一个跳得快，开始的时候，大家还好像能勉强跟上，但过了一会儿，慢的那个开始觉得有点跟不上节奏，快的那个又有点等不及了。

是不是有点儿这种意思？没错，这就像两种不同频率的简谐振动，如果它们方向相同，但频率不同，合成出来的效果就有点复杂了。

你可以这样想：其中一个振动快得像飞一样，另一种则慢得像老牛拉破车，结果它们俩在同一个方向上“跑”来跑去。

它们的振动轨迹会不断交错，甚至会出现“合成振动”的现象，你可以理解成两者互相“纠缠”的结果。

要是它们的频率差别特别大，你会看到，快的那个有时候走得远了，慢的还在原地打转，合成的波形看上去就有点像一张波浪形的图，忽高忽低，像是过山车一样的刺激。

但是，有趣的地方就在这了！你看，两个不同频率的振动合成之后，它们的频率不单单是快的和慢的，而是产生了一种新的频率，这个频率叫做“合成频率”。

它就像是你听到两首歌，分别有各自的节奏，但一旦合并在一起，突然间你听到了一个新的旋律，乍一听挺陌生，但又有点儿奇妙的和谐感。

这个合成频率一般是由两种原始振动的频率差所影响的，也就是说，快的那个和慢的那个在一起后，调皮地产生了一种“中间”频率，所有的节奏似乎变得更有韵律了。

再说到合成的幅度，那更是有趣！幅度就像是你跳舞时的力度和气势。

你跳得越用力，别人就能感受到你那个震撼。

而在这两种不同频率的振动合成中，幅度也不是那么简单的加和，而是依赖于它们之间的相对位置。

第三十二讲：简谐振动的合成

第三十二讲：简谐振动的合成

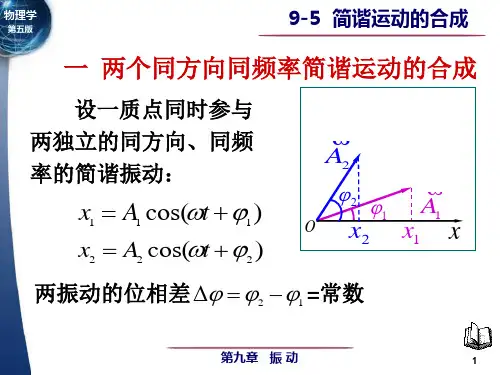
第三十二讲 §8.2 简谐振动的合成一、两个同方向同频率简谐振动的合成1、合振动仍然为简谐振动简谐振动1：()111cos ϕω+=t A x 简谐振动2：()222cos ϕω+=t A x合振动：()()()ϕωϕωϕω+=+++=+=t A t A t A x x x cos cos cos 2211212、合振动的振幅：()()22211222112sin sin cos cos A ϕϕϕϕA A A A +++=()1212212221sin sin cos cos 2ϕϕϕϕ+++=A A A A ()12212221cos 2ϕϕ-++=A A A A 3、合振动的初相位：22112211cos cos sin sin tan ϕϕϕϕϕA A A A ++==邻边对边 4、合振动的最大值，相长的条件：两分振动相位相同，相位差：() 3,2,1,0212=±=-=∆k k πϕϕϕ⇒()1cos 12=-ϕϕ ⇒ 212122212A A A A A A A +=++=5、合振动的最小值，相消的条件：两分振动相位相反，相位差：() 3,2,1,01212=+±=-=∆k k πϕϕϕ）（ ⇒()1cos 12-=-ϕϕ ⇒ 212122212A A A A A A A -=-+= 其他值：2121A A A A A +-练习题1. 一物体同时参与两个同方向的简谐振动：)212c o s (04.01π+π=t x (SI), )2cos(03.02π+π=t x (SI) 求此物体的振动方程．解：设合成运动（简谐振动）的振动方程为 )cos(φω+=t A x则 )c o s(2122122212φφ-++=A A A A A ①以 A 1 = 4 cm ，A 2 = 3 cm ，π=π-π=-212112φφ代入①式，得5cm 3422=+=A cm 2分又 22112211c o s c o s s i n s i n a r c t gφφφφφA A A A ++= ② ≈127°≈2.22 rad 2分 ∴)22.22cos(05.0+π=t x (SI) 1分练习题2. 两个同方向简谐振动的振动方程分别为 )4310cos(10521π+⨯=-t x (SI), )4110cos(10622π+⨯=-t x (SI) 求合振动方程．解：依合振动的振幅及初相公式可得φ∆++=c o s 2212221A A A A A 22210)4143cos(65265-⨯π-π⨯⨯⨯++= m 21081.7-⨯= m 2分)4/c o s (6)4/3c o s (5)4/s i n (6)4/3s i n (5a r c t gπ+ππ+π=φ = 84.8°=1.48 rad 2分则所求的合成振动方程为 )48.110cos(1081.72+⨯=-t x (SI)1分练习题3. 两个同方向的简谐振动的振动方程分别为x 1 = 4×10-2cos2π)81(+t (SI), x 2 = 3×10-2cos2π)41(+t (SI) 求合振动方程．解：由题意 x 1 = 4×10-2cos)42(π+πt (SI)x 2 =3×10-2cos)22(π+πt (SI) 按合成振动公式代入已知量，可得合振幅及初相为22210)4/2/cos(2434-⨯π-π++=A m= 6.48×10-2 m 2分)2/cos(3)4/cos(4)2/sin(3)4/sin(4arctgπ+ππ+π=φ=1.12 rad 2分 合振动方程为 x = 6.48×10-2 cos(2πt +1.12) (SI) 1分练习题4. 一质点同时参与两个同方向的简谐振动，其振动方程分别为 x 1 =5×10-2cos(4t + π/3) (SI) , x 2 =3×10-2sin(4t - π/6） (SI) 画出两振动的旋转矢量图，并求合振动的振动方程．解： x 2 = 3×10-2 sin(4t - π/6)= 3×10-2cos(4t - π/6- π/2)= 3×10-2cos(4t - 2π/3)．作两振动的旋转矢量图，如图所示． 图2分由图得：合振动的振幅和初相分别为A = (5-3)cm = 2 cm ，φ = π/3． 2分合振动方程为 x = 2×10-2cos(4t + π/3) (SI)1分小结：简谐振动的合成，与旋转矢量的解法作业：P33 8—16；8—17；预习：§8—2二、两个同方向不同频率简谐振动的合成 拍频三、相互垂直的简谐振动的合成1、同频率的相互垂直的简谐振动的合成2、不同频率的相互垂直的简谐振动的合成第三十二讲 §8.2 简谐振动的合成 8-16 解：设两质点的振动表达式分别为：)cos()cos(2211ϕωϕω+=+=t A x t A x 由图题可知，一质点在21A x =处时对应的相位为： 32/arccos 1πϕω==+A A t 同理：另一质点在相遇处时，对应的相位为：352/arccos2πϕω==+A A t 故相位差)()(12ϕωϕωϕ∆+-+=t t πππϕϕ3433512=-=-= 若21υυ与的方向与上述情况相反，故用同样的方法，可得：πππϕϕϕ∆32)3(312=--=-= 8-17 解：由图题8-17(图在课本上P 200)所示曲线可以看出，两个简谐振动的振幅相同，即m 05.021==A A ,周期均匀s 1.0=T ，因而圆频率为：ππω202==T 由x -t 曲线可知，简谐振动1在t=0时，,010=x 且010>υ，故可求得振动1的初位相πϕ2310=. 同样，简谐振动2在t=0时，πϕυ==-=202020,0,05.0可知m x 故简谐振动1、2的振动表达式分别为： mt x t x )20cos(05.0)2320cos(05.021ππππ+=+=因此，合振动的振幅和初相位分别为：m A A A A A 210202122211025)cos(2-⨯=-++=ϕϕ 2021012021010cos cos sin sin arctan ϕϕϕϕϕA A A A ++= ππ4541a r c t a n 或== 但由x-t 曲线知，t=0时，πϕ45,05.021应取因此-=+=x x x . 故合振动的振动表达式：m t x )4520cos(10252ππ+⨯=-习题8-16图。

简谐振动的合成

简谐振动的合成
8.2 简谐振动的合成
一、同方向、同频率谐振动的合成 质点同时参与两个同方向同频率的谐振动:
x1(t) A1 cos(t 1)
A
x2 (t) A2 cos(t 2 )
A2
x x1 x2 Acos(t )
A A12 A22 2A1A2 cos(2 1) 2
tg A1 sin1 A2 sin2
1 2
r A
X
合振动初相位
1 2
两分振动相互加强
A1 X A2
o
x=x1+x2
t
A A12 A22 2A1 A2 cos(2 1 )
若两分振动反相位：
2 1 (2k 1) k 0,1, 2, r
合振幅最小
r A1
A A1 A2 合振动初相位
r 2 A
A2 o
1
X
若A1>A2 1 若A1<A2 2
A1 cos1 A2rcos2
O
1
x2
A1
x1
x
x
结论 ①合矢量 A即为合振动所对应的旋转矢量。
②合振动仍为简谐振动，振动角频率仍为ω。
分析 A A12 A22 2A1 A2 cos(2 1 )
若两分振动同相位：
2 1 2k k 0,1, 2,
合振幅最大
A A1 A2
o
r
A2
r
A1
4
求合振动的振动方程。
解：
2
T
20
x(cm) 5
x1 x2
A1 A2 5cm
0.1
o 0.05
且 t 时0
-5
r
A2
x10 0, v10 f 0; x20 5cm

简谐振动合成与分解

简谐振动合成与分解
意义
通过将复杂振动分解为简单的简谐振动，可以更好地理解和分析振动的本质。
实际应用中的振动分解
信号处理
在信号处理领域，傅里叶变换被 广泛应用于将时域信号转换为频 域信号，从而分析信号的频率成 分。
机械振动分析
在机械工程中，通过对机械振动 的分析，可以了解机械系统的动 态特性和振动规律，为优化设计 提供依据。
实验验证与实际应用
未来可以通过实验验证和实际应用来 检验简谐振动合成与分解的理论，推 动其在解决实际问题中的应用。
THANKS
感谢观看
ERA
两个同频率简谐振动的合成
合成结果仍为同频率简谐振动，振幅 和相位由两个简谐振动的振幅和相位 决定。
当两个简谐振动的相位差为0或π时，合 成振动的振幅为两者之和；相位差为 π/2或3π/2时，合成振动的振幅为两者 之差。
两个不同频率简谐振动的合成
合成结果为非简谐振动，其频率为两个简谐振动频率的线性 组合。
地震学
在地震学中，通过分析地震波的 频谱，可以研究地球内部的结构 和性质。
04
合成与分解的应用
BIG DATA EMPOWERS TO CREATE A NEW
ERA
在物理学中的应用
01
波动合成
简谐振动合成与分解是研究波动 的重要基础，如声波、光波等的 合成与分解。
电磁波
02
03
原子振动
电磁波的合成与分解是研究电磁 波性质的关键，如无线电波、可 见光等。
能量守恒
简谐振动的能量是守恒的， 即振幅不变。
简谐振动的表示方法
三角函数表示法
简谐振动的位移、速度和加速度可以用三角函数来表示，如正弦函数或余弦函 数。
相图表示法

一同频率同一直线上的简谐振动的合成

一同频率同一直线上的简谐振动的合成
§4.4 简谐振动的合成
一.同频率、同一直线上的简谐振动的合成 分振动：x1 =A1cos( t+1 ) x2 =A2cos( t+2 )
合振动： x= x1+x2 = Acos( t+ )
A A1 A2 2 A1 A2cos( 2 1 )
2
2
A1sin1 A2sin 2 tg A1cos1 A2cos 2
x y 2 1 2 A1 A2
y
2
2
合振动不再是谐振动。
y
x
x 左旋
右旋
2 -1=/2
2 -1=-/2
21
两个频率相同、 振幅不同的互
相垂直简谐
Δ=0 Δ=/4 Δ=/2 Δ=3/4
振动的合成
Δ=
Δ=5/4
Δ=3/2
Δ=7/4
22
四.不同频率垂直谐振动的合成 李萨如图形 x =A1cos(1 t+1 ) y =A2cos(2 t+2 )
2， = 0 （临介阻尼）
x e t C1 C 2 t
3， < 0 （欠阻尼）
xe
e
t
t
C cos
1
C e
1
i 0 2 2 t
C2 e
2
i 0 2 2 t

2 2
0 t C2 sin 0 t
2
2 2

( 2 1 )

2
o
x
10
例题4.17 求同方向、同频率、同振幅、依次间相 位差均为的N个谐振动的合振动方程。 光的衍射 解
选择适当的计时起点，使某个简谐振动的初 相为零，则有
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
采用旋转矢 量法，可直观 地领会简谐振 动表达式中各 个物理量的意 义。
A 的长度
振幅A
ω
M
A
A旋转的角速度
振动圆频率 O
t 0
P
X
x
A 旋转的方向
逆时针方向
A 与参考方向x 的夹角 振动相位
M 点在 x 轴上投影(P点)的运动规律：
x Acos(t 0 )
旋转矢量
x Acos t
返回10
四、简谐振动的能量
k
m
k m
0
x
X
m2 k
势能
Ep
1 kx2 2
1 2
kA2
cos2 ( t
)
动能
Ek
1 mv2 2
1 mkA22A2
2
sin 2
t
E
Ek
Ep
1 kA2 2
1mm 2 A2
2
惯性质量
单摆的能量
LC 电路 的能量
能量随空间变化
能量随时间变化
E
x
E
E
E p Ek
A
Ep
xA
6
a 0.12 2 cos 1.03m / s 2
6
返回10
（3）第一次通过平衡位置的时刻。
x
At
平衡 位置
A0 At
振幅矢量旋转角度 5 32 6
A0 问题转化为：已知旋转2需要T 时
间，问旋转 5 /6 需要多少时间？
2 5 / 6
T2
t
t 5 0.83s 6
还可以求“第二次……”——旋转角度11 /6
ax
X
X
O
1
2
A1
A2
两个同频率的简谐运动：
相位之差为 采用旋转矢量直观表示为：
(t 2 ) (t 1) 2 1. x2 A2 cos(t 2 ) x1 A1 cos(t 1)
x
A1
t
A2
t
x
A1
A2
同相
t
x
x
A1
A1t A2 t
A2
反相
t
例题1
已知简谐振动表达
x0
mg k
物体受的合力：
x
x0
0
x
FR mg k(x0 x) k x
x 2x 0 2 k g
m x0
T 2
f
mg
x0 g
例、单摆
1、细线质量不计
约 定 2、 50 sin
0
3、阻力不计
质点 m 受力如图重力矩：M mgl sin mgl
l
根据质点的动量距定理 dL M
t
1
0
t
2
ቤተ መጻሕፍቲ ባይዱ
1 A2
a 2 Acos t x(t)
t
1
0
t
2
例：物体的质量为 m , 弹簧的劲
度系数为 k 。其静止变形 x0
手拉物体后无初速地释放，确定物
体的运动规律 。
l0
建立如图坐标系，以平衡位置为坐标 原点。物体坐标为 x , 所受的弹性回 复力为 f 和重力 mg
在平衡位置处 mg k x0 0
研究目的 —— 利用、减弱 或 消除
§2.1 简谐振动
一、描述简谐振动的特征量
质量可忽略的弹簧，一 端固定，一端系一有质 量的物体，称此系统为 弹簧振子。
建 立 如 图的 坐 标系 物 体 质 量 m, 坐 标 x 所 受 回 复 力 为 F.
令 k
m
k
Fm
0
F kx
d2x F m
dt 2
x
X
d2x k x0
dt 2 m
d2x dt 2
2
x
0
此方程的通解为： x A cost
xt A cost
• 物理量随时间的变化规律可以用正弦、余弦函 数描述，称之为简谐振动。
上式称之为 简谐 振 动表 达式（简谐函数或振动方程）
d2x dt 2
2
x
0
简谐振动的动力学特征方程
F kx 简谐振动的动力学条件
x Acos(t 2 )
3
试画出振动曲线
x
x
A
2
3
t
0
A(0)
例题2
一质点沿x 轴作简谐运动，A = 0.12 m ，T=2s ，当t = 0
时质点在平衡位置的位移 x0 = 0.0 6m 向x 轴正向运动。
求：（1）简谐运动表达式；
（2）t =T/4 时，质点的位置、速度、加速度；
（3）第一次通过平衡位置的时刻。
dt
T
d 2
dt 2
g
l
0
摆角在作简谐振动
m
0 cos t 0
mg
？ 固有
园频率
g 设初始条件 0 振幅和
l
v0 0 初相=
3. 简谐振动的矢量图示法
旋转矢量:一长度等于振幅A 的矢量 在A纸平面内
绕O点沿逆时针方向旋转，其角速度与谐振动的角频 率相等，这个矢量称为旋转矢量。
2
a
d2x dt 2
A 2
cost
简谐振动的各 阶导数也都作 简谐振动
am cos(t ) x 2
简谐振动的运动学特征方程
三、 振 动 曲 线 旋转矢量
1. 振 动 曲 线
A1 1
x Acos t x(t)
t
0
0.5
1
1.5
2
-A1 1 0
t
2
1 A
v Asin t x(t)
谐振动的特征量
1、 A 振幅
2、 T 周期
1
T
频率
x Acos t Acos (t T )
T 2 2 m
k
2
圆频率又称 固有圆频率
3、 t 相位 初相位
确定物体振动状态的物理量
二 、简谐运动的速度和加速度
xt Acos t
v dx A sint
dt
A cos t
§2-1 简谐振动 §2-2 简谐振动的合成 §2-3 波的描述 §2-4波的衍射和干涉 §2-5声波及超声波的生物效应
广义：物理量在某一定值附近反复变化即为振动。
周期振动：物理量每隔一固定的时间间隔其数值重复一次
x(t) x(t T )
振动频率
1
T
机械振动：物体在某一位置附近往复运动
复杂振动 = 若干个简谐振动的合成
x
x
A0
A
t+ 相位
1
t
At
x( t )
0
振幅矢量
1
0
t
2
绕O点以角速度 逆时针旋转的矢量At ，
在x 轴上的投影正好描述了一个简谐振动。
v0 O
X
A
X
av,
v0 O
A
速度、加速度的旋转矢量表示法：
v
A
a t 0
沿X 轴的投 影为简谐运动的速度、
M
加速度表达式。
vx
M 点:vm A am 2 A
X
E p Ek t
胡玉才：e-mail
hyc@
五、阻尼振动 受迫振动 共振
1.阻尼振动
振动物体不受任何阻力的影响，只在回复力作用下 所作的振动，称为无阻尼自由振动。
在回复力和阻力作用下的振动称为阻尼振动。
阻尼：消耗振动系统能量的原因。
解： （1） xx 0A.1c2ocsost t
x
x
3
3
＝ 2T?
A/2
t
０
（2）t =T/4 时，质点的位置、速度、加速度；
x 0.12cos t
v
0.12
sin
t
3
a
0.12
2
cos
t
3
3
tT 1 42
x 0.12cos 1.04m
2 3
v 0.12 sin 0.189m / s