两个简谐振动的合成

云南大学软件学院 实验报告课程： 大学物理实验 学期： 任课教师： 班级： = 学号： == 序号： = 姓名： = 成绩：实验6 简谐振动的合成内容一 同方向同频率简谐振动的合成两个简谐振动的方程为使用matlab 编写程序，求x1,x2,合振动的波形，讨论相位差对合成振动的影响。

相位差至少讨论4中情况（1.为0°;2.为180°；3.小于180°；4.大于180°），要求所有波形画在同一个figure 中。

()()⎩⎨⎧+=+=222111cos cos ϕωϕωt A x t A x内容二 相互垂直方向同频率简谐振动的合成两个简谐振动的方程为使用matlab 编写程序，求x,y,合振动的波形，讨论相位差对合成振动的影响。

相位差至少讨论4中情况（1.为0°;2.为180°；3.小于180°；4.大于180°），要求所有波形画在同一个figure 中。

()()⎩⎨⎧+=+=y y x x t A y t A x ϕωϕωcos cos内容三相互垂直方向不同频率简谐振动的合成(李萨如图形) 使用matlab编写程序，画李萨如图形，要求：1.至少4种频率比2.至少8种相位差3.所有图形画在同一个figure中，添加标注。

如：cleart = 0:0.01:4;Ax = 1;Ay = 3;w1 = 1; w2 = 1./2;w3 = 2./3;w4 = 3./4;w5 = 2./5;m0 = 0;m1 = 0;m2 = pi./4;m3 = pi./2;m4 = 3.*pi./4;m5 = pi;m6 = 5.*pi./4; m7 =3.*pi./2;m8 = 7.*pi./4; x0 = Ax.*cos(2.*pi*t+m0);y11 = Ay.*cos(2.*w1.*pi*t+m1);y12 = Ay.*cos(2.*w1.*pi*t+m2);y13 = Ay.*cos(2.*w1.*pi*t+m3);y14 = Ay.*cos(2.*w1.*pi*t+m4);y15 = Ay.*cos(2.*w1.*pi*t+m5);y16 = Ay.*cos(2.*w1.*pi*t+m6);y17 = Ay.*cos(2.*w1.*pi*t+m7);y18 = Ay.*cos(2.*w1.*pi*t+m8);y21 = Ay.*cos(2.*w2.*pi*t+m1);y22 = Ay.*cos(2.*w2.*pi*t+m2);y23 = Ay.*cos(2.*w2.*pi*t+m3);y24 = Ay.*cos(2.*w2.*pi*t+m4);y25 = Ay.*cos(2.*w2.*pi*t+m5);y26 = Ay.*cos(2.*w2.*pi*t+m6);y27 = Ay.*cos(2.*w2.*pi*t+m7);y28 = Ay.*cos(2.*w2.*pi*t+m8);y31 = Ay.*cos(2.*w3.*pi*t+m1);y32 = Ay.*cos(2.*w3.*pi*t+m2);y33 = Ay.*cos(2.*w3.*pi*t+m3);y34 = Ay.*cos(2.*w3.*pi*t+m4);y35 = Ay.*cos(2.*w3.*pi*t+m5);y36 = Ay.*cos(2.*w3.*pi*t+m6);y37 = Ay.*cos(2.*w3.*pi*t+m7);y38 = Ay.*cos(2.*w3.*pi*t+m8);y41 = Ay.*cos(2.*w4.*pi*t+m1);y42 = Ay.*cos(2.*w4.*pi*t+m2);y43 = Ay.*cos(2.*w4.*pi*t+m3);y44 = Ay.*cos(2.*w4.*pi*t+m4);y45 = Ay.*cos(2.*w4.*pi*t+m5);y46 = Ay.*cos(2.*w4.*pi*t+m6);y47 = Ay.*cos(2.*w4.*pi*t+m7);y48 = Ay.*cos(2.*w4.*pi*t+m8);y51 = Ay.*cos(2.*w5.*pi*t+m1);y52 = Ay.*cos(2.*w5.*pi*t+m2);y53 = Ay.*cos(2.*w5.*pi*t+m3);y54 = Ay.*cos(2.*w5.*pi*t+m4);y55 = Ay.*cos(2.*w5.*pi*t+m5);y56 = Ay.*cos(2.*w5.*pi*t+m6);y57 = Ay.*cos(2.*w5.*pi*t+m7);y58 = Ay.*cos(2.*w5.*pi*t+m8);subplot(5,8,1);plot(x0,y11);Axis([-4 4 -4 4]);text(-16,0,'ω =1');text(-2,7,'0');text(-16,7,'相位差');subplot(5,8,2);plot(x0,y12);Axis([-4 4 -4 4]);text(-2,7,'π/4'); subplot(5,8,3);plot(x0,y13);Axis([-4 4 -4 4]);text(-2,7,'π/2'); subplot(5,8,4);plot(x0,y14);Axis([-4 4 -4 4]);text(-2,7,'3π/4'); subplot(5,8,5);plot(x0,y15);Axis([-4 4 -4 4]);text(-2,7,'π');subplot(5,8,6);plot(x0,y16);Axis([-4 4 -4 4]);text(-2,7,'5π/4'); subplot(5,8,7);plot(x0,y17);Axis([-4 4 -4 4]);text(-2,7,'3π/2'); subplot(5,8,8);plot(x0,y18);Axis([-4 4 -4 4]);text(-2,7,'7π/4'); subplot(5,8,9);plot(x0,y21);Axis([-4 4 -4 4]);text(-16,0,'ω = 1/2'); subplot(5,8,10);plot(x0,y22);Axis([-4 4 -4 4]);subplot(5,8,11);plot(x0,y23);Axis([-4 4 -4 4]);subplot(5,8,12);plot(x0,y24);Axis([-4 4 -4 4]);subplot(5,8,13);plot(x0,y25);Axis([-4 4 -4 4]);subplot(5,8,14);plot(x0,y26);Axis([-4 4 -4 4]);subplot(5,8,15);plot(x0,y27);Axis([-4 4 -4 4]);subplot(5,8,16);plot(x0,y28);Axis([-4 4 -4 4]);subplot(5,8,17);plot(x0,y31);Axis([-4 4 -4 4]);text(-16,0,'ω = 2/3'); subplot(5,8,18);plot(x0,y32);Axis([-4 4 -4 4]);subplot(5,8,19);plot(x0,y33);Axis([-4 4 -4 4]);subplot(5,8,20);plot(x0,y34);Axis([-4 4 -4 4]);subplot(5,8,21);plot(x0,y35);Axis([-4 4 -4 4]);subplot(5,8,22);plot(x0,y36);Axis([-4 4 -4 4]);subplot(5,8,23);plot(x0,y37);Axis([-4 4 -4 4]);subplot(5,8,24);plot(x0,y38);Axis([-4 4 -4 4]);subplot(5,8,25);plot(x0,y41);Axis([-4 4 -4 4]);text(-16,0,'ω = 3/4'); subplot(5,8,26);plot(x0,y42);Axis([-4 4 -4 4]);subplot(5,8,27);plot(x0,y43);Axis([-4 4 -4 4]);subplot(5,8,28);plot(x0,y44);Axis([-4 4 -4 4]);subplot(5,8,29);plot(x0,y45);Axis([-4 4 -4 4]);subplot(5,8,30);plot(x0,y46);Axis([-4 4 -4 4]);subplot(5,8,31);plot(x0,y47);Axis([-4 4 -4 4]);subplot(5,8,32);plot(x0,y48);Axis([-4 4 -4 4]);subplot(5,8,33);plot(x0,y51);Axis([-4 4 -4 4]);text(-16,0,'ω = 2/5'); subplot(5,8,34);plot(x0,y52);Axis([-4 4 -4 4]);subplot(5,8,35);plot(x0,y53);Axis([-4 4 -4 4]);subplot(5,8,36);plot(x0,y54);Axis([-4 4 -4 4]);subplot(5,8,37);plot(x0,y55);Axis([-4 4 -4 4]);subplot(5,8,38);plot(x0,y56);Axis([-4 4 -4 4]);subplot(5,8,39);plot(x0,y57);Axis([-4 4 -4 4]);subplot(5,8,40);plot(x0,y58);Axis([-4 4 -4 4]);。

©物理系_2015_09《大学物理AII 》作业 No.01 机械振动班级 ________ 学号 ________ 姓名 _________ 成绩 _______一、 判断题：（用“T ”表示正确和“F ”表示错误）1/3/5 2 4[ F ] 1．只有受弹性力作用的物体才能做简谐振动。

解：如单摆在作小角度摆动的时候也是简谐振动，其回复力为重力的分力。

[ F ] 2．简谐振动系统的角频率由振动系统的初始条件决定。

解：P5. 根据简谐振子角频率公式mk=ω，可知角频率是一个完全由振动系统本身性质决定的常量，与初始条件无关。

我们也将角频率称为固有角频率。

[ F ] 3．单摆的运动就是简谐振动。

解：P14-15 单摆小角度的摆动才可看做是简谐振动。

[ T ] 4．孤立简谐振动系统的动能与势能反相变化。

解：P9 孤立的谐振系统 机械能守恒，动能势能反相变化。

[ F ] 5．两个简谐振动的合成振动一定是简谐振动。

解: 同向不同频率的简谐振动的合成结果就不一定是简谐振动。

总结：1、3、5小题均为简谐振动的定义性判断.简谐运动是最基本也是最简单的一种机械振动。

当某物体进行简谐运动时，物体所受的力跟位移成正比，并且力总是指向平衡位置。

二、选择题：1. 把单摆从平衡位置拉开，使摆线与竖直方向成一微小角度θ，然后由静止放手任其振动，从放手时开始计时。

若用余弦函数表示其运动方程，则该单摆振动的初相位为[ C ] (A) θ; (B) π23; (C) 0; (D) π21。

解：对于小角度摆动的单摆，可以视为简谐振动，其运动方程为：()()0cos ϕωθθ+=t t m ，根据题意，t = 0时，摆角处于正最大处，θθ=m，即：01cos cos 0000=⇒=⇒==ϕϕθϕθθ。

类似公式： ()()0cos ϕω+=t A t x2．一个简谐振动系统，如果振子质量和振幅都加倍，振动周期将是原来的 [D] (A) 4倍(B) 8倍(C) 2倍(D)2倍解： P5 公式(12.1.8) m T k m T m k T ∝⇒=⇒⎪⎭⎪⎬⎫==/2/2πωωπ,所以选D 。

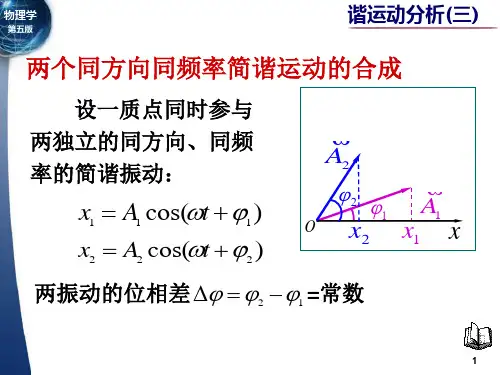
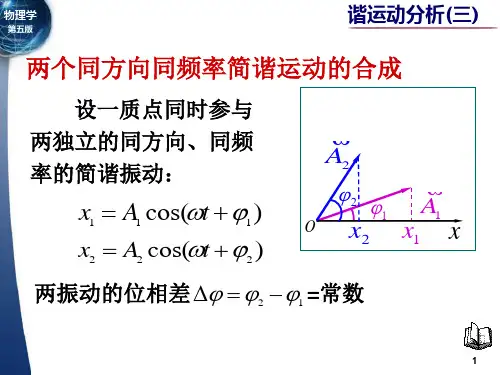
大学物理学——振动和波振 动班级 学号 姓名 成绩内容提要1、简谐振动的三个判据（1）；（2）；（3）2、描述简谐振动的特征量： A 、T 、γ；T1=γ，πγπω22==T3、简谐振动的描述：（1）公式法 ；（2）图像法；（3）旋转矢量法4、简谐振动的速度和加速度：)2cos()sin(v00πϕωϕωω++=+-==t v t A dt dx m ； a=）（）（πϕωϕωω±+=+=0m 0222t a t cos -dtxd A 5、振动的相位随时间变化的关系：6、简谐振动实例弹簧振子：，单摆小角度振动：，复摆：0mgh dt d 22=+θθJ ,T=2mghJπ 7、简谐振动的能量：222m 21k 21A A Eω==系统的动能为：）（ϕωω+==t sin m 21mv 212222A E K ；系统的势能为：）ϕω+==t (cos k 21kx 21222A E P8、两个简谐振动的合成（1）两个同方向同频率的简谐振动的合成合振动方程为：）（ϕω+=t cos x A 其中，其中；。

＊(2) 两个同方向不同频率简谐振动的合成拍：当频率较大而频率之差很小的两个同方向简谐运动合成时，其合振动的振幅表现为时而加强时而减弱的现象，拍频：12-γγγ=＊（3）两个相互垂直简谐振动的合成合振动方程：）（1221221222212-sin )(cos xy 2y x ϕϕϕϕ=--+A A A A ，为椭圆方程。

练习一一、 填空题1．一劲度系数为k 的轻弹簧，下端挂一质量为m 的物体，系统的振动周期为T 1。

若将此弹簧截去一半的长度，下端挂一质量为m/2的物体，则系统的周期T 2等于 。

2．一简谐振动用余弦函数表示，其振动曲线如图所示，则此简谐振动的三个特征量为：A ＝ ；=ω ;=ϕ 。

3．如图，一长为l 的均匀细棒悬于通过其一端的光滑水平固定轴上，做成一复摆。

已知细棒绕过其一端的轴的转动惯量J ＝3/2ml ，此摆作微小振动的周期为 。

第九章基本知识小结⒈物体在线性回复力F = - kx ，或线性回复力矩τ= - c φ作用下的运动就是简谐振动，其动力学方程为 ,02022=+x dt x d ω（x 表示线位移或角位移）；弹簧振子：ω02=k/m ，单摆：ω02=g/l ，扭摆：ω02=C/I.⒉简谐振动的运动学方程为 x = Acos(ω0t+α)；圆频率、频率、周期是由振动系统本身决定的，ω0=2π/T=2πv ；振幅A 和初相α由初始条件决定。

⒊在简谐振动中，动能和势能互相转换，总机械能保持不变；对于弹簧振子，22021221A m kA E E p k ω==+。

⒋两个简谐振动的合成⒌阻尼振动的动力学方程为 022022=++x dt dx dtx d ωβ。

其运动学方程分三种情况：⑴在弱阻尼状态（β＜ω0），振动的方向变化有周期性，220'),'cos(βωωαωβ-=+=-t Ae x t ，对数减缩 = βT ’.⑵在过阻尼状态（β＞ω0），无周期性，振子单调、缓慢地回到平衡位置。

⑶临界阻尼状态（β=ω0），无周期性，振子单调、迅速地回到平衡位置⒍受迫振动动力学方程 t f x dt dx dt x d ωωβcos202022=++； 其稳定解为 )cos(0ϕω+=t A x ，ω是驱动力的频率，A 0和φ也不是由初始条件决定,222220004)(/ωβωω+-=f A 2202ωωβωϕ--=tg 当2202βωω-=时，发生位移共振。

9.2.1 一刚体可绕水平轴摆动。

已知刚体质量为m ，其重心C 和轴O 间的距离为h ，刚体对转动轴线的转动惯量为I 。

问刚体围绕平衡位置的微小摆动是否是简谐振动？如果是，求固有频率，不计一切阻力。

解：规定转轴正方向垂直纸面向外，忽略一切阻力，则刚体所受力矩τ= - mghsin φ因为是微小摆动，sin φ≈φ,∴τ= - mgh φ，即刚体是在一线性回复力矩作用下在平衡位置附近运动，因而是简谐振动。

第三十二讲 §8.2 简谐振动的合成一、两个同方向同频率简谐振动的合成1、合振动仍然为简谐振动简谐振动1：()111cos ϕω+=t A x 简谐振动2：()222cos ϕω+=t A x合振动：()()()ϕωϕωϕω+=+++=+=t A t A t A x x x cos cos cos 2211212、合振动的振幅：()()22211222112sin sin cos cos A ϕϕϕϕA A A A +++=()1212212221sin sin cos cos 2ϕϕϕϕ+++=A A A A ()12212221cos 2ϕϕ-++=A A A A 3、合振动的初相位：22112211cos cos sin sin tan ϕϕϕϕϕA A A A ++==邻边对边 4、合振动的最大值，相长的条件：两分振动相位相同，相位差：() 3,2,1,0212=±=-=∆k k πϕϕϕ⇒()1cos 12=-ϕϕ ⇒ 212122212A A A A A A A +=++=5、合振动的最小值，相消的条件：两分振动相位相反，相位差：() 3,2,1,01212=+±=-=∆k k πϕϕϕ）（ ⇒()1cos 12-=-ϕϕ ⇒ 212122212A A A A A A A -=-+= 其他值：2121A A A A A +-练习题1. 一物体同时参与两个同方向的简谐振动：)212c o s (04.01π+π=t x (SI), )2cos(03.02π+π=t x (SI) 求此物体的振动方程．解：设合成运动（简谐振动）的振动方程为 )cos(φω+=t A x则 )c o s(2122122212φφ-++=A A A A A ①以 A 1 = 4 cm ，A 2 = 3 cm ，π=π-π=-212112φφ代入①式，得5cm 3422=+=A cm 2分又 22112211c o s c o s s i n s i n a r c t gφφφφφA A A A ++= ② ≈127°≈2.22 rad 2分 ∴)22.22cos(05.0+π=t x (SI) 1分练习题2. 两个同方向简谐振动的振动方程分别为 )4310cos(10521π+⨯=-t x (SI), )4110cos(10622π+⨯=-t x (SI) 求合振动方程．解：依合振动的振幅及初相公式可得φ∆++=c o s 2212221A A A A A 22210)4143cos(65265-⨯π-π⨯⨯⨯++= m 21081.7-⨯= m 2分)4/c o s (6)4/3c o s (5)4/s i n (6)4/3s i n (5a r c t gπ+ππ+π=φ = 84.8°=1.48 rad 2分则所求的合成振动方程为 )48.110cos(1081.72+⨯=-t x (SI)1分练习题3. 两个同方向的简谐振动的振动方程分别为x 1 = 4×10-2cos2π)81(+t (SI), x 2 = 3×10-2cos2π)41(+t (SI) 求合振动方程．解：由题意 x 1 = 4×10-2cos)42(π+πt (SI)x 2 =3×10-2cos)22(π+πt (SI) 按合成振动公式代入已知量，可得合振幅及初相为22210)4/2/cos(2434-⨯π-π++=A m= 6.48×10-2 m 2分)2/cos(3)4/cos(4)2/sin(3)4/sin(4arctgπ+ππ+π=φ=1.12 rad 2分 合振动方程为 x = 6.48×10-2 cos(2πt +1.12) (SI) 1分练习题4. 一质点同时参与两个同方向的简谐振动，其振动方程分别为 x 1 =5×10-2cos(4t + π/3) (SI) , x 2 =3×10-2sin(4t - π/6） (SI) 画出两振动的旋转矢量图，并求合振动的振动方程．解： x 2 = 3×10-2 sin(4t - π/6)= 3×10-2cos(4t - π/6- π/2)= 3×10-2cos(4t - 2π/3)．作两振动的旋转矢量图，如图所示． 图2分由图得：合振动的振幅和初相分别为A = (5-3)cm = 2 cm ，φ = π/3． 2分合振动方程为 x = 2×10-2cos(4t + π/3) (SI)1分小结：简谐振动的合成，与旋转矢量的解法作业：P33 8—16；8—17；预习：§8—2二、两个同方向不同频率简谐振动的合成 拍频三、相互垂直的简谐振动的合成1、同频率的相互垂直的简谐振动的合成2、不同频率的相互垂直的简谐振动的合成第三十二讲 §8.2 简谐振动的合成 8-16 解：设两质点的振动表达式分别为：)cos()cos(2211ϕωϕω+=+=t A x t A x 由图题可知，一质点在21A x =处时对应的相位为： 32/arccos 1πϕω==+A A t 同理：另一质点在相遇处时，对应的相位为：352/arccos2πϕω==+A A t 故相位差)()(12ϕωϕωϕ∆+-+=t t πππϕϕ3433512=-=-= 若21υυ与的方向与上述情况相反，故用同样的方法，可得：πππϕϕϕ∆32)3(312=--=-= 8-17 解：由图题8-17(图在课本上P 200)所示曲线可以看出，两个简谐振动的振幅相同，即m 05.021==A A ,周期均匀s 1.0=T ，因而圆频率为：ππω202==T 由x -t 曲线可知，简谐振动1在t=0时，,010=x 且010>υ，故可求得振动1的初位相πϕ2310=. 同样，简谐振动2在t=0时，πϕυ==-=202020,0,05.0可知m x 故简谐振动1、2的振动表达式分别为： mt x t x )20cos(05.0)2320cos(05.021ππππ+=+=因此，合振动的振幅和初相位分别为：m A A A A A 210202122211025)cos(2-⨯=-++=ϕϕ 2021012021010cos cos sin sin arctan ϕϕϕϕϕA A A A ++= ππ4541a r c t a n 或== 但由x-t 曲线知，t=0时，πϕ45,05.021应取因此-=+=x x x . 故合振动的振动表达式：m t x )4520cos(10252ππ+⨯=-习题8-16图。

三角函数法对同方向同频率简谐振动合成的求解
同方向同频率简谐振动是指两个物体以相同的角频率且方向一致地做简谐振动。

这种振动常常出现在机械振动、波动和电磁振动等领域中。

因此，对同方向同频率简谐振动的合成求解是很重要的。

三角函数法是求解简谐振动合成问题的常用方法，它利用三角函数的性质，将振动方程表示为三角函数的形式，从而方便进行进一步的计算。

下面我们将介绍三角函数法对同方向同频率简谐振动合成的求解步骤。

（1）假设两个物体分别做简谐振动，振幅为A1和A2，初始相位分别为φ1和φ2，角频率均为ω。

（2）写出两个物体的振动方程：
x1 = A1sin(ωt + φ1)
（4）根据三角函数的和差公式，将上式化简为：
x = [A1cos(φ1) + A2cos(φ2)]sin(ωt) + [A1sin(φ1) + A2sin(φ2)]cos(ωt)（6）求出两个简谐振动的振幅和相位，即可求出合成振动的振幅和相位。

振幅：
相位：
（7）利用上式求出合成振动的振幅和相位后，可以得到合成振动的振动方程：
其中，A为合成振动的振幅，φ为合成振动的相位，ω为角频率，t为时间。