同方向的简谐振动的合成

电子技术与软件工程Electronic Technology & Software Engineering电子技术Electronic Technology 同方向同频率简谐振动合成问题求解方法的研究贾冬梅（中北大学信息商务学院山西省晋中市030600 ）摘要：本文分别运用解析法和旋转矢量法来求解两个同方向同频率简谐振动的合成问题并分析总结了它们冬自的特点.通过对比发 现：运用旋转矢量法比解析法更为直观有效，它可以生免去对物理公式的记忆和复杂的数学计算.但是在一般情形下，运用解析法求解更为有效.对于合振动初相位的确定，运用旋转矢量法比解析法更加直观、有效和便捷.关键词：振动合成；解析法；旋转矢量法；振幅；初相简谐振动是机械振动中最简单、最基本的振动形式，任何复杂 的振动都可以看作是简谐振动的合成旳。

而同方向同频率的简谐振 动的合成又是简谐振动的合成中最简单最重要的形式，它为波干涉 和衍射现象的分析奠定了理论基础，因此研究同方向同频率简谐振 动的合成有着十分重要的意义。

寻求一种高效便捷的求解简谐振动 合振动的振动的方法成为了解决同方向同频率简谐振动的合成的关 键3」。

对于同方向同频率简谐振动的合成问题，大学物理教材中 常使用旋转矢量法和解析法来进行讨论分析‘网。

下面分别运用解 析法和旋转矢量法来求解同方向同频率简谐振动合成问题，分析总 结它们各自的特点，为这类问题的分析和求解提供一些参考和借鉴。

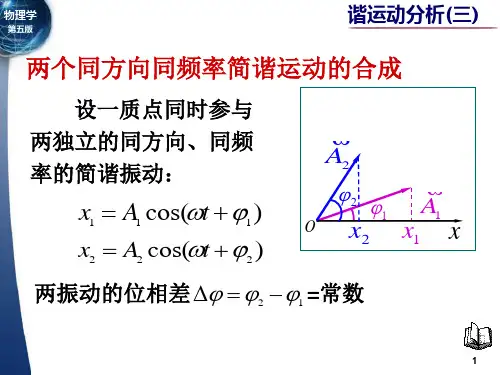
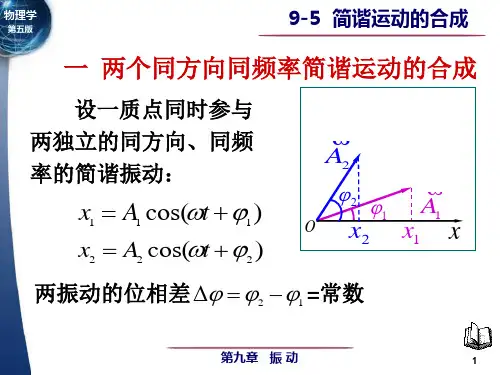
1两个同方向同频率简谐振动的合成设两个简谐振动都沿着x 轴方向振动，平衡位置都为坐标原点， 它们振动的角频率3,振幅分别为A]和A2，初相分别为®和％， 它们的振动方程分别为：x,=A| cos （（ot+（p]） x 2=A 2 cos （（ot+（p 2）求这两个解析振动的合振动。

1. 1解析法由于两个简谐振动都沿着X 轴方向振动，所以这两个简谐振动在任一时刻合振动的位移也应在X 轴方向上，且合振动的位移X 等 于这两个分振动位移的代数和，即：X=X]+x 2将分振动的方程X1和X2代入上式展开整理：x = x }+x 2= A } COS （＜zX + % ） + 厦2 COS （m + 02 ）=4 cos （p 、cos - /1] sin （p } cos cotA 2 cos （p 2 cos cot- A 2s\n （p 2 sin cut=（A, cos （p 、+ A 2 cos %） cos cot sin （p 、4- A 2 sin （p 2） sin cot 令 A cos （p=A] cos （p]+A 2 cos （p 2 A sin （p=A 1 sin （P]+A 2 sin （p 2 得至lj x=A cos （p coscot-A sin （p sin （ot=A cos （（ot+（p ）这一结果表明：两个同方向同频率简谐振动的合振动依旧是一 个简谐振动，且合振动的频率与分振动的频率相同都等于3,合振 动的振幅和初相可以表示为：A = J （/sin 0）2 +（/cos （p ）2=J A ： + / j + 2A t A 2 cos （02 - ％）川 sin 0 _ A x sin ® + A 2 sin （p 2t a n （p =------—-------------------A cos （p A x cos （p 、+ A 2 cos （p 21.2旋转矢量法如图1所示，4和力2分别为两个分振动的旋转矢量，它们以相 同的角速度绕o 点做逆时针转动，t=Os 时它们与x 轴正向的夹角分 别为卩和①。

三角函数法对同方向同频率简谐振动合成的求解简谐振动是物理学中常见的一种运动形式，它具有周期性、振幅相等、频率相同的特点。

在一些物理问题中，我们需要对多个同方向、同频率的简谐振动进行合成，以求得其合成振动后的运动规律。

而三角函数法是一种常用的数学方法，可以用来对这种问题进行求解。

本文将介绍三角函数法对同方向同频率简谐振动合成的求解过程，并给出具体的计算方法。

我们来看看什么是同方向同频率的简谐振动。

同方向是指振动的方向相同，即物体在振动过程中只沿着一个方向上做来回运动；同频率是指振动的频率相同，即两个或多个振动的周期都相同。

假设有两个同向同频率的简谐振动分别为x_1(t)=A_1\cos(\omegat+\varphi_1)和x_2(t)=A_2\cos(\omega t+\varphi_2)，其中A_1和A_2分别为振幅，\omega为角频率，\varphi_1和\varphi_2为初始相位。

要求解这两个简谐振动的合成振动，可以使用三角函数法。

三角函数法的基本思想是将两个简谐振动用三角函数表达式表示，然后将它们相加，再利用三角函数的和差化积公式将其合并为一个三角函数，最后根据初相位和振幅的关系求得合成振动的表达式。

下面我们以具体的例子来说明三角函数法对同方向同频率简谐振动合成的求解过程。

假设有两个同向、同频率的简谐振动x_1(t)=3\cos(2t+\frac{\pi}{4})和x_2(t)=4\cos(2t+\frac{\pi}{3})，现在要求解它们的合成振动。

接下来，利用三角函数的和差化积公式将上式合并为一个三角函数。

根据公式\cos\alpha+\cos\beta=2\cos\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}，我们有：x(t)=2\cos(2t+\frac{5\pi}{12})\cos(\frac{\pi}{12})+2\sin(2t+\frac{\pi}{12})\si n(\frac{\pi}{12})根据初相位和振幅的关系，我们可以得到合成振动的最终表达式为x(t)=2\sqrt{7}\cos(2t+\frac{5\pi}{12}+\theta)，其中\theta=\arctan(\frac{1}{\sqrt{7}})。