四杆桁架计算设置
- 格式:ppt
- 大小:61.00 KB
- 文档页数:17
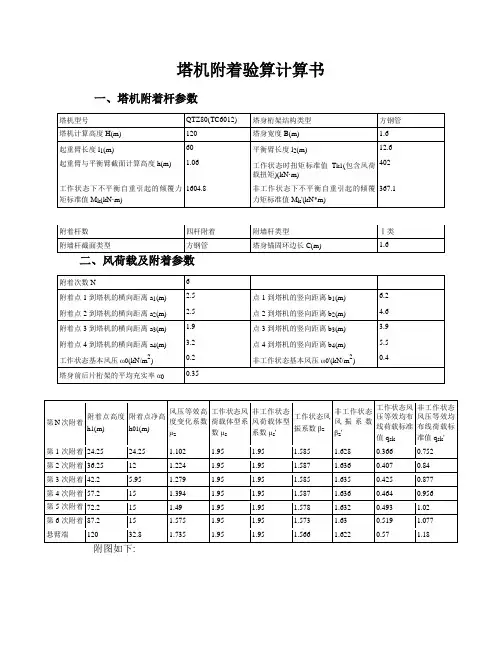
塔机附着验算计算书一、塔机附着杆参数二、风荷载及附着参数塔机附着立面图三、工作状态下附墙杆内力计算1、扭矩组合标准值T k回转惯性力及风荷载产出的扭矩标准值:T k=T k1=402kN·m2、附着支座反力计算计算简图剪力图得:R E=195.919kN在工作状态下,塔机起重臂位置的不确定性以及风向的随机性,在计算支座7处锚固环截面内力时需考虑塔身承受双向的风荷载和倾覆力矩及扭矩。
3、附墙杆内力计算支座7处锚固环的截面扭矩T k(考虑塔机产生的扭矩由支座7处的附墙杆承担),水平内力N w=20.5R E=277.071kN。
计算简图:塔机附着示意图塔机附着平面图α1=arctan(b1/a1)=68.039°α2=arctan(b2/a2)=61.477°α3=arctan(b3/a3)=64.026°α4=arctan(b4/a4)=59.808°β1=arctan((b1-c/2)/(a1+c/2))=58.57°β2=arctan((b2+c/2)/(a2+c/2))=58.57°β3=arctan((b3+c/2)/(a3+c/2))=60.124°β4=arctan((b4-c/2)/(a4+c/2))=49.6°四杆附着属于一次超静定结构,用力法计算,切断T4杆并代以相应多余未知力X1=1。
δ11× X1+Δ1p=0X1=1时,各杆件轴力计算:T11×sin(α1-β1)×(b1-c/2)/sinβ1+T21×sin(α2-β2)×(b2+c/2)/sinβ2-T31×sin(α3-β3)×(b3+c/2)/sinβ-1×sin(α4-β4)×(b4-c/2)/sinβ4=03T11×cosα1×c-T31×sinα3×c-1×cosα4×c-1×sinα4×c=0T21×cosα2×c+T31×sinα3×c-T31×cosα3×c+1×sinα4×c=0当N w、T k同时存在时,θ由0~360°循环,各杆件轴力计算:T1p×sin(α1-β1)×(b1-c/2)/sinβ1+T2p×sin(α2-β2)×(b2+c/2)/sinβ2-T3p×sin(α3-β3)×(b3+c/2)/sinβ-T k=03T1p×cosα1×c-T3p×sinα3×c-N w×sinθ×c/2+N w×cosθ×c/2-T k=0T2p×cosα2×c-T3p×sinα3×c+T3p×cosα3×c-N w×sinθ×c/2-N w×cosθ×c/2-T k=0δ11=Σ(T12L/(EA))=T112(a1/cosα1)/(EA)+T212(a2/cosα2)/(EA)+T312(a3/cosα3)/(EA)+12(a4/co sα4)/(EA)Δ1p=Σ(T1×T p L/(EA))=T11×T1p(a1/cosα1)/(EA)+T21×T2p(a2/cosα2)/(EA)+T31×T3p(a3/cosα3) /(EA)X1= -Δ1p/δ11各杆轴力计算公式如下:T1= T11×X1+ T1p,T2= T21×X1+T2p,T3=T31×X1+T3p,T4=X1(1)θ由0~360°循环,当T k按图上方向设置时求解各杆最大轴拉力和轴压力:最大轴压力T1=494.945kN,T2=209.245kN,T3=594.77kN,T4=0kN最大轴拉力T1=0kN,T2=781kN,T3=141.923kN,T4=364.272kN(2)θ由0~360°循环,当T k按图上反方向设置时求解各杆最大轴拉力和轴压力:最大轴压力T1=0kN,T2=781kN,T3=141.924kN,T4=364.272kN最大轴拉力T1=494.945kN,T2=209.246kN,T3=594.769kN,T4=0kN四、非工作状态下附墙杆内力计算此工况下塔机回转机构的制动器完全松开,起重臂能随风转动,故不计风荷载产生的扭转力矩。

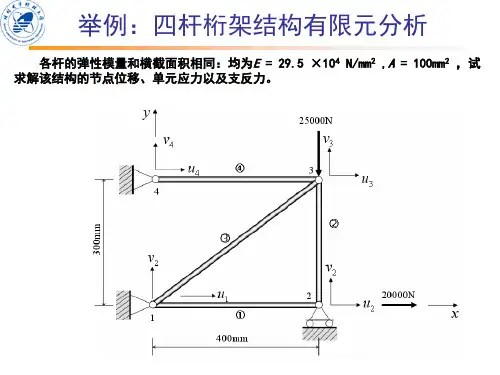
四杆桁架结构的有限元分析下面针对【典型例题】(1)的问题,在ANSYS 平台上,完成相应的力学分析。
即如图3-8所示的结构,各杆的弹性模量和横截面积都为4229.510N/mm E,E=29.5X10 2100mm A ,基于ANSYS 平台,求解该结构的节点位移、单元应力以及支反力。
图3-8 四杆桁架结构解答 对该问题进行有限元分析的过程如下。
以下为基于ANSYS 图形界面( graphic user interface ,GUI)的菜单操作流程;注意:符号“→”表示针对菜单中选项的鼠标点击操作。
关于ANSYS 的操作方式见附录B 。
1. 基于图形界面的交互式操作(step by step)(1) 进入ANSYS(设定工作目录和工作文件)程序 →ANSYS → ANSYS Interactive →Working directory (设置工作目录) →Initial jobname (设置工作文件名): planetruss →Run → OK(2) 设置计算类型ANSYS Main Menu : Preferences… → Structural → OK(3) 选择单元类型ANSYS Main Menu : Preprocessor →Element Type →Add/Edit/Delete… →Add… →Link :2D spar 1 →OK (返回到Element Types 窗口) →Close(4) 定义材料参数ANSYS Main Menu : Preprocessor →Material Props →Material Models →Structural →Linear →Elastic → Isotropic: EX:2.95e11 (弹性模量),PRXY: 0 (泊松比) → OK → 鼠标点击该窗口右上角的“ ”来关闭该窗口(5) 定义实常数以确定单元的截面积ANSYS Main Menu: Preprocessor →Real Constant s… →Add/Edit/Delete →Add →Type 1→ OK →Real Constant Set No: 1 (第1号实常数), AREA: 1e-4 (单元的截面积) →OK →Close(6) 生成单元 ANSYS Main Menu: Preprocessor →Modeling →Creat →Nodes → In Active CS →Node number 1 → X:0,Y:0,Z:0 →Apply →Node number 2 → X:0.4,Y:0,Z:0 →Apply →Node number 3 → X:0.4,Y:0.3,Z:0→Apply →Node number 4 → X:0,Y:0.3,Z:0→OKANSYS Main Menu: Preprocessor → Modeling → Create → Elements →Elem Attributes (接受默认值)→Usernumbered→Thru nodes→OK→选择节点1,2→Apply→选择节点2,3→Apply→选择节点1,3→Apply→选择节点3,4→Apply→OK(7)模型施加约束和外载添加位移的约束,分别将节点1 X和Y方向、节点2 Y方向、节点4的X和Y方向位移约束。


2D四杆桁架结构的有限元分析实例2D四杆桁架结构是一种常见的结构形式,广泛应用于工程领域。
在进行结构设计和分析时,有限元分析是一种常用的方法,可以对结构进行力学性能和应力分布的分析。
下面将以一个具体的例子来介绍2D四杆桁架结构的有限元分析。
```A*/\/\/\*-------*BC```该桁架结构由四根杆件构成,材料为钢,杆件截面可视为圆形。
假设桁架结构的高度为H,宽度为W,杆件的直径为D,且杆件AB和BC的长度为L。
首先,我们需要将该桁架结构离散为有限元网格。
可以采用等距离离散方法,在杆件AB上取N个节点,在杆件BC上取M个节点。
每个节点的坐标可以通过计算得到。
接下来,我们需要确定边界条件。
假设桁架结构的支座在节点A和C 处。
我们可以将节点A和C固定,即其位移为零,这是考虑到节点A和C作为支座点不会产生水平和竖直的位移。
然后,我们需要为杆件的材料属性和截面属性建立数学模型。
假设桁架结构的钢材的弹性模量为E,泊松比为ν。
另外,我们需要确定杆件的截面半径r。
接下来,我们需要确定桁架结构的荷载。
假设在节点B作用一个竖直向下的荷载P。
这个荷载会使得杆件AB和杆件BC受到拉力。
然后,我们可以使用有限元软件进行计算。
在计算中,我们可以采用线性弹性模型进行计算,即假设所有杆件在加载之前是弹性的。
在计算中,我们可以使用有限元方法对每个单元进行力学性能和应力分布的分析。
可以使用线性弹性有限元方法,如直接刚度法或变分法等。
在计算得到每个单元的力学性能和应力分布后,我们可以进一步分析整个桁架结构的强度和刚度。
可以计算整个结构的位移、载荷和应力等。
最后,我们可以通过对结果进行后处理和分析,来评估桁架结构的性能和稳定性。
可以计算结构的应力、变形和应变等。
综上所述,2D四杆桁架结构的有限元分析可以通过离散桁架结构为有限元网格,确定边界条件、材料和截面属性,施加荷载,并使用有限元软件进行计算。
通过对每个单元的力学性能和应力分布进行分析,并综合整个结构的性能和稳定性,可以得到结构的位移、载荷和应力等信息。
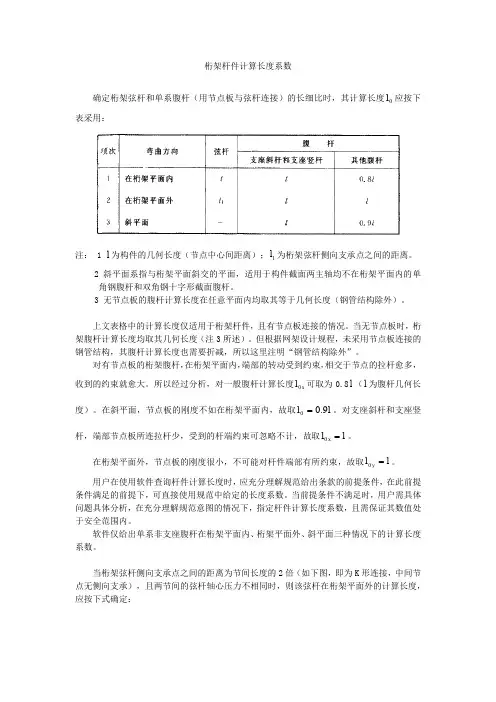
桁架杆件计算长度系数确定桁架弦杆和单系腹杆(用节点板与弦杆连接)的长细比时,其计算长度0l 应按下表采用:注: 1 l 为构件的几何长度(节点中心间距离);1l 为桁架弦杆侧向支承点之间的距离。
2 斜平面系指与桁架平面斜交的平面,适用于构件截面两主轴均不在桁架平面内的单角钢腹杆和双角钢十字形截面腹杆。
3 无节点板的腹杆计算长度在任意平面内均取其等于几何长度(钢管结构除外)。
上文表格中的计算长度仅适用于桁架杆件,且有节点板连接的情况。
当无节点板时,桁架腹杆计算长度均取其几何长度(注3所述)。
但根据网架设计规程,未采用节点板连接的钢管结构,其腹杆计算长度也需要折减,所以这里注明“钢管结构除外”。
对有节点板的桁架腹杆,在桁架平面内,端部的转动受到约束,相交于节点的拉杆愈多,收到的约束就愈大。
所以经过分析,对一般腹杆计算长度x l 0可取为0.8l (l 为腹杆几何长度)。
在斜平面,节点板的刚度不如在桁架平面内,故取l l 9.00=。
对支座斜杆和支座竖杆,端部节点板所连拉杆少,受到的杆端约束可忽略不计,故取l l x =0。
在桁架平面外,节点板的刚度很小,不可能对杆件端部有所约束,故取l l y =0。
用户在使用软件查询杆件计算长度时,应充分理解规范给出条款的前提条件,在此前提条件满足的前提下,可直接使用规范中给定的长度系数。
当前提条件不满足时,用户需具体问题具体分析,在充分理解规范意图的情况下,指定杆件计算长度系数,且需保证其数值处于安全范围内。
软件仅给出单系非支座腹杆在桁架平面内、桁架平面外、斜平面三种情况下的计算长度系数。
当桁架弦杆侧向支承点之间的距离为节间长度的2倍(如下图,即为K 形连接,中间节点无侧向支承),且两节间的弦杆轴心压力不相同时,则该弦杆在桁架平面外的计算长度,应按下式确定:⎪⎪⎭⎫ ⎝⎛+=121025.075.0N N l l 参数说明: 0l 为K 形节点时,弦杆侧向支承点之间的距离为节间长度的2倍,中间节点无侧向支承的情况下,桁架弦杆的平面外计算长度;1l 为桁架弦杆侧向支承点之间的距离(见上图),即节间长度l 的2倍(约等于);1N 为较大压力(两段弦杆中压力较大段的压力值),计算时取正值;2N 为较小压力或拉力(两段弦杆中压力较小段的压力值,或受拉的弦杆拉力值),计算时压力取正值,拉力取负值。

renchunmin一、设计计算资料1. 办公室平面尺寸为18m ×66m ,柱距8m ,跨度为32m ,柱网采用封闭结合。
火灾危险性:戊类,火灾等级:二级,设计使用年限:50年。
2. 屋面采用长尺复合屋面板,板厚50mm ,檩距不大于1800mm 。
檩条采用冷弯薄壁卷边槽钢C200×70×20×2.5,屋面坡度i =l/20~l/8。
3. 钢屋架简支在钢筋混凝土柱顶上,柱顶标高9.800m ,柱上端设有钢筋混凝土连系梁。
上柱截面为600mm ×600mm ,所用混凝土强度等级为C30,轴心抗压强度设计值f c =14.3N/mm 2。
抗风柱的柱距为6m ,上端与屋架上弦用板铰连接。
4. 钢材用 Q235-B ,焊条用 E43系列型。
5. 屋架采用平坡梯形屋架,无天窗,外形尺寸如下图所示。
6. 该办公楼建于苏州大生公司所属区内。
7. 屋盖荷载标准值:(l) 屋面活荷载 0.50 kN/m 2(2) 基本雪压 s 0 0.40 kN/m 2(3) 基本风压 w 0 0.45 kN/m 2(4) 复合屋面板自重 0.15 kN/m 2(5) 檩条自重 查型钢表(6) 屋架及支撑自重 0.12+0. 01l kN/m 28. 运输单元最大尺寸长度为9m ,高度为0.55m 。
二、屋架几何尺寸的确定1.屋架杆件几何长度屋架的计算跨度mm L l 17700300180003000=-=-=,端部高度取mmH 15000=跨中高度为mm 1943H ,5.194220217700150020==⨯+=+=取mm L i H H 。
跨中起拱高度为60mm (L/500)。
梯形钢屋架形式和几何尺寸如图1所示。
120图1 梯形屋架形式和几何尺寸(虚线为起拱后轮廓)2.檩条、拉条、及撑杆:长尺复合屋面板可以不考虑搭接需要,檩条最大允许间距为1800mm 。
另外,屋架上弦节点处一般应设檩条。

罐笼桁架设计计算说明书一、桁架结构图1. 桁架结构特点及主要尺寸桁架为空间桁架结构,由四根圆钢管(外径:Φ75mm ,壁厚7.5mm )做为主肢,加等边角钢的斜腹杆和横腹杆组焊而成。
主肢外包尺寸0.65×0.65m ×15m ,根据<<钢结构设计规范>>标准节每节高3 m.标准节,材料均为Q345。
抗拉、抗压强度为295,抗剪强度为170,断面承压fce=400 Mpa 。
.整个桁架连接在整块的钻井平台固定支座上。
桁架结构简化模型,主要尺寸见下图。
钻井平台罐笼钢丝绳罐道制动绳标准架绞车滑轮主绳桁架各部件重量见表一。
表一:主要性能参数表2. 计算工况及方位的确定2.1计算工况计算按独立式静止工况进行计算。
额定重量见上表,高15m。
3、桁架几何特性3.1 标准节几何特性3.1.1 标准节主肢主肢材料:圆钢管:D=75mm,d=67.5mm截面积:惯性矩:4、单肢强度校核:一、压杆所受的工作压力:F1=12.5KN二、强度校核:【σ】许用压强度:295Mpa三、稳定性校核:1、回转半径:2、柔度系数:其中:μ是长度因数,根据稳定理论取μ=1单肢计算长度:l=15000mm[λ]是柔度:钢材的柔度大于100是大柔度杆。
3、确定临界力:4、稳定条件:【n】是稳定系数:根据《钢结构稳定理论与设计》钢材的稳定系数是:1.8~3.0。
故单肢稳定性不安全,需要加支撑。
5、整体校核1、整个截面面积:A=4A1=4×10683.75=4275mm22、整个截面惯性矩:整个界面因为是正方形所以x虚轴,y虚轴相等:I X=I Y=4I1=4×533859.5=2135438mm43、整体稳定验算:许用临界力:因为整体许用临界力小于荷载力,故整体也不稳定,需要加支撑。
5、钻井平台压应力计算:选取钢板时的压应力应当大于σ。


25您的位置:在线学习—>在线教程—>教学内容上一页返回目录下一页3.4 静定平面桁架教学要求掌握静定平面桁架结构的受力特点和结构特点,熟练掌握桁架结构的内力计算方法——结点法、截面法、联合法3.4.1 桁架的特点和组成3.4.1.1 静定平面桁架桁架结构是指若干直杆在两端铰接组成的静定结构。
这种结构形式在桥梁和房屋建筑中应用较为广泛,如南京长江大桥、钢木屋架等。
实际的桁架结构形式和各杆件之间的联结以及所用的材料是多种多样的,实际受力情况复杂,要对它们进行精确的分析是困难的。
但根据对桁架的实际工作情况和对桁架进行结构实验的结果表明,由于大多数的常用桁架是由比较细长的杆件所组成,而且承受的荷载大多数都是通过其它杆件传到结点上,这就使得桁架结点的刚性对杆件内力的影响可以大大的减小,接近于铰的作用,结构中所有的杆件在荷载作用下,主要承受轴向力,而弯矩和剪力很小,可以忽略不计。
因此,为了简化计算,在取桁架的计算简图时,作如下三个方面的假定:(1)桁架的结点都是光滑的铰结点。
(2)各杆的轴线都是直线并通过铰的中心。
(3)荷载和支座反力都作用在铰结点上。
通常把符合上述假定条件的桁架称为理想桁架。
3.4.1.2 桁架的受力特点桁架的杆件只在两端受力。
因此,桁架中的所有杆件均为二力杆。
在杆的截面上只有轴力。
3.4.1.3 桁架的分类(1)简单桁架:由基础或一个基本铰接三角形开始,逐次增加二元体所组成的几何不变体。
(图3-14a)(2)联合桁架:由几个简单桁架联合组成的几何不变的铰接体系。
(图3-14b)(3)复杂桁架:不属于前两类的桁架。
(图3-14c)3.4.2 桁架内力计算的方法桁架结构的内力计算方法主要为:结点法、截面法、联合法结点法――适用于计算简单桁架。
截面法――适用于计算联合桁架、简单桁架中少数杆件的计算。
联合法――在解决一些复杂的桁架时,单独应用结点法或截面法往往不能够求解结构的内力,这时需要将这两种方法进行联合应用,从而进行解题。
桁架力学计算公式Sheet3Sheet2Sheet1数值单位项目说明代号外伸梁,左端距支点A为M,右端距支点B为N,AB间距离为L 外伸梁左端伸出长Mmm支座间距离外伸梁右端伸出长LN支座反力RARB均布载荷集度q截面位置x以左端为基准最大弯矩MmaxmkN/mkNkN.m一、最大弯矩弦杆轴力N竖杆轴力斜杆轴力KN最大剪力Q桁架计算高度斜杆与竖杆的夹角β°单位为弧度,弧度=度/1803.1416 三、杆件强度计算上弦杆的毛截面积A1下弦杆的毛截面积A2竖杆的毛截面积斜杆的毛截面积A3A4选100×100×10角钢2根c㎡选100×100×10角钢2根选80×80×6角钢2根上弦杆回转半径ix1下弦杆回转半径cm竖杆回转半径斜杆回转半径ix3ix4上弦杆计算拉应力σc1上弦杆计算压应力σc2MPa许用压应力120MPa 许用拉应力120MPa 竖杆压应力σc3斜杆拉应力四、杆件稳定性计算二、杆件轴力计算参考手册P21-11参考手册P21-37参考手册P21-96弦杆的计算长度参考<>P169,lc=l(几何长度)竖杆、斜杆计算长度lc1lc2参考<>P169,lc=0.8l(几何长度)上弦杆长细比λ1下弦杆长细比λ2λp=120手册P21-97 斜杆长细比λ3竖杆长细比λ4λp=150手册P21-97 λp=200手册P21-97 上弦杆受压稳定性计算竖杆受压稳定性计算σ1σ2根据λ选取的稳定系数φ手册P21-97表21-5-6许用应力σp=120MPa许用应力σp=120MPa五、挠度计算h0桁架的毛截面惯性矩桁架的跨中截面对水平心轴的毛截面惯性矩IxVx2061000=E桁架竖向挠度cm4桁架力学计算表雪载0.3kN/㎡选75×75×8角钢2根弧度竖杆斜杆计算长度lc3参考第2版《钢结构》P420,近似计算公式参考2版<>P20,lc=l(几何长度)参考2版<>P20,lc=0.8l(几何长度)机栈桥外伸梁,左端距支点A为M,右端距支点B为N,AB间距离为L0.000.00.00.00.00.000.0000.00 .00 .00 .00 0.00 .00 .00 .00 00.00 .00 .00 0.00 00.00 -0.00 0.000.00 .00 0.00 .00.00.00.00.00-0.00 000.00 00.00 .00 0.00 000.00 00.00.00-0.00 000.00 00.00 .00 0.00 000.00 00.00 .00 000.00 000.00 000.00 .00 0.00 0.00.00 0.00 0.00 .00 0.00 0.00 .00 0.00 0.00 .00.00 0.00 000.00 00.00 .00.00-0.00 000.00 00.00.00 00000.00 .00.00.00.00 00.00.000.00.000.00.00 000.00 .00 0.00 00.00 0.00 .00 0.00 .00.00 0.00 .00.00.00.000.00 00.00 .00.00.00 00.00 .00.00.00 0.00 .00.00 00.00 0.00 -00.0000.00 0.00 .00 0.00 .00 0.00 .00 0.00 .00 -.00 000.00 00.00 .00.00 000.0000.00 .00-0.00 000.00 00.00 .00 0.00 000.00 00.00 .00 000.00 000.00 000.00 0.00 0.00.00 0.00 0.00 .00 0.00 0.00 .00 0.00 0.00 .00.00.00 000.00 00.00 .00.00-0.00 000.00 00.00.00 000000.00 .00.00.00.0000.00.00.00.000.00.00 000.00 .00 0.00 00.00 0.00 .00 0.00 .00。
25您的位置:在线学习—>在线教程—>教学内容上一页返回目录下一页3.4 静定平面桁架教学要求掌握静定平面桁架结构的受力特点和结构特点,熟练掌握桁架结构的内力计算方法——结点法、截面法、联合法3.4.1 桁架的特点和组成3.4.1.1 静定平面桁架桁架结构是指若干直杆在两端铰接组成的静定结构。
这种结构形式在桥梁和房屋建筑中应用较为广泛,如南京长江大桥、钢木屋架等。
实际的桁架结构形式和各杆件之间的联结以及所用的材料是多种多样的,实际受力情况复杂,要对它们进行精确的分析是困难的。
但根据对桁架的实际工作情况和对桁架进行结构实验的结果表明,由于大多数的常用桁架是由比较细长的杆件所组成,而且承受的荷载大多数都是通过其它杆件传到结点上,这就使得桁架结点的刚性对杆件内力的影响可以大大的减小,接近于铰的作用,结构中所有的杆件在荷载作用下,主要承受轴向力,而弯矩和剪力很小,可以忽略不计。
因此,为了简化计算,在取桁架的计算简图时,作如下三个方面的假定:(1)桁架的结点都是光滑的铰结点。
(2)各杆的轴线都是直线并通过铰的中心。
(3)荷载和支座反力都作用在铰结点上。
通常把符合上述假定条件的桁架称为理想桁架。
3.4.1.2 桁架的受力特点桁架的杆件只在两端受力。
因此,桁架中的所有杆件均为二力杆。
在杆的截面上只有轴力。
3.4.1.3 桁架的分类(1)简单桁架:由基础或一个基本铰接三角形开始,逐次增加二元体所组成的几何不变体。
(图3-14a)(2)联合桁架:由几个简单桁架联合组成的几何不变的铰接体系。
(图3-14b))3-14c复杂桁架:不属于前两类的桁架。
(图)3(.3.4.2 桁架内力计算的方法桁架结构的内力计算方法主要为:结点法、截面法、联合法结点法――适用于计算简单桁架。
截面法――适用于计算联合桁架、简单桁架中少数杆件的计算。
联合法――在解决一些复杂的桁架时,单独应用结点法或截面法往往不能够求解结构的内力,这时需要将这两种方法进行联合应用,从而进行解题。
桁架内力的计算3.4 静定平面桁架教学要求掌握静定平面桁架结构的受力特点和结构特点,熟练掌握桁架结构的内力计算方法——结点法、截面法、联合法3.4.1 桁架的特点和组成3.4.1.1 静定平面桁架桁架结构是指若干直杆在两端铰接组成的静定结构。
这种结构形式在桥梁和房屋建筑中应用较为广泛,如南京长江大桥、钢木屋架等。
实际的桁架结构形式和各杆件之间的联结以及所用的材料是多种多样的,实际受力情况复杂,要对它们进行精确的分析是困难的。
但根据对桁架的实际工作情况和对桁架进行结构实验的结果表明,由于大多数的常用桁架是由比较细长的杆件所组成,而且承受的荷载大多数都是通过其它杆件传到结点上,这就使得桁架结点的刚性对杆件内力的影响可以大大的减小,接近于铰的作用,结构中所有的杆件在荷载作用下,主要承受轴向力,而弯矩和剪力很小,可以忽略不计。
因此,为了简化计算,在取桁架的计算简图时,作如下三个方面的假定:(1)桁架的结点都是光滑的铰结点。
(2)各杆的轴线都是直线并通过铰的中心。
(3)荷载和支座反力都作用在铰结点上。
通常把符合上述假定条件的桁架称为理想桁架。
3.4.1.2 桁架的受力特点桁架的杆件只在两端受力。
因此,桁架中的所有杆件均为二力杆。
在杆的截面上只有轴力。
3.4.1.3 桁架的分类(1)简单桁架:由基础或一个基本铰接三角形开始,逐次增加二元体所组成的几何不变体。
(图3-14a)(2)联合桁架:由几个简单桁架联合组成的几何不变的铰接体系。
(图3-14b)(3)复杂桁架:不属于前两类的桁架。
(图3-14c)3.4.2 桁架内力计算的方法桁架结构的内力计算方法主要为:结点法、截面法、联合法结点法――适用于计算简单桁架。
截面法――适用于计算联合桁架、简单桁架中少数杆件的计算。
联合法――在解决一些复杂的桁架时,单独应用结点法或截面法往往不能够求解结构的内力,这时需要将这两种方法进行联合应用,从而进行解题。
解题的关键是从几何构造分析着手,利用结点单杆、截面单杆的特点,使问题可解。