
第二十六章 二次函数
一、知识点盘点
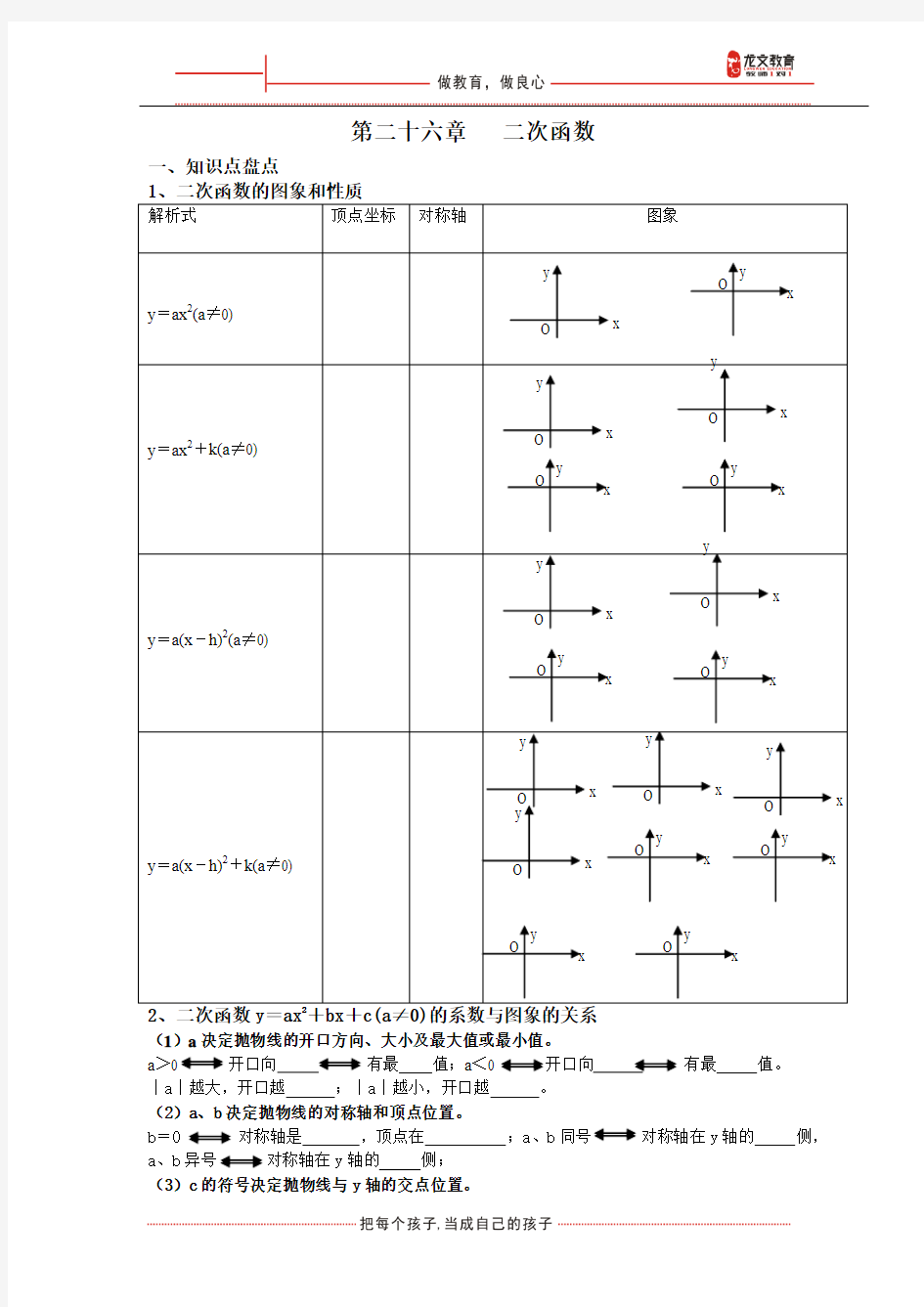
1、二次函数的图象和性质
解析式 顶点坐标 对称轴 图象
y =ax 2(a ≠0)
y =ax 2+k(a ≠0)
y =a(x -h)2(a ≠0)
y =a(x -h)2+k(a ≠0)
2、二次函数y =ax 2+bx +c(a ≠0)的系数与图象的关系
(1)a 决定抛物线的开口方向、大小及最大值或最小值。
a >0 开口向 有最 值;a <0 开口向 有最 值。 ︱a ︱越大,开口越 ;︱a ︱越小,开口越 。 (2)a 、
b 决定抛物线的对称轴和顶点位置。
b =0 对称轴是 ,顶点在 ;a 、b 同号 对称轴在y 轴的 侧, a 、b 异号 对称轴在y 轴的 侧; (3)
c 的符号决定抛物线与y 轴的交点位置。
x
y O
x
y
O
x
y O x
y
O x y
O x y
O
x
y O x
y O x
y O x y
O x y
O
x
y O x
y O x
y
O
x y
O x y
O x
y O
x
y
O
(0,c )是抛物线与y 轴的交点坐标。当c =0 抛物线过 ;c >0 抛物线交y 轴 ;c <0 抛物线交y 轴 。 (4)b 2-4ac 的符号决定抛物线与x 轴公共点的个数
b 2-4a
c >0 抛物线与x 轴有 个公共点;b 2-4ac =0 抛物线与x 轴有 个公共点;b 2-4ac <0 抛物线与x 轴有 个公共点。 (5)抛物线的特殊位置与系数的关系
顶点在x 轴上 b 2-4ac 0;顶点在y 轴上 b 0;
顶点在原点 ;抛物线经过原点 。 3、二次函数关系式的形式及对称轴、顶点坐标
(1)一般式:y =ax 2+bx +c(a ≠0),其对称轴为直线x =- b
2a
,顶点坐标 为(- b
2a ,4ac -b 2
4a
).
(2)顶点式:y =a(x -h)2+k(a ≠0),其对称轴为直线x =h ,顶点坐标为(h,k )。
(3)交点式:y =a(x -x 1)(x -x 2) (a ≠0 ),其中x 1,x 2是抛物线与x 轴两个交点的横坐标,即一元二次方程ax 2+bx +c =0(a ≠0)的两个根。 4、抛物线的平移规律
将抛物线y =ax 2(a ≠0)沿y 轴向上( )或向下( )平移︱k ︱个单位长度,即可得到抛物线y =ax 2+k(a ≠0);将抛物线y =ax 2(a ≠0)沿x 轴向左( )或向右( )平移︱h ︱个单位长度,即可得到抛物线y =a(x -h)2(a ≠0);将抛物线
y =ax 2(a ≠0)沿x 轴向左( )或向右( )平移︱h ︱个单位长度,即可得到抛物线 ,然后再将得到的抛物线沿y 轴向上( )或向下 ( )平移︱k ︱个单位长度,即可得到抛物线y =a(x -h)2+k(a ≠0)。 5、二次函数最值的求法
(1)配方法:将抛物线y =ax 2+bx +c(a ≠0)用配方法化为y =a(x -h)2+k(a ≠0)的形式,顶点坐标为(h,k ),对称轴为直线x =h,当a >0时,y 有最小值,即当x =h 时,y 最小值=k ;当a <0时,y 有最大值,即当x =h 时,y 最大值=k 。
(2)公式法:直接利用顶点坐标公式。
当a >0时,y 有最 值,即当x =- b
2a 时,y 最小值=4ac -b 2
4a ;当a <0时,y 有最 值,即当x =-
b
2a 时,y 最大值=4ac -b 2
4a
。 6、二次函数y =ax 2+bx +c(a ≠0)与一元二次方程ax 2+bx +c =0(a ≠0)的关系
二次函数y =ax 2+bx +c(a ≠0)与x 轴有两个公共点(x 1,0)、(x 2,0) 一元二次方程ax 2+bx +c =0(a ≠0)有两个不相等的实数根x =x 1,x =x 2 b 2-4ac >0;
二次函数y =ax 2+bx +c(a ≠0)与x 轴有唯一公共点(x 1,0) 一元二次方程ax 2+bx +c =0(a ≠0)有两个相等的实数根x =x 1=x 2 b 2-4ac =0;
二次函数y =ax 2+bx +c(a ≠0)与x 轴没有公共点 一元二次方程ax 2+bx +c =0(a ≠0)没有实数根 b 2-4ac <0。 二、知识点达标练习
1、下列函数中,是二次函数关系的是( )
A 、y =x +1x
B 、y =x 3
x C 、y =(3x -1)2-9x 2 D 、y =(x +2)2-4x
2、已知四个函数(1)y =-4x ;(2)y =12 x -3;(3)y =10
x
(x <0);(4)y =-x 2(x >0)。
其中y 随着x 的增大而减小的函数有: (填序号)
3、在自由落体运动中,物体下落的高度h 关于时间t 的函数关系为h =1
2 gt 2,其中g 为重力加速度(是
一个常数),那么这个函数的图象是( )
A B 、 C D
4、在同一坐标系中,一次函数y =ax +c 和二次函数y =ax 2+c 的图象大致是( )
A B C D
5、将抛物线y =-x 2+1先向上平移3个单位长度,然后再向右平移5个单位长度,所得到的抛物线的解析式是: ;
6、请你写出一个顶点坐标为(-2,2)的抛物线解析式: ;
7、抛物线y =-(x -3)2
+4与x 轴的交点坐标是 ,与y 轴的交点坐标为 ; 8、若抛物线(x -a)2+a +1的顶点在第二象限,则a 的取值范围是: ;
9、二次函数y =ax 2+bx +c(a ≠0)的图象如图所示,则下列关于a 、b 、c 间的关系正确的是( ) A 、ab <0 B 、bc <0 C 、a +b +c >0 D 、a -b +c <0 10、如图所示的抛物线是二次函数y =ax 2-3x +a 2
-1的图象, 那么a 的值是 ;
11、如图所示的是二次函数y =ax 2+bx +c(a ≠0)的图象的一部分,
根据图象提供的信息,下列结论中正确的有 (填序号)
(1)b >0;(2)c >0;(3)b 2-4ac <0;
(4)a +b +c <0;(5)2a >b. 12、二次函数y =a(x -1)2+c 的图象如图 所示,则直线y =―ax ―c 不经过第 象限。 13、已知抛物线y =x 2
-2x -2的顶点为A,与y 轴交于点B , 求过A 、B 两点的直线的解析式。
14、已知二次函数y =-x 2+2x +m 的部分图象如图所示, 则关于x 的一元二次方程-x 2
+2x +m =0的解为 。 15、已知一抛物线与x 轴的交点是A (-2,0),B (1,0),且经过 点C (2,8)。
t h O t h O t h O t
h O
x y O x y O x y O x y O
y
x O 第9题图 O x
y
第10题图
O
x y · -1 第11题图 O x
y
1
第12题图 O x
y 1 3 第14题图
(1)求该抛物线的解析式;
(2)求该抛物线的顶点坐标。
16、将下列函数化成y=a(x-h)2+k(a≠0)的形式,并分别指出抛物线的开口方向、顶点坐标、和对称轴。
(1)y=-2x2+5x-3 (2)y=1
2x
2-2x+1
17、已知一条抛物线的顶点坐标为(-1,2),且这条抛物线经过点A(1,-2)。求这条抛物线
的函数关系式。
18、一条抛物线与x轴交点的横坐标分别为-3,1,与y轴交点的纵坐标为-2。求这条抛物线的
解析式。
19、有研究发现,人体在注射一定剂量的某种药物后的数小时内,体内血液中的药物浓度(即血药浓度)y(毫克/升)是时间t(小时)的二次函数,已知某病人的三次化验结果如下表:t(小时)0 1 2
Y(毫克/升)0 0.14 0.24
(1)求y与t之间的函数关系式;
(2)在注射后的第几小时,该病人体内的血药浓度达到最大?最大浓度是多少?
(3)该病人在注射后的几个小时内,体内的血药浓度超过0.3毫克/升?
提高题:二次函数y=x2+bx+c的图象向左平移2个单位长度,再向上平移3个单位长度,得二次函数y=x2-2x+1的图象,求b和c。
二次函数知识点总结 二次函数知识点: 1.二次函数的概念:一般地,形如2y ax bx c =++(a b c , ,是常数,0a ≠)的函数,叫做二次函数。 这里需要强调:和一元二次方程类似,二次项 系数0a ≠,而b c , 可以为零.二次函数的定义域是全体实数. 2. 二次函数2y ax bx c =++的结构特征: ⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2. ⑵ a b c , ,是常数,a 是二次项系数,b 是一次项系数,c 是常数项. 二次函数的基本形式 1. 二次函数基本形式:2y ax =的性质: 结论:a 的绝对值越大,抛物线的开口越小。 总结:
2. 2 =+的性质: y ax c 结论:上加下减。 总结:
3. ()2 =-的性质: y a x h 结论:左加右减。 总结: 4. ()2 =-+的性质: y a x h k
总结: 1. 平移步骤: ⑴ 将抛物线解析式转化成顶点式()2 y a x h k =-+,确定其顶点坐标()h k ,; ⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法 如下:
【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位 2. 平移规律 在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”. 概括成八个字“左加右减,上加下减”. 三、二次函数()2 y a x h k =-+与2y ax bx c =++的比较 请将2245y x x =++利用配方的形式配成顶点式。请将2y ax bx c =++配成 ()2 y a x h k =-+。 总结: 从解析式上看,()2 y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者 通过配方可以得到前者,即2 2424b ac b y a x a a -? ?=++ ?? ?,其中2424b ac b h k a a -=-= ,. 四、二次函数2y ax bx c =++图象的画法 五点绘图法:利用配方法将二次函数2y ax bx c =++化为顶点式 2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧, 左右对称地描点画图.一般我们选取的五点为:顶点、与y 轴的交点()0c , 、以及()0c , 关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称的点). 画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点.
二次函数知识点归纳及提高训练 1.定义:一般地,如果c b a c bx ax y ,,(2 ++=是常数,)0≠a ,那么y 叫做x 的二次函数. 2.二次函数2 ax y =的性质 (1)抛物线2ax y =)(0≠a 的顶点是坐标原点,对称轴是y 轴.(2)函数2 ax y =的图像与a 的符号关系. ①当0>a 时?抛物线开口向上?顶点为其最低点;②当0a 时,开口向上;当0a b (即a 、b 同号)时,对称轴在y 轴左侧; ③0c ,与y 轴交于正半轴;③0 中考复习专题——二次函数知识点总结 一、二次函数的有关概念: 1、二次函数的定义: 一般地,形如2y ax bx c =++(a b c ,,是常数,0a ≠)的函数,叫做二次函数。 2、二次函数解析式的表示方法 (1) 一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠); (2) 顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠); (3) 两根式:12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标). 二、二次函数2y ax bx c =++图象的画法 1.基本方法:描点法 注:五点绘图法。利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一 般我们选取的五点为:顶点、与y 轴的交点()0c , 、以及()0c ,关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称 的点). 2.画草图 抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点. 三、二次函数的图像和性质 1.二次函数2y ax bx c =++的性质 (1). 当0a >时,抛物线开口向上,对称轴为2b x a =-,顶点坐标为2424b ac b a a ??-- ??? ,. 当2b x a <- 时,y 随x 的增大而减小;当2b x a >-时,y 随x 的增大而增大; 当2b x a =-时,y 有最小值244ac b a -. (2). 当0a <时,抛物线开口向下,对称轴为2b x a =-,顶点坐标为2424b ac b a a ??-- ??? ,. 当2b x a <- 时,y 随x 的增大而增大;当2b x a >-时,y 随x 的增大而减小; 当2b x a =-时,y 有最大值244ac b a -. 华东师大版数学九年级下册第26章二次函数单元测试题 一、选择题 1.将二次函数y=x2-2x+3化为y=(x-h)2+k的形式,结果为( ) A.y=(x+1)2+4 B.y=(x+1)2+2 C.y=(x-1)2+4 D.y=(x-1)2+2 2.把抛物线y=-x2向左平移1个单位,然后向上平移3个单位,则平移后的抛物线所对应的函数表达式为( ) A.y=-(x+1)2+3 B.y=-(x+1)2-3 C.y=-(x-1)2+3 D.y=-(x-1)2-3 2 x …-5 -4 -3 -2 -1 0 … y … 4 0 -2 -2 0 4 … A.抛物线的开口向下 B.当x>-3时,y随x的增大而增大 C.二次函数的最小值是-2 D.抛物线的对称轴是x=-5 2 4.若抛物线y=2x2+3上有三点A(1,y 1),B(5,y 2 ),C(-2,y 3 ),则y 1 ,y 2 ,y 3 的大小 关系为( ) A.y2<y1<y3 B.y2<y3<y1 C.y1<y3<y2 D.y3<y2<y1 5.如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( ) A.-1<x<5 B.x<-1且x>5 C.x<-1或x>5 D.x>5 6.将进货单价为70元的某种商品按零售价100元/个售出时每天能卖出20个,若这种商品的零售价在一定范围内每降价1元,其日销售量就增加1个,为了获得最大利润,则应降价( ) A.5元 B.10元 C.15元 D.20元 7.二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为( ) A.-3 B.3 C.-9 D.0 8.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-1,下列结 初三数学 二次函数 知识点总结 一、二次函数概念: 1.二次函数的概念:一般地,形如2y ax bx c =++(a b c ,,是常数, 0a ≠)的函数,叫做二次函数。 这里需要强调:和一元二次方程类似,二次项系数0a ≠,而b c ,可以为零.二次函数的定义域是全体实数. 2. 二次函数2y ax bx c =++的结构特征: ⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2. ⑵ a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项. 二、二次函数的基本形式 1. 二次函数基本形式:2y ax =的性质: a 的绝对值越大,抛物线的开口越小。 2. 2y ax c =+的性质: 上加下减。 3. ()2 y a x h =-的性质: 左加右减。 4. ()2 y a x h k =-+的性质: 三、二次函数图象的平移 1. 平移步骤: 方法一:⑴ 将抛物线解析式转化成顶点式()2 y a x h k =-+,确定其顶点坐标()h k ,; ⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下: 【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位 2. 平移规律 在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”. 概括成八个字“左加右减,上加下减”. 方法二: ⑴c bx ax y ++=2沿y 轴平移:向上(下)平移m 个单位,c bx ax y ++=2变成 m c bx ax y +++=2(或m c bx ax y -++=2) ⑵c bx ax y ++=2沿轴平移:向左(右)平移m 个单位,c bx ax y ++=2变成 c m x b m x a y ++++=)()(2(或c m x b m x a y +-+-=)()(2) 四、二次函数()2 y a x h k =-+与2y ax bx c =++的比较 从解析式上看,()2 y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者通过配方可以得到前者,即2 2424b ac b y a x a a -? ?=++ ?? ?,其中2424b ac b h k a a -=-= ,. 二次函数知识点整理: 1.二次函数的图象特征与a ,b ,c 及判别式ac b 42-的符号之间的关系 (1)字母a 决定抛物线的形状. 即开口方向和开口大小;决定二次函数有最大值或最小值. a >0时开口向上,函数有最小值; a <0时开口向下,函数有最大值; a 相同,抛物线形状相同,可通过平移、对称相互得到; a 越大,开口越小. (2)字母b 、a 的符号一起决定抛物线对称轴的位置. ab=0 (a ≠0,b=0), 对称轴为y 轴; ab >0(a 与b 同号),对称轴在y 轴左侧; ab <0(a 与b 异号),对称轴在y 轴右侧. (3)字母c 决定抛物线与y 轴交点的位置. c=0, 抛物线经过原点; c >0,抛物线与y 轴正半轴相交; c <0,抛物线与y 轴负半轴相交. (4)ac b 42-决定抛物线与x 轴交点的个数. ac b 42-=0,抛物线与x 轴有唯一交点(顶点); ac b 42->0抛物线与x 轴有两个不同的交点; ac b 42-<0抛物线与x 轴无交点. 2.任意抛物线()k h x a y +-=2 都可以由抛物线2ax y =经过平移得到,具体平移方法如 下: 【注意】 二次函数图象间的平移,可看作是顶点间的平移,因此只要掌握了顶点是如何平移的,就掌握了二次函数间的平移. 二次函数图象间对称变换也是同样的道理. 3.用待定系数法求二次函数的解析式 确定二次函数的解析式一般需要三个独立条件,根据不同条件选不同的设法 (1)设一般式:c bx ax y ++=2 (a ,b ,c 为常数、a ≠0) 若已知条件是图象上的三点,将已知条件代入所设一般式,求出a,b,c 的值 (2)设顶点式:()k h x a y +-=2 (a,h,k 为常数,a ≠0) 若已知二次函数图象的顶点坐标或对称轴方程与最大值(或最小值),将已知条件代入所设顶点式,求出待定系数,最后将解析式化为一般形式. (3)设两点式:()()21x x x x a y --=(a ≠0,a 、1x 、2x 为常数) 若已知二次函数图象与x 轴的两个交点的坐标为()()0,0,21x x ,将第三点(m,n ) 的坐标(其中m ,n 为已知数)或其他已知条件代入所设交点式,求出待定系数a ,最后将解析式化为一般形式. 4. 二次函数c bx ax y ++=2(a ≠0)与一元二次方程02=++c bx ax 的关系 (1)二次函数c bx ax y ++=2(a ≠0)中,当y=0时,就变成了一元二次方程02=++c bx ax (2)一元二次方程02=++c bx ax 的根就是二次函数c bx ax y ++=2的图象与x 轴交点的横坐标. (3)二次函数的图象与x 轴交点的个数与一元二次方程根的个数一致. (4)在它俩的关系中,判别式△=ac b 42-起着重要作用. 二次函数的图象与x 轴有两个交点?对应方程的△>0 二次函数的图象与x 轴有一个交点?对应方程的△=0 二次函数的图象与x 轴无交点 ?对应方程的△<0 5.二次函数应用 包括两方面 (1)用二次函数表示实际问题中变量之间的关系; (2)用二次函数解决最大化问题即最值问题. 新人教版九年级上二次函数知识点总结 知识点一:二次函数的定义 1.二次函数的定义: 一般地,形如(是常数,)的函数,叫做二次函数.2y ax bx c =++a b c ,,0a ≠其中是二次项系数,是一次项系数,是常数项. a b c 知识点二:二次函数的图象与性质抛物线的三要素:开口、对称轴、顶 ??点 2. 二次函数的图象与性质 ()2 y a x h k =-+(1)二次函数基本形式的图象与性质:a 的绝对值越大,抛物线的开口越小 2y ax = (2)的图象与性质:上加下减 2y ax c =+ (3)的图象与性质:左加右减 ()2 y a x h =- (4)二次函数的图象与性质 ()2 y a x h k =-+ 3. 二次函数的图像与性质 c bx ax y ++=2 (1)当时,抛物线开口向上,对称轴为,顶点坐标为. 0a >2b x a =-2424b ac b a a ??-- ??? ,当时,随的增大而减小;当时,随的增大而增大;当时,2b x a <- y x 2b x a >-y x 2b x a =-有最小值 .y 2 44ac b a - (2)当时,抛物线开口向下,对称轴为,顶点坐标为. 0a <2b x a =-2424b ac b a a ??-- ??? ,当时,随的增大而增大;当时,随的增大而减小;当时,2b x a <- y x 2b x a >-y x 2b x a =-有最大值 .y 2 44ac b a - 4. 二次函数常见方法指导 (1)二次函数2y ax bx c =++图象的画法①画精确图 五点绘图法(列表-描点-连线) 利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图. ②画草图 抓住以下几点:开口方向,对称轴,与y 轴的交点,顶点.(2)二次函数图象的平移平移步骤: ①将抛物线解析式转化成顶点式,确定其顶点坐标;()2 y a x h k =-+()h k ,② 可以由抛物线经过适当的平移得到具体平移方法如下: 2 ax 【【【(h <0)【【【 【【(h >0)【【【(h 【【|k|【【【 平移规律:概括成八个字“左加右减,上加下减”.(3)用待定系数法求二次函数的解析式①一般式:.已知图象上三点或三对、 的值,通常选择一般式. ②顶点式:.已知图象的顶点或对称轴,通常选择顶点式. ③交点式: .已知图象与轴的交点坐标 、 ,通常选择交点式. (4)求抛物线的顶点、对称轴的方法 ①公式法:,∴顶点是,对称轴a b ac a b x a c bx ax y 44222 2 -+ ??? ? ?+=++=),(a b ac a b 4422--是直线.a b x 2- =②配方法:运用配方的方法,将抛物线的解析式化为的形式,得到顶点为(, ()k h x a y +-=2 h ),对称轴是直线. k h x = 二次函数知识点归纳 一、二次函数概念 1.二次函数的概念:一般地,形如2y ax bx c =++(a b c ,,是常数,0a ≠)的函数,叫做二次函数。 这里需要强调:和一元二次方程类似,二次项系数0a ≠,而b c ,可以为零.二次函数的定义域是全体实数. 2. 二次函数2y ax bx c =++的结构特征: ⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2. ⑵ a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项. 二、二次函数的基本形式 1. 二次函数基本形式:2y ax =的性质: o o 结论:a 的绝对值越大,抛物线的开口越小。 总结: 2. 2y ax c =+的性质: 结论:上加下减。 a 的符号 开口方向 顶点坐标 对称轴 性质 0a > 向上 ()00, y 轴 0x >时,y 随x 的增大而增大;0x <时,y 随x 的增大而减小;0x =时,y 有最小值0. 0a < 向下 ()00, y 轴 0x >时,y 随x 的增大而减小;0x <时,y 随x 的增大而增大;0x =时,y 有最大值0. 总结: 3. ()2 y a x h =-的性质: 结论:左加右减。 总结: 4. ()2 y a x h k =-+的性质: 总结: a 的符号 开口方向 顶点坐标 对称轴 性质 0a > 向上 ()0c , y 轴 0x >时,y 随x 的增大而增大;0x <时,y 随x 的增大而减小;0x =时,y 有最小值c . 0a < 向下 ()0c , y 轴 0x >时,y 随x 的增大而减小;0x <时,y 随x 的增大而增大;0x =时,y 有最大值c . a 的符号 开口方向 顶点坐标 对称轴 性质 0a > 向上 ()0h , X=h x h >时,y 随x 的增大而增大;x h <时,y 随x 的增大而减小;x h =时,y 有最小值0. 0a < 向下 ()0h , X=h x h >时,y 随x 的增大而减小;x h <时,y 随x 的增大而增大;x h =时,y 有最大值0. a 的符号 开口方向 顶点坐标 对称轴 性质 二次函数 一、解析式的求法 一般式2 y ax bx c =++?? ?已知没有规律的三个点的坐标 已知a:b:c,并且已知一个点的坐标 顶点式2 ()y a x m n =++????? 已知顶点及另一点的坐标已知对称轴和另外两点的坐标已知最值和另外两点的坐标 两点式(交点式)12()()y a x x x x =-- 二、二次函数的图像 1、二次函数的平移问题 (1)、平移的实质:a 相同。(a 决定二次函数的形状、开口和开口的大小,其中a 决定开口的大小,a 的正负决定开口方向。注意,两个二次函数的a 相等,则这两个二次函数的形状就是相同的) (2)、平移的规律:顶点坐标的平移。 2、二次函数的对称变换: 2222 ()(+)()(+)y a x m k y a x m k y y a x m k y a x m k x ?=-+=+?=-+=--?与关于轴对称 与关于轴对称 3、二次函数的图像与,,a b c 及其相关代数式(2 ,2,4a b c a b b ac ±+±-)之间的关系 0a a a ?>????L 对称轴在轴右侧对称轴在轴左侧0 00y y c c y y c ?>???? -?-=???- 二次函数知识点(第一讲) 一、二次函数概念: 1.二次函数的概念:一般地,形如2y ax bx c =++(a b c ,,是常数,0a ≠)的函数,叫做二次函数。 这里需要强调:和一元二次方程类似,二次项系数0a ≠,而b c ,可以为零.二次函数的定义域是全体实数. 2. 二次函数2y ax bx c =++的结构特征: ⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2. ⑵ a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项. 二、二次函数的基本形式 1. 二次函数基本形式:2y ax =的性质: a 的绝对值越大,抛物线的开口越小。 2. 2y ax c =+的性质:(上加下减) 3. ()2 y a x h =-的性质:(左加右减) 4. ()2 y a x h k =-+的性质: 三、二次函数图象的平移 1. 平移步骤: 方法一:⑴ 将抛物线解析式转化成顶点式()2 y a x h k =-+,确定其顶点坐标()h k ,; ⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k , 处,具体平移方法如下: 【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位 2. 平移规律 在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”.概括成八个字“左加右减,上加下减”. 方法二: ⑴c bx ax y ++=2沿y 轴平移:向上(下)平移m 个单位,c bx ax y ++=2变成 m c bx ax y +++=2(或m c bx ax y -++=2) ⑵c bx ax y ++=2沿轴平移:向左(右)平移m 个单位,c bx ax y ++=2变成 c m x b m x a y ++++=)()(2(或c m x b m x a y +-+-=)()(2) 四、二次函数() 2 y a x h k =-+与2 y ax bx c =++的比较 从解析式上看,()2 y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者通过配方可以得到 前者,即2 2424b ac b y a x a a -? ?=++ ??? ,其中2424b ac b h k a a -=-= ,. 五、二次函数2y ax bx c =++图象的画法 五点绘图法:利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方 向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为: 顶点、与y 轴的交点()0c , 、以及()0c ,关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称的点). 画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点. 六、二次函数2y ax bx c =++的性质 1. 当0a >时,抛物线开口向上,对称轴为2b x a =-,顶点坐标为2424b ac b a a ??-- ??? ,. 当2b x a <- 时,y 随x 的增大而减小;当2b x a >-时,y 随x 的增大而增大;当2b x a =-时,y 有最小值2 44ac b a -. 2. 当0a <时,抛物线开口向下,对称轴为2b x a =-,顶点坐标为2424b ac b a a ??-- ??? ,.当2b x a <- 时,y 随x 的增大而增大;当2b x a >-时,y 随x 的增大而减小;当2b x a =-时,y 有最大值244ac b a -. 七、二次函数解析式的表示方法 1. 一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠); 2. 顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠); 3. 两根式:12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标). 第26章 《二次函数》小结与复习(1) 教学目标: 理解二次函数的概念,掌握二次函数y =ax2的图象与性质;会用描点法画抛物线,能确定抛物线的顶点、对称轴、开口方向,能较熟练地由抛物线y =ax2经过适当平移得到y =a(x -h)2+k 的图象。 重点难点: 1.重点:用配方法求二次函数的顶点、对称轴,根据图象概括二次函数y =ax2图象的性质。 2.难点:二次函数图象的平移。 教学过程: 一、结合例题精析,强化练习,剖析知识点 1.二次函数的概念,二次函数y =ax 2 (a ≠0)的图象性质。 例:已知函数4m m 2x )2m (y -++=是关于x 的二次函数,求:(1)满足条件的m 值;(2)m 为何值时,抛物线有最低点?求出这个最低点.这时当x 为何值时,y 随x 的增大而增大?(3)m 为何值时,函数有最大值?最大值是什么?这时当x 为何值时,y 随x 的增大而减小? 学生活动:学生四人一组进行讨论,并回顾例题所涉及的知识点,让学生代表发言分析解题方法,以及涉及的知识点。 教师精析点评,二次函数的一般式为y =ax 2+bx +c(a ≠0)。强调a ≠0.而常数b 、c 可以为0,当b ,c 同时为0时,抛物线为y =ax 2(a ≠0)。此时,抛物线顶点为(0,0),对称轴是y 轴,即直线x =0。 (1)使4m m 2x )2m (y -++=是关于x 的二次函数,则m 2+m -4=2,且m +2≠0,即: m 2+m -4=2,m +2≠0,解得;m =2或m =-3,m ≠-2 (2)抛物线有最低点的条件是它开口向上,即m +2>0, (3)函数有最大值的条件是抛物线开口向下,即m +2<0。 抛物线的增减性要结合图象进行分析,要求学生画出草图,渗透数形结合思想,进行观察分析。 强化练习;已知函数m m 2x )1m (y ++=是二次函数,其图象开口方向向下,则m =_____,顶点为_____,当x_____0时,y 随x 的增大而增大,当x_____0时,y 随x 的增大而减小。 2。用配方法求抛物线的顶点,对称轴;抛物线的画法,平移规律,例:用配方法求出抛物线y =-3x 2-6x +8的顶点坐标、对称轴,并画出函数图象,说明通过怎样的平移,可得到抛物线y =-3x 2。 学生活动:小组讨论配方方法,确定抛物线画法的步骤,探索平移的规律。充分讨论后让学生代表归纳解题方法与思路。 教师归纳点评: (1)教师在学生合作讨论基础上强调配方的方法及配方的意义,指出抛物线的一般式与顶点 式的互化关系: y =ax 2+bx +c ————→y =a(x +b 2a )2+4ac -b 24a (2)强调利用抛物线的对称性进行画图,先确定抛物线的顶点、对称轴,利用对称性列表、描点、连线。 (3)抛物线的平移抓住关键点顶点的移动,分析完例题后归纳; 投影展示: 强化练习: (1)抛物线y =x 2+bx +c 的图象向左平移2个单位。再向上平移3个单位,得抛物线y =x 2-2x +1,求:b 与c 的值。最新中考复习二次函数知识点总结
华东师大数学九年级下《第26章二次函数》单元测试题含答案
初三数学二次函数知识点总结
二次函数知识点整理
(完整版)九年级上册数学二次函数知识点汇总,推荐文档
中考数学复习专题二次函数知识点归纳
初三数学二次函数练习题复习题二次函数知识点
(完整版)二次函数知识点汇总(全)
人教版数学九下《第26章二次函数》word小结与复习
二次函数知识点总结及典型题目