2013新人教版九下第26章《二次函数》word期末复习测试

2012-2013学年度第一学期期末考试九年级数学试题姓名___________ 命题人： (2013-1-12)一．选择题（每题3分，共30分）1．下列图形中，既是中心对称又是轴对称的图形是（ ☆ ）A B C D2．下列事件中，必然发生的为（ ☆ ）A. 我市冬季比秋季的平均气温低B. 走到车站公共汽车正好开过来C. 打开电视机正转播奥运会实况D. 掷一枚均匀硬币正面一定朝上3．在平面直角坐标系中，点P （2，－3）关于原点对称的点的坐标是（ ☆ ） A ．（2，3） B ．（－2，3） C ．（－2，－3） D ．（－3，2） 4．下列各式正确的是（ ☆ ） A.5323222=+=+ B. 32)53(3523++=+C. 94)9()4(⨯=-⨯-D. 212214=5．一元二次方程2x －2x ＋3＝0的根的情况是（ ☆ ）A.没有实数根B.有两个相等的实数根C.有两个不相等的实数根D.有两个实数根6．若⊙1O 的半径为cm 3，⊙2O 的半径为cm 4，且圆心距121cm O O =，则⊙1O 与⊙2O 的位置关系是（ ☆ ） A ．外离B ．内含C ．相交D ．内切7．把二次函数2114y x x =+-化为y =a (x +m )2+n 的形式是（ ☆ ）A ．21(1)24y x =++ B ．21(2)24y x =+- C ．21(2)24y x =-+ D ．21(2)24y x =--8．某种商品零售价经过两次降价后，每件的价格由原来的800元降为现在的578元，则平均每次降价的百分率为（ ☆ ） A ．10% B ．12% C ．15% D ．17%9．如图所示的向日葵图案是用等分圆周画出的，则⊙O 与半圆P 的半径的比为（ ☆ ） A.5﹕3 B.4﹕1 C.3﹕1 D.2﹕110．如图，若000a b c <><，，，则抛物线2y ax bx c =++的图象大致为（ ☆ ）二．填空题（每题3分，共18分，直接填写结果）11．若式子5+x 在实数范围内有意义，则x 的取值范围是 ．12．口袋内装有一些除颜色外完全相同的红球、白球和黑球，从中摸出一球，摸出红球的概率是0.2，摸出白球的概率是0.5，那么摸出黑球的概率是 ．13．已知P 是⊙O 外一点，PA 切⊙O 于A ，PB 切⊙O 于B.若PA ＝6，则PB ＝ ． 14．将抛物线21(5)33y x =--+向左平移5个单位，再向上平移3个单位后得到的抛物线的解析式为 ．15．已知抛物线2(0)y ax bx c a =++≠与x 轴的两个交点的坐标分别是（－3，0），（2，0），则方程20(0)ax bx c a ++=≠的解是____________________．16．如图，粮仓的顶部是圆锥形状，这个圆锥底面圆的半径长为3m ，母线长为6m ，为防止雨水，需在粮仓顶部铺上油毡，如果油毡的市场价是每平方米10元钱，那么购买油毡所需要的费用是 元（结果保留整数）． 三．解答题（本大题有4个小题，共34分）17．（8分）计算：)6332(2)23(2-+-18．（8分）解方程x （x -1）=2． 有学生给出如下解法：∵ x （x -1）=2=1×2=（-1）×（-2），∴ 1,12;x x =⎧⎨-=⎩或2,11;x x =⎧⎨-=⎩或1,12;x x =-⎧⎨-=-⎩或2,1 1.x x =-⎧⎨-=-⎩解上面第一、四方程组，无解；解第二、三方程组，得 x =2或x =-1．∴ x =2或x =-1．请问：这个解法对吗？试说明你的理由．如果你觉得这个解法不对，请你求出方程的解．19．（8分）如图，P为等边△ABC的中心．（1）画出将△ABP绕A逆时针旋转60°的图形；（不写画法，保留作图痕迹）（2）经过什么样的图形变换，可以把△ABP变换到右边的△CMN，请写出简要的文字说明．20．（10分）如图，⊙C经过原点且与两坐标轴分别交于点A和点B，点A的坐标为（0，2），D为⊙C在第一象限内的一点且∠ODB=60°，解答下列各题：（1）求线段AB的长及⊙C的半径；（2）求B点坐标及圆心C的坐标．四．解答题（学会用数学知识解决身边的实际问题！本大题有2个小题，共18分）21．（8分）宝宝和贝贝是一对双胞胎，他们参加迎新年长跑旗手选拔并与甲、乙、丙三人都进入了前5名．现从这5名入选者中确定2名作为旗手．试用画树形图或列表的方法求出：（1）宝宝和贝贝同时入选的概率；（2）宝宝和贝贝至少有一人入选的概率．22．（10分）在数学活动课上，同学们用一根长为1米的细绳围矩形．（1）小芳围出了一个面积为600㎝2的矩形，请你算一算，她围成的矩形的边长是多少？（2）小华想用这根细绳围成一个面积尽可能大的矩形，请你用所学过的知识帮他分析应该怎么围，并求出最大面积．五．解答题（学数学要善于观察思考，勇于探索！本大题有2个小题，共20分）23．（8分）先阅读，再回答问题：如果x1，x2是关于x的一元二次方程ax2＋bx＋c＝0(a≠0)的两个根，那么x1＋x2，x1x2与系数a，b，c的关系是：x1＋x2＝－ba，x1x2＝ca.例如：若x1，x2是方程2x2－x－1＝0的两个根，则x1＋x2＝－ba＝－－12＝12，x1x2＝ca＝－12＝－12．(1)若x1，x2是方程2x2＋x－3＝0的两个根，则x1＋x2＝，x1x2＝；(2)若x1，x2是方程x2＋x－3＝0的两个根，求x2x1＋x1x2的值．解：(1)x1＋x2＝，x1x2＝．(2)24．（12分）已知一条抛物线与y轴的交点为C，顶点为D，直线CD的解析式为3y x=+，并且线段CD的长为23．（1）求这条抛物线的解析式；（2）设（1）中的抛物线与x轴有两个交点A（1x，0）、B（2x，0），且点A在点B的左侧，求线段AB的长；（3）若以AB为直径作⊙M，请你判断直线CD与⊙M的位置关系，并说明理由．九年级数学试题答案和评分说明1~10：C A B C A D B C D B11． x ≥－5 12．0.3 13．6 14．6312+-=x y 15．1232x x =-=， 16．56517．原式=3+2-62+62-36=5－36．……8分18．解法不对……1分，理由略……4分，正确解法得到x =2或x =-1……8分．19．（1）图形略……3分；（2）先将△ABP 绕A 逆时针旋转60°，然后再将△ABP 绕B 顺时针旋转90°……6分；本题也可以先旋转，后平移，方法略．20．（1）连接AB ，∵∠ODB=∠OAB ，∠ODB=60°∴∠OAB=60°，∵∠AOB 是直角∴AB 是⊙C 的直径，∠OBA=30°，∴AB=2OA=4，∴⊙C 的半径r=2 ……5分 （2）在Rt △OAB 中，由勾股定理得：OB 2+ OA 2= AB 2， ∴OB=B 的坐标为：（0）……8分OF=BF=，过C 点作CE ⊥OA 于E ，CF ⊥OB 于F ，由垂径定理得： OE=AE=1，∴CE=CF=1，∴C1）……12分22．（1）设她围成的矩形的一边长为xcm ，得：60050=-）（x x ……2分， 302021==x x ，，当x =20时，3050=-x ㎝；当x =30时，cm x 2050=-，…4分所以小芳围成的矩形的两邻边分别是20㎝，30㎝……5分（2）设围成矩形的一边长为x c m ，面积为2ycm ，则有：50y x x =-（），即250y x x =-+，225625y x =--+（）……8分 当25x =时，y最大值=625；此时，2550=-x ，矩形成为正方形。

一、选择题1.(口答)下列函数中，哪些是二次函数?(1)y=5x ＋1 (2)y=4x2－1(3)y=2x3－3x2 (4)y=5x4－3x ＋12、二次函数c bx x y ++=2的图象上有两点(3，－8)和(－5，－8)，则此拋物线的对称轴是（ ）A ．x ＝4 B. x ＝3 C. x ＝－5 D. x ＝－1。

3、直角坐标平面上将二次函数y ＝-2(x －1)2－2的图象向左平移１个单位，再向上平移１个单位，则其顶点为（ ）A.(0，0) B.(1，－2) C.(0，－1) D.(－2，1)4、已知二次函数b x a y +-=2)1(有最小值 –1，则a 与b 之间的大小关系是 （ ）A ．a ＜bB ．a=bC ．a ＞bD ．不能确定二、填空题1、抛物线y=（k+1）x 2+k 2-9开口向下，且经过原点，则k ＝—————————2、已知抛物线y=x 2+（n-3）x+n+1经过坐标原点O ，求这条抛物线的顶点P 的坐标3、、二次函数c bx x y ++=2的图象上有两点(3，－8)和(－5，－8)，则此拋物线的对称轴是（ ）（A ）1x =- （B ）1x = （C ）2x =（D ）3x =4、顶点为（－2，－5）且过点（1，－14）的抛物线的解析式为___________________．5、已知二次函数y =ax 2+bx +c ，当x =1时，y 有最大值为5，且它的图象经过点（2，3），求这个函数的关系式.三、计算题1、某水果批发商场经销一种水果，如果每千克盈利10元，每天可售出500千克.经市场调查发现， 在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克.（10分）（1）当每千克涨价为多少元时，每天的盈利最多？最多是多少？（2）若商场只要求保证每天的盈利为6000元，同时又可使顾客得到实惠，每千克应涨价为多少元？2、如图（1），在Rt ⊿ABC 中，∠C=90°，BC=4，AC=8，点D 在斜边AB 上，分别作DE ⊥AC ，DF ⊥BC ，垂足分别为E 、F ，得四边形DECF ，设DE=x ，DF=y ．（1）用含y 的代数式表示AE ；（2）求y 与x 之间的函数关系式，并求出x 的取值范围；（3）设四边形DECF 的面积为S ，求S 与x 之间的函数关系，并求出S 的最大值．图（1） 图（2）参考答案选择题1.略 2、D 3、C 4、C填空题1．–3 2．（２，－４）３．Ａ４．ｙ＝－(ｘ＋２)2 －５５．ｙ＝－２ｘ２＋４ｘ＋３。

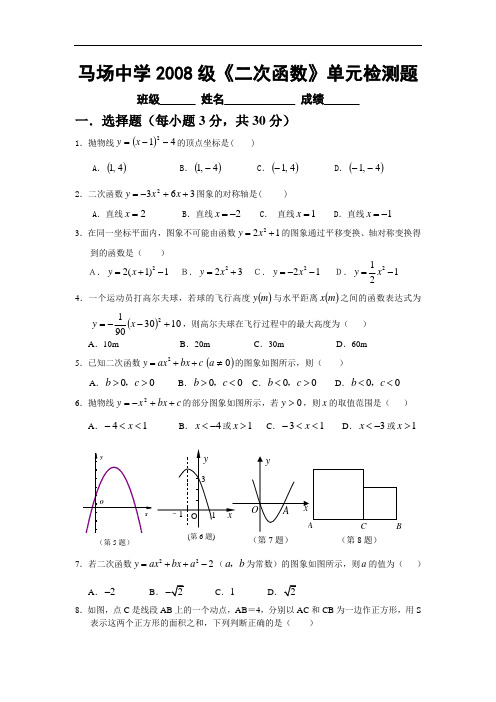
C B（第8题）马场中学2008级《二次函数》单元检测题班级＿＿＿ 姓名＿＿＿＿＿＿ 成绩＿＿＿一．选择题（每小题3分，共30分）1．抛物线()412--=x y 的顶点坐标是( )A ．()4,1B ．()4,1-C ．()4,1-D ．()4,1-- 2．二次函数3632++-=x x y 图象的对称轴是( )A ．直线2=xB ．直线2-=xC ． 直线1=xD ．直线1-=x 3．在同一坐标平面内，图象不可能由函数221y x =+的图象通过平移变换、轴对称变换得到的函数是（ ）Ａ．22(1)1y x =+- Ｂ．223y x =+ Ｃ．221y x =-- Ｄ．2112y x =- 4．一个运动员打高尔夫球，若球的飞行高度()m y 与水平距离()m x 之间的函数表达式为()10309012+--=x y ，则高尔夫球在飞行过程中的最大高度为（ ） A ．10m B ．20m C ．30m D ．60m 5．已知二次函数2y ax bx c =++()0≠a 的图象如图所示，则（ ）A ．00b c >>，B ．00b c ><，C ．00b c <>，D ．00b c <<，6．抛物线c bx x y ++-=2的部分图象如图所示，若0>y ，则x 的取值范围是（ ）A ．14<<-xB ．4-<x 或1>xC ．13<<-xD ．3-<x 或1>xa 的值为（ ） 和CB 为一边作正方形，用S（第13题） A ．当C 是AB 的中点时，S 最大 B ．当C 是AB 的中点时，S 最小 C ．当C 为AB 的三等分点时，S 最大 D ．当C 为AB 的三等分点时，S 最小 9、在同一直角坐标系中，一次函数y =ax +c 和二次函数y =ax 2+c 的图象大致为( )10、已知二次函数y =2x 2+8x +7的图象上有点A 1(2)y -，，B 21(5)3y -，C 31(1)5y -，，则 y 1、y 2、y 3的大小关系为( )A ． y 1 > y 2> y 3B ． y 2> y 1> y 3C ． y 2> y 3> y 1D ． y 3> y 2> y 1二．填空题（每小题3分，共24分）11．抛物线12-=x y 的开口向 ．12．当x ＝ 时，函数1)3(22--=x y 有最 值，这个值是 ． 13．当x 时，函数1)3(2-+-=x y 的y 随x 14．将抛物线22(1)3y x =+-向右平移1个单位，再向上平移3位后得到的抛物线的解析式为 ．15．已知二次函数22y x x m =-++的部分图象如图所示，则关于x的一元二次方程220x x m -++=的解为＿＿＿＿＿ ． 16．某商场将每件进价为80元的某种商品按每件100元出售，一天可售出100件．后来经过市场调查，发现这种商品单价每降低1元，其销量可增加10件．设后来该商品每件降价x 元，商场一天可获利润y 元．则y 与x 之间的函数关系式是＿＿＿＿＿＿． 17．二次函数2y ax bx c =++()0≠a 的部分对应值如下表：则二次函数2y ax bx c =++()0≠a 图象的对称轴为直线x = ． 18．如图是二次函数2y ax bx c =++()0≠a 图象的一部分，图象过点A （－3，0），对称轴为直线1-=x ．给出以下四个结论：①ac b 42>；②02=+b a ；③0=++c b a ；④b a <5．其中正确结论的的序号是＿＿＿＿＿．三．解答题（17、18每小题12分，19、20每小题11分，共46分）19．已知抛物线322++-=x x y ．（1）用配方法求它的顶点坐标和对称轴；（2）直接写出抛物线与x 轴的两个交点A 、B （点A 在点B 的左侧）及与y 轴的交点C的坐标； （3）在给出的坐标系中，画出函数322++-=x x y 的图象； （4）结合图象回答：当x 在什么范围时，y 随x 的增大而减小？2ax k y +=20．如图，已知二次函数c x ax y +-=42的图像经过点A （―1，0）和点D （5，0）． （1）求该二次函数的解析式；（2）直接写出该抛物线的对称轴及顶点C 的坐标；（3）点B 是该抛物线与y 轴的交点，求四边形ABCD21．如图，在△ABC 中，AC ＝40，BC ＝30，AB ＝50DEFG 的边EF 在AB 上，顶点D 、G 分别在AC 、BC 上．设EF ＝x ． （1）用含x 的代数式表示DE 的长；（2）当x 取什么值时，矩形DEFG 的面积最大？最大面积是多少？22．如图，足球场上守门员在O 开出一高球，球从离地面1米的A 处飞出（A 在y 轴上），运动员乙在距O 点6米的B 处发现球在自己头的正上方达到最高点M ，距地面约5米高，球落地后又一次弹起．据实验，足球在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半．（1）求足球开始飞出到第一次落地时，该抛物线的表达式． （2）足球第一次落地点C 距守门员多少米？（3）运动员乙要抢到第二个落点D ，他应再向前跑多少米？。

《二次函数》同步检测一、选择题（每题3分，共39分）1．二次函数y=x 2+2x －7的函数值是8，那么对应的x 的值是（ D ）A ．3B ．5C ．－3和5D ．3和－52、(2010三亚市月考).抛物线y=12x 2向左平移8个单位，再向下平移9个单位后，所得抛物线的表达式是（ A ）A. y=12(x+8)2-9 B. y=12(x-8)2+9 C. y=12(x-8)2-9 D. y=12(x+8)2+9 3、(2010年厦门湖里模拟)抛物线y =322+-x x 与坐标轴交点为 （ B ）A ．二个交点B ．一个交点C ．无交点D ．三个交点 4、若二次函数y=x 2－x 与y=－x 2+k 的图象的顶点重合，则下列结论不正确的是（ D ）A ．这两个函数图象有相同的对称轴B ．这两个函数图象的开口方向相反C ．方程－x 2+k=0没有实数根D ．二次函数y=－x 2＋k 的最大值为12 5、(2010年厦门湖里模拟)如图，抛物线)0(2>++=a c bx ax y 的对称轴是直线1=x ，且经过点P （3，0），则 的值为 ( A )A. 0B. －1C. 1D. 26、（2010年杭州月考）已知二次函数y ＝ax 2＋bx ＋c(a ≠0)的图象如图所示，给出以下结论：①0<abc ②当1x =时，函数有最大值。

③当13x x =-=或时，函数y 的值都等于0. ④024<++c b a 其中正确结论的个数是（ C ）A.1B.2C.3D.47、已知二次函数,2c bx ax y ++=且0,0>+-<c b a a ，则一定有（ A ）A ．042>-ac bB ．042=-ac bC ．042<-ac bD ．042≤-ac b 8、小敏在某次投篮中，球的运动路线是抛物线的一部分(如图)，若命中篮圈中心，则他与篮底的距离l 是( B ).A ．3.5mB ．4mC ．4.5mD ．4.6m9、（2010年西湖区月考）关于二次函数y =ax 2+bx+c 的图象有下列命题：①当c=0时，函数的图象经过原点；②当c ＞0时且函数的图象开口向下时，ax 2+bx+c=0必有两个不等实根；③函数图象最高点的纵坐标是ab ac 442-；④当b=0时，函数的图象关于y 轴对称.其中正确的个数是（ C ）A.1个 B 、2个 C 、3个 D. 4个10、（2009烟台市）二次函数2y ax bx c =++的图象如图所示，则一次函数24y bx b ac =+-与反比例函数a b cy x++=在同一坐标系内的图象大致为（ ）11、(2009年鄂州)已知=次函数y ＝ax 2+bx+c 的图象如图．则下列5个代数式：ac ，a+b+c ，4a －2b+c ，2a+b ，2a －b 中，其值大于0的个数为（ ） A ．2 B 3 C 、4 D 、512、（2009年兰州）在同一直角坐标系中，函数y mx m =+和函数xxxx222y mx x =-++（m 是常数，且0m ≠）的图象可能．．是13、（2009年黄石市）已知二次函数2y ax bx c =++的图象如图所示，有以下结论：①0a b c ++<；②1a b c -+>；③0abc >；④420a b c -+<；⑤1c a ->其中所有正确结论的序号是（ ） A ．①② B ． ①③④ C ．①②③⑤ D ．①②③④⑤二、填空题（每题3分，共30分）1、(2010三亚市月考)Y=-2(x-1)2 ＋5 的图象开口向 下 ，顶点坐标为 （1，5） ，当x ＞1时，y 值随着x 值的增大而 减小 。

九年级下册第二十六章二次函数水平测试题一、选择题（每小题3分，共36分）1、抛物线223yx 的顶点坐标是（）A.（－2，3）B.（2，3）C.（－2，－3） D.（2，－3）2、函数243y xx 化成2()ya xh k 的形式是（）A ．2(2)1y x B．2(2)1y x C ．2(2)7yx D ．2(2)7yx 3、二次函数362xkxy的图象与x 轴有交点，则k 的取值范围是（）A ．3k B ．03k k 且 C ．3k D．03kk且4、二次函数2(1)2y x 的最小值是（）A.2B ．2C ．1D ．15、对于抛物线21(5)33yx ，下列说法正确的是（）A ．开口向下，顶点坐标(53)，B ．开口向上，顶点坐标(53)，C ．开口向下，顶点坐标(53)，D ．开口向上，顶点坐标(53)，6、把抛物线2yx 向左平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为（）A. 2(1)3y x B. 2(1)3y x C.2(1)3yx D. 2(1)3yx 7.已知二次函数2(0)yaxbx c a 的图象如图所示，当0y 时，x 的取值范围是（）A ．13x B．3x C ．1xD ．3x或1x8、二次函数c bx ax y2的图象如图所示，则下列关系式不正确的是（）A 、a ＜0 B、abc ＞0xyO 31（7题图）..（8题图）C 、c b a ＞0D 、ac b 42＞09、若A （-4，y 1），B （-3，y 2），C （1，y 3）为二次函数y=x 2+4x-5的图象上的三点，则y 1，y 2，y 3的大小关系是（）A 、y 1＜y 2＜y 3B 、y 2＜y 1＜y 3 C、y 3＜y 1＜y 2 D 、y 1＜y 3＜y 210、若一次函数(1)y m x m 的图像过第一、三、四象限,则函数2ymxmx （）A 、有最大值4m B、有最大值4m C 、有最小值4m D 、有最小值4m 11、已知抛物线21y x x 与x 轴的一个交点为(0)m ，，则代数式22008m m 的值为（）A 、2006 B 、2007 C 、2008 D 、200912、函数2y ax b y axbx c 和在同一直角坐标系内的图象大致是（）二、填空题（每小题3分，共30分）13、二次函数322x xy 的图象的对称轴是直线。

第26章《二次函数》检测题（全卷共五个大题，满分150分，考试时间120分钟）抛物线)0(2≠++=a c bx ax y 的顶点坐标为)44,2(2ab ac ab --一、 选择题（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A 、B 、C 、D 的四个答案，其中只有一个是正确的，请将正确答案的代号填在答题卷中相应的位置上. 1．由二次函数1)3(22+-=x y ，可知（ ）A ．其图象的开口向下B ．其图象的对称轴为直线3-=xC ．其最小值为1D ．当3<x 时，y 随x 的增大而增大 2、k 为任何实数，则抛物线y ＝2(x ＋k)2－k 的顶点在（ ）上A 、直线y=x 上，B 、直线y= -xC 、x 轴D 、y 轴 3、0=+q p ，抛物线q px x y ++=2必过点（ ）A 、（-1，1）B 、（1，-1）C 、（-1，-1）D 、（1，1 ）4、已知点(3，1y ),(4，2y ), (5，3y )在函数y=2x 2+8x+7的图象上,则y 1,y 2,y 3的大小关系是( )A 、y 1>y 2>y 3B 、y 2> y 1> y 3C 、y 2>y 3> y 1D 、y 3> y 2> y 15．将抛物线23y x =向上平移3个单位，再向左平移2个单位，那么得到的抛物线的解析式为（ ）A ．23(2)3y x =++ B ．23(2)3y x =-+ C ．23(2)3y x =+- D ．23(2)3y x =--6、抛物线234y x x =--+与坐标轴的交点个数是（ ） A ． 0 B ． 1 C ． 2 D ． 37、若点(2，5)，(4，5)在抛物线y ＝ax 2＋bx ＋c 上，则它的对称轴是( )A ．ab x -= B ．x ＝1 C ．x ＝2 D ．x ＝38．二次函数c bx ax y ++=2的图象如右上图所示，则abc ，ac b 42-，b a +2，cb a ++这四个式子中，值为正数的有（ ）A ． 4个B ．3个C ．2个D ．1个9、如图是二次函数y=ax 2+bx+c 的部分图象，由图象可知不等式ax 2+bx+c ＜0的解集是（ ）A ． ﹣1＜x ＜5B ． x ＞5C ． x ＜﹣1且x ＞5D ． x ＜﹣1或x ＞510．已知二次函数y=ax 2+bx+c 的图象如图所示，它与x 轴的两个交点分别为（﹣1，0），（3，0）．对于下列命题：①b﹣2a=0；②abc＜0；③a﹣2b+4c ＜0；④8a+c＞0．其中正确的有（ ）卷相应位置的横线上． 11：抛物线422-+=x x y 的对称轴是________,顶点坐标是_________；12．已知二次函数2(0)y ax bx c a =++≠的顶点坐标(1, 3.2)--及部分图象（如图1所示），由图象可知关于x 的一元二次方程20ax bx c ++=的两个根分别是1 1.3x =和2x =。

第二十六章?二次函数?检测试题一、选择题〔每题3分，共30分〕1，二次函数y ＝(x －1)2+2的最小值是〔 〕A.－2B.2C.－1D.12，抛物线的解析式为y ＝(x －2)2＋1，那么抛物线的顶点坐标是〔 〕A.(－2,1)B.(2，1)C.(2，－1)D.(1，2)3，〔2021年芜湖市〕函数2y ax b y ax bx c =+=++和在同一直角坐标系内的图象大致是 〔 〕4，在一定条件下，假设物体运动的路程s 〔米〕与时间t 〔秒〕的关系式为s ＝5t 2+2t ，那么当t ＝4时，该物体所经过的路程为〔 〕A.28米B.48米C.68米D.88米5，二次函数y ＝ax 2+bx +c (a ≠0)的图象如图2所示，给出以下结论：① a +b +c ＜0；② a －b +c ＜0；③ b +2a ＜0；④ abc ＞0 .其中所有正确结论的序号是〔 〕A. ③④B. ②③C. ①④D. ①②③6，二次函数y ＝ax 2+bx +c 的图象如图3所示，假设M ＝4a +2b +c ，N ＝a －b +c ，P ＝4a +2b ，那么〔 〕A.M ＞0，N ＞0，P ＞0B. M ＞0，N ＜0，P ＞0C. M ＜0，N ＞0，P ＞0D. M ＜0，N ＞0，P ＜07，如果反比例函数y ＝k x 的图象如图4所示，那么二次函数y ＝kx 2－k 2x －1的图象大致为〔 〕图3 y x O 图4 y x O A ．y x O B ．y x O y x O 图5 x -11yO 图2 图18，用列表法画二次函数y ＝x 2+bx +c 的图象时先列一个表，当表中对自变量x 的值以相等间隔的值增加时，函数y 所对应的函数值依次为：20，56，110，182，274，380，506，650.其中有一个值不正确，这个不正确的值是( )A. 506B.380C.274D.189，二次函数y ＝x 2的图象向上平移2个单位，得到新的图象的二次函数表达式是〔 〕A. y ＝x 2－2B. y ＝(x －2)2C. y ＝x 2+2D. y ＝(x +2)210，如图6，小敏在今年的校运动会跳远比赛中跳出了满意一跳，函数h ＝3.5t －4.9t 2〔t 的单位：s ，h 的单位：m 〕可以描述他跳跃时重心高度的变化，那么他起跳后到重心最高时所用的时间是〔 〕A.0.71sB.0.70sC.0.63sD.0.36s二、填空题〔每题3分，共24分〕11，形如y ＝＿＿＿ (其中a ＿＿＿，b 、c 是_______ )的函数，叫做二次函数.12，抛物线y ＝(x –1)2–7的对称轴是直线 .13，如果将二次函数y ＝2x 2的图象沿y 轴向上平移1个单位，那么所得图象的函数解析式是 .14，平移抛物线y ＝x 2+2x －8，使它经过原点，写出平移后抛物线的一个解析式______ . 15，假设二次函数y ＝x 2－4x ＋c 的图象与x 轴没有交点，其中c 为整数，那么c ＝____(只要求写出一个).16，现有A 、B 两枚均匀的小立方体〔立方体的每个面上分别标有数字1，2，3，4，5，6〕.用小莉掷A 立方体朝上的数字为x 、小明掷B 立方体朝上的数字为y 来确定点P 〔x ，y 〕， 那么它们各掷一次所确定的点P 落在抛物线y ＝－x 2+4x 上的概率为＿＿＿.17，二次函数y ＝ax 2+bx +c 的图像如图7所示，那么点A (a ，b )在第＿＿＿象限.18，抛物线y ＝x 2－6x +5的局部图象如图8，那么抛物线的对称轴为直线x ＝ ，满足y ＜0的x 的取值范围是 .三、解答题〔共66分〕19，抛物线y ＝ax 2经过点(1，3)，求当y ＝4时，x 的值.20，一抛物线与x 轴的交点是)0,2( A 、B 〔1，0〕，且经过点C 〔2，8〕。

九年级下册第二十六章二次函数整章水平测试题一、选择题（每小题3分，共24分） 1.抛物线2(1)3y x =-+的对称轴是（ ） （A ）直线1x =（B ）直线3x =（C ）直线1x =-（D ）直线3x =-2．（2008齐齐哈尔）对于抛物线21(5)33y x =--+，下列说法正确的是（ ）（A ）开口向下，顶点坐标(53)， （B ）开口向上，顶点坐标(53)，（C ）开口向下，顶点坐标(53)-，（D ）开口向上，顶点坐标(53)-，3.若A （1,413y -），B （2,45y -），C （3,41y ）为二次函数245y x x =+-的图象上的三点，则1,y 2,y 3y 的大小关系是( ) （A ）123y y y <<（B ）213y y y << （C ）312y y y << （D ）132y y y <<4.二次函数362+-=x kx y 的图象与x 轴有交点，则k 的取值范围是【 】 （A ）3<k （B ）03≠<k k 且 （C ）3≤k （D ）03≠≤k k 且5.（20082（ ）（Ａ）243y x x =-+（Ｂ）234y x x =-+（Ｃ）233y x x =-+ （Ｄ）248y x x =-+6．烟花厂为扬州418烟花三月经贸旅游节特别设计制作一种新型礼炮，这种礼炮的升空高度(m)h 与飞行时间(s)t的关系式是252012h t t =-++，若这种礼炮在点火升空到最高点处引爆，则从点火升空到引爆需要的时间为（ ） （Ａ）3s （Ｂ）4s（Ｃ）5s （Ｄ）6s7.（2008泰安）如图所示是二次函数2122y x =-+的图象在x 轴上方的一部分，对于这段图象与x 轴所围成的阴影部分的面积，你认为与其最．接近的值是（ ） （A ）4 （B ）163（C ）2π（D ）88.如图，某厂有许多形状为直角梯形的铁皮边角料，为节约资源，现要按图中所示的方法从这些边角料上截取矩形（阴影部分）铁皮备用，当截取的矩形面积最大时，矩形两边长x y ，应分别为（ ） （A ）1014x y ==， （B ）1410x y ==， （C ）1215x y ==，（D ）1512x y ==，二、填空题（每小题3分，共24分）9.（2008太原）抛物线2243y x x =-+的顶点坐标是 ．10.平移抛物线228y x x =+-，使它经过原点，写出平移后抛物线的一个解析式 .11.已知两条抛物线：y ＝x 2＋2x －3和y ＝2x 2＋x －3，请写出它们的一条共同点 .12.将(21)(2)1y x x =-++化成()y a x m n 2=++的形式为 . 13.某商店经营一种水产品，成本为每千克40元的水产品，据市场分析，若按每千克50元销售，一个月能售出500千克；销售价每涨1元，月销售量就减少10千克，针对这种水产品的销售情况，销售单价定为 元时，获得的利润最多.14.已知二次函数2y ax bx c =++的图象如图所示，则点()P a bc ，在第象限．15．已知二次函数2y ax bx c =++（a b c ，，是常数），x 与y 的部分对应值如下表，则当x 满足的条件是 时，0y =；当x 满足的条件是 时，0y >．x2-1- 0 1 2 3y16- 6-26-16.廊桥是我国古老的文化遗产．如图，是某座抛物线型的廊桥示意图，已知抛物线的函数 表达式为211040y x =-+，为保护廊桥的安全，在该抛物线上距水面AB 高为8米的点E 、 F 处要安装两盏警示灯，则这两盏灯的水平距离EF 是 米（精确到1米）．三、解答题（共52分）yO17.已知一抛物线与x 轴的交点是)0,2(-A 、B （1，0），且经过点C （2，8）。

反比例函数１。

反比例函数y ＝x3-k 的图象，当x ＞0时，y 随x 的增大而增大，则k 的取值范围是（ ） （A ）k ＜3 （B ）k ≤3 （C ）k ＞3 （D ）k ≥3 答案：A 2．已知：正比例函数y=k 1x 的图象与反比例函数xk y 2=(x>0)的图象交于点M （a,1）， MN ⊥x 轴于点N （如图），若△OMN 的面积等于2，求这两个函数的解析式. 解：∵MN ⊥x 轴，点M （a ，1） ∴S △OMN=a 21=2 ∴a=4 ∴M(4,1)∵正比例函数y=k 1x 的图象与反比例函数xk y 2=(x>0)的 图象交于点M （4,1）∴ 414121k k == 解得44121==∴正比例函数的解析式是x y 41=，反比例函数的解析式是 3． 不在函数xy 12=图像上的点是 （ ） A ．（2,6） B.（-2，-6） C.（3,4） D.（-3,4） 答案：D 4．如图，在第一象限内,点P,M ()2,a 是双曲线)0(≠=k xky 上的两点,PA ⊥x 轴于点A,MB ⊥x 轴于点B,PA 与OM 交于点C,则△OAC 的面积 为 .答案：345．反比例函数xy 6=图象上有三个点)(11y x ，，)(22y x ，，)(33y x ，，其中3210x x x <<<， 则1y ，2y ，3y 的大小关系是( )A ．321y y y <<B ．312y y y <<C ．213y y y <<D ．123y y y <<答案：B 6．函数xy 1-=的自变量x 的取值范围是 ． 答案：0≠x图27.如图2，所示的计算程序中，y 与x 之间的函数关系对应的图象所在的象限是（ C ）A. 第一象限B. 第一、三象限C. 第二、四象限D. 第一、四象限 8．若反比例函数ky x=的图象经过点（－3，2），则k 的值为 （ A ）． A ．－6 B ．6 C ．-5 D ．59. 函数y ＝x -2＋31-x 中自变量x 的取值范围是A ．x ≤2B ．x ＝3C ．x ＜2且x ≠3D ．x ≤2且x ≠3答案 A 10．如图，已知梯形ABCO 的底边AO 在x 轴上，BC ∥AO ，AB ⊥AO ，过点C 的双曲线k y x=交OB 于D ，且OD ：DB=1 ：2，若△OBC 的面积等于3，则k 的值（）A ． 等于2B ．等于34C ．等于245D ．无法确定答案 B11. 已知点（-1，1y ），（2，2y ），（3，3y ）在反比例函数x k y 12--=的图像上. 下列结论中正确的是（ ） A ．321y y y >> B ．231y y y >> C ．213y y y >> D ． 132y y y >>答案B12． 已知：y ＝y 1＋y 2，y 1与x 2成正比例，y 2与x 成反比例，且x ＝1时，y ＝3；x ＝-1时，y ＝1. 求x ＝-21时，y 的值．解：解：y 1与x 2成正比例，y 2与x 成反比例设y 1＝k 1x 2，y 2＝x k 2，y ＝k 1x 2＋x k 2…………………………………………………2分把x ＝1，y ＝3，x ＝-1，y ＝1分别代入上式得 ⎩⎨⎧-=+=212113k k k k ……………………3分∴x x y k k 12,12221+=⎩⎨⎧== …………………………………………5分当x ＝-21, y ＝2×(-21)2＋211-＝21-2＝-23 ………………………………6分13.（本题满分9分）如图，P 1是反比例函数)0(＞k x ky =在第一象限图像上的一点，点A 1 的坐标为(2，0)． （1）当点P 1的横坐标逐渐增大时，△P 1O A 1的面积 将如何变化？（2）若△P 1O A 1与△P 2 A 1 A 2均为等边三角形，求 此反比例函数的解析式及A 2点的坐标．第25题图答案：（1）解：（1）△P 1OA 1的面积将逐渐减小． …………………………………2分 （2）作P 1C ⊥OA 1，垂足为C ，因为△P 1O A 1为等边三角形， 所以OC=1，P 1C=3，所以P 1)3,1(． ……………………………………3分代入xk y =，得k=3，所以反比例函数的解析式为x y 3=． ……………4分作P 2D ⊥A 1 A 2，垂足为D 、设A 1D=a ，则OD=2+a ，P 2D=3a ，所以P 2)3,2(a a +． ……………………………………………………………6分代入xy 3=，得33)2(=⋅+a a ，化简得0122=-+a a解的：a=-1±2 ……………………………………………7分 ∵a ＞0 ∴21+-=a………………………………8分所以点A 2的坐标为﹙22，0﹚ ………………………………………………9分14．函数y ＝1x ＋2中自变量的取值范围是___________． 答案2x ≠-15．已知反比例函数y ＝ kx的图象与二次函数y ＝ax 2＋x －1的图象相交于点（2，2） （1）求a 和k 的值；（2）反比例函数的图象是否经过二次函数图象的顶点，为什么？答案 因为二次函数21y ax x =+-与反比例函数ky x=交于点（2，2）所以2=4a+2-1，解得14a = (2)分所以k=4 ........................................................................................................4分（2）反比函数的图像经过二次函数图像的顶点 ............................................5分由（1）知，二次函数和反比例函数的关系式分别是 2114y x x =+-和 4y x= 因为[]222221111(44)(448)44411(2)8(2)244y x x x x x x x x =+-=+-=++-=+-=+-................6分所以二次函数图像的顶点坐标是（-2,-2）...........................................................7分因为x =-2时，422y ==--所以反比例函数图像经过二次函数图像的顶点........8分 16．已知反比例函数y ＝1x，下列结论不正确．．．的是（ ） A ．图象经过点（1，1） B ．图象在第一、三象限C ．当x ＞1时，0＜y ＜1D ．当x ＜0时，y 随着x 的增大而增大 17. 已知点P 的坐标为（m ，0），在x 轴上存在点Q （不与P 点重合），以PQ 为边作正方形PQMN ，使点M 落在反比例函数y = 2x-的图像上.小明对上述问题进行了探究，发现不论m取何值，符合上述条件的正方形只有．．两个，且一个正方形的顶点M 在第四象限，另一个正方形的顶点M 1在第二象限.（1）如图所示，若反比例函数解析式为y = 2x-，P 点坐标为（1， 0），图中已画出一符合条件的一个正方形PQMN ，请你在图中画出符合条件的另一个正方形PQ 1M 1N 1， 并写出点M 1的坐标；M 1的坐标是（2） 请你通过改变P 点坐标，对直线M 1 M 的解析式y ﹦kx ＋b 进行探究可得 k ﹦ ， 若点P 的坐标为（m ，0）时，则b ﹦ ；（3） 依据(2)的规律，如果点P 的坐标为（6，0），请你求出点M 1和点M 的坐标． 解：（1）如图；M 1 的坐标为（－1，2） ……2分（2）1-=k ，m b = …………………4分（各2分） （3）由（2）知，直线M 1 M 的解析式为6+-=x y 则M (x ，y )满足2)6(-=+-⋅x x解得1131+=x ，1132-=x ∴ 1131-=y ，1132+=y(第23题∴M 1，M 的坐标分别为（113-，113+），（113+，113-）．……………4分18．（如左下图）已知反比例函数1my x-=的图象如图，则m 的取值范围是 ．答案：m <119．（如右上图）反比例函数)0(1>-=x xy 的图象如图１所示，随着x 值的增大，y 值（ ） A ．增大 B ．减小 Ｃ．不变 Ｄ．先增大后减小答案：A 20．已知函数xy 6-=，当2-=x 时，y 的值是______． 答案：321．如图，一次函数y ax b =+的图象与x与反比例函数k y x=的图象相交于C ，D 点作y 轴，x 轴的垂线，垂足为E ，F 有下列四个结论： ①△CEF 与△DEF 的面积相等； ②③△DCE ≌△CDF ； ④其中正确的结论是 ．22. （2010经过A （1，2）、B （2，b ）两点. （1）求双曲线的解析式；（2）试比较b 与2的大小.答案：解：（1）因为点A （1，2）在函数y =k x上k =2,所以双曲线的解析式为2y x=； （2）由函数2y x=的性质可得在第一象限y 随x 第13题图图1数图象上求出b 的值，从而比较b 与2的大小）23．如图，正比例函数12y x =的图象与反比例函数k y x =(0)k ≠在第一象限的图象交于A点，过A 点作x 轴的垂线，垂足为M ，已知OAM∆的面积为1.（1）求反比例函数的解析式；（2）如果B 为反比例函数在第一象限图象上的点（点B 与点A 不重合），且B 点的横坐标为1，在x 轴上求一点P ，使PA PB +最小.答案．解：（1） 设A 点的坐标为（a ，b ），则kb a=.∴ab k =.∵112ab =,∴112k =.∴2k =. ∴反比例函数的解析式为2y x=. ············································ 3分(2) 由212y xy x ⎧=⎪⎪⎨⎪=⎪⎩得2,1.x y =⎧⎨=⎩ ∴A 为（2，1）. ································· 4分 设A 点关于x 轴的对称点为C ，则C 点的坐标为（2，1-）.令直线BC 的解析式为y mx n =+.∵B 为（1，2）∴2,12.m n m n =+⎧⎨-=+⎩∴3,5.m n =-⎧⎨=⎩∴BC 的解析式为35y x =-+. ··············································· 6分当0y =时，53x =.∴P 点为（53，0）. 24．如图，已知反比例函数ky x=与一次函数y x b =+的图象在第一象限相交于点(1,4)A k -+． （1）试确定这两个函数的表达式；（2）求出这两个函数图象的另一个交点B的坐标，并根据图象xA (第20题)写出使反比例函数的值大于一次函数的值的x 的取值范围．答案：.解：（1）∵已知反比例函数ky x=经过点(1,4)A k -+，∴41kk -+=，即4k k -+= ∴2k=∴A(1，2) ∵一次函数y x b =+的图象经过点A(1，2)，∴21b =+ ∴1b=∴反比例函数的表达式为2y x=， 一次函数的表达式为1y x =+。