【复习指导】2020-2021学年高中数学奥林匹克竞赛训练题(199)(无答案)

2020年中国数学奥林匹克试题和详细解答word 版一、给定锐角三角形PBC ，PC PB ≠．设A ，D 分不是边PB ，PC 上的点，连接AC ，BD ，相交于点O. 过点O 分不作OE ⊥AB ，OF ⊥CD ，垂足分不为E ，F ，线段BC ，AD 的中点分不为M ，N ．〔1〕假设A ，B ，C ，D 四点共圆，求证：EM FN EN FM ⋅=⋅；〔2〕假设 EM FN EN FM ⋅=⋅，是否一定有A ，B ，C ，D 四点共圆？证明你的结论．解〔1〕设Q ，R 分不是OB ，OC 的中点，连接EQ ，MQ ，FR ，MR ，那么11,22EQ OB RM MQ OC RF ====，又OQMR 是平行四边形，因此OQM ORM ∠=∠，由题设A ，B ，C ，D 四点共圆，因此ABD ACD ∠=∠，因此 图1 22EQO ABD ACD FRO ∠=∠=∠=∠，因此 EQM EQO OQM FRO ORM FRM ∠=∠+∠=∠+∠=∠， 故 EQM MRF ∆≅∆， 因此 EM ＝FM ， 同理可得 EN ＝FN ， 因此 EM FN EN FM ⋅=⋅．〔2〕答案是否定的．当AD ∥BC 时，由于B C ∠≠∠，因此A ，B ，C ，D 四点不共圆，但现在仍旧有EM FN EN FM ⋅=⋅，证明如下：如图2所示，设S ，Q 分不是OA ，OB 的中点，连接ES ，EQ ，MQ ，NS ，那么11,22NS OD EQ OB ==，CB因此NS ODEQ OB=．①又11,22ES OA MQ OC==，因此ES OAMQ OC=．②而AD∥BC，因此OA ODOC OB=，③由①，②，③得NS ES EQ MQ=．因为2NSE NSA ASE AOD AOE∠=∠+∠=∠+∠，()(1802) EQM MQO OQE AOE EOB EOB∠=∠+∠=∠+∠+︒-∠(180)2AOE EOB AOD AOE=∠+︒-∠=∠+∠，即NSE EQM∠=∠，因此NSE∆～EQM∆，故EN SE OAEM QM OC==〔由②〕．同理可得，FN OAFM OC=，因此EN FN EM FM=，从而EM FN EN FM⋅=⋅．CB二、求所有的素数对〔p ，q 〕，使得q p pq 55+．解：假设pq |2，不妨设2=p ，那么q q 55|22+，故255|+q q ．由Fermat 小定理， 55|-q q ，得30|q ，即5,3,2=q ．易验证素数对)2,2(不合要求，)3,2(，)5,2(合乎要求．假设pq 为奇数且pq |5，不妨设5=p ，那么q q 55|55+，故6255|1+-q q ． 当5=q 时素数对)5,5(合乎要求，当5≠q 时，由Fermat 小定理有15|1--q q ，故626|q ．由于q 为奇素数，而626的奇素因子只有313，因此313=q ．经检验素数对)313,5(合乎要求．假设q p ,都不等于2和5，那么有1155|--+q p pq ，故)(m od 05511p q p ≡+--． ①由Fermat 小定理，得 )(m od 151p p ≡- ， ② 故由①，②得)(m od 151p q -≡-． ③设)12(21-=-r p k ，)12(21-=-s q l ， 其中s r l k ,,,为正整数． 假设l k ≤，那么由②，③易知)(mod 1)1()5(5)5(1112121)12)(12(2)12(21)12(2p r r q s r s p s lkl kl -≡-≡==≡=----------，这与2≠p 矛盾！因此l k >．同理有l k <，矛盾！即现在不存在合乎要求的),(q p ． 综上所述，所有满足题目要求的素数对),(q p 为)3,2(，)2,3(，)5,2(，)2,5(，)5,5(，)313,5(及)5,313(．三、设m ，n 是给定的整数，n m <<4，1221+n A A A 是一个正2n +1边形，{}1221,,,+=n A A A P ．求顶点属于P 且恰有两个内角是锐角的凸m 边形的个数．解 先证一个引理：顶点在P 中的凸m 边形至多有两个锐角，且有两个锐角时，这两个锐角必相邻．事实上，设那个凸m 边形为m P P P 21，只考虑至少有一个锐角的情形，现在不妨设221π<∠P P P m ，那么)13(2122-≤≤>∠-=∠m j P P P P P P m m j ππ，更有)13(211-≤≤>∠+-m j P P P j j j π．而321P P P ∠+11P P P m m -∠>π，故其中至多一个为锐角，这就证明了引理． 由引理知，假设凸m 边形中恰有两个内角是锐角，那么它们对应的顶点相邻． 在凸m 边形中，设顶点i A 与j A 为两个相邻顶点，且在这两个顶点处的内角均为锐角．设i A 与j A 的劣弧上包含了P 的r 条边〔n r ≤≤1〕，如此的),(j i 在r 固定时恰有12+n 对．〔1〕 假设凸m 边形的其余2-m 个顶点全在劣弧j i A A 上，而j i A A 劣弧上有1-r 个P 中的点，现在那个2-m 顶点的取法数为21--m r C ．〔2〕 假设凸m 边形的其余2-m 个顶点全在优弧j i A A 上，取i A ，j A 的对径点i B ，j B ，由于凸m 边形在顶点i A ，j A 处的内角为锐角，因此，其余的2-m 个顶点全在劣弧j i B B 上，而劣弧j i B B 上恰有r 个P 中的点，现在那个2-m 顶点的取法数为2-m r C ．因此，满足题设的凸m 边形的个数为))()()(12()12()()12(11111111121211221∑∑∑∑∑==--+---=-=--=----+-+=⎪⎭⎫⎝⎛++=++nr nr m rm r m r m r n r m r n r m r nr m rm r C C C C n C C n CCn))(12(111--+++=m nm n C C n ．四、给定整数3≥n ，实数n a a a ,,,21 满足 1m in 1=-≤<≤j i nj i a a ．求∑=nk k a 13的最小值．解 不妨设n a a a <<< 21，那么对n k ≤≤1，有k n a a a a k k n k n k 2111-+≥-≥++-+-，因此()∑∑=-+=+=nk kn knk ka a a13131321()()()∑=-+-+-+⎪⎭⎫ ⎝⎛++-+=n k k n k kn k k n k a a a a a a 121211414321 ()∑∑==-+-+≥+≥n k nk kn k k n a a 13131218181． 当n 为奇数时，222113313)1(412221-=⋅⋅=-+∑∑-==n i k n n i nk ． 当n 为偶数时，32113)12(221∑∑==-=-+n i nk i kn⎪⎪⎪⎭⎫ ⎝⎛-=∑∑==21313)2(2ni n j i j)2(4122-=n n ． 因此，当n 为奇数时，2213)1(321-≥∑=n a nk k，当n 为偶数时，)2(3212213-≥∑=n n a nk k ，等号均在n i n i a i ,,2,1,21=+-=时成立． 因此，∑=nk k a 13的最小值为22)1(321-n 〔n 为奇数〕，或者)2(32122-n n 〔n 为偶数〕．五、凸n 边形P 中的每条边和每条对角线都被染为n 种颜色中的一种颜色．咨询：对如何样的n ，存在一种染色方式，使得关于这n 种颜色中的任何3种不同颜色，都能找到一个三角形，其顶点为多边形P 的顶点，且它的3条边分不被染为这3种颜色？ 解 当n 3≥为奇数时，存在合乎要求的染法；当n 4≥为偶数时，不存在所述的染法。

数学奥林匹克高中训练题（一）第一试一、选择题（本题满分36分，每小题6分）1．(训练题22)集合111{|log 2,}23nn n N -<<-∈的真子集的个数是(A)． (A) 7 (B)8 (C)31 (D)322．(训练题22)从1到9这九个自然数中任取两个，分别作为对数的真数和底数，共得不同的对数值(B)．(A) 52个 (B) 53个 (C) 57个 (D) 72个3．(训练题22)空间有四张不同的平面，则这四张平面可能形成的交线条数取值的集合是(C)．(A){1,2,3,4,5,6} (B) {0,1,2,3,4,5,6} (C) {0,1,3,4,5,6} (D) {0,1,2,3,5,6}4．(训练题22) 函数(),()y f x y g x ==的定义域及值域都是R ，且都存在反函数，则11((()))y f g f x --=的反函数是(B)．(A)1((()))y f g f x -= (B) 1((()))y f g f x -= (C) 11((()))y f g f x --= (D) 11((()))y f g f x --=5．(训练题22) 若cos 40sin 40o o ω=+,则1239239ωωωω-++++等于(D)． (A)1cos 2018o (B) 1sin 409o (C) 1cos 409o (D) 2sin 209o 6．(训练题22) 当01x <<时，222sin sin sin ,(),x x x x x x的大小关系是(B)． (A) 222sin sin sin ()x x x x x x << (B) 222sin sin sin ()x x x x x x << (C) 222sin sin sin ()x x x x x x << (D) 222sin sin sin ()x x x x x x<< 二、填空题（本题满分54分，每小题9分）1．(训练题22) 已知211(),()5,()2f x x g x x g x -==-+表示)(x g 的反函数，设11()(())(())F x f g x g f x --=-．则()F x 的最小值是 703． 2．(训练题22) 在1000和9999之间由四个不同数字组成，且个位数字与千位数字之差的绝对值是2的整数共有 840 个．3．(训练题22) 四面体P ABC -中，,8,6,9,120o PC ABC AB BC PC ABC ⊥===∠=面，则二面角B AP C --的余弦值是 ． 4．(训练题22) 设{}P =不少于3的自然数，在P 上定义函数f 如下：若,()n P f n ∈表示不是n 的约数的最小自然数，则(360360)f = 16 ．5．(训练题22)n 为不超过1996的正整数，如果有一个θ，使(sin cos )sin cos ni n i n θθθθ+=+成立，则满足上述条件的n 值共有 498 个．6．(训练题22)在自然数列中由1开始依次按如下规则将某些数染成红色．先染1；再染两个偶数2,4；再染4后最邻近的三个连续奇数5，7，9；再染9后最邻近的四个连续偶数10，12，14，16；再染此后最邻近的五个连续奇数17，19，21，23，25，按此规则一直染下去，得一红色子列1，2，4，5，7，9，10，12，14，16，17，…，则红色子列中由1开始数起的第1996个数是 3929 ． 第二试一、(训练题22)(本题满分25分) 点M 是正三角形内一点，证明：由线段,MA MB 和MC 为边组成的三角形面积不超过原正三角形面积的13． 二、(训练题22)(本题满分25分) 若21x y +≥，试求函数2224u y y x x =-++的最小值．95- 三、(训练题22)(本题满分35分) 证明：从任意四个正整数中一定可以选出两个数x 和y ，使得如下不等式成立0212x y x y xy-≤<+++． 四、(训练题22)(本题满分35分)连结圆周上九个不同点的36条弦要么染成红色，要么染成蓝色，我们称它们为“红边”或“蓝边”，假定由这九个点中每三个点为顶点的三角形中都含有“红边”，证明：这九个点中存在四个点，两两连结的六条边都是红边．数学奥林匹克高中训练题（二）第一试一、选择题（本题满分36分，每小题6分）1．(训练题23)119963+除以19971996⨯所得的余数是(D)．(A) 1 (B) 1995 (C) 1996 (D) 19972．(训练题23)若在抛物线)0(2>=a ax y 的上方可作一个半径为r 的圆与抛物线相切于原点O ，且该圆与抛物线没有别的公共点，则r 的最大值是(A)． (A)a 21 (B)a1 (C)a (D)a2 3．(训练题23)考虑某长方体的三个两两相邻的面上的三条对角线及体对角线（共四条线段），则正确的命题是(B)．(A)必有某三条线段不能组成一个三角形的三边．(B)任何三条线段都可组成一个三角形，其中每个内角都是锐角．(C)任何三条线段都可组成一个三角形，其中必有一个是钝角三角形．(D)任何三条线段都可组成一个三角形，其形状是“锐角的”或者是“非锐角的”，随长方体的长，宽，高而变化，不能确定．4．(训练题23)若20π<<x ，则11tan cot sin cos x x x x++-的取值范围是(D)． (A)()+∞∞-, (B)()+∞,0 (C)),21(+∞ (D)()+∞,1 5．(训练题23)有5个男孩与3个女孩站成一排照相任何两个女孩都不相邻，则其可能的排法个数是(A)． (A)!5!7!8⋅ (B)!4!6!7⋅ (C) !7!3!10⋅ (D) !3!7!10⋅ 6．(训练题23)使得11cos 51sin +>n 成立的最小正整数n 是(B)．(A)4 (B)5 (C)6 (D)7二、填空题（本题满分54分，每小题9分）1．(训练题23)设R a ∈，若函数310),(+==xy x f y 关于直线x y =对称，且)(x f y =与)lg(2a x x y +-=有公共点，则a 的取值范围是 6a <- ．2．(训练题23)设1,,2-=∈+i R b a 且存在C z ∈，适合⎪⎩⎪⎨⎧≤+=+1z bi a z z z 则ab 的最大值等于 18 ． 3．(训练题23)设 900<<α，若ααsin 1)60tan(31=-+ ，则α等于 3050o o 或 ． 4．(训练题23)设''''D C B A ABCD -是棱长为1的正方体，则上底面ABCD 的内切圆上的点P 与过顶点'''',,,D C B A 的圆上的点Q 之间的最小距离=d2 ． 5．(训练题23)如图，在直角坐标系xOy 中，有一条周期性折线（函数）).(:1x f y l =现把该曲线绕原点O 按逆时针方向旋转45得到另一条曲线2l ，则这两条曲线与y 轴及直线()N n n x ∈=围成的图形的面积等于(12n +-- ．6．(训练题23)设b a ,都是正整数，且100)21(2+=+b a 则b a ⋅的个位数等于 4 ．第二试一、(训练题23)(本题满分25分) 求证：在复平面上，点集}01:{3=++∈=z z C z S 中，除去某一个点外的所有的点都在圆环45313<<z 中． 二、(训练题23)(本题满分25分)已知抛物线),0(22>=p px y 其焦点为F .试问：是否存在过F 点的弦AB （B A ,均在抛物线上，且A 在第一象限内），以及y ）轴正半轴上的一点P ，使得B A P ,,三点构成一个以P 为直角顶点的等腰直角三角形？证实你的回答.如果回答是肯定的，请求出直线AB 的方程．)2p y x =- 三、(训练题23)(本题满分35分)平面上给定321A A A ∆及点0P ，构造点列0P ，1P ， 2P ，使得13+k P 为点k P 3绕中心1A 顺时针旋转150时所到达的位置，而23+k P 和33+k P 为点13+k P 和23+k P 分别绕中心2A 和3A 顺时针旋转 105时所到达的位置， ,3,2,1,0=k .若对某个N n ∈，有03P P n =，试求321A A A ∆的各个内角的度数及三个顶点321,,A A A 的排列方向．四、(训练题23)(本题满分35分)设n ααα≤≤≤< 210，n b b b ≤≤≤< 210，且∑∑==≥n i i n i i b a 11又存在)1(n k k ≤≤使得当k i ≤时有i i a b ≤，当k i >时，有i i a b >.求证：∏∏==≥n i i n i ib a 11． 1。

数学奥林匹克高中训练题(143)注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）请点击修改第I 卷的文字说明第II 卷（非选择题）一、填空题1.已知正实数a 、b 、c 满足(1+a )(1+b )(1+c )=8.则abc +9abc的最小值是_________.2.设O 是锐角ΔABC 所在平面内一点（在ΔABC 外），CD⊥AB 于点D .若OA⃑⃑⃑⃑⃑⃑⃑ =a ⃑⃑ ,OB ⃑⃑⃑⃑⃑⃑⃑ =b ⃑⃑ ,OC ⃑⃑⃑⃑⃑⃑⃑ =c ⃑ ，则OD ⃑⃑⃑⃑⃑⃑⃑ =_________（用a ⃑⃑ ,b ⃑⃑ ,c ⃑ 表示）. 3.函数f (x )=|sinx +12sin2x|(x ∈R )的值域是_________.4.已知有限项等差数列{a n }的首项a 1=1，公差为2，其所有项的算术平均值是2011.若从中删去一项后，该数列剩余各项的算术平均值为整数.则删项的方法有_________种. 5.如图，梯形ABCD （AB∥CD ∥y 轴，|AB |>|CD |）内接于椭圆x 2a 2+y2b2=1(a >b >0)，是对角线AC 与的BD 交点.记|AB |=m ，|CD |=n ，|OE |=d .则m−nd的最大值为_________.6.某人练习打靶，开始时，他距靶100m ，此时，进行第一次射击.若此次射击不中，则后退50m 进行第二次射击，一直进行下去.每次射击前都后退50m ，直到命中为止，已知他第一次的命中率为14，且命中率与距离的平方成反比.则他能够命中的概率等于_________. 7.如图，已知平面α上的ΔABC 与ΔA 1B 1C 1分别在直线l 的两侧，它们与l 没有公共点，并且关于直线l 对称.现将平面α沿直线l 折成一个直二面角，则六个点A 、B 、C 、A 1、B 1、C 1可以确定_________个平面（用数字作答）.8.复数列z 0,z 1,⋅⋅⋅满足|z 0|=1，z n+1=n z.若z 2011=1，则z 0可以有_________种取值.二、解答题9.已知+，方程−2ax −2alnx =0在(0,+∞)上有唯一解.求a 的值.10.给定正整数n (n≥3)，a n =(1.0·02·)n（即a n 等于n 进制表示为1.0·02·的数）.试求lim n→∞1n (1a3+1a 3a 4+⋅⋅⋅+1a3a 4⋅⋅⋅a n)的值. 11.在椭圆G 外一直线l 上取n (n ∈N +,n ≥2)个不同的点P 1,P 2,⋅⋅⋅,P n ，过P i (1≤i ≤n )向椭圆G 作切线PA i 、PB i ，切点分别为A i 、B i .记直线A i B i 为l i .（1）若存在正整数j 、i （1≤j 、i ≤n ，j ≠i ），使得点P i 在直线l j 上，证明：点P j 在直线l i 上；（2）试求直线l 1,l 2,⋅⋅⋅,l n 将椭圆G 分成的区域的个数.12.如图，ΔABC 内接于圆Γ，D 是劣弧BC 的中点，圆Γ1与圆Γ切于点D ，与边BC 切于点E .过点A 作圆Γ1的切线AP ，切点为P .证明：AB +AC =2AP .13.己知正实数x 、y 、z 满足(x +y +z )3=32xyz ，试求f (x,y,z )=x 4+y 4+z 4(x+y+z )4的最大值和最小值.14.证明：存在无穷多组正整数组(a,b,c,d )，满足： （1）a>c >0，且(a,c )=1；（2）a 可以有无穷多个取值； （3）恰存在22011个正整数n 使得(an +b )|(cn +d ) .15.某公司印制了一批文化衫，每件文化衫可有红、黄、蓝三种不同的颜色和四种不同的图案.现将这批文化衫分发给n名新员工，每名员工恰好分到图案不同的4件.试求n的最小值，使得总存在两个人，他们所分到的某两种图案的4件文化衫的颜色全部相同.参考答案1.10【解析】1. 由8=(1+a )(1+b )(1+c )≥2√a ⋅2√b ⋅2√c =8√abc ⇒abc ≤1.当且仅当a=b =c =1时，上式等号成立.容易验证，函数f (x )=x +9x在(0,3)上是减函数.而0<abc ≤1<3，故当abc =1时，f (abc )=abc +9abc最小，且最小值为10.故答案为：102.a ⃑⃑ +(c ⃑ −a ⃑⃑ )(b ⃑ −a ⃑⃑ )|b ⃑−a⃑⃑ |(b ⃑⃑ −a ⃑⃑ )【解析】2.由AC ⃑⃑⃑⃑⃑⃑ ⋅AB ⃑⃑⃑⃑⃑⃑⃑ =|AC |⃑⃑⃑⃑⃑⃑⃑⃑⃑⃑ |AB |⃑⃑⃑⃑⃑⃑⃑⃑⃑⃑ cosA =|AB |⃑⃑⃑⃑⃑⃑⃑⃑⃑⃑ |AD |⃑⃑⃑⃑⃑⃑⃑⃑⃑⃑ ，得|AD |⃑⃑⃑⃑⃑⃑⃑⃑⃑⃑ =AC ⃑⃑⃑⃑⃑⃑ ⋅AB ⃑⃑⃑⃑⃑⃑⃑ |AB |⃑⃑⃑⃑⃑⃑⃑⃑⃑⃑ .则AD ⃑⃑⃑⃑⃑⃑⃑ =(|AD |⃑⃑⃑⃑⃑⃑⃑⃑⃑⃑ |AB |⃑⃑⃑⃑⃑⃑⃑⃑⃑⃑ )AB ⃑⃑⃑⃑⃑⃑⃑ =(AC ⃑⃑⃑⃑⃑⃑ ⋅AB ⃑⃑⃑⃑⃑⃑⃑ |AB |⃑⃑⃑⃑⃑⃑⃑⃑⃑⃑ 2)AB ⃑⃑⃑⃑⃑⃑⃑ . 故OD ⃑⃑⃑⃑⃑⃑⃑ =OA ⃑⃑⃑⃑⃑⃑⃑ +AD ⃑⃑⃑⃑⃑⃑⃑ = a ⃑⃑ +(c ⃑ −a ⃑⃑ )(b ⃑ −a ⃑⃑ )|b ⃑−a⃑⃑ |(b ⃑⃑ −a ⃑⃑ ). 故答案为：a ⃑⃑ +(c ⃑ −a ⃑⃑ )(b ⃑ −a ⃑⃑ )|b ⃑−a⃑⃑ |(b ⃑⃑ −a ⃑⃑ ) 3.[0,3√34]【解析】3. 显然，f (0)=0，f (x )≥0.从而，f (x )的最小值是0. 下面求f (x )的最大值. 注意到f (x )=|sinx +12sin2x|=|(1+cosx )sinx |=|2cos 2x 2⋅2sin x 2⋅cos x 2|=4|sin x 2⋅cos 3x 2|=4√27sin 2x 2⋅13cos 2x 2⋅13cos 2x 2⋅13cos 2x2≤4√27(sin 2x 2+cos 2x 24)4=3√34.当且仅当sin2x 2=13cos 2x 2，即x =2kπ±π3(k ∈Z )时，上式等号成立. 从而，f (x )的最大值是3√34. 因此，f (x )的值域是[0,3√34]. 故答案为：[0,3√34] 4.3【解析】4. 根据题意得1n[n +n (n−1)2×2]=2011.解得n=2011.于是，该数列所有项的和为20112.设从数列中删去第k 项后剩余项的算术平均值为整数，即20112−(2k−1)2010∈Z .注意到20112=2010×2012+1.则上式等价于2010|2(1−k ) ⇒1005|(1−k ) .因为1≤k ≤2011，所以，k 的取值集合为{1,1006,2011}.故答案为：3 5.2ba【解析】5.由对称性，知点E 在x 轴上.则点E (d,0). 设l BD ：x=kx +d .由{x =kx +d,x 2a 2+y 2b2=1, 消去x 得 (a 2+b2k 2)y 2+2dkb 2y +b 2(d 2−a 2)=0. ①设B (x 1,y 1)、D (x 2,y 2).则y 1、y 2是方程①的根，且y 1<0<y 2.由韦达定理得y 1+y 2=−2dkb2a 2+b 2k2.则m −n=−2y 1−2y 2=−2(y 1+y 2)=4dkb 2a 2+b 2k 2.故m−n d=4kb2a 2+k 2b2≤4kb 22kab=2b a. 当且仅当a 2k=b 2k ，即k =a b时，上式等号成立.故答案为：2b a6.12【解析】6.记事件“第n 次射击命中”为A n ，其概率为P (A n ).则P (A 1)=14.又第n 次射击时距离靶100+50(n −1)=50(n −1)(m )，则P (A n )=(2n+1)2P (A 1)=1(n+1)2.于是，前n 次内命中的概率为P n =1−P (A 1⋅A 2⋅⋅⋅⋅⋅A n )=1−P (A 1)P (A 2)⋅⋅⋅P (A n )=1−(1−1)(1−1)⋅⋅⋅[1−1()2]=1−1⋅3⋅2⋅4⋅⋅⋅⋅⋅n ⋅n +2=1−12⋅n+2n+1=n2(n+1).令n→∞，得lim n→∞P n =12.因此，此人能够命中的概率是12. 故答案为：12 7.11【解析】7.注意到翻折后，三个四点组(A,B,A 1,B 1)、(B,C,B 1,C 1)、(C,A,C 1,A 1)均四点共面，因此，这六个点共可确定平面C 63−3(C 43−1)=11（个）. 故答案为：11 8.22011【解析】8.显然，对任意的非负整数n 均有|z n |=1. 设z n=e iθn (θo ∈[0,2π)).则e iθn+1=e i (π2+θn )e −iθn⇒θn+1=2θn +π2⇒θn+1+π2=2(θn +π2)=⋅⋅⋅=2n (θ0+π2).由z 2011=1，得θ2011=2kπ(k ∈Z )，即22011(θ0+π2)=2kπ+π2. 由θ0∈[0,2π)，得22010π≤2kπ+π2<22010×5π ⇒22011−14≤k <5×22011−14⇒22009≤k <5×22009.因此，满足条件的z n 共有5×22009−22009=22011（个）.故答案为：220119.a =12【解析】9. 设函数f (x )=x 2−2ax −2alnx .则f ′(x )=2x −2a −2ax=2x(x 2−ax −a ). 令f ′(x )=0，即x 2−ax −a =0. 解得x 1=a−√a 2+4a2<0（舍去），x 2=a+√a 2+4a2.当x∈(0,x 2)时，f ′(x )<0，f (x )单调递减；当x ∈(x 2,+∞)时，f ′(x )>0，f (x )单调递增. 故f (x )在x=x 2时取到最小值f (x 2).由f (x )=0有唯一解知f (x 2)=0，即{x 22−2ax 2−2alnx 2=0,x 22−ax 2−a =0..于是，2alnx 2+ax 2−a =0.由a >0，知2lnx 2+x 2−1=0.当x>0时，函数g (x )=2lnx +x −1严格递增，又g (1)=0，从而，x 2=1.由此可解得a =12.10.67【解析】10. 根据题意知a n =1.0·02·=1+2n 3+2n 6+⋅⋅⋅=1+2n 31−1n 3=1+1n 31−1n3=n 3+1n 3−1=n +1n −1⋅n 2−n +1n 2+n +1注意到n 2−n +1=(n −1)2+(n −1)+1.则a 3a 4⋅⋅⋅a n=∏[k+1k−1⋅(k−1)2+(k−1)+1k 2+k+1]n k=3=n (n+1)2×3⋅22+2+1n 2+n+1=76⋅n (n+1)n (n+1)+1.故1a 3a 4⋅⋅⋅a n=67[1+1n (n+1)]=67(1+1n −1n−1). 于是，有lim n→∞1n (1a 3+1a 3a 4+⋅⋅⋅+1a 3a 4⋅⋅⋅a n )=lim n→∞1n ⋅67∑(1+1k −1k+1)n k=3=lim n→∞67⋅1n[(n −2)+13−1n−1]=67.11.（1）见解析；（2）2n【解析】11. 设椭圆G :x 2a 2+y 2b2=1(a >b >0)，直线l ：Ax +By +C =0，P i (x i ,y i )(i =1,2,⋅⋅⋅,n ).则点P i 关于椭圆G 的切点弦l i 的方程为x i xa 2+y i y b2=1 ①（1）直线l j ：x j x a 2+y j y b2=1，由点P i (x i ,y i )在l j 上知x j x ia 2+y j y i b2=1.从而，点P j (x j ,y j )也满足方程①，即点P j 也在直线l i 上. （2）当B=0时，直线l ：x =−CA，即x i =−CA(i =1,2,⋅⋅⋅,n ). ② 由直线l 在椭圆G 外知|−CA |>a . 将式②代入式①整理得y i y b2−(1+CAa 2x )=0.从而，直线l i 恒过定点(−Aa 2C ,0).而|−Aa 2C |<a ，故该定点在椭圆G 内.当B ≠0时，直线l ：y =−A Bx −CB，即y i =−A B x i −CB(i =1,2,⋅⋅⋅,n ). ③ 联立椭圆G 与直线l 的方程并化简得(B2b 2+A 2a 2)x 2+2ACa 2x +a 2(C 2−B 2b 2)=0.由直线l 在椭圆G 外知Δ=4A 2C 2a 4−4(B 2b 2+A 2a 2)a 2(C 2−B 2b 2)=4B 2a 2b 2(B 2b 2+A 2a 2−C 2)<0 =A 2a 2+B 2b 2<C 2.将式③代入式①整理得x i (x a 2−Ay Bb 2)−(Cy 2Bb2+1)=0.此时，直线l i 恒过定点(−Aa 2C ,−Bb2C ). 而1a 2(−Aa 2C )2+1b2(−Bb 2C )2=A 2a 2+B 2b2C 2<1，故该定点在椭圆G 内.综上，直线l i (i =1,2,⋅⋅⋅,n )交于椭圆G 内一定点(−Aa 2C ,−Bb2C).故这n 条直线将椭圆G 分成2n 个区域. 12.见解析【解析】12.如图，联结AD 、BD 、CD 、DE .易知，E 是边BC 的中点，DE ⊥BC .过D 点作DF⊥AB ，DG ⊥AC ，垂足分别为F 、G .由西姆松定理知F 、E 、G 三点共线. 由D 是弧BC ⃑⃑⃑⃑⃑⃑⃑ 的中点，知AD 平分∠BAC . 于是，RtΔADF ≌RtΔADG .从而，DF =DG ，AF =AG .又BC=CD ，结合DF =DG ，得RtΔBDF ≌ RtΔCDG .于是，BF =CG .则AB+AC =(AF +BF )+(AG −CG )=AF +AG =2AF . ①记AD 与FG 的交点为M .则∠DME =90°，即点M 在圆Γ1上. 由圆幂定理得AP 2=AM ⋅AD .而在RtΔADF 中，由射影定理得AF 2=AM ⋅AD .因此，AP=AF .代人式①即得AB+AC =2AP .13.见解析【解析】13. 不妨设x+y +z =4.则xyz =2.故只需寻找x 4+y 4+z 444的最值.此时，有x 4+y 4+z 4=(x 4+y 4+z 4)2−2(x 2y 2+y 2z 2+z 2x 2)=[16−2(xy +yz +zx )]2−2(xy +yz +zx )2+4xyz (x +y +z )=2a 2−64a +288，其中，a =xy +yz +zx .由y +z=4−x 和yz =2x ，知(4−x )2≥8x.解得3−√5≤x ≤2. 类似地，y 、z∈[3−√5,2].这表明，(x −2)(y −2)(z −2)≤0，且(x −3+√5)(y −3+√5)(z −3+√5)≥0. 由此解得a ∈[5,5√5−12].而x 4+y 4+z 444=(a−16)2−112128，故f (x,y,z )=x 4+y 4+z 4(x+y+z )4的最小值和最大值分别为383−165√5256和9128，且分别当(x,y,z )=(3−√5,1+√52,1+√52)和(2,1,1)时取得. 14.见解析【解析】14.任取一个奇质数p ，令(a,b,c,d )=(p −1,p −1,p −2,(p −2)+p 22011).首先证明：这组数满足题中条件.显然，满足条件（1）、（2）.下面证明：这组数满足条件（3）.由a=b=p−1，知(an+b)|(cn+d)⇔a(n+1)|(cn+d).则(n+1)|(cn+d).由cn+d=c(n+1)+(d−c)，知(n+1)|(cn+d)⇔(n+1)|(d−c)，即(n+1)|p22011.从而，n+1∈{p1,p2,⋅⋅⋅,p22011}，n可取p k−1(k=1,2,⋅⋅⋅,22011)，共22011个可能的数.其次证明：这22011个数都符合条件.当n=p k−1(k=1,2,⋅⋅⋅,22011)时，d−cn+1=p22011p k=p22011−k≡1(mod(p−1)).又c≡−1(mod(p−1))，由a=p−1，知a|(c+d−cn+1).又(a,n+1)=1，则(an+b)|(cn+d).因此，满足条件（3）.故(a,b,c,d)=(p−1,p−1,p−2,(p−2)+p22011)（p为任意奇质数）是满足条件的无穷多组正整数.15.19【解析】15.n的最小值为19.当n=18时，表1所示的答题情形不符合要求.表1【注】表l 中（1）、（2）、（3）、（4）为图案，1218为员工，、、分别表示红、黄、蓝三种颜色. 下面证明：当n≥19时，必存在两个人满足要求.事实上，把所有人的文化衫的颜色和图案如上制成表格，若存在两个人的某两种图案的4件文化衫的颜色全部相同，则必存在一个矩形子表，这个子表四个角的方格中的字母（颜色）相同.若对于某个颜色（以红色为例），设A i 分到x i 件红色文化衫.则当∑C x i 2n i=1>6时（约定当x i<2时，C x i 2=0），必存在四个角都是A 的矩形.这是因为，考虑每一列两个A 构成的“对子”，一共只有如表2所示的6种.当∑C x i 2n i=1>6时，必有两列会出现相同的对子，从而，必有四个角都是A 的矩形. 表2当时，任取其中19个人，他们的所有文化衫的颜色中，至少有一种颜色出现了不少于[4×19−13]+1=26（次），不妨设为红色.设其中A i (i =1,2,⋅⋅⋅,19)分到x i （x i 为非负整数）件红色文化衫.则∑x i 19i=1≥26.由调整法易知，当∑C x i 219i=1取最小值时，对任意1≤j <k ≤19，有|x j −x k |≤1.注意到26=1×19+7，则在x i (1≤i ≤19)中有19个1和7个2时，∑C x i 219i=1取得最小值7C 22=7>6.这表明，当n≥19时，必存在四个角都是同一个字母的矩形子表.综上，所求n 的最小值为19.。

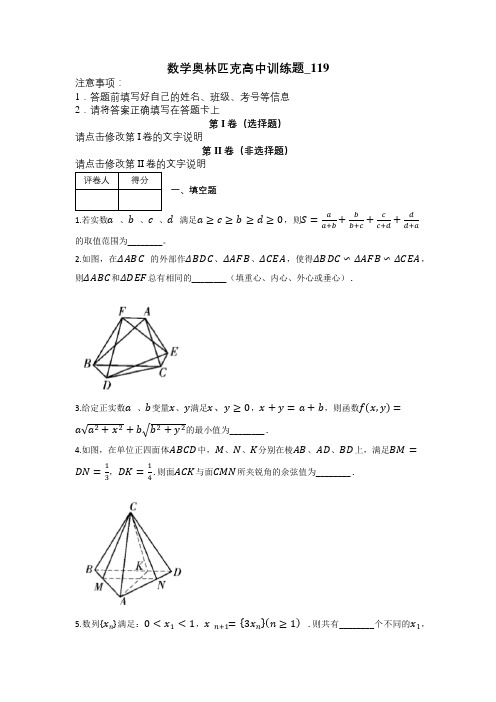
数学奥林匹克高中训练题_119 注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上第I卷（选择题）请点击修改第I卷的文字说明第II卷（非选择题）一、填空题1.若实数a、b、c、d满足a≥c≥b≥d≥0，则S=aa+b+bb+c+cc+d+dd+a的取值范围为________。

2.如图，在ΔABC的外部作ΔBDC、ΔAFB、ΔCEA，使得ΔBDC∽ΔAFB∽ΔCEA，则ΔABC和ΔDEF总有相同的________（填重心、内心、外心或垂心）.3.给定正实数a、b变量x、y满足x、y≥0，x+y=a+b，则函数f(x,y)=a√a2+x2+b√b2+y2的最小值为________.4.如图，在单位正四面体ABCD中，M、N、K分别在棱AB、AD、BD上，满足BM=DN=13，DK=14.则面ACK与面CMN所夹锐角的余弦值为________.5.数列{x n}满足：0<x1<1，x=n+1{3x n}(n≥1) .则共有________个不同的x1，使得{x n }从第一项开始是最小正周期为9的周期数列（{x }=x −[x ]，[x ]表示不超过实数x 的最大整数）. 6.在ΔABC 中，已知AC=1，BC =3√2，以AB 为斜边向ΔABC 外作等腰RtΔABD 则AB +2√2CD 的最大值是________.7.图是一个3×4的方格（其中心的方格线已被划去）.一只青蛙停在A 格处，从某一时刻起，青蛙每隔一秒钟就跳到与它所在方格有公共边的另一方格内，直至跳到B 格才停下..若青蛙经过每一个方格不超过一次，则青蛙的跳法总数为________.8.设AB 是抛物线y 2=2px 的一条焦点弦，且AB 与x 轴不垂直，P 是y 轴上异于O 的一点，满足O 、P 、A 、B 四点共圆，点A 、B 、P 的纵坐标分别为y 1、y 2、y 0.则y 1+y 2y 0的值为________.二、解答题9.实数x 、y i (i=1,2,3) 满足∑x 13i=1=∑y i 3i=1=∑y ix 13i=1=1，试求∑y ix 12+x 1x 2x 33i=1的值.10.若ΔABC 的三边所在直线均与抛物线y 2=2px (p >0)相切，证明：ΔABC 的外接圆必过某个定点，并求出定点的坐标. 11.数列{f n }(n ≥1)的通项为f n=∑C n−2k k [n3]k=0，a n 是f n 除以10以后的余数.试问{a n }是否为周期数列？如果是，请求出{a n }的最小正周期；如果不是，请说明理由. 12.求在图所示的2×6的方格中“圈”的个数.在这里，一条封闭的折线叫做圈，如果这条折线的边均由方格的边组成，且折线经过的任意一个方格顶点都只与折线的两条边相连.13.如图，在四边形ABCD 中，对角线AC 、BD 交于点O .过O 作直线H 1H 2和H 3H4，其中，H 1、H 3在线段AD 上，H 2、H 4在线段BC 上.设直线H 1H 4交线段AB 的延长线于T ，直线H 2H 3交线段CD 的延长线于S .证明：S 、Q 、T 三点共线.14.n 是大于1的整数，正实数a i (i =1,2,⋯,n ) 满足∑a i=1ni=1 .令a n+1=a 1.求证：（1）∑1−a 1a i+1ni=1≥(n −1)2∑a i1−a i+1ni=1； （2）∑a 11+a 1−a i+1≤n−1n ∑a i 1−a i n i=1n i=1； 15.试求出所有的正整数组(m,n,p )(p ≥2)，使得(pmn −1)|(m 2+n 2).参考答案1.[2，52)【解析】1. 因为a ≥c >0，所以，f (x )=x (a−c )(x+a )(x+c )=a−cx+acx+(a+c )在(0，√ac ]上是不减函数.故S=2+[a a+b−c c+b]+[c c+d−a a+d]=2+b (a−c )(b+a )(b+c)−d (a−c )(d+a )(d+c )=2+f (b )−f (d )≥2又a≥c ≥b >0，则S =1+[a a+b+b b+c]−[d c+d−d a+d]≤1+a a+b+b b+c<1+a+b a+b+b 2b=52.取a=b =c =d =1，则S =2；取a →+∞，b =c =1，d →0，则S →52.综上，S∈[2,52).2.重心【解析】2.建立复平面，设点A 在复平面内对应的复数为A ，其余类似. 由ΔBDC ∽ ΔAFB ∽ ΔCEA ，可设∠DBC=∠ECA =∠FAB =θ，|BD ||BC |=|CE||CA |=|AF ||AB |=k .令ke −iθ=z .则D−B C−B=|BD ||BC |e −i∠DBC=z ，即D −B =z (C −B ). 同理，E −C =z (A −C )，F −A =z (B −A )..将上述三式相加得A +B +C =D +E +F .这表明，ΔABC 和ΔDEF 总有相同的重心.3.(a +b )√a 2+b 2【解析】3.由柯西不等式得√a 2+x 2⋅√a 2+b2≥a 2+bx ，√b 2+y 2⋅√b 2+a 2≥b 2+ay . 则f (x,y )=2+x 2+b√b 2+y 2≥2√a 22+b 2√a 22=23√a 22=(a +b )√a 2+b 2.当且仅当x =b,y =a 时，上式等号成立.4.√69【解析】4.如图，记MN 与AK 交于点G ，并设面ACK 与面CMN 所成的锐角大小为θ. 作CO⊥面ABD 于点O .延长AO 交BD 于点X .易知O 是ΔABD 的中心.则AO =2OX ，BX =XD .又AM=2MB ，AN =2ND ，因此，M 、O 、N 三点共线，O 是MN 的中点.由AC ⊥MN ，AC ⊥CO 知AC ⊥面CMN .故ΔACG 在面CMN 上的投影为ΔOCG .由面积射影定理得cosθ=S ΔCOG S ΔACG=14SΔCMN 23SΔACK=14×√6923×12×34=√695.19656【解析】5. 不妨令0≤x 1≤1.若x 1=0或1，则当n ≥2时，x n =0.这样的数列不满足题意.设x 1在三进制下可表示为(0.a 1a 2⋯)3，a 1∈{0,1,2}.则{x n }是周期为T 的周期数列⇔{a n }是周期为T 的周期数列⇔ x 1在三进制下是循环小数，且循环节长为T . 因此，使{x n }是以T 为周期的周期数列x 1共有3个.设所有最小正周期为9的数列{x n }组成集合A ，所有周期为9的数列{x n }组成集合B ，所有周期为3的数列{x n }组成集合C ，则A ∩C =∅，A ∪C =B .从而，最小正周期为9的数列{x n }共有|A |=|B |−|C |=39−33=19656 个，这些数列所对应x 1也有19656个.6.10【解析】6.如图，以BC为直角边、C为直角顶点向外作等腰RtΔBCE，联结AE，设∠ACB=θ.由AB=√2BD，BE=√2BC，∠EBA=∠CBD，知ΔEBA∽ΔCBD.则AECB =BEBC=√2在ΔACE中，AE=√AC2+BC2−2AC⋅BC[cosθ+π2]=√19+6√2sinθ在ΔABC中，AB=√AC2+BC2−2AC⋅BCcosθ=√19-6√2cosθ故AB+√2CD=√19+6√2sinθ+√19−6√2cosθ≤√2(19+6√2sinθ+19−6√2cosθ)=√76+24[sinθ−π4]≤√100=10.当且仅当θ=3π4时，上式等号成立.7.26【解析】7.如图，分两种情况讨论.（1）如果青蛙不经过M格，则有2条路径：APCDRB，AQSEFB.（2）如果青蛙经过M格，若某时刻青蛙跳到C格，则它下一秒内一定跳至D格；若某时刻青蛙跳到D 格，则它下一秒内一定不会跳至C 格.因此，可将C 、D 两格合并为一个大方格（设之为G ）.同样地，可将E 、F 两格合并为大方格H . 如果两个方格有公共边，则在两个方格间连上虚线，如图9.由图可知，P 、G 、R 和Q 、S 、H 对称地分布在直线AB 的两侧.显然，青蛙第一步必跳入P 、Q 两格中的某格，倒数第二步必跳入R 、H 两格中的某格. 如果青蛙第一步跳至P 格，倒数第二步跳至R 格，那么，这样的路径有3条：APGMRB ，APMPB ，APMGRB .如果青蛙第一步跳至Q 格，倒数第二步跳至R 格，设青蛙第k 秒钟跳至M 格，第k −1秒跳至X 格，第k+1 秒跳至Y 格.则X 格可以是Q 、S 、H 、Y 格可以是P 、G 、R .因此，这样的路径有3×3=9条. 由对称性知，如果青蛙第一步跳至Q 格，倒数第二步跳至H 格，则这样的路径有3条；如果青蛙第一步跳P 格，倒数第二步跳至H 格，则这样的路径有9条. 综上，青蛙的跳法总数为2(9+3)+2=26. 8.4【解析】8.如图，设直线1AB :ky =x −p2，与抛物线方程联立得y 2−2pky −p 2=0.由于y 1、y 2是方程的两根，且y 1≠y 2，则由韦达定理得y 1y =2−p 2.设直线PA 、PB 的斜率分别为k 1、k 2.则k 1=y 1−y 0y 122p=2p (y 1−y 0)12，k 2=2p (y 2−y 0)22. 因为A 、P 、O 、B 四点共圆，所以，∠APB=∠AOB ，tan∠APB =tan∠AOB .而 tan∠APB =k 1−k 21+k 1k 2=2p (y 1−y 0)y 12−2p (y 2−y 0)y 221+2p (y 1−y 0)y 12⋅2p(y 2−y 02)y 22=2p (y 2−y 1)[y 1y 2−y 0(y 1+y 2)]p 4+4p 2(y 1−y 0)(y 2−y 0).令y 0=0，可得tan∠APB =2p (y 2−y 1)y 1y 2p 4+4p 2y 1y 2=2(y 2−y 1)3p.故tan∠APB =tan∠AOB ⇔2p (y 2−y 1)[y 1y 2−y 0(y 1+y 2)]p +4p (y 1−y 0)(y 2−y 0)=2(y 2−y 1)3p.又y 1−y 2≠0，则tan∠APB =tan∠AOB ⇔y 1y 2−y 0(y 1+y 2)p 2+4(y 1−y 0)(y 2−y 0)=13⇔3y 1y 2−3y 0(y 1+y 2)=p 2+4(y 1−y 0)(y 2−y 0).将−p 2=y 1y 2代入上式得y 0(y 1+y 2)=4y 02.由于y 0≠0，故y 1+y 2y 0=4.9.0【解析】9. 令a i =y i x 1(i =1,2,3).于时，∑a i =∑a i x 1=13i=13i=1.故y 1x 12+x 1x 2x 3=y 1x 1x 1(x 1+x 2+x 3)+x 2x 3=a 1(x 1+x 2)(x 1+x 3)=a 1−a 1x 1(x1+x 2)(x 2+x 3)(x 3+x 1).同理，y 2x 22+x 1x 2x 3=a 2−a 2x 2(x1+x 2)(x 2+x 3)(x 3+x 1)，y 3x 32+x 1x 2x 3=a 3−a 3x 3(x1+x 2)(x 2+x 3)(x 3+x 1).则∑y ix 12+x 1x 2x 3=∑a 1−∑a 1x 13i=13i=1(x1+x 2)(x 2+x 3)(x 3+x 1)=03i=1.10.见解析【解析】10.如图，不妨设点A 和抛物线在直线BC 的两侧，且点B 在C 的上方.并设直线AB 、BC 、CA与抛物线的切点分别为D 、E 、F 设D(y 122p ,y 1)、E(y 222p ,y 2)、F(y 322p ,y 3)、S(p 2,0).易求得k AB =py 1，k AC =py 3.则1AB :y −y 1=p y 1[x −y 122p ]， 即y 1y =px +y 122p ，1AC :y 3y=px +y 322p .联立两方程得A(y 1y 32p,y 1+y 32).同理，B(y 1y 22p,y 1+y 22)、C(y 2y 32p,y 2+y 32).故tan∠BAC=k AB −k AC 1+k AB k AC=p y 1−py 31+p 2y 1y 3=p (y 3−y 1)p 2+y 1y 3，于是，k BS=y 1+y 22y 1y 22p −p2=p (y 1+y 2)y 1y 2−p 2，k CS=p (y 3+y 2)y 3y 2−p 2.则tan∠CSB=p (y 1−y 3)p 2+y 1y 3=−tan∠BAC .因此，∠BAC+∠BSC =π.所以ΔABC 的外接圆恒过点S(p2,0).显然，ΔABC 的外接圆不可能同时通过两个不同的定点. 因此，(p2,0)是外接圆通过的唯一定点.11.见解析【解析】11.{a n }是周期数列，最小正周期为217. 易知f 1=f 2=1，f 3=2，f 4=3，f 5=4.下面证明：当n ≥4时，f n+2=f n+1+f n−1. ①（1）当n≡0或2(mod3)时，[n+23]=[n+13].则f =n+2∑C n+2−2k k [n+23]k=0=C n+10+∑C n+2−2k k−1[n+23]k=1+∑C n+1−2k k[n+23]k=1=∑C n−1−2kk[n−13]k≡0+∑C n+1−2k k[n+13]k≡0=f n+1+f n−1.（2）当n ≡1(mod3)时， 令r=n−13∈Z .则f n+2=∑C n+2−2kk =2+r+1k=0∑C n+2−2k k r k=1=∑C n−1−2(k−1)k−1+∑C n+1−2k krk=1rk=1+2=[∑C n−1−2k k +C n−1−2r rr−1k=0]+[∑C n+1−2k k +C n+10rk=1]=∑C n−1−2k k +∑C n+1−2k k[n+13]k=0[n−13]k=0=f n+1+f n−1设u k 是f k 除以2所得的余数，v k 是f k 除以5所得的余数.由式①可得{u k }的各项为：1,1,0,1,2,2,1,1,1,0,1,0,0,1,⋯ {v k }的各项为：1,1,2,3,4,1,4,3,4,3,1,0,3,4,4,2,1,0,2,3,3,0,3,1,1,4,0,1,0,0,1,1,1,2,3⋯由上可知，{u k }是最小正周期为7的周期数列；{v k }是最小正周期为31的周期数列. 它们的循环节分别如划线部分所示.又(2,5)=1，故f k 除以10所得余数是周期数列，最小正周期是7和31的最小公倍数，即217. 12.681【解析】12.定义某个圈在方格水平方向的投影长为这个圈的“圈长”. 首先求2×k 的方格（如图）中圈长为k 的圈的个数a k .这些圈中都至少包含了A 、B 格中的一个，设其中包含A 格但不包含B 格的有x k 个， 包含B 格但不包含A 格的有y k 个，包含A 、B 两格的有z k 个.因此，a k =x k +y k +z k .由对称性知x k=y k ，又包含A 、B 格的圈，必须至少包含C 、D 格中的一个，故z k =a k−1；包含A 格但不包含B 格的圈必包含C 格，故x k =x k−1+z k−1.由以上四式得a k =2a k−1+a k−2.下面计算a 1、a 2.如图（a ）,在2×1的方格中圈长为1的圈共有3个：ABDCA ，CDFEC ，ABDFECA .（a ） （b ）如图（b ），在2×2的方格中圈长为2的圈共有7个：GHILKJG ，JKLONMJ ，GHILONMJG ，GHILONKJG ，GHILKNMJG ，HILONMJKH ，GHKLONMJG .所以，a 1=3，a 2=7因此，a 3=17，a 4=41，a 5=99，a 6=239.故2×6棋盘中圈的个数为∑(7−i )a i =68161=1.13.见解析【解析】13. 先证明一个引理.引理 如图在四边形ABCD 中，对角线AC 、BD 交千点O 、P 、Q 分别是线段AB 、CD 外的点.如果P 、O 、Q 三点共线，则CQ QD ⋅DO OB ⋅BP PA ⋅AOOC =1.引理的证明：由于P 、O 、Q 三点共线，则∠AOP=∠COQ ，∠BOP =∠DOQ ，故CQ QD ⋅BPPA =SΔOCQ S ΔOQD⋅S ΔOBPS ΔOPA=SΔOCQ S ΔOAP⋅S ΔOBP S ΔOQD=OB⋅OP OD⋅OQ ⋅OC⋅OQ OA⋅OP =OC OA ⋅OB OD .因此，CQ QD ⋅DO OB ⋅BP PA⋅AO OC=1.回到原题. 分两种情况讨论.（1）如图，当AD 与BC 不平行时，设AD 与BC 交于点M .对ΔMAC 与截线H 1OH 2，有MH 1H 1A ⋅AO OC ⋅CH2H 2M =1；①对ΔMBD 与截线H 3OH 4，有H 3M DH 3⋅MH 4H 4B ⋅BOOD=1；②对MCD 与截线H 2H 3S ，有MH 2H 2C ⋅CS SD ⋅DH 3H 3M=1； ③ 对ΔMBA 与截线H 1H 4T ，有H 4M BH4⋅MH 1H 1A ⋅ATTB=1； ④ ①÷②×③÷④得CS SD ⋅DO OB ⋅BT TA ⋅AOOC=1.故BTTA=BT ′T ′A.因此，点T 与T ′重合.所以，S 、O 、T 三点共线. （2）当AD ∥BC 时，有CS SD =CH 2DH 3，DO OB =DH 3BH 4，BT TA =BH 4AH 1，AOOC =AH 1CH 2.①÷②×③÷④得CS SD ⋅DO OB ⋅BT TA ⋅AO OC=1.设射线SO 交线段AB 的延长线于点T ″.理可以证明点T 与T ′重合. 所以，S 、O 、T 三点共线. 14.（1）见解析；（2）见解析【解析】14. （1)令a 0=a n ，对任意的i (i =1,2,⋯,n )，由均值不等式得a 11−ai+1=a i∑a j1≤j≤n,j≠i+1≤i(n−1)n−1√∏a j1≤j≤n,j≠i+1=1n−1√∏a ia j1≤j≤n,j≠i+1n−1≤1(n−1)2∑a ia j1≤j≤n,j≠i+1.故∑a i 1−a i+1≤1(n−1)2∑∑a i a j=1(n−1)2[∑a i ∑1a i−ni=1ni=11≤j≤nj≠i+1n−1i=0n i=1∑a ia i+1ni=1]=1(n−1)2∑1−a i a i+1n i=1. 因此，∑1−a i a i+1≥(n −1)2∑a i1−a i+1ni=1ni=1.当且仅当a i=1n(i =1,2,⋯,n )时，上式等号成立.（2）设i 1,i 2,⋯,i n 是1,2,⋯,n 的一个排列，满足a i 1≥a i 2≥⋯≥a i n .因此11−ai 1≥11−a i 2≥⋯≥11−a i n.由排序不等式得∑a i 1−a i=∑a ij 1−a ij≥∑a i1−a i+1ni=1nj=1ni=1.①由柯西不等式得∑a i 1−a i≥[∑n i=1a ]2∑a 1−∑a 12ni=1ni=1≥[∑n i=1a ]2∑a 1n i=1−1n [∑ni=1a ]2=n n−1ni=1.②对任意的i (i=1,2,⋯,n )，由均值不等式得ai1+a i−ai+1=a ia i +(n−1)⋅1−ai+1n−1≤in √a i(1−ai+1)n−1(n−1)n−1=n−1n √1n−1[a i 1−a i+1]n−1n≤n−1n[(n −1)⋅a i 1−a i+1+1n−1].③由式①、②、③得∑a i1+a i −a i+1≤(n−1)2n 2ni=1∑a i 1−a i+1+1n ≤ni=1(n−1)2n 2∑a i 1−a i +n−1n 2∑a i1−a i=n−1n∑a i1−a in i=1ni=1ni=1. 当且仅当a i =1n(i =1,2,⋯,n )时，上式等号成立. 15.见解析【解析】15. 由题意设m 2+n 2=k (pmn −1)(k ∈N +).①下面分两种情况讨论. （1）若m =n ，则k =2m 2pm −1≥1.因此，(p −2)m 2≤1.显然，p ≤3.若p=3，则m 2≤1，故只能有m =n =1；若p =2，则k =2m 22m −1=1+12m −1是正整数，故只可能有m=n=1.（2）若m≠n，由对称性不妨假设m>n，即m≥n+1.考虑二次方程x2−pknx+(n2+k)=0，②其中，m是方程②的一个根.设方程的另一根为y.由韦达定理有是m+y=pk，my=n2+k>0.所以，y为正整数且y=pkn−m.下面证明：当n≥2时，y>n.事实上，n−y=m+n−pkn=m+n−pn⋅m2+n2 pmn−1=(pmn−1)(m+1)−pn(m2+n2)pmn−1=pmn2−pn3−m−npmn−1.又p≥2，m≥n+1，则pmn2−pn2−m−n≥2mn2−2n3−m−n= m(2n2−1)−(2n3+n)≥(n+1)(2n2−1)−(2n3+n)=2n(n−1)−1≥3≥0.所以，n−y>0，y<n成立.由于m和y=pkn−m是方程②的两个根，因此，对某个p，如果一组(m,n)=(m0,n0)(m0>n0>1)是方程①的解，那么，(m′,n′)=(n0,pkn0−m0)也是方程①的解.而m0>n0=m′>n′，可因此，对方程①的任意一个解(m,n)(m>n>1)，用(n,pkn−m)来替换原来的(m,n)，式①仍然成立.只要这里的n>1，这样的替换便可以继续下去.而每经过一次这样的替换，n的值将会减少.因此，经过有限步之后，必有n=1.下面讨论n=1时，方程①的解.（i）若k=1，则方程①即为m2−pm+2=0.而m>1，故仅有解(m,n,p)=(2,1,3).此时，k=1.（ii）若k≥2,则有m2+1≥2(pm−1).③因为k=m2+1pm−1是正整数，所以，p2k=p2m2+p2pm−1=pm+1+p2+1pm−1是正整数.故(pm−1)|(p2+1).如果m≥p+1,则p2+1≥pm−1≥p2+(p−1).解得p≤2.于是，p=2,m=p+1=3,即(m,n,p)=(3,1,2),此时，k=2.如果m≤p,代入式③可得m2+1≥2(m2−1),即m≤√3与m≥2矛盾.因此，p只能取2,3.当p=2时，方程①的任意一个解(m,n)(m>n>1)经过有限次替换以后必将变为(3,1).反过来，对(3,1)作上述替换的逆变换(m,n)→(4m−n,m)，a1)(i=1,2,⋯)，将生成方程的全部解.这些解可表示为(a,i+1在这里，数列{a n}满足a=11，a2=3以及递推关系a i+1=4a i−a i−1.同理，当p=3时，方程的全部解为(b i+1,b i)(i=1,2,⋯)，在这里，数列{b n}满足b1=1,b2=2以及递推关系b i+1=3b1−b i−1.当m<n时，由对称性可知，方程的全部解为(m,n,p)=(a i,a i+1,2)以及(b,b i+1,3)(i=1,2,⋯).因此，全部解为(m,n,p)=(a i+1,a,2),(a,a i+1,2),(b i+1,b i,3),(b,b i+1,3)(i=1,2,⋯).其中，数列{a n}满足a=1a2=1，a i+1=4a1−a i−1；数列{b n}满足b1= b2=1，b i+1=3b1−b i−1.。

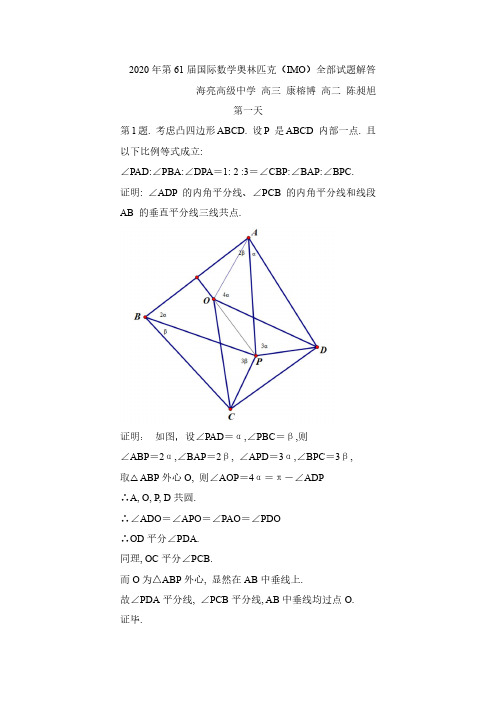
2020年第61届国际数学奥林匹克（IMO）全部试题解答海亮高级中学高三康榕博高二陈昶旭第一天第1题. 考虑凸四边形ABCD. 设P 是ABCD 内部一点. 且以下比例等式成立:∠PAD:∠PBA:∠DPA＝1: 2 :3＝∠CBP:∠BAP:∠BPC.证明: ∠ADP 的内角平分线、∠PCB 的内角平分线和线段AB 的垂直平分线三线共点.证明：如图，设∠PAD＝α,∠PBC＝β,则∠ABP＝2α,∠BAP＝2β, ∠APD＝3α,∠BPC＝3β,取△ABP外心O, 则∠AOP＝4α＝π－∠ADP∴A, O, P, D共圆.∴∠ADO＝∠APO＝∠PAO＝∠PDO∴OD平分∠PDA.同理, OC平分∠PCB.而O为△ABP外心, 显然在AB中垂线上.故∠PDA平分线, ∠PCB平分线, AB中垂线均过点O.证毕.第2题. 设实数a, b, c, d 满足a ≥b ≥c ≥d > 0, 且 a + b + c + d = 1. 证明:(234)1a b c d a b c d a b c d +++<. 证明: 由加权AM －GM 不等式, 我们有2222a b c d a b c d a a b b c c d d a b c d <⋅+⋅+⋅+⋅=+++ 故只需证明22223(234)()()cyca b c d a b c d a ++++++<∑ (*)注意到332()36cyc cyc sym cyca a ab abc =++∑∑∑∑, 及32222cyca ab ad a a ++≥∑2232222222cyca b ab b bc bd b a ++++≥∑2222233333cyca cbc ac cd c a +++≥∑22234444cyc a d a b abd acd bcd d a ++++≥∑∴ (*)成立. 故原不等式成立.第3题. 有4n 枚小石子, 重量分别为1, 2, 3, . . . , 4n. 每一枚小石子都染了n 种颜色之一, 使得每种颜色的小石子恰有四枚. 证明: 我们可以把这些小石子分成两堆, 同时满足以下两个条件:• 两堆小石子有相同的总重量;• 每一堆恰有每种颜色的小石子各两枚.证明: 引理:将n 种颜色的点个4个两两分组, 则可取n 组使得每种颜色的点各2个.即证: n 阶4-正则图G(不一定简单)必有2-正则生成子图. n ＝1, G 为v 的2个自环, 成立.设0n n ≤成立, 则01n n =+时:若G 有点含两自环或有两点含4重边, 对其余部分用归纳假设,该部分取1自环或2重边即可.下设无这样的结构.若G 含三重边,设x,y 间有三条边, 且,(,)xu yv G u y v x ∈≠≠. 考虑将x,y 去掉, 并添入边uv 得到图G ’. 由归纳假设, 图G ’有2-正则生成子图, 若该图含添入的边 uv, 删去该边并加入ux, xy, yv 即可. 若不含, 加入xy, xy 即可.下设无三重边.显然G 有圈. 设最小圈为121,,...,t x x x x . 由G 无2自环,3重边知01t n <+, i x 有两边不指向12,,...t x x x . 设这两边指向,i i u v ，以下下标模t.在G 中删去点12,,...t x x x 并加入边1(1)i i i e u v i t +=≤≤得到G’. 由归纳假设, G ’有2-正则子图G 1.对1≤i ≤t, 若1i e G ∈, 则选择G 中的边11,i i i i x u x v ++, 若1i e G ∉, 则选自1i i x x +, 其余边按G 1中边选择, 则选出的边即为G 的2-正则生成子图的边集.结论成立.回到原题. 将重量为{,41}k n k +-的小石子分为一组.(12)k n ≤≤, 由引理可取n 组使每种颜色的小石子恰2个. 这2n 个分为一组, 其余分为一组, 此即满足条件的分法, 命题成立.第二天第4题. 给定整数n > 1. 在一座山上有n2个高度互不相同的缆车车站. 有两家缆车公司A和B, 各运营k辆缆车; 每辆从一个车站运行到某个更高的车站(中间不停留其他车站). A 公司的k辆缆车的k个起点互不相同，k个终点也互不相同, 并且起点较高的缆车，它的终点也较高. B公司的缆车也满足相同的条件. 我们称两个车站被某个公司连接，如果可以从其中较低的车站通过该公司的一辆或多辆缆车到达较高的车站(中间不允许在车站之间有其他移动). 确定最小的正整数k, 使得一定有两个车站被两个公司同时连接.解: 由题意得, 每个缆车与1或2个缆车相连. (否则有两辆缆车起点不同, 终点相同)∴A, B各自的缆车线路图可划分为若干个链.注意到每条链长度大于等于2, 且首尾两点不能作为终点和起点, 故恰有2n k-条链.若21k n n≥-+, 则A最多由n－1条链.由抽屉原理, 其中至少有一条链上有221nnn⎡⎤=+⎢⎥-⎢⎥个点, 设为P. 而B仅有n－1条链, 故P上一定有两个点同时在B 的一条链上, 则这两点可被两个公司同时连接.另一方面, 2k n n=-时, 记2n个车站高度排序为21,2,...n (从低到高)令A的2n n-辆缆车为2(1)i n i i n n→+≤≤-令B的2n n-辆缆车为21(11,|)i i i n n i→+≤≤-/易见此时任两个车站不能被两个公司同时相连.2 min 1k n n∴=-+.第5题. 有一叠n > 1张卡片. 在每张卡片上写有一个正整数. 这叠卡片具有如下性质：其中任意两张卡片上的数的算术平均值也等于这叠卡片中某一张或几张卡片上的数的几何平均值.确定所有的n, 使得可以推出这叠卡片上的数均相等? 解: 设这n 张卡片上的数为1212,,....(...)n n x x x x x x ≤≤. 若12gcd(,,...)1n x x x d =>, 用i x d 代替i x , 不影响结果. 故不妨设12gcd(,,...)1n x x x =.由题意得, 1,2i jx x i j n +∀≤≤≤为代数整数.则2|i j i x x x +⇒模2同余. 又12gcd(,,...)1n x x x =, 故i x 全为奇数.任取一个素数p, p ≥3.记{|1,|},{|1,|}i i i i A x i n p x B x i n p x =≤≤=≤≤/ 则对,,2x y x A y B +∀∈∈不为p 的倍数. 设121(...)2k k i i i x y x x x +=, 则121|(...)2k k i i i x y p x x x +=/ ∴对1,j i j k x B ∀≤≤∈.max 2i i x B x y x ∈+∴≤. 取max ,max i i i i x A x B x x y x ∈∈==, 则max max i i i i x A x B x x ∈∈≤若1n x ≠, 取n x 的奇素因子p, 由12gcd(,,...)1n x x x =知, i ∃, 使|i p x /.取0max{|1,|}i i i i n p x =≤≤/, 由上述结论知0n i x x ≤, 则o n i x x =. 又0|,|i n p x p x /, 矛盾!1n x ∴=. 则1,1i i n x ∀≤≤=.∴对任意n ≥2, 卡片上的所有数均相等.第6题. 证明: 存在正常数c 具有如下性质:对任意整数n > 1, 以及平面上n 个点的集合S, 若S 中任意两点之间的距离不小于1，则存在一条分离S 的直线ℓ, 使得S 中的每个点到直线ℓ 的距离不小于13cn -.(我们称直线ℓ分离点集S, 如果某条以S 中两点为端点的线段与ℓ 相交.)证明: 以每个点为圆心,12为半径作圆, 则这些圆两两公共部分面积为0.引理1: 对凸多边形P, 其内部最多由421s l π++个点在S 中,其中s,l 代表P 的面积和周长. 证明: 如图, 将P 的每条边往外侧平移12, 并以P 上每个点为圆心, 12为半径作圆, 拓展区域面积为124l π+. ∴P 内部最多1422414S l s l πππ+++=+个点. 现在对于一条直线l, 作S 中每个点在l 上的投影. 任取相邻两个投影点, 则这两点连线的中垂线分离点集S, 且所有的到该直线的距离≥12投影点距离.设S 的直径为D, 则可作一个以D 为边长的正方形覆盖S. 由引理1, 122481()D Dn D n π++≥⇒=Ω 设P,Q ∈S, PQ ＝D. 将PQ 作为上述l, 记我们所能做到的使每个点到一条直线的距离均不小于该数的最大值为d.由于仅与夹角有关, 故d 存在.而l 上除P,Q 外有n －2个投影点.2(1)2D D d n n∴≥>-. 又12()D n =Ω, 故12()d n -=Ω. 需证明13()d n -=Ω .取点集S 的凸包P. 若一直线过P 上一点且使得S 中所有点都在该线一侧, 我们认为其亦分离S. 称其为支撑边. 对于任一常数C, 作两条平行的距离为C 的直线, 满足这两条直线分离S. 作他们的垂线l, 设这个带状区域内有m 个S 中的点, 则11c c d m m d≥⇒≥-+. 不妨设(1)d o =, 则可以认为m 远远大于1. 为使m 尽量小, 应取两直线其中之一为支撑边.∴现在对于一条分离S 的直线l, 设l 与P 围成的区域内部有B 个点. P 中与l 距离最近的点到l 距离为0s , 则01s d B ≥+ (以下用≥代表数量级估计) 我们证明d≥从而311D d n D n ≥⋅= 则13()d n -=Ω. 如图, P 夹在这样一个区域里, 取XY 上一点Z, 使得0YZ s =. 过Z 作MN ⊥XY , 点M,N 在以X 为圆心, D 为半径的圆上. 则B ≤YMN 内S 中点的个数.不妨设XY 为x 轴, 对YMN 内任意两点1122(,),(,)x y x y , 221201212||,()()1x x s x x y y -≤-+-≥, 则12||1y y B -≥⇒≤+.而MN =02s d MN∴≥=+由于0(1)s =Θd ∴≥, 则13d n -≥, 即13()d n -=Ω证毕.。

数学奥林匹克高中训练题（20）第一试一、选择题（本题满分 36分，每小题6分）x — a1.（训练题25）已知函数y 的反函数的图象关于点（-1,3）成中心对称图形，则实数 a 等于x-a -1（A ）.（A ） 2 （B ）3（C ）-2（D ）-4,5 I222.（训练题25）我们把离心率等于黄金比 丄二的椭圆称之为“优美椭圆”.设二•爲=1（a > b >2a 2b 20）为优美椭圆，F, A 分别是它的左焦点和右端点，B 是它的短轴的一个端点，贝y ■ ABF 等于（C ）.复数一定是（C ）.Z 26.（训练题25）在集合M 二｛1,2,3,）11,10｝的所有子集中，有这样一族不同的子集,不是空集，那么这族子集最多有（B ）. （A ） 210 个（B ） 29 个（C ）102 个（D ） 92 个(A) 60o(B)75°(C)90o(D)120°3.（训练题25）已知 ABC 三边的长分别是a,b,c , 复数Z i ,Z 2满足 Z i =a, Z 2 =b,乙+ z 2 = c ，那么（A ）是实数(B)是虚数(C)不是实数(D) 不是纯虚数4.（训练题25）函数 f (X)二 1（-厂卩：21 c2 c 2CE 的最大值是（D ）. (A) 20(B)10(C)-10(D)-205 .（训练题 25）以O 为球心，4为半径的球与三条相互平行的直线分别切于A,B,C 三点.已知S.BOC = 4 ,S ABC 16，则• ABC 等于(B).Ji(A)—12(B)5■： 7■:12(C)12(D)11- 12它们两两的交集都二、填空题（本题满分54分，每小题9分）1.（训练题25）在直角坐标系中，一直角三角形的两条直角边分别平行于两坐标轴，且两直角边上的中3线所在直线方程分别是 v =3x • 1和v = mx • 2，则实数m 的值是3或124x2 •（训练题25）设f （x ） J （a .0,a "） , [m]表示不超过实数m 的最大整数，则函数1+a x1 1[f （x ） ] [f （-x ）]的值域是 ___________ {-1,0} ________ •2 2 ------------------------------3 •（训练题25）设a, b,c 是直角三角形的三条边长，c 为斜边长，那么使不等式a 2 （bc ） b 2 （c a ） c 2 （a • b ） _ kabc 对所有直角三角形都成立的 k 的最大值是2 3 r 2•4.（训练题25）如图，正三棱柱 ABC -ABG 的各条棱长都是1,截面BCD 1 在棱AA 上的交点为D ,设这个截面与底面ABC 和三个侧面ABB 1A 1,BCC 1B 1,CAAC 1所成的二面角依次为：「，：七，〉，若 c o ：s^ c o 2s-c 3o S，则截面的面积等于 —3乜 _______________85.（训练题25）已知f （x ）是定义域在实数集的函数，且f （X • 2）[1 - f （X ）] =1 • f （x ）•若f （1） =2，,3 , 则 f （1949）的值是 ___________ p 3 - 2 .6.（训练题25）设x 1是方程.3sin x 「3cosx = 2a 「1的最大负根，x 2是方程2cos 2x 「2sin 2x = a 的最小正根，那么，使不等式为Ex?成立的实数a 的取值范围是 ________ - -43^a^~或 a= 2 __________.2第二试一、 （训练题25）（本题满分25分）某眼镜车间接到一任务，需要加工 6000个A 型零件和2000个B 型 零件，这个车间有 214名工人，他们每一个人加工 5个A 型零件的时间可加工 3个B 型零件•将这些 人分成两组同时工作，每组加工同一型号的零件，为了在最短的时间完成，应怎样分组？ 77二、 （训练题25）（本题满分25分）已知一个四边形的各边长都是整数， 并且任意一边的长都能整除其余三边之和.求证：这个四边形必有两边相等.B 1B（训练题25）（本题满分35 分）实数数列a1, a2, |a3, ,a M足a P 帕弋钏帕996—為97=1997若数列｛0｝满足：b k = ai+：+川％（k =1,2川1997）.求bf —b2 + b2 —…+0 996-匕997的最大可能值.四、（训练题25）（本题满分35分）给定两个七棱锥，它们有公共的底面A,A2A3A4A5A6A7，顶点R,P2在底面的两侧•现将下述线段中的每一条染红，蓝两色之一：R,P2，底面上的所有的对角线和所有的侧棱.求证：图中心存在一个同色三角形.。

ORQN MFED CBAP2020年中国数学奥林匹克试题与解答(2020年1月11日)一、给定锐角三角形PBC ，PC PB ≠．设A ，D 分别是边PB ，PC 上的点，连接AC ，BD ，相交于点O. 过点O 分别作OE ⊥AB ，OF ⊥CD ，垂足分别为E ，F ，线段BC ，AD 的中点分别为M ，N ．（1）若A ，B ，C ，D 四点共圆，求证：EM FN EN FM ⋅=⋅；（2）若 EM FN EN FM ⋅=⋅，是否一定有A ，B ，C ，D 四点共圆？证明你的结论． 解（1）设Q ，R 分别是OB ，OC 的中点，连接EQ ，MQ ，FR ，MR ，则11,22EQ OB RM MQ OC RF ====，又OQMR 是平行四边形， 所以OQM ORM ∠=∠， 由题设A ，B ，C ，D 四点共圆， 所以ABD ACD ∠=∠，于是22EQO ABD ACD FRO ∠=∠=∠=∠，所以EQM EQO OQM FRO ORM FRM ∠=∠+∠=∠+∠=∠， 故 EQM MRF ∆≅∆， 所以 EM ＝FM ， 同理可得 EN ＝FN ，所以 EM FN EN FM ⋅=⋅． （2）答案是否定的．当AD ∥BC 时，由于B C ∠≠∠，所以A ，B ，C ，D 四点不共圆，但此时仍然有EM FN EN FM ⋅=⋅，证明如下：如图2所示，设S ，Q 分别是OA ，OB 的中点，连接ES ，EQ ，MQ ，NS ，则11,22NS OD EQ OB ==，所以NS ODEQ OB=． ① 又11,22ES OA MQ OC ==，所以ES OAMQ OC=． ② 而AD ∥BC ，所以OA ODOC OB=， ③ 由①，②，③得NS ESEQ MQ=． 因为 2NSE NSA ASE AOD AOE ∠=∠+∠=∠+∠，()(1802)EQM MQO OQE AOE EOB EOB ∠=∠+∠=∠+∠+︒-∠(180)2AOE EOB AOD AOE =∠+︒-∠=∠+∠， 即NSE EQM ∠=∠，所以NSE ∆～EQM ∆，故EN SE OAEM QM OC==（由②）． 同理可得， FN OAFM OC =， 所以 EN FNEM FM=， 从而 EM FN EN FM ⋅=⋅．二、求所有的素数对（p ，q ），使得q p pq 55+．解：若pq |2，不妨设2=p ，则q q 55|22+，故255|+qq ．由Fermat 小定理， 55|-qq ，得30|q ，即5,3,2=q ．易验证素数对)2,2(不合要求，)3,2(，)5,2(合乎要求．若pq 为奇数且pq |5，不妨设5=p ，则qq 55|55+，故6255|1+-q q ．当5=q 时素数对)5,5(合乎要求，当5≠q 时，由Fermat 小定理有15|1--q q ，故626|q ．由于q 为奇素数，而626的奇素因子只有313，所以313=q ．经检验素数对)313,5(合乎要求．若q p ,都不等于2和5，则有1155|--+q p pq ，故SO RQNFEDCBA P)(m od 05511p q p ≡+--． ①由Fermat 小定理，得 )(m od 151p p ≡- ， ②故由①，②得)(m od 151p q -≡-． ③设)12(21-=-r p k，)12(21-=-s q l， 其中s r l k ,,,为正整数． 若l k ≤，则由②，③易知)(mod 1)1()5(5)5(1112121)12)(12(2)12(21)12(2p r r q s r s p s l k l k l -≡-≡==≡=----------，这与2≠p 矛盾！所以l k >．同理有l k <，矛盾！即此时不存在合乎要求的),(q p ． 综上所述，所有满足题目要求的素数对),(q p 为)3,2(，)2,3(，)5,2(，)2,5(，)5,5(，)313,5(及)5,313(．三、设m ，n 是给定的整数，n m <<4，1221+n A A A Λ是一个正2n +1边形，{}1221,,,+=n A A A P Λ．求顶点属于P 且恰有两个内角是锐角的凸m 边形的个数．解 先证一个引理：顶点在P 中的凸m 边形至多有两个锐角，且有两个锐角时，这两个锐角必相邻．事实上，设这个凸m 边形为m P P P Λ21，只考虑至少有一个锐角的情况，此时不妨设221π<∠P P P m ，则)13(2122-≤≤>∠-=∠m j P P P P P P m m j ππ，更有)13(211-≤≤>∠+-m j P P P j j j π．而321P P P ∠+11P P P m m -∠>π，故其中至多一个为锐角，这就证明了引理． 由引理知，若凸m 边形中恰有两个内角是锐角，则它们对应的顶点相邻．在凸m 边形中，设顶点i A 与j A 为两个相邻顶点，且在这两个顶点处的内角均为锐角．设i A 与j A 的劣弧上包含了P 的r 条边（n r ≤≤1），这样的),(j i 在r 固定时恰有12+n 对．（1） 若凸m 边形的其余2-m 个顶点全在劣弧j i A A 上，而j i A A 劣弧上有1-r 个P 中的点，此时这2-m 个顶点的取法数为21--m r C ．（2） 若凸m 边形的其余2-m 个顶点全在优弧j i A A 上，取i A ，j A 的对径点i B ，j B ，由于凸m 边形在顶点i A ，j A 处的内角为锐角，所以，其余的2-m 个顶点全在劣弧j i B B 上，而劣弧j i B B 上恰有r 个P 中的点，此时这2-m 个顶点的取法数为2-m rC ．所以，满足题设的凸m 边形的个数为))()()(12()12()()12(11111111121211221∑∑∑∑∑==--+---=-=--=----+-+=⎪⎭⎫⎝⎛++=++nr nr m rm r m r m r n r m r n r m r nr m rm r C C C C n C C n CCn))(12(111--+++=m n m n C C n ．四、给定整数3≥n ，实数n a a a ,,,21Λ满足 1min 1=-≤<≤j i nj i a a ．求∑=nk k a 13的最小值．解 不妨设n a a a <<<Λ21，则对n k ≤≤1，有k n a a a a k k n k n k 2111-+≥-≥++-+-，所以()∑∑=-+=+=nk kn knk ka a a 13131321()()()∑=-+-+-+⎪⎭⎫ ⎝⎛++-+=n k k n k kn k k n k a a a a a a 121211414321 ()∑∑==-+-+≥+≥n k nk kn k k n a a 13131218181． 当n 为奇数时，222113313)1(412221-=⋅⋅=-+∑∑-==n i k n n i nk ． 当n 为偶数时，32113)12(221∑∑==-=-+n i nk i k n⎪⎪⎪⎭⎫ ⎝⎛-=∑∑==21313)2(2ni n j i j)2(4122-=n n ． 所以，当n 为奇数时，2213)1(321-≥∑=n a nk k，当n 为偶数时，)2(3212213-≥∑=n n a nk k，等号均在n i n i a i ,,2,1,21Λ=+-=时成立． 因此，∑=nk k a 13的最小值为22)1(321-n （n 为奇数），或者)2(32122-n n （n 为偶数）． 五、凸n 边形P 中的每条边和每条对角线都被染为n 种颜色中的一种颜色．问：对怎样的n ，存在一种染色方式，使得对于这n 种颜色中的任何3种不同颜色，都能找到一个三角形，其顶点为多边形P 的顶点，且它的3条边分别被染为这3种颜色？解 当n 3≥为奇数时，存在合乎要求的染法；当n 4≥为偶数时，不存在所述的染法。

数学奥林匹克高中训练题(19)第一试、选择题(本题满分 36分，每小题6分) 1.(训练题 24)对于每一对实数x,y ,函数f 满足方程f (x • y)「f (x)「f (y) -T xy ，且fl 仁•那么，f(n) =n(n =1)的整数n 的个数共有(B)个. (B)1 (C)2 (D) (A)0 2 .(训练题24)有六个座位连成一排，三人就座，恰有两个空位相邻的排法种数为 (A)72 (B)96 (C) 48 (D) 3 .(训练题24)在一次体育比赛中，红白两队各有 5名队员参加，比赛记分办法是： 几名就为本队得几分，且每个队员的得分均不同，得分少的队获胜，则可能获胜的分数是 3 (A).以上都不对队员在比赛中获第(C).27 (A)29 (B)28 4.(训练题24)现有下面四个命题： ① 底面是正多边形，其余各面都是等腰三角形的棱锥是正棱锥. ② 底面是正三角形，相临两侧面所成二面角都相等的三棱锥是正三棱锥. ③ 有两个面互相平行，其余四个面都是全等的等腰梯形的六面体是正四棱台. ④ 有两个面互相平行，其余各个面是平行四边形的多面体是棱柱. 其中，正确的命题的个数是 (A) 3 (B) (D). 2 (C) (C) (D) (D) 13 5.(训练题24)设f : N > N , 且对所有正整数 有 f(n 1) f(n), f( f( rj) 3n .f (1997)的值为(C). (A)1997 (B)1268 (C)3804 (D)5991-训练题24唱爲:;胯豐 的解(x, y)共有(B)组. (A)4 二、填空题 (B)2 (C)1 (D) (本题满分 54分，每小题9分) 1.(训练题 24)数列｛a n ｝的前 14 项是 4, 6, 9, 10, 14, 15, 21, 22, 25, 26, 33,34, 35, 38，….按此规律，则2.(训练题24)函数f (x)二(長- ~^)( J x T + r 1——)丄的值域是v xJ x —1 x(0,1)3.(训练题24)方程x^1 x ； /I 2 x.二 1 远的解是—2 ■ 36 714.（训练题24）若方程x2（^2i）x 3m -i =0（m R）有一实根、一虚根，则此虚根是2i—25 .（训练题24）平面上有四点A, B, C, D,其中代B为定点，且AB = J3,C, D为动点，且AD DC =|BCT ，记S咎BD=T为也BCD的面积.贝U S2+T2的取值范围是2、「3 -3 2 2 7S2T2：4 811 1 16.（训练题24）使不等式——- - a-1995—对一切自然数n都成立的最小自然数n+1 n+2 2n+1 3a 是1997 ______ .第二试2 2一、（训练题24）（本题满分25分）已知F1, F2是椭圆笃=1（a b 0）的左、右焦点，c为半焦距，a b弦AB过焦点F2•求■ F1AB的面积的最大值.n、（训练题24）（本题满分25分）若X j・0,二人=1, x, x-i, n，求证:三、（训练题24）（本题满分35分）已知ABC是等腰三角形，AB=AC,CD是腰AB上的高线，CD1的中点为M,AE _ BM于E, AF _CE于F •求证：AF _丄AB .3四、（训练题24）（本题满分35分）46个国家派代表队参加一次国际竞赛，比赛共4个题，结果统计如下：做对第一题的选手235人，做对第一、二的选手59人，做对第一、三的选手29人，做对第一、四的选手15人，全做对的3人•存在这样的选手，他做对了前三题，但没有做对第四题•求证：存在一个国家，这个国家派的选手中至少有4个人，他们只做对了第一题.。