三视图与立体图形

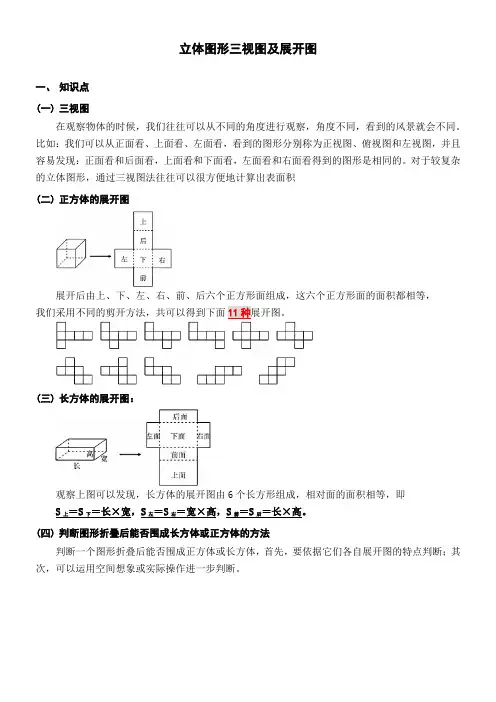
立体图形三视图及展开图一、知识点(一)三视图在观察物体的时候，我们往往可以从不同的角度进行观察，角度不同，看到的风景就会不同。

比如：我们可以从正面看、上面看、左面看，看到的图形分别称为正视图、俯视图和左视图，并且容易发现：正面看和后面看，上面看和下面看，左面看和右面看得到的图形是相同的。

对于较复杂的立体图形，通过三视图法往往可以很方便地计算出表面积(二)正方体的展开图展开后由上、下、左、右、前、后六个正方形面组成，这六个正方形面的面积都相等，我们采用不同的剪开方法，共可以得到下面(三)长方体的展开图：观察上图可以发现，长方体的展开图由6个长方形组成，相对面的面积相等，即S上＝S下＝长×宽，S左＝S右＝宽×高，S前＝S后＝长×高。

(四)判断图形折叠后能否围成长方体或正方体的方法判断一个图形折叠后能否围成正方体或长方体，首先，要依据它们各自展开图的特点判断；其次，可以运用空间想象或实际操作进一步判断。

二、题型(一)展开图与对立面【例1.1】水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示，如下图，是一个正方体的平面展开图，若图中的“似”表示正方体的前面，“锦”表示右面，“程”表示下面。

则“祝”、“你”、“前”分别表示正方体的________________________。

【答案】后面、上面、左面【解析】易知“你”、“程”相对，“前”、“锦”相对，“祝”、“似”相对，因此“祝”、“你”、“前”分别表示正方体的后面、上面、左面。

【例1.2】一个数学玩具的包装盒是正方体，其表面展开图如下。

现在每方格内都填上相应的数字。

已知将这个表面展开图沿虚线折成正方体后，相对面的两数之和为“3”，则填在A、B、C内的三个数字依次是___________。

【答案】3、1、2【解析】面上的数是“0”，与“B”相对的面上的数是“2”，与“C"相对的面上的数是“1”。

三视图与立体图形的刻画在我们的日常生活和学习中，常常会遇到各种各样的立体图形。

无论是建筑设计中的高楼大厦，还是机械制造中的精密零件，又或者是美术创作中的雕塑作品，立体图形都扮演着重要的角色。

而要准确地理解和描绘这些立体图形，三视图是一个非常有用的工具。

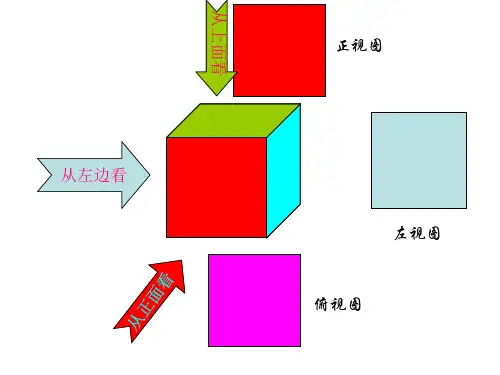
什么是三视图呢？简单来说，三视图就是从三个不同的方向观察一个立体图形所得到的平面图形。

这三个方向通常是正前方（主视图）、正上方（俯视图）和正左方（左视图）。

通过这三个视图，我们可以在平面上完整地刻画一个立体图形的形状和尺寸。

想象一下，你面前有一个长方体盒子。

当你从正前方看它时，看到的是一个长方形，这就是主视图；当你从正上方看它时，看到的是一个更大的长方形，这就是俯视图；而当你从正左方看它时，又会看到一个长方形，这就是左视图。

这三个视图结合起来，就能让我们清楚地知道这个长方体盒子的大小和形状。

三视图的绘制有着严格的规则。

在主视图中，我们要反映出立体图形的长和高；在俯视图中，要反映出长和宽；在左视图中，则要反映出宽和高。

而且，三个视图之间有着密切的对应关系，比如主视图和俯视图的长相等，主视图和左视图的高相等，俯视图和左视图的宽相等。

那么，三视图对于我们理解和刻画立体图形到底有什么重要意义呢？首先，三视图能够帮助我们准确地想象出立体图形的形状。

当我们看到一个复杂的立体图形的三视图时，通过对三个视图的观察和分析，我们可以在脑海中逐步构建出这个立体图形的三维形象。

这对于设计师、工程师等需要进行空间想象的职业来说，是一项非常重要的能力。

其次，三视图可以清晰地表达立体图形的尺寸和比例关系。

在制造和生产中，精确的尺寸是至关重要的。

通过三视图上标注的尺寸，工人可以准确地制造出符合要求的零件或产品。

再者，三视图为交流和沟通提供了便利。

当不同的人需要讨论一个立体图形时，如果只是口头描述，很容易产生误解。

而有了三视图，大家就可以基于共同的图形进行交流，大大提高了沟通的效率和准确性。

三视图与立体图形表示与计算在工程设计和制图领域中，三视图与立体图形表示与计算是非常重要的技术。

通过三视图的绘制和立体图形的计算，可以准确地描述和表达物体的形状、尺寸和位置关系。

本文将介绍三视图和立体图形的概念、表示方法和计算原理，并探讨其在工程领域中的应用。

一、三视图的概念和表示方法三视图是指根据物体的外形和结构特征，在不同的视角下绘制出物体的正视图、俯视图和侧视图。

正视图是物体在水平平面上的投影，俯视图是物体在垂直平面上的投影，侧视图是物体在侧面的投影。

通过这三个视图，可以全面了解物体的外形和尺寸。

在绘制三视图时，需要注意以下几点。

首先，要确定一个基准面作为绘制的参考面，通常选择前、顶、右作为正视图、俯视图和侧视图的绘制面。

其次，要掌握正确的投影规律和投影关系，保持视角的一致性。

最后，要注意三视图之间的协调性和一致性，确保在不同视角下所绘制的视图相互匹配。

二、立体图形的概念和表示方法立体图形是指具有三维形态的物体，与平面图形不同，立体图形具有长度、宽度和高度三个方向上的尺寸。

为了准确地表示和描述立体图形，常用的表示方法有线框图、透视图和三维模型等。

线框图是通过绘制物体表面的轮廓线来表示立体图形的方法。

在绘制线框图时，需要注意轮廓线的粗细和颜色，以及物体各部分之间的连接关系。

透视图是通过在透视投影下观察物体，将其立体形态呈现在平面上。

透视图能够更加真实地还原物体的外观，但需要掌握透视投影的原理和技巧。

除了线框图和透视图外，还可以利用三维建模软件来创建立体图形的三维模型。

三维模型可以在计算机中进行旋转、缩放和移动等操作，方便观察和分析物体的各个方面和细节。

三维建模软件在现代工程设计和制图中得到了广泛应用。

三、立体图形的计算在工程设计和制图中，有时需要根据已知的三视图来计算物体的其他尺寸和几何特征。

立体图形的计算可以通过几何关系和数学运算来实现。

对于简单的立体图形，可以利用几何关系和图形的相似性来进行计算。

怎样将几何的三视图还原为立体几何图形
三视图还原立体几何简单与否因人而异，空间想象力强的人，一眼便能看出是什么样的图形。

我就觉得这种题目还是挺简单的，哈哈。

首先我给你几个最常见的例子。

1.三面都是长方，就是长方体；2.上面看圆，两个侧面看长方，就是圆柱；3.上面看圆，两侧面看三角，就是圆锥；4.上面看多边形，两侧面看三角，就是棱锥；5.上面看多边形，两侧看长方，就是棱柱；6.上面看圆，两侧看梯形，就是圆台；7.三面都是圆，就是球。

其次要注意的是，三视图显示了图形的长宽高，从上方看的图显示了长宽或者直径之类的东西，从侧面看的图显示了长和高，或者宽和高，或者直径和高之类的。

第三要是你空间想象力不强，那么就得多练习。

至于方法，我觉得多锻炼逆向思维能力是最好的。

你可以随便想象出一个立体图形，然后自己给那个图形画三视图，然后再只看你的三视图想象你刚才想的图形，反复练习，多总结，我想你会有启发、收获的。

最后说说三视图的作用。

要是你单看三视图，这个东西高考也不会考，看似没有用，实际上它是很有用的。

它为你以后的立体几何题的分析打下了一定的基础，是一个融入于解题思路中的方法。

综上所述，建议你好好练习三视图。

立体几何和三视图一、知识点回顾1、空间几何体的三视图定义三视图：正视图（光线从几何体的前面向后面正投影）；侧视图（从左向右）、 俯视图（从上向下）注：正视图反映了物体上下、左右的位置关系，即反映了物体的高度和长度； 俯视图反映了物体左右、前后的位置关系，即反映了物体的长度和宽度；侧视图反映了物体上下、前后的位置关系，即反映了物体的高度和宽度。

▲长对正，高平齐 ，宽相等2、柱体、锥体、台体的表面积与体积（1）几何体的表面积为几何体各个面的面积的和。

（2）特殊几何体表面积公式（c 为底面周长，h 为高，'h 为斜高，l 为母线）ch S =直棱柱侧面积 rh S π2=圆柱侧 '21ch S =正棱锥侧面积 rl S π=圆锥侧面积')(2121h c c S +=正棱台侧面积l R r S π)(+=圆台侧面积()l r r S +=π2圆柱表 ()l r r S +=π圆锥表 ()22R Rl rl r S +++=π圆台表（3）柱体、锥体、台体的体积公式V Sh =柱 2V S h r h π==圆柱 13V S h=锥 h r V 231π=圆锥'1()3V S S h =+台'2211()()33V S S h r rR R h π=++=++圆台二、专题讲解1、空间角问题（1）直线与直线所成的角 ①两平行直线所成的角：规定为 0。

②两条相交直线所成的角：两条直线相交其中不大于直角的角，叫这两条直线所成的角。

③两条异面直线所成的角：过空间任意一点O ，分别作与两条异面直线a ，b 平行的直线b a '',，形成两条相交直线，这两条相交直线所成的不大于直角的角叫做两条异面直线所成的角。

（2）直线和平面所成的角①平面的平行线与平面所成的角：规定为 0。

②平面的垂线与平面所成的角：规定为90。

③平面的斜线与平面所成的角：平面的一条斜线和它在平面内的射影所成的锐角，叫做这条直线和这个平面所成的角。

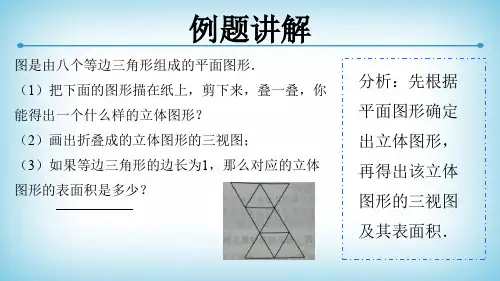
三视图与立体图形的区别及如何看三视图
三视图是观测者从三个不同位置观察同一个空间几何体而画出的图形.
将人的视线规定为平行投影线，然后正对着物体看过去，将所见物体的轮廓用正投影法绘制出来该图形称为视图.一个物体有六个视图：从物体的前面向后面投射所得的视图称主视图——能反映物体的前面形状，从物体的上面向下面投射所得的视图称俯视图——能反映物体的上面形状，从物体的左面向右面投射所得的视图称左视图——能反映物体的左面形状，还有其它三个视图不是很常用.三视图就是主视图、俯视图、左视图的总称.
一个视图只能反映物体的一个方位的形状，不能完整反映物体的结构形状.三视图是从三个不同方向对同一个物体进行投射的结果，另外还有如剖面图、半剖面图等做为辅助，基本能完整的表达物体的结构.
立体图能在一个投影图上把物体的三个方向（如前面、上面、侧面）的形状表示出来，图形具有较好的立体感.而三视图的每一张图并没有立体效果.。

第六章几何图形初步
§6.2立体图形的三视图
【知识要点】
1．三视图是从三个正向视角看几何体，所得到的平面图形．主视图：从前往后看，是从前往后的正投影；
左视图：从左往右看，是从左往右的正投影；
俯视图：从上往下看，是从上往下的正投影；
2．常见几何体的三视图如下表所示：
一般,将看得见的轮廓线画成实线，看不见的轮廓线画成虚线．类型一投影法画三视图
例1请画出下列几何体的三视图．
（1）（2）（3）
练习1请画出下列几何体的三视图．
（1）（2）（3）（4）
类型二从不同方向看立体图形
例2如图是由5个相同的小正方体搭成的几何体，从上面看到的形状图是( )
A．B．C．D．
练习2请画出下列几何体的三视图．
（1）（2）
（3） （4）
类型三 根据不同方向看到的图形还原几何体的形状
例3如图用若干小正方体搭成的几何体的三视图，则原几何体是( )
A ．
B ．
C ．
D ．
练习3（1）如图是几个小正方体搭成的几何体的三视图，则原几何体中小正方体的个数为 ；
（2）若正方体的棱长为1，则还原后的几何体的表面积为对少？
主视图
左视图
俯视图
俯视图
左视图
主视图
练习4如图是几个小正方体搭成的几何体的俯视图，其中数字表示从上面看一列有几个小正方体，请画出主视图和左视图．
2
21
1
主视图
左视图。

七年级苏教版数学复习要点考点专题四：立体图形及三视图知识点一常见立体图形1．立体图形与平面图形①有些几何图形（如长方体、正方体、圆柱、圆锥、球等）的各部分不都在同一平面内，它们是立体图形．②有些几何图形（如线段、角、三角形、长方形、圆等）的各部分都在同一平面内，它们是平面图形．3．常见立体图形的分类曲面体圆柱、圆锥、球体按是否有顶点是棱柱、棱锥、圆锥否圆柱、球体总结：在对几何体分类时首先确定分类的标准，分类标准不同，结果也就不同，不论选择哪种分类标准，都要做到不重、不漏.4、点、线、面、体体：长方体、正方体、圆柱、圆锥、球、棱柱、棱锥都是几何体，几何体也称体．面：包围着体的是面．面有平面和曲面两种．线：面和面相交的地方形成线．点：线和线相交的地方是点．用运动的观点来看：点动成线、线动成面、面动成体．例1（中山区期末）三角形ABC绕BC旋转一周得到的几何体为()A．B．C．D．【解答】解：由图形的旋转性质，可知ABC旋转后的图形为C，故选：C．例2（邳州市期末）如图，在下列图形中，绕铅垂线旋转一周可得到如图所示几何体的是()A．B．C．D．【解答】解：A、是直角梯形绕高旋转形成的圆台，故A正确；B、是直角梯形绕底边的腰旋转形成的圆柱加圆锥，故B错误；C、绕直径旋转形成球，故C错误；D、绕直角边旋转形成圆锥，故D错误．故选：A．例3（皇姑区期末）下面是一个正方体，用一个平面去截这个正方体截面形状不可能为下图中的()A．B．C．D．【解答】解：无论如何去截，截面也不可能有弧度，因此截面不可能是圆．故选：D．知识点二几何体的表面展开图1．展开图：有些几何体的表面可以展开成平面图形，这个平面图形称为相应几何体的表面展开图.2．常见立体图形的平面展开图（1）圆柱的表面展开图是两个相同的圆面和一个长方形组成的；（2）圆锥的表面展开图是由一个圆面和一个扇形组成的；（3）棱柱的表面展开图是由两个相同的多边形和一个长方形组成的，侧面展开图是一个长方形。