课题绝对值三角不等式

格式：doc
大小：296.50 KB
文档页数：4

下载文档原格式

/ 4

课题：绝对值三角不等式

课题：绝对值三角不等式红岭中学隗双和教学目标：知识与技能：了解绝对值三角不等式的含义，理解绝对值三角不等式公式及推导方法，会进行简单的应用。

过程与方法：充分运用观察、类比、猜想、分析证明的数学思维方法，体会转化和数形结合的数学思想，并能运用绝对值三角不等式公式进行推理和证明。

情感、态度与价值观：体验不等式的美感，提高推理能力，增强学习兴趣。

能运用所学的知识，正确地解决的实际问题.教学重点：绝对值三角不等式的含义，绝对值三角不等式的理解和运用。

教学难点：绝对值三角不等式的发现和推导、取等条件。

授课类型：新授课课时安排：1课时教具：多媒体辅助。

教学过程：一、复习引入：关于含有绝对值的不等式的问题，主要包括两类：一类是解不等式，另一类是证明不等式。

本节课探讨不等式证明这类问题。

1．请同学们回忆一下绝对值的意义。

⎪⎩⎪⎨⎧<-=>=0000x x x x x x ，如果，如果，如果。

几何意义：在数轴上，一个点到原点的距离称为这个点所表示的数的绝对值。

即2．证明一个含有绝对值的不等式成立，除了要应用一般不等式的基本性质之外，经常还要用到关于绝对值的和、差、积、商的性质：（1）a a ≥，当且仅当0≥a 时等号成立，.a a -≥当且仅当0≤a 时等号成立。

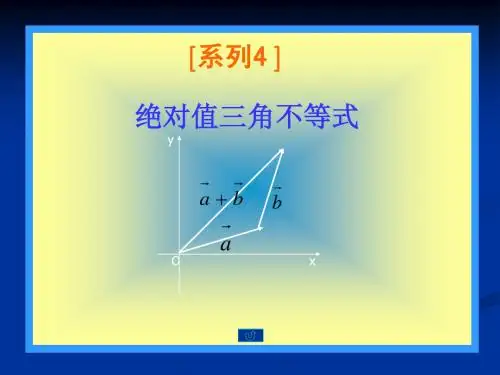
（2）2a a =，（3）b a b a ⋅=⋅，（4）)0(≠=b baba 那么?b a b a +=+?b a b a +=-二、讲解新课：结论：a b a b ++≤（当且仅当0ab ≥时，等号成立.）已知,a b 是实数，试证明：a b a b ++≤（当且仅当0ab ≥时，等号成立.）探究: ,,a b a b +, 之间的什么关系?b a -aba b+方法一：证明:10 .当ab ≥0时, 20. 当ab <0时,综合10,20知定理成立.方法二：分析法，两边平方（略）定理1 如果,a b 是实数，则a b a b ++≤（当且仅当0ab ≥时，等号成立.）（1）若把,a b 换为向量,a b 情形又怎样呢？（2）若把,a b 换为复数12,z z ，结论：1212z z z z ++≤成立吗？根据定理1，有b b a b b a -+≥-++，就是，a b b a ≥++。

第一讲(二)(1)：绝对值三角不等式

定理2: 如果a,b,c是实数,则
|a-c||a-b|+|b-c|
当且仅当(a-b)(b-c)0时,等号成立. 证明:根据定理1,有: |a-c|=|(a-b)+(b-c)| |a-b|+|b-c| 当且仅当(a-b)(b-c)0时,等号成立.
9
知识应用
例1 已知 0， | x a | ，| y b | . 求证：| 2 x 3 y 2a 3b | 5 .
例:解不等式 | 5x-6 | < 6 – x
（0，2）
解不等式 | 5x-6 | < 6 – x
有更一般的结论：
|f(x)|<g(x) |f(x)|>g(x) -g(x)<f(x)<g(x) f(x)>g(x) 或f(x)<-g(x)
-2 0 2 -a a 类比：|x|<3的解 |x|>3 的解 -a<x<a 归纳：|x|<a（a>0)
ቤተ መጻሕፍቲ ባይዱ
|x|<-2的解
|x|>a (a>0) |x|>-2的解 X>a 或 x<-a
引伸：
如果把|x|<2中的x换成“x-1”,也就是 | x-1 | <2如何解？
如果把|x|>2中的x换成“3x-1”,也就是
巩固练习：
求下列不等式的解集
① |2x+1|<5
② 3|1-4x|>9 ③ |4x|<-1
（-3，2）（-∞，-1/2）∪（1，+ ∞）

R
④ |x2-5x|>-6
⑤ 3<| 2x+1 | <5

绝对值三角不等式课件

证明:∵m 等于|a|,|b|和 1 中最大的一个,|x|>m,
|| > ≥ ||
|| > ||,

||
||
>

≥
||
∴
⇒
∴ + 2 ≤
+ 2 = +
2

||
|| > |b|.
|| > ≥ 1
||
2
|| ||
<
+ 2 =2.故原不等式成立.
2
||
||
∴-4≤y≤4.
∴yma x=4,y min =-4.
迁移与应用
如果关于 x 的不等式|x-3|+|x-4|<a 的解集为空集,求参数 a
的取值范围.
解:只要 a 不大于|x-3|+|x-4|的最小值,则|x-3|+|x-4|<a 的解集
为空集,而|x-3|+|x-4|=|x-3|+|4-x|≥|x-3+4-x|=1,
=|(x-a)(x+a-1)|
=|x-a||x+a-1|
<|x+a-1|
=|Байду номын сангаас-a+2a-1|
≤|x-a|+|2a-1|
<1+|2a|+1
=2(|a|+1),
∴|f(x)-f(a)|<2(|a|+1).
迁移与应用
已知 f(x)=x2 -2x+7,且|x-m|<3,求证:|f(x)-f(m)|<6|m|+15.

绝对值三角不等式PPT课件

误区警示
例求证：1＋|a＋|a＋b|b|≤1＋|a||a|＋1＋|b||b|.
【错证】 ∵ |a ＋ b|≤|a| ＋ |b|,1 ＋ |a ＋ b|>0，
∴
|a＋b| 1＋|a＋b|
≤
|a|＋|b| 1＋|a＋b|
＝
|a| 1＋|a＋b|
＋
1＋||ba＋| b|≤1＋|a||a|＋1＋|b||b|.
y x a a y b M a . 2M 2 a
典例讲评
例4.已知 | a | 1, | b | 1, 求证 a b 1
证明：a b
1
(a b)2
1 ab
1
1 ab
(1 ab)2
a2 2ab b2 1 2ab a2b2
变式训练 2 设 a，b∈R，ε>0，|a|<4ε， 2
|b|<3ε. 求证：|4a＋3b|<3ε. 证明：∵|a|<4ε，|b|<23ε. ∴|4a＋3b|≤|4a|＋|3b|
＝4|a|＋3|b|<4·4ε＋3·23ε＝3ε.
例3 已知a，b，c是实数，函数f(x)＝ax2＋ bx ＋ c ， g(x) ＝ ax ＋ b ，当－ 1≤x≤1 时， |f(x)|≤1. (1)证明：|c|≤1； (2)证明：当－1≤x≤1时，|g(x)|≤2. 【思路点拨】对于(1)用一般到特殊的思想，即c＝f(0)．对于(2)分a>0，a＝0，a<0根据函数的单调性讨论．
【解析】 (1)法一：特殊值法：取x＝1，y ＝－2，则满足xy＝－2<0，这样有|x＋y|＝|1－2|＝1， |x－y|＝|1－(－2)|＝3， |x|＋|y|＝3，||x|－|y||＝1， ∴选项C成立，A，B，D不成立．法二：由xy<0得x，y异号，易知|x＋y|<|x－y|，|x－y|＝|x|＋|y|， |x－y|>||x|－|y||， ∴选项C成立，A、B、D不成立．

5.2绝对值三角不等式A 课件(人教A版选修4-5)

探究你能比较 a b 与 a b
a b a b a b a b a b a b
之间的大小关
当ab>0时，
当ab<0时，当ab=0时，
你能将上述情况综合起来吗？
定理1
如果a,b是实数，则当且仅当
a b a b
ab 0 时，等号成立。
如果把定理1中的实数a,b分别换为向量
例2
两个施工队分别被安排在公路沿线的两个地点施工，这两个地点分别位于公路路牌的第10km和第20km 处。现要在公路沿线建两个施工队的共同临时生活区，每个施工队每天在生活区和施工地点之间往返一次。要使两个施工队每天往返的路程之和最小，生活区应该建于何处？
分析：如果生活区建于公路路牌的第xkm处，两个施工队每天往返的路程之和为S(x)km,那么 S x 2 x 10 x 20 于是，上面的问题就化归为数学问题：当x取何值时，函数 S x 2 x 10 x 20 取得最小
10 x 20
所以，生活区建于两个施工地点之间的任何一个位置时，都能使两个施工队每天往返的路程之和最小。
70
60
s x = 2 x-10 + x-20
50
40
30
20
10
-60
-40
-20
10
20
40
60
80
100
-10
-20
-30

值。这个问题可以应用绝对值不等式的性质来解。
解：设生活区应该建于公路路牌的第xkm处，两个施工队每天往返的路程之和为S(x)km,则因为
S x 2 x 10 x 20

绝对值三角不等式

绝对值三角不等式
单击添加副标题
汇报人：
目录
01
单击添加目录项标题
02
03
绝对值三角不等式的证明
04
05绝Biblioteka 值三角不等式的推广绝对值三角不等式的定义绝对值三角不等式的应用
01
添加章节标题
02
绝对值三角不等式的定义
绝对值三角不等式的表述
绝对值三角不等式是描述两个实数和b之间关系的不等式
绝对值三角不等式的形式为|b|≤||+|b|
在解析几何中的应用
确定平面上的点：通过绝对值三角不等式可以确定平面上的点与原点的距离和角度。
确定直线的位置：通过绝对值三角不等式可以确定直线与原点的距离和角度从而确定直线的位置。
确定平面的位置：通过绝对值三角不等式可以确定平面与原点的距离和角度从而确定平面的位置。
确定曲面的位置：通过绝对值三角不等式可以确定曲面与原点的距离和角度从而确定曲面的位置。
在不等式证明中的应用
绝对值三角不等式是证明不等式的重要工具
可以用于证明一些常见的不等式如均值不等式、柯西不等式等
在解决一些数学问题中如求最值、证明不等式等也可以使用绝对值三角不等式
在解决一些实际问题中如物理、工程等也可以使用绝对值三角不等式进行计算和证明
05
绝对值三角不等式的推广
绝对值三角不等式的形式：||+|b|≥|+b|
利用绝对值的性质证明绝对值三角不等式：通过比较||+|b|和|+b|的大小得出绝对值三角不等式的结论
利用三角形的性质证明
三角形两边之和大于第三边三角形两边之差小于第三边三角形两边之积大于第三边三角形两边之积小于第三边三角形两边之积等于第三边三角形两边之积等于第三边

绝对值三角形不等式公式推导

绝对值三角形不等式公式推导绝对值三角形不等式公式推导一、引言绝对值三角形不等式是解决绝对值不等式问题的基本工具之一，在数学中有着广泛的应用。

它主要用于解决包括代数和几何问题在内的多种数学问题。

在本文中，我将深入探讨绝对值三角形不等式的导出过程，并结合具体例子进行解释，以帮助读者更好地理解和掌握这一重要的数学概念。

二、绝对值三角形不等式公式的基本定义为了全面了解绝对值三角形不等式的公式推导过程，我们需要先了解其基本定义。

假设a和b是实数，那么绝对值三角形不等式可以表达为：|a + b| ≤ |a| + |b|这一不等式是指，两个数的绝对值之和不大于其各自绝对值的和。

这一概念对于处理绝对值的复杂运算问题起到了重要的作用。

接下来，我将详细介绍绝对值三角形不等式的推导过程，帮助读者全面理解这一概念。

三、绝对值三角形不等式公式的推导过程为了推导绝对值三角形不等式的公式，我们可以利用数轴的性质和绝对值的定义进行推导。

我们假设a和b是实数且a≥0，b≥0。

现在，我们来看一下具体的推导过程：1. 我们假设a≥0，b≥0。

根据数轴的性质，a和b对应的点分别为A 和B，那么|a|和|b|分别表示点A和B到原点的距离。

2. 现在，我们考虑点C，它表示a+b对应的实数。

根据数轴的性质，我们可以知道|a+b|表示点C到原点的距离。

3. 根据三角形两边之和大于第三边的性质，我们可以得出结论：|a + b| ≤ |a| + |b|通过以上推导过程，我们可以得出绝对值三角形不等式的公式。

这一推导过程清晰地展现了绝对值三角形不等式的基本原理和应用。

四、绝对值三角形不等式公式的应用举例为了更好地理解绝对值三角形不等式的应用，我们可以通过具体的例子来说明。

例1：求解|2x + 1| ≤ 5的解集。

解：根据绝对值三角形不等式的公式，我们可以得出：|2x + 1| ≤ 5-5 ≤ 2x + 1 ≤ 5-6 ≤ 2x ≤ 4-3 ≤ x ≤ 2|2x + 1| ≤ 5的解集为-3 ≤ x ≤ 2。

高二数学人选修课件绝对值三角不等式

03
一元二次绝对值三
角不等式
一元二次绝对值不等式解法
零点分段法
通过找出不等式中绝对值符号内表达式的零点，将数轴分为若干个区间，然后在每个区间内去掉绝对值符号进行讨论，最后综合各个区间的解得到原不等式的解集。
平方去绝对值法
对于形如$|f(x)|>g(x)$或$|f(x)|<g(x)$的不等式，可以通过平方去掉绝对值符号，转化为一般的不等式进行求解。但需要注意，平方时可能会扩大或缩小原不等式的解集，因此需要对解集进行检验。
排序不等式
对于两组实数序列{ai}和{bi}，若a1 ≤ a2 ≤ ... ≤ an，b1 ≤ b2 ≤ ... ≤ bn，则有∑ai*bi ≥ ∑aj*bk（其中j, k为任意排列），当且仅当ai与bi一一对应时取等号。排序不等式可用于解决一些与顺序有关的问题。
均值不等式
对于任意正实数a, b，有√(ab) ≤ (a + b)/2 ≤ √[(a^2 + b^2)/2]。均值不等式可用于解决一些与平均值有关的问题。
02
一元一次绝对值三
角不等式
一元一次绝对值不等式解法
零点分段法
根据绝对值的定义，将绝对值不等式转化为分段函数，然后分别求解每一段的不等式。
几何意义法
利用绝对值的几何意义，将绝对值不等式转化为数轴上的距离问题，从而进行求解。
一元一次三角不等式解法
三角函数性质法
利用三角函数的性质，如周期性、奇偶性、单调性等，将三角不等式转化为普通的不等式进行求解。
三角函数的单调性
利用三角函数的单调性，可以求解一些简单的三角不等式。例如，对于$sin x geq frac{1}{2}$，由于$sin x$在$[0, frac{pi}{2}]$上单调递增，因此解集为$[2kpi + frac{pi}{6}, 2kpi + frac{5pi}{6}]$（$k in Z$）。

绝对值三角不等式

∴|x－a|＋|y－a|＜2m，
又∵|(x－a)－(y－a) | ≤|x－a|＋|y－a|，
∴|x－y|＜2m，但反过来不一定成立，
如取 x ＝ 3 ， y ＝ 1 ， a ＝－ 2 ， m ＝ 2.5 ， |3 － 1| ＜
2×2.5，但|3－(－2)|＞2.5，|1－(－2)|＞2.5，
∴|x－y|＜2m不一定有|x－a|＜m且|y－a|＜m，故
证明: 当ab0时, ab=|ab|
|a+b| a b
2
2
2
a 2ab b
2
2
| a | 2 | ab | | b |

2
| a | | b | a b
当 ab < 0 时, ab |ab|,
|a+b| a b a 2ab b
之间的距离，即线段AB的长度
用恰当的方法在数轴上把 |a|, |b|, |a+b|表示出来，
同学们观察能发现它们之间有什么关系？ ab>0 O a

a + b b
x
a+ b

b

a O a+b

x
b

a+b

O a

ab<0 x

a O
b

x
定理1: 如果a, b是实数,
则 | a + b | | a | + | b |,
当且仅当 ab 0 时,等号成立.
如果把定理1中的实数a,b分别换为向量 a , b,
能得出什么结果?
定理1的几何意义

绝对值的三角不等式公式证明

绝对值的三角不等式公式证明
绝对值三角不等式是一个非常强大且非常有用的数学公式，它可以帮助我们精确地解决很多问题。

它的数学形式可以表述为：|x-y| < = a+b，其中x、y、a、b 都是实数，|x-y|表示x-y的绝对值。

绝对值三角不等式的证明由单射定理开始，它是数学中一个基本定理，其定义可以表达为：如果a＞b，则存在c＞0，使得a - c < b。

根据这个定理，关于x、y、a、b之间的关系可以写成更加清楚的等式形式：a-b<x-y < a+b。

接下来，假设y-x>0，也就是说x<y，此时有y-x<a+b，带入单射定理可得a-(y-x)<b，也就是说a-y+x < b，整理得x-y<a+b，故可证|x-y|<=a+b。

同理，如果y-x<0，也就是说x>y，此时有x-y<a+b，根据单射定理可得a-(x-y)<b，整理得a-x+y<b，故可证|x-y|<=a+b。

综上所述，可以看出绝对值三角不等式的证明基于单射定理，从而为我们提供了一个精确地解决数学问题的有效方法。

正是由于绝对值三角不等式的重要性和有效性，它被广泛用于各种数学领域中，如超越几何、微积分、概率论等。

如何巧用绝对值三角不等式解题

绝对值三角不等式：||a |－|b ||≤|a ±b |≤|a |＋|b |.显然，当且仅当ab ≥0时等号成立.由该不等式可推出定理1：如果a ，b 是实数，则|a ＋b |≤|a |＋|b |，当且仅当ab ≥0时等号成立；定理2：如果a ，b ，c 是实数，那么|a －c |≤|a －b |＋|b －c |，当且仅当(a －b )(b －c )≥0时等号成立.绝对值三角不等式在解答含有绝对值的不等式、函数问题中应用广泛，下面结合实例,来谈一谈如何巧妙运用绝对值三角不等式解题.一、求解绝对值不等式问题绝对值不等式问题有很多种，如解绝对值不等式、证明绝对值不等式、求绝对值不等式中参数的取值范围.解答此类问题，通常需先将不等式进行合理的变形，然后根据绝对值三角不等式将不等式进行放缩，以便使不等式左右两边的式子成为同构式，再利用函数的单调性来解不等式，或将问题转化为函数最值问题，利用函数的性质、图象来解题.例1.若存在实数x 使|x －a |＋|x －1|≤3成立，则实数a 的取值范围是_____．解：∵|x －a |＋|x －1|≥|(x －a )－(x －1)|＝|a －1|，要使|x －a |＋|x －1|≤3有解，可使|a －1|≤3，∴－3≤a －1≤3，∴－2≤a ≤4.解答本题,主要利用了绝对值三角不等式.将问题转化为解绝对值不等式，通过解不等式，便可求得参数的取值范围.例2.已知二次函数f ()x =ax 2+bx +c 满足||f ()-1≤1，||f ()0≤2，||f ()1≤1，试证明：当||x ≤1时，不等式||f ()x ≤178成立.证明：由||f ()-1≤1，||f ()0≤2，||f ()1≤1，得ìíîïïf ()-1=a -b +c,f ()0=c,f ()1=a +b +c,即ìíîïïïïa =12f ()1-f ()0+12f ()-1，b =12f ()1-12f ()-1，c =f ()0，因此||f ()x =||ax 2+bx +c =|||éëùû12f ()1-f ()0+12f ()-1x 2|||+éëùû12f ()1-12f ()-1x +f ()0=|||12f ()1()x 2+x +f ()0()1-x 2|||+12f ()-1()x 2-x ≤12||f ()1|x 2+x +||f ()0|1-x 2+12·||f ()-1|x 2-x ≤12||x ||x +1+2||1-x 2+12||x ||x -1=12||x ·()x +1+2()1-x 2+12||x ()1-x =||x +2()1-x 2，当||x ≤1时，||x +2()1-x 2=||x +2()1-||x 2=-2·æèöø||x -142+178，其最大值为178，因此||f ()x ≤178.我们需先通过整体代换，用f ()-1、f ()1、f ()0来表示f ()x ，而||f ()x 中含有多个绝对值，为了证明不等式||f ()x ≤178，需巧妙利用绝对值三角不等式，将目标式进行放缩，从而去掉部分绝对值符号，将问题转化为求||x +2()1-||x 2的最值.二、解答含有绝对值的函数最值问题求解含有绝对值的函数最值问题，可巧用绝对值三角不等式，将含有绝对值的式子进行适当的放缩，使其简化，然后根据绝对值三角不等式取“=”的条件来寻找目标式取得最值时自变量的值.运用绝对值三角不等式，能使含有绝对值的函数最值问题变得简单，可省去许多对绝对值进行分类讨论的过程.例3.求函数y =||x +1+||x +2+…+||x +99的最小值.解：由绝对值三角不等式可得：||x +1+||x +99≥||()x +1-()x +99=98，当且仅当()x +1()x +99≤0时成立，即当-99≤x ≤-1时，“=”成立，因此，当-99≤x ≤-1时，()||x +1+||x +99min=98，当-98≤x ≤-2时，()||x +2+||x +98min =96，当-97≤x ≤-3时，()||x +3+||x +97min =94，⋯，当-51≤x ≤-49时，()||x +49+||x +51min =2，可得当x =-50时，y =||x +1+||x +2+…+||x +99=98+96+…+2+0=2450，即y =||x +1+||x +2+…+||x +99的最小值为2450.运用绝对值不等式求解含有绝对值的函数最值问题，需充分关注绝对值三角不等式：||a |－|b ||≤|a ±b |≤|a |＋|b |取“=”时的情况.总之，在解答含有绝对值的不等式、函数问题时，同学们要注意将问题与绝对值三角不等式关联起来，灵活运用绝对值三角不等式,将含有绝对值的式子进行放缩，使其简化，再根据绝对值不等式、函数的性质来解题.（作者单位：江苏省南通市海门证大中学）思路探寻45。

绝对值三角不等式课件

与其他数学知识的结合
绝对值三角不等式与函数
绝对值三角不等式可以应用于函数的性质和图像分析，例如判断函数的单调性、求函数的极值等。
绝对值三角不等式与数列
在数列的项间关系和求和问题中，绝对值三角不等式可以用来处理带有绝对值的项，简化计算过程。
在实际生活中的应用
交通规划
在交通路线的规划中，绝对值三角不等式可以用于计算最短路径，优化交通网络。
答案与解析
答案
$(1,0)$ 或 $(0,1)$ 或 $( - 1, - 1)$ 或 $(1, - 1)$
VS
解析
根据绝对值的性质，将不等式转化为 $2a = 2(a + 1)$，解得 $a = -1$，再代入原式得到 $(b, a) = (0, -1)$ 或 $(1, -1)$。
THANKS
在数列求和中的应用
总结词
绝对值三角不等式可以用于简化数列求和的过程，特别是对于一些项之间存在一定关系的数列。
详细描述
通过利用绝对值三角不等式，可以将数列中的绝对值项进行放缩，从而将数列求和问题转化为更容易处理的形式。
举例
例如，对于数列 { a_n }，其中 a_n = |a_(n-1) - a_(n-2)|，可以利用绝对值三角不等式得出其求和结果。
03
绝对值三角不等式的应用
在不等式证明中的应用
总结词
绝对值三角不等式是证明不等式的重要工具之一，它可以用于简
化不等式的证明过程。
详细描述
绝对值三角不等式可以用来证明一些复杂的不等式，通过将不等式中的绝对值项进行放缩，将其转化为更容易处理的形式，从而
简化证明过程。
举例
例如，要证明 |a+b| ≤ |a| + |b| ，可以利用绝对值三角不等式直

绝对值三角不等式课件

[例2] (1)求函数y＝|x－3|－|x＋1|的最大值和最小值． (2)设a∈R，函数f(x)＝ax2＋x－a(－1≤x≤1)．若|a|≤1，求|f(x)|的最大值． [思路点拨] 利用绝对值三角不等式或函数思想方法可求解．
[解] (1)法一：||x－3|－|x＋1|| ≤|(x－3)－(x＋1)|＝4， ∴－4≤|x－3|－|x＋1|≤4. ∴ymax＝4，ymin＝－4.
4．求函数f(x)＝|x－1|＋|x＋1|的最小值．解：∵|x－1|＋|x＋1|＝|1－x|＋|x＋1|≥ |1－x＋x＋1|＝2，当且仅当(1－x)(1＋x)≥0，即－1≤x≤1时取等号． ∴当－1≤x≤1时，函数f(x)＝|x－1|＋|x＋1| 取得最小值2.
5．若对任意实数，不等式|x＋1|－|x－2|>a恒成立，求a的取值范围．解：a<|x＋1|－|x－2|对任意实数恒成立， ∴a<[|x＋1|－|x－2|]min. ∵||x＋1|－|x－2||≤|(x＋1)－(x－2)|＝3， ∴－3≤|x＋1|－|x－2|≤3. ∴[|x＋1|－|x－2|]min＝－3. ∴a<－3.即a的取值范围为(－∞，－3)．
绝对值三角不等式
绝对值三角不等式 (1)定理1：如果a，b是实数，则|a＋b|≤|a|＋|b|，当且仅当 ab≥0 时，等号成立．几何解释：用向量a，b分别替换a，b. ①当a与b不共线时，有|a＋b|<|a|＋|b|，其几何意义为：三角形的两边之和大于第三边． ②若a，b共线，当a与b 同向时，|a＋b|＝|a|＋|b|，当a与b 反向时，|a＋b|<|a|＋|b|. 由于定理1与三角形之间的这种联系，故称此不等式为绝对值三角不等式． ③定理1的推广：如果a，b是实数，则||a|－|b||≤|a±b| ≤|a|＋|b|.

绝对值三角不等式课件

题中也有着重要的应用。例如，在求函数的最小值或最大值时，可以利用绝对值三角不等式对函数进行放缩，从而得到函数的最值。
在应用绝对值三角不等式求函数最值时，需要注意处理函数定义域内的特殊情况，以及根据函数的性质选择合适的放缩方法。
在数列求和中的应用
总结词
绝对值总是非负的，即对于任何实数x，都有|x| ≥ 0。
详细描述
绝对值表示一个数值不考虑正负的大小，因此无论x是正数、负数还是零，其绝对值都是非负的。这是绝对值的基本性质之一，也是理解绝对值三角不等式的基础。
绝对值的传递性
总结词
如果a ≥ b且b ≥ c，那么a ≥ c。
详细描述
绝对值的传递性是指，如果一个数a大于或等于另一个数b，而这个数b又大于或等于数c，那么这个数a必然大于或等于数c。这个性质在数学中非常重要，也是绝对值三角不等式推导的基础。
绝对值三角不等式在数列求和问题中也有着重要的应用。例如，在求解数列的项的和或前n项和时，可以利用绝对值三角不等式对数列进行放缩，从而得到数列的和的上下界。
在应用绝对值三角不等式求数列和时，需要注意处理数列的项的正负交替出现的情况，以及根据数列的性质选择合适的放缩方法。
05
绝对值三角不等式的变式
绝对值三角不等式的几何意义
几何解释
绝对值三角不等式表示在数轴上任意两点A和B的距离之和，等于它们到原点O的距离之和，即 |OA|+|OB|=|AB|。
应用举例
在解决实际问题时，如测量、定位、计算距离等问题，可以利用绝对值三角不等式来求解。
02
绝对值三角不等式的性质
Chapter
绝对值的非负性
绝对值的可加性
总结词
对于任意实数a和b，有|a + b| ≤ |a| + |b|。

人教B版高中数学选修4-5课件：1.4绝对值的三角不等式

A.|a|<|b|+|c|B.|c|<|a|+|b|
C.b>||c|-|a||D.b<|a|-|c|
解析:由|a-c|<b,可知b>0,∴b=|b|. ∵|a|-|c|≤|a-c|, ∴|a|-|c|<b,则|a|<b+|c|=|b|+|c|,
故选项A成立. 同理,由|c|-|a|≤|a-c|,得|c|-|a|<b,
8
目标导航
Z Z 知识梳理 HISHISHULI
重难聚焦
HONGNANJUJIAO
D S 典例透析 IANLITOUXI
随堂演练
UITANGLIANXI
题型一题型二题型三
利用绝对值不等式证明不等式
【例1】设m等于|a|,|b|和1中最大的一个,当|x|>m时,求证
:
��
+
10
目标导航
Z Z 知识梳理 HISHISHULI
重难聚焦
HONGNANJUJIAO
D S 典例透析 IANLITOUXI
随堂演练
UITANGLIANXI
题型一题型二题型三
利用绝对值的三角不等式求函数的最值
【例2】求函数y=|x-3|-|x+1|的最大值和最小值.
分析:若把x-3,x+1看作两个实数,则所给的代数式符合两个数绝
Z Z 知识梳理 HISHISHULI
重难聚焦
HONGNANJUJIAO
D S 典例透析 IANLITOUXI
随堂演练
UITANGLIANXI
12345
2已知h>0,a,b∈R,命题甲:|a-b|<2h;命题乙:|a-1|<h,且|b-1|<h,则甲是乙的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分又不必要条件解析:显然a与b的距离可以很近,满足|a-b|<2h,但此时a,b与1的距离可以很大,因此甲不能推出乙.另一方面,若|a-1|<h,|b-1|<h,则|ab|=|a-1+1-b|≤|a-1|+|b-1|<2h,即乙可以推出甲. 因此甲是乙的必要不充分条件. 答案:B

5.2绝对值三角不等式课件(人教A版选修4-5)

a<0,b<0 a+b x a O b |a+b|=|a|+|b|
x
a<0,b>0 a+b x a O b |a+b|<|a|+|b|
易得: |a+b|=|a|+|b|
(3)如果ab=0,则a=0或b=0
综上所述,可得:
定理1: 如果a,b是实数,则 |a+b||a|+|b| 当且仅当ab0时,等号成立. 如果把定理1中的实数a,b分别换为向量
同学们能再探究一下|a|-|b|与|a+b|, |a|+|b|与 |a-b|, |a|-|b|与|a-b|等之间的关系? 如: 如果a,b是实数,则 |a|-|b||a-b||a|+|b| 再如: 如果a,b,c是实数,则 |a-c||a-b|+|b-c|
当且仅当(a-b)(b-c)0时,等号成立.
类比不等式基本性质的得出过程，同学们认为
可以怎样提出关于绝对值不等式性质的猜想？
从“运算”的角度考察绝对值不等式。如：对于实数a,b，可以考察|a|, |b|, |a+b|, |a-b|, |a|+|b|, |a|-|b| 等之间的关系。
用恰当的方法在数轴上把|a|, |b|, |a+b|表示出来，
S(x)=2(|x-10|+|x-20|) |x-10|+|x-20|=|x-10|+|20-x| |(x-10)+(20-x)|=10 当且仅当(x-10)(20-x)0时取等号. 又解不等式:
S 60 40 20
S(x)=2(|x-10|+|x-20|)

高中数学人教A版选修课件：1.2.1 绝对值三角不等式

二
绝对值不等式
-1-
1.绝对值三角不等式
-2-
1.理解绝对值的几何意义.
2.掌握绝对值三角不等式及其几何意义.
3.掌握三个实数的绝对值不等式及应用.
1.对绝对值三角不等式的理解
剖析:绝对值三角不等式实质是两个实数的和差的绝对值与绝对
值的和差的关系,我们可以类比得到另外一种形式:|a|-|b|≤|ab|≤|a|+|b|.
∴|c|<|a|+b=|a|+|b|.故B成立.
而由A成立,得|c|-|a|>-|b|,
由B成立,得|c|-|a|<|b|,
∴-|b|<|c|-|a|<|b|.
即||c|-|a||<|b|=b.故C成立.
由A成立知D不成立.故选D.
答案:D
题型一
题型二
题型二
题型三
用绝对值三角不等式的性质证明不等式
a,b不共线时,a+b,a,b构成三角形,有|a+b|<|a|+|b|.当向量a,b共线时,
若a,b同向(相当于ab≥0)时,则|a+b|=|a|+|b|;若a,b异向(相当于ab<0)
时,则|a+b|<|a|+|b|,这些都是利用了三角形的性质定理,如两边之和
大于第三边等,这样处理,可以形象地描绘绝对值三角不等式,更易
|+|
证明不等式:
1+|+|
≤
||
||
+
.
1+|| 1+||
证明:当 a+b=0 时,不等式显然成立.
当 a+b≠0 时,∵|a+b|≤|a|+|b|,

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

课题：绝对值三角不等式
红岭中学隗双和
教学目标：
知识与技能：了解绝对值三角不等式的含义，理解绝对值三角不等式公式及推导方法，会
进行简单的应用。

过程与方法：充分运用观察、类比、猜想、分析证明的数学思维方法，体会转化和数形结合
的数学思想，并能运用绝对值三角不等式公式进行推理和证明。

情感、态度与价值观：体验不等式的美感，提高推理能力，增强学习兴趣。

能运用所学的知
识，正确地解决的实际问题.
教学重点：绝对值三角不等式的含义，绝对值三角不等式的理解和运用。

教学难点：绝对值三角不等式的发现和推导、取等条件。

授课类型：新授课课时安排：1课时
教具：多媒体辅助。

教学过程：
一、复习引入：
关于含有绝对值的不等式的问题，主要包括两类：一类是解不等式，另一类是证明不等式。

本节课探讨不等式证明这类问题。

1．请同学们回忆一下绝对值的意义。

⎪⎩
⎪
⎨⎧<-=
>=0000x x x x x x ，如果，如果，如果。

几何意义：在数轴上，一个点到原点的距离称为这个点所表示的数的绝对值。

即
2．证明一个含有绝对值的不等式成立，除了要应用一般不等式的基本性质之外，经常还要用到关于绝对值的和、差、积、商的性质：
（1）a a ≥，当且仅当0≥a 时等号成立，.a a -≥当且仅当0≤a 时等号成立。

（2）2
a a =，（3）
b a b a ⋅=⋅，（4）
)0(≠=
b b
a
b
a 那么?
b a b a +=+?b a b a +=-
二、讲解新课：
结论：a b a b ++≤（当且仅当0ab ≥时，等号成立.）
已知,a b 是实数，试证明：a b a b ++≤（当且仅当0ab ≥时，等号成立.）
探究: ,,a b a b +, 之间的什么关系?
b a -
a
r b
r a b
+r r 方法一：证明:10 .当ab ≥0时, 20
. 当ab <0时,
综合10,20知定理成立.
方法二：分析法，两边平方（略）
定理1 如果,a b 是实数，则a b a b ++≤（当且仅当0ab ≥时，等号成立.）
（1）若把,a b 换为向量,a b r r
情形又怎样呢？
（2）若把,a b 换为复数12,z z ，结论：1212z z z z ++≤成立吗？
根据定理1，有b b a b b a -+≥-++，就是，a b b a ≥++。

所以，b a b a -≥+。

定理（绝对值三角形不等式）
如果,a b 是实数，则a b a b a b -±+≤≤ 注：当a b 、为复数或向量时结论也成立. 推论1
1212n n a a a a a a ++++++L L ≤
推论2：如果a b c 、、是实数,那么a c a b b c --+-≤,当且仅当()()0a b b c --≥时,等号成立.
思考：如何利用数轴给出推论2的几何解释？
（设A ，B ，C 为数轴上的3个点，分别表示数a ，b ，c ，则线段.CB AC AB +≤当且仅当C 在A ，B 之间时，等号成立。

这就是上面的例3。

特别的，取c ＝0（即C 为原点），就得到例2的后半部分。

）三、典型例题：
a r b
r ||,
||||||=+=====+ab ab a b a
b ||,||||||
=-+===<==+ab ab a b a b a b
+r r
例1、已知 2
,2c
b y
c a x <-<
-，求证 .)()(c b a y x <+-+ 证明 )()()()(b y a x b a y x -+-=+-+ b y a x -+-≤ （1）
2
,2c b y c a x <-<
-Θ， ∴c c
c b y a x =+<-+-2
2 （2）
由（1），（2）得：c b a y x <+-+)()(
例2、已知.6,4a
y a x <<
求证：a y x <-32。

证明 6,4a y a x <<Θ，∴2
3,22a
y a x <<，
由例1及上式，a a
a y x y x =+<+≤-2
23232。

注意：在推理比较简单时，我们常常将几个不等式连在一起写。

但这种写法，只能用于不等号方向相同的不等式。

例3 两个施工队分别被安排在公路沿线的两个地点施工,这两个地点分别位于公路路碑的第10公里和第20公里处.现要在公路沿线建两个施工队的共同临时生活区,每个施工队每天在生活区和施工地点之间往返一次,要使两个施工队每天往返的路程之和最小,生活区应该建于何处?
解：如果生活区建于公路路碑的第 x km 处，两施工队每天往返的路程之和为S(x)km 那么 S(x)=2(|x-10|+|x-20|)
四、课堂练习：
1.(课本20P 习题1.2第1题)求证:
⑴2a b a b a ++-≥;⑵2a b a b b +--≤ 2. (课本20P 习题1.2第3题)求证:
⑴x a x b a b -+--≥;⑵x a x b a b ----≤ 3．（1）、已知.2,2c
b B
c a A <-<
-求证：c b a B A <---)()(。

（2）、已知.6
,4c
b y
c a x <-<-求证：c b a y x <+--3232。

五、课堂小结：
1．实数a 的绝对值的意义:
·10
x
··20
⑴(0)0(0)(0)a a a a a a >⎧⎪
==⎨⎪-<⎩
;（定义）
⑵a 的几何意义:
2．定理（绝对值三角形不等式）
如果,a b 是实数，则a b a b a b -±+≤≤注意取等的条件。

六、课外作业：1。

必做：课本19第2，4，5。

2．选作：（1）．求证
.111b
b a
a b
a b a ++
+≤
+++
（2）．已知 .1,1<<b a 求证：
.11<++ab
b
a
七．教学反思：
绝对值三角不等式结构优美，构思巧妙，他的发现、证明、应用能够培养学生的探索、发现、推理能力，有着良好的培养学生能力的机会，因此本节课之前应该给学生安排课外预习、自学绝对值三角不等式的含义、意义、证明等重要内容，以让学生对绝对值三角不等式有初步的了解，本节课上可以放手让学生探索绝对值三角不等式的发现、意义和特点、证明的方法、应用的结构特点等问题，使课堂内容更加丰富，学生思维活动更加主动、激烈，另外在探究过程中，学生个体的差异比较明显，对于部分反应较慢的学生，要加强及时课堂的个别指导，从而更加体现新课程的要求，全面锻炼学生的能力。

课题绝对值三角不等式

合集下载