- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1:已知 >0 |x-a|< |y-b|< , 求证:|2x+3y-2a-3b|<5 .
证明: |2x+3y-2a-3b| =|(2x-2a)+(3y-3b)|
|2(x-a)|+|3(y- b)| =2|x-a|+3|y-b| <2 +3 =5 故 |2x+3y-2a-3b|<5
例2 已知 x a , 0 y b , y 0, M ,
当且仅当(a-b)(b-c) 0时,等号成立.
定理2的几何意义
在数轴上,a,b,c所对应的点分别为A,B,C,
AB C x a• b• c•
A
CB x
• •a
•c
•
b
B
AC x
b• •
a• •c
(1)当点B在点A,C之时, |a-c|=|a-b|+|b-c|
(2)当点B在点A,C之外时, |a-c|<|a-b|+|b-c|
2M
2a
求证:xy ab .
证明:xy ab xy ya ya ab yx a ay b
y x a a y b M a . 2M 2 a
1.①已知
x
r
0, a 0,求证
1 ax
1 ar
.
②已知 an l 1, 求证 an l 1 .
2.已知 A a , B b ,
2
2
求证:① A B a b ;
② A Ba b .
例3.已知 | a | 1, | b | 1, 求证 a b 1 1 ab
证明:a b 1 ab
1
(a b)2 (1 ab)2
1
a2 2ab b2 1 2ab a2b2
1 a2 b2 a2b2 0
(1 a2 )(1 b2 ) 0
绝对值的几何意义
a, a 0 |a|= 0, a 0
a, a 0
|a| A
O
a
x
几何意义:
表示数轴上坐标为a的点A到原点的距 离.
a b, a b
A |a-b| B
|a-b|= 0, a b
a 几何意义:
b
x
b a, a b 表示数轴上实数a,b对应的点A,B之
间的距离,即线段AB的长度
同学们能再探究一下|a|-|b|与|a+b|, |a|+|b|与 |a-b|, |a|-|b|与|a-b|等之间的关系?
如:如果a,b是实数,则 |a|-|b| |a-b| |a|+|b|
再如:如果a,b,c是实数,则 |a-c| |a-b|+|b-c|
当且仅当(a-b)(b-c) 0时,等号成立.
当ab<0时,ab=-|ab|,
|a+b| a b2 a2 2ab b2
| a |2 2 | ab | | b |2
a2 2 | ab | b2
| a |2 2 | ab | | b |2 | a | | b |2
| a | | b |
故
当且仅当ab 0时,等号成立.
|a+b| |a|+|b|,
类比不等式基本性质的得出过程,同学们认为可以 怎样提出关于绝对值不等式性质的猜想?
从“运算”的角度考察绝对值不等式。
如:对于实数a,b,可以考察|a|, |b|, |a+b|, |a-b|, |a|+|b|, |a|-|b| 等之间的关系。
用恰当的方法在数轴上把|a|, |b|, |a+b|表示出 来,同学们观察能发现它们之间有什么关系?
a+b b• •
•
O
•a
x
|a+b|<|a|+|b|
a<0,b>0
•a
•
O
a+b • b•
x
|a+b|<|a|+|b|
(3)如果ab=0,则a=0或b=0 易得: |a+b|=|a|+|b|
综上所述,可得:
定理1: 如果a,b是实数, 则 |a+b| |a|+|b|, 当且仅当ab 0时,等号成立.
ab>0
• • • a•+b x Oa b
a+•b • b
•a
•
O
x
a+b b• •
ab<0
•
O
•a
x
•a
•
O
a+b • b•
x
(1)当ab>0时, a>0,b>0
a<0,b<0
• • • a•+b Oa b
由图可得:
x
a+•b •
b
|a+b|=|a|+|b|
•a
•
O
x
(2)当ab<0时 a>0,b<0
由 | a | 1, | b | 1,可知 (1 a2 )(1 b2 ) 0成立,
所以 a b 1 1 ab
ab
a
b
例4
求证1
ab
1
a
1
b
.
证明:在 a b 0 时,显然成立.
当 a b 0 时,左边
1 1 1
ab
1 1
ab 1 1 a b
2.1绝对值三角不等式
本节课从复习绝对值的代数意义和几何意义导入,引入 绝对值三角不等式,在讲述绝对值三角不等式的过程中, 采用边探究边论证的方式,让学生在形成过程中理解并记 忆绝对值三角不等式。再借助例题加以巩固,例题的选取 具有层次性,尤其到最后的例题具有一定的难度。
在理解绝对值三角不等式的过程中,即从几何意义理解 公式,也从代数角度论证公式,绝对值是高中阶段的一个 重要概念,绝对值三角不等式也非常重要,所以在讲解的 过程中重点是理解公式并通过例题巩固。通过例题和练习 题注意式子的变形和等号的成立条件,在例题中还补充了 思考题让学生分析如何处理含有绝对值的问题
|a+b|<|a|+|b|
当向量a b 共线呢?
故该定理的几何意义为:
三角形的两边之和大于第三边.
绝对值三角不等式: |a+b| |a|+|b| 证明: 当ab 0时,ab=|ab|
|a+b| a b2 a2 2ab b2
a |2 2 | ab | | b |2
| a | | b |2 a b
定理2: 如果a,b,c是实数,则 |a-c| |a-b|+|b-c|
当且仅当(a-b)(b-c) 0时,等号成立. 分析:由于a-c, a-b与b-c都是实数,且 a-c=(a-b)+(b-c) 则可使用定理1的结论进行证明. 证明:根据定理1,有:
|a-c|=|(a-b)+(b-c)| |a-b|+|b-c|
如果把定理1中的实数a,b分别换为向量 a, b,能得
出什么结果?
定理1的几何意义
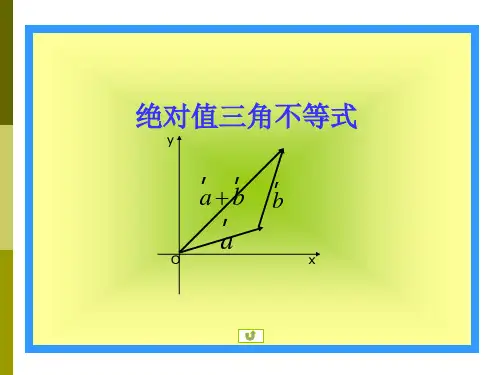
在不等式|a+b| |a|+|b|中, 绝对值三角不等式
用向量 a、b 分别替换实数a,b,
y
a b 当向量 a b 不共线时,则由向量加法的
三角形法则,
b
向量 a、b、a+b 构成三角形,
ax
O
故可得向量形式的不等式: