- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
xfX (x)dx yfY ( y)dy E(X ) E(Y )
上页 下页 返回
4. 若X与Y独立,则E(XY)=E(X)E(Y).
证明:设(X,Y)~f(x,y)
E(XY ) xyf (x, y)dxdy
xyfX (x) fY ( y)dxdy
度函数为f(x),
-<x<,
若
|
x|
f
( x)dx收敛
则称
E(X) xf (x)dx .
为随机变量X的数学期望。
上页 下页 返回
例4. 若随机变量X服从拉普拉斯分布,其密度函数为
f (x)
1
2
exp
x
试求E(X).
解
x x
k 1
k 1
X的数学期望,记为E( X )
上页 下页 返回
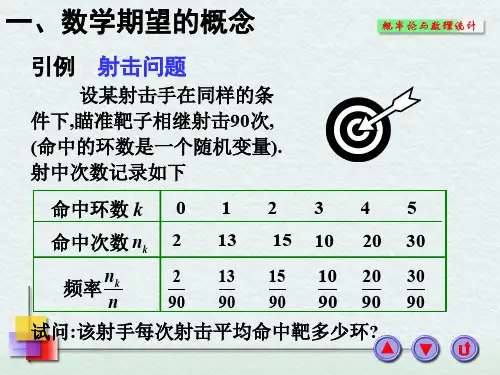
例2 掷一颗均匀的骰子,以X表示掷得的点数,求X 的数学期望。
E( X ) 6 k 1 7
k 1 6 2
例3 某厂生产的产品中,25%是一等品,50 %是二等品, 15 %是三等品,10 %是次品。如果每件一,二,三等品分 别获利5、4、3元,一件次品亏损2元,试问该厂可以期望每 件产品获利多少元?
上页 下页 返回
例7 长途汽车起点站于每时的10分、30分、55分 发车,设乘客不知发车时间,于每小时的任意时
刻随机地到达车站,求乘客的平均候车时间
0 10
30
55 60
解:设乘客于某时X分到达车站,候车时间为Y,则
10 X
Y
g(X )
30 55
X X
0 X 10 10 X 30 30 X 55
i 1
n
n
E(X ) E(Xi ) p np
i 1
i 1
上页 下页 返回
例11 若有n把看上去样子相同的钥匙,其中,只有 一把能打开门上的锁,用它们去试开门上的锁。设 取到每把钥匙是等可能的,每把钥匙试开一次后除 去。试用下面两种方法取求试开次数X的数学期望。
(1)写出X的分布律;(2)不写出X的分布律;
i}
1 n
,
E{X
i
i}
i, n
所以
E(X )
E
n i1
Xi
n i1
E(Xi )
1 (1 n
2 ... n)
n 1 2
j 1
10[0.99100 (101)(1 0.99100 )] 1000[1 1 0.99100 ]
100
644
上页 下页 返回
例10 若X~B(n,p),求E(X)
解:设
1 第i次试验事件A发生
Xi 0 第i次试验事件A不发生
则
n
E(Xi) p
X Xi
2
3
x2
x2
e 2 dx
2
3
上页 下页 返回
4.1.3.数学期望的性质
1. E(c)=c,c为常数; 2。E(cX)=cE(X), c为常数; 证明:设X~f(x),则
E(cX ) cxf (x)dx
c xf (x)dx cE(X )
上页 下页 返回
3. E(X+Y)=E(X)+E(Y);
证明:设(X,Y)~f(x,y)
E(X Y ) (x y) f (x, y)dxdy
xf (x, y)dxdy yf (x, y)dxdy
x[ f (x, y)dy]dx y[ f (x, y)dx]dy
解
(1)P{X
k}
Pk 1 n1
1,k
1, 2,...n.
Pnk n
E( X ) n kP{X k} 1 n k n 1
k 1
n k 1
2
精品课件!
精品课件!
(2)令Xi
i 0
第i把钥匙打开锁 其他
n
则X Xi
i 1
而
P{X i
E(X 2)
x2
x2
e 2 dx
2
1
x2
e 2 dx 1
2
x
x2
de 2
2
上页 下页 返回
E(X 3)
x3
x2
e 2 dx 0
2
E(X 4)
x4
x2
e 2 dx
2
x3
x2
de 2
解: Y 1 0
Pk
2 3
1 3
E(Y ) 1 2 0 1 2 3 33
上页 下页 返回
定理1 设X是离散型随机变量,它的分布律
P{X=xk}=pk, k=1,2,…, 则Y=g(X)(g是连续实函
数),若 g(xk)pk绝对收敛, 则Y的期望E(g(X))
为
E(Y ) E[g( X )] g(xk )pk . k 1
解:设Xj为第j组的化验次数, j 1,...10
X为1000人的化验次数,则
Xj 1 Pj (99%)100
101
1 (99%)100
上页 下页 返回
EX j 0.99100 (101)(1 0.99100)
10
10
E(X ) E( X j ) E(X j )
j 1
E(
X
)
2
exp
dx
令t x
t exp | t |dt
exp tdt
2
0
上页 下页 返回
4.1.2.随机变量函数的期望
例5:设随机变量X的分布律为
X -1 0 1
Pk
1 3
1 3
1 3
求随机变量Y=X2的数学期望
推论: 设(X, Y)是二维离散型随机变量,它们的
联合分布律为 P{X=xi ,Y=yj,}= pij, i, j=1, 2, … ,
则Z= g(X,Y)的期望
E(Z ) E[g( X ,Y )]
g (xi , y j )pij .
j 1 i1
上页 下页 返回
例6 设随机变量(X,Y)的分布律如下,求E(XY)
x y1 2
0
0.15 0.15
1
0.45 0.25
解: E(XY) 010.15 020.15 110.45 120.25
0.95
上页 下页 返回
定理2 设X是连续型随机变量,它的概率 密度为f(x), Y=g(X) (g是连续实函数),若
g(x) f (x)dx 绝对收敛,则Y=g(X)的期望 E(Y) E[g(X)] g(x)f (x)dx .
xfX (x)dx yfY ( y)dy E(X )E(Y )
上页 下页 返回
例9.设某种疾病的发病率为1%,在1000个人中普查 这种疾病,为此要化验每个人的血。方法是,每100 个人一组,把从100个人抽来的血混在一起化验, 如果混合血样呈阴性,则通过,如果混合血样呈阳 性,则再分别化验该组每个人的血样。求平均化验 次数
解 设X表示每件产品的利润,显然它是一个离散型随机变 量,其分布律为
X -2 3 4 5
pi 0.1 0.15 0.5 0.25 上页 下页 返回
所以 E(X)=(-2)x0.1+3x0.15+4x0.5+5x0.25=3.5
即每生产一件产品平均获利3.5元。
定义 4.2 设X是连续型随机变量,其概率密
1 6 9 15 7 2
上页 下页 返回
40 1 60 6 70 9 80 15 90 7 100 2
40 40 40 40 40
40
76.5(分)
定义4.1 设X是离散型随机变量,它的分布
律是:
P(X=xk)=pk , k=1,2,…
如果级数 xk pk绝对收敛,则称级数 xk pk为
f
X
(
x)
1 60
0
70 X 55 X 60
1 60
E(Y ) 60 0 g(x)dx =10分25秒
0 x 60 others
上页 下页 返回
例8 设X服从N(0,1)分布,求E(X2),E(X3),E(X4)
f (x)
1
x2
e2
2
推论 设(X, Y)是二维连续型随机变量,它的概率
密度为f (x, y), Z=g(X, Y) (g是连续实函数)
g(x, y) f (x, y)dxdy绝对收敛,则Z=g(X, Y)的
期望
E(Z ) E[g( X ,Y )]
ቤተ መጻሕፍቲ ባይዱ
g(x, y) f (x, y)dxdy.
一.数学期望的定义
数学期望——描述随机变量取值的平均特征
例1 设某班40名学生的概率统计成绩及得分 人数如下表所示: